• Visualising multivariate continuous data using:
    • pairs to produce a scatterplot matrix
    • parallelplot package to produce a parallel coordinate plot
  • Introduce plots useful (and potentially not so useful) for getting an overview of a large data set
    • Correlation plots as a summary of a scatterplot matrix
    • Using heatmaps, glyphs, or faces to visualise and compare the cases in the data

You will need to install the following packages for today’s workshop:

  • lattice for the parallelplot function
install.packages("lattice")

1 Multivariate continuous data

1.1 Scatterplot matrices

Scatterplot matrices (sometimes inelegantly called “sploms”) are tables of scatterplots with each variable plotted against all others. They give excellent overviews of the relationships between many variables at once, and allow us to identify - by eye - any striking patterns of behavior between pairs of variables. In particular, if we’re interested in building a model for one particular variable then drawing a scatterplot matrix gives us a quick way of identifying which other variables in the data set are associated with in (and hence potentially useful predictors in a model), and which are not (and can likely be ignored).

Download data: marks

This data set (from the very end of Workshop 2) contains the exam marks of 88 students taking an exam on five different topics in mathematics. The data contain the separate marks for each topic on a scale of 0-100:

  • MECH - mechanics
  • VECT - vectors
  • ALG - algebra
  • ANL - analysis
  • STAT - statistics

As the data are all numeric, we can immediately draw a scatterplot matrix which will be a 5x5 grid of plots:

pairs(marks,pch=16)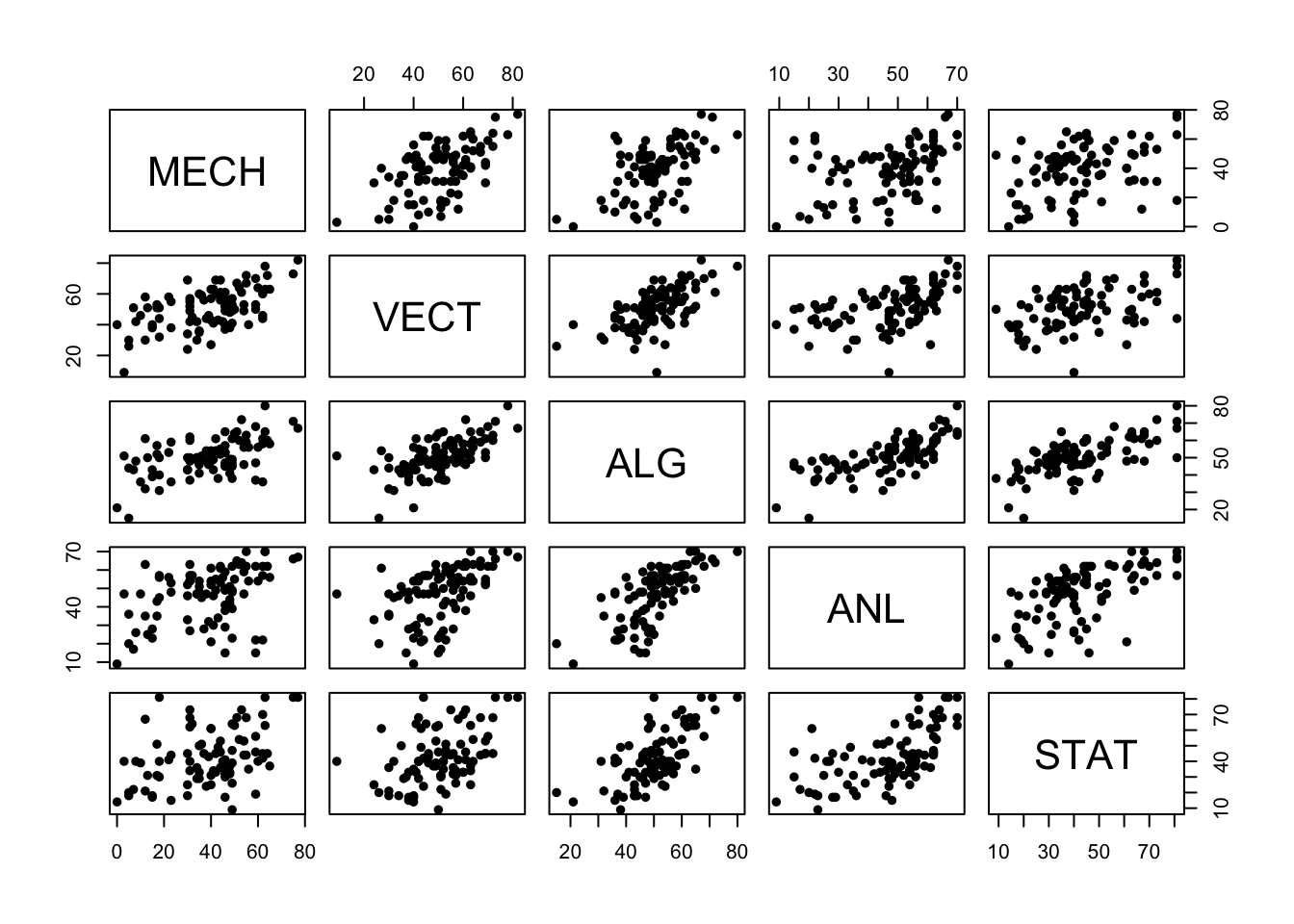

There are a number of things we can observe:

  • Almost all of these variables have a positive association, though some are stronger than others. High (low) performance on one subject seems to be connected with high (low) performance on other subjects.
  • The strongest association looks to be between Algebra and Analysis - two sub-disciplines of pure maths.
  • Statistics and Mechanics look to have the weakest association - Statistics and Theoretical Physics are conceptually very different
  • There are some very low and very high marks, including a single very low mark on VECT

As the relationships are reasonably linear, the correlation will give us a numerical summary of the strength of the relationships

cor(marks)
##           MECH      VECT       ALG       ANL      STAT
## MECH 1.0000000 0.5534052 0.5467511 0.4093920 0.3890993
## VECT 0.5534052 1.0000000 0.6096447 0.4850813 0.4364487
## ALG  0.5467511 0.6096447 1.0000000 0.7108059 0.6647357
## ANL  0.4093920 0.4850813 0.7108059 1.0000000 0.6071743
## STAT 0.3890993 0.4364487 0.6647357 0.6071743 1.0000000

Let’s use colour to identify this low mark (and possible outlier) to see where it falls within the distribution of the other marks:

library(scales)
colours <- rep('black',length=nrow(marks)) ## create a vector of same length as the data, by repeating "black"
colours <- alpha(colours,0.4) ## use some transparency to fade most of the cases
which(marks$VECT<10)     ##  find out which row in the data set has a VECT mark below 10
## [1] 81
colours[which(marks$VECT<10)] <- 'red' ## replace the colour for that row with "red"
pairs(marks,col=colours,pch=16)    ## now draw the plot using our custom colours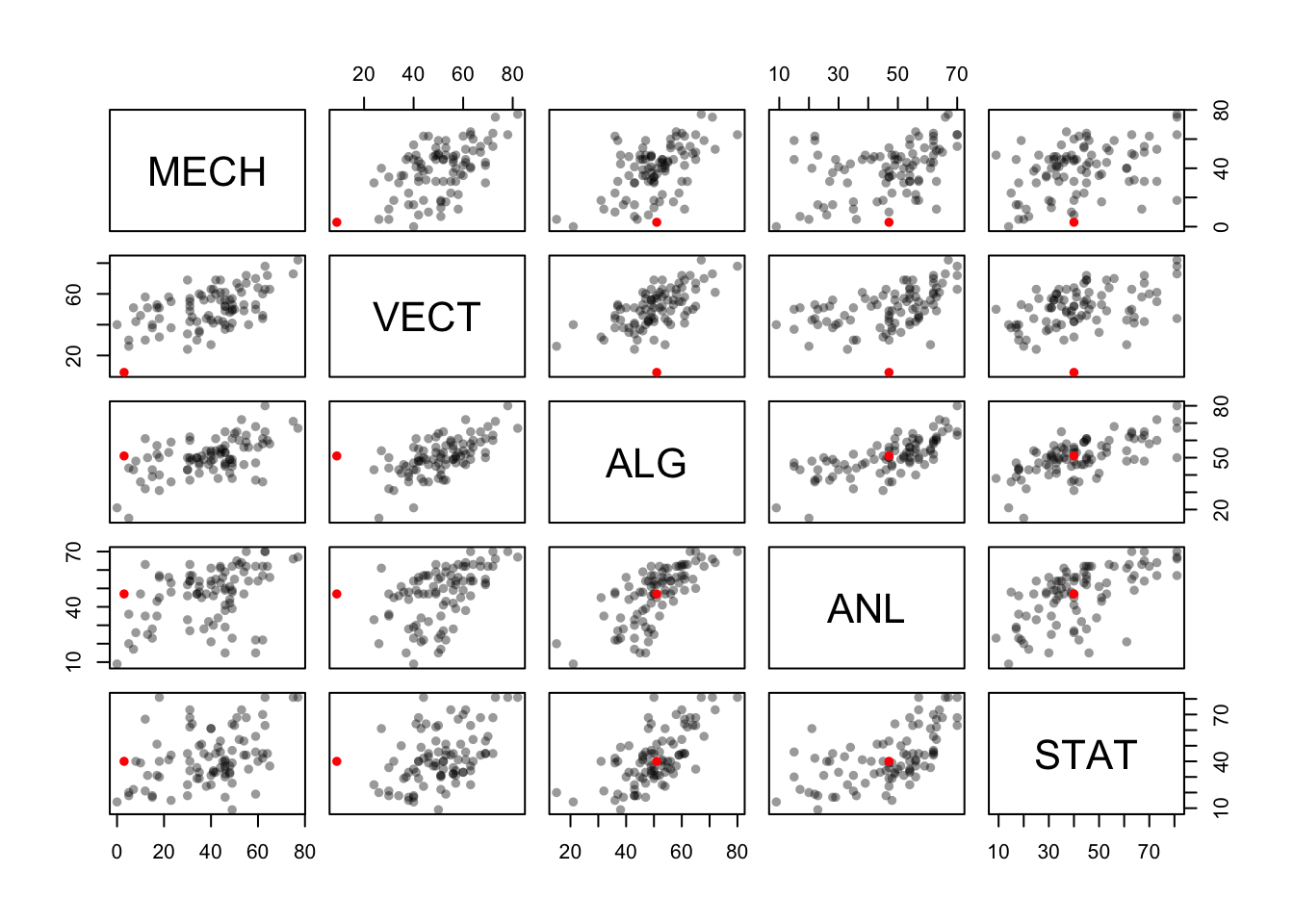

We find that this student did reasonably well on the other exams, but really didn’t do well with Mechanics or Vectors! These two topics are quite closely related, so this seems quite a natural outcome.

1.2 Parallel coordinate plot

We can also try a parallel coordinate plot (PCP). Parallel coordinates can be quite effective for showing multiple variables, and among the most common subjects of academic papers in visualization. While initially confusing, they are a very powerful tool for understanding multi-dimensional numerical datasets. To understand how the plot is produced, let’s look at a portion of the data:

MECH VECT ALG ANL STAT
77 82 67 67 81
63 78 80 70 81
75 73 71 66 81
55 72 63 70 68
63 63 65 70 63
53 61 72 64 73

Imagine each of these columns being mapped onto a vertical axis. Each data value would end up somewhere along the line, scaled to lie between the minimum at the bottom and the maximum at the top. A pure collection of points would not be terribly useful, however, so the points belonging to the same data point (row) are connected with lines. Drawing the plot for these few observations gives us:

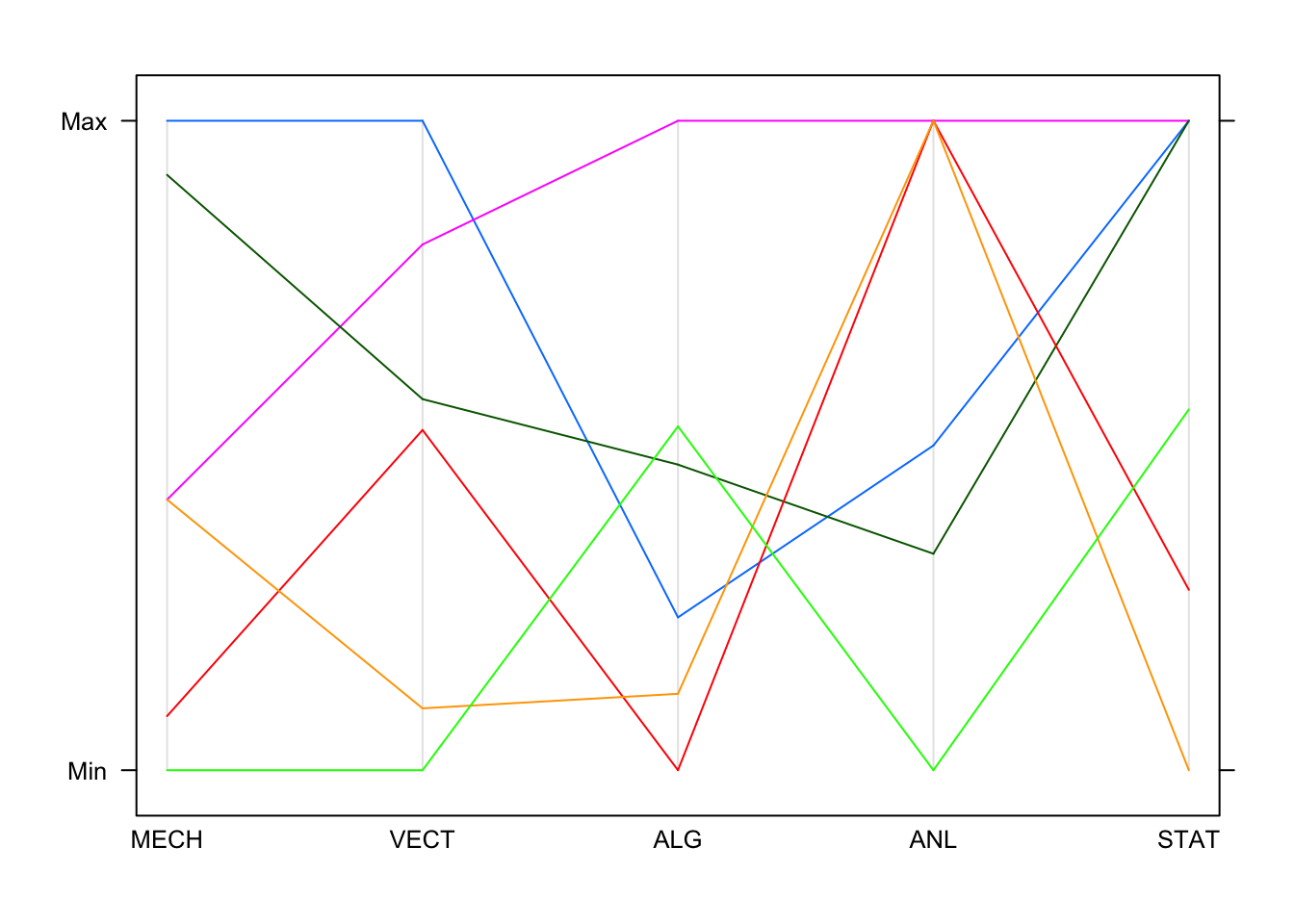
By default, each line is drawn in a different colour. This is fine for a small number of cases, but becomes messy with a lot of data - in this case it is best to override the colouring. You can also make the lines fatter by increasing the line width, e.g. add the lwd=2 argument to the plot command.

Now, if we draw all of the data we create the characteristic jumble of lines parallel coordinates are famous for. Colouring in the same was as we did the scatterplot, we get this:

library(lattice)
parallelplot(marks,horizontal=FALSE,col=colours)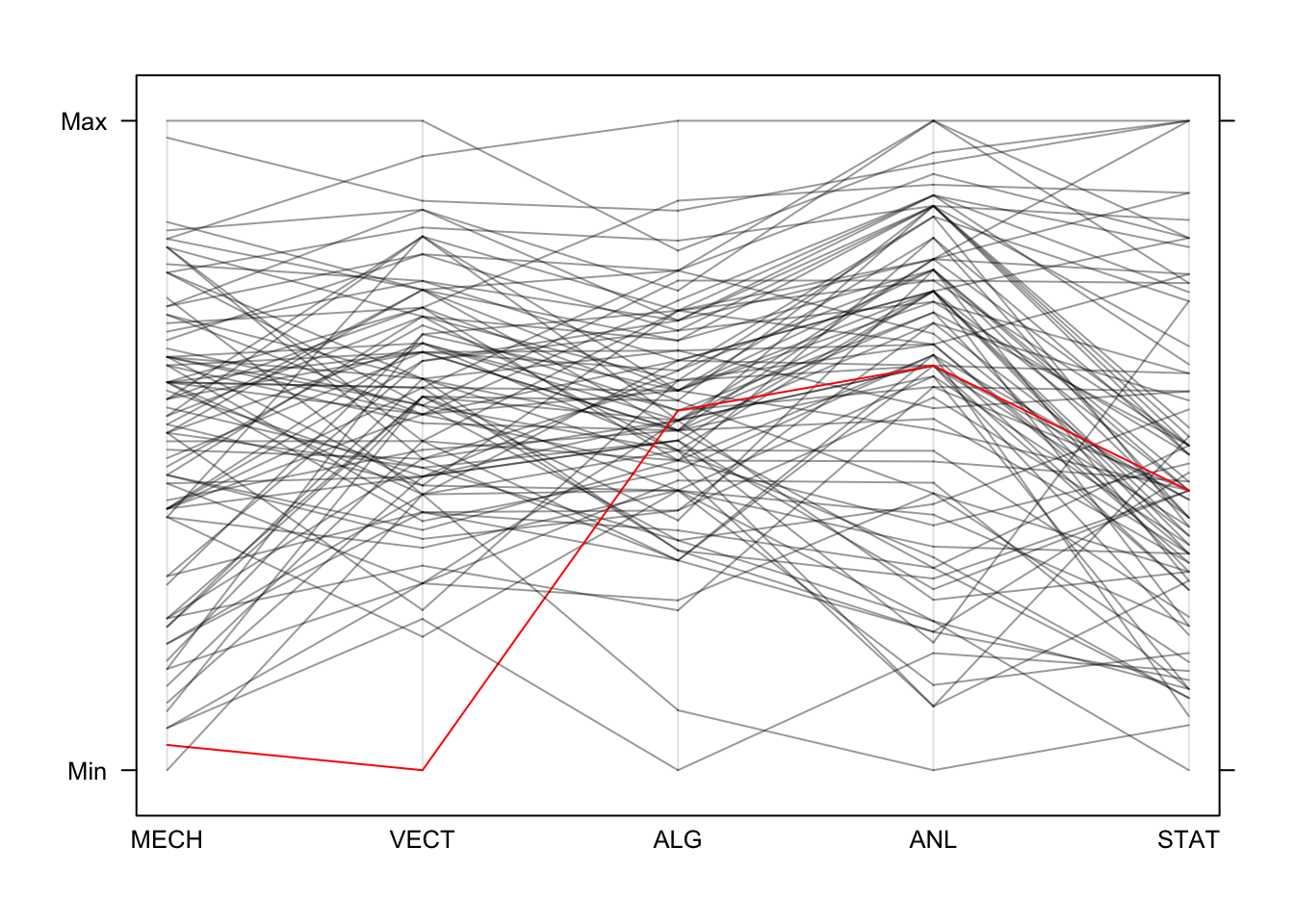

We can easily trace the red line’s performance across the different exams. When there are bigger groups defined in the data, we can get the parallelplot function to colour the groups automatically by passing the grouping variable into the groups argument. Unfortunately, we don’t have a group variable here but we can make one to illustrate the technique. We could have equally created a group variable to identify and highlight our outlier above.

## make a categorical variable to separate high scores on STATistics
hiStat <- factor(marks$STAT<70) 
parallelplot(marks,horizontal=FALSE,groups=hiStat)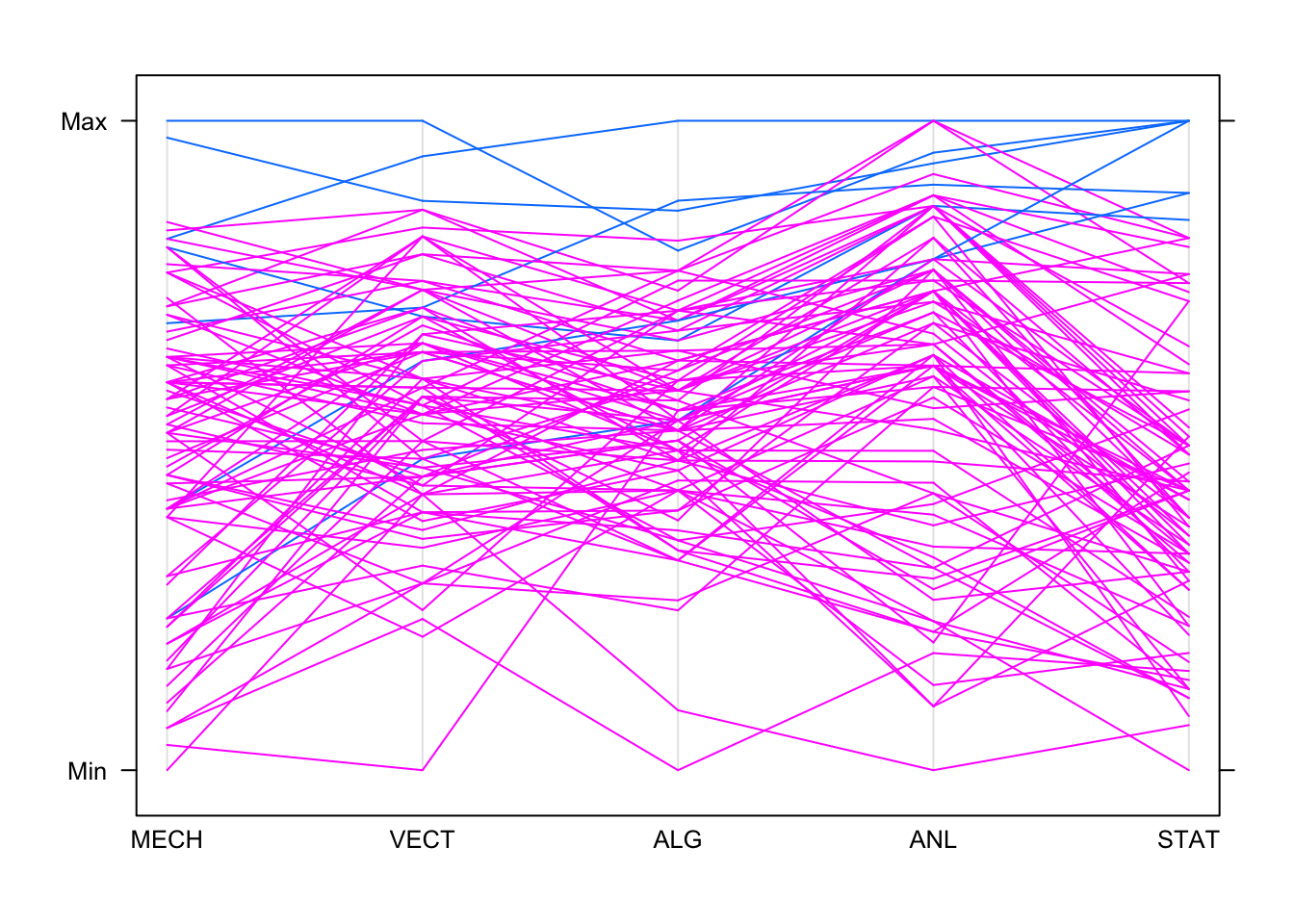

So high achievers on Stats generally do well on Analysis. Some do well on the other subjects, but performance drops and becomes more variable as we move left in the plot! One feature we can read from the PCP is when the values correspond to the same data point - for example, we can see the top student on algebra (ALG) was also top on analysis (ANL) and stats (STAT), and did pretty well on mechanics (MECH).

In the scatterplot matrix, since each panel only displays two variables it is not always clear how the points in each panel relate to the points in the other panels.

1.3 Data set 1: Crime in the USA

Download data: crime.us

The data set crime.us includes the crime totals and rates (per 100,000 population) for 50 US states during 2009. There are 16 variables, which we can separate into a small number of groups:

  • State and Population - the name and population of the state
  • Totals: total crime numbers for 7 crime categories - Murder, Rape, Robbery, Assault, Burglary, LarcenyTheft, MotorVehicleTheft
  • Rates: rates per 100,000 for 9 crime categories - ViolentCrimeRate, MurderRate, RapeRate, RobberyRate, AssaultRate, BurglaryRate, LarcenyTheftRate, MotorVehicleTheftRate
  • First, take a quick look at the first few rows of the data using the head function.
  • As the data are a mix of continuous and categorical variables, we can’t simply pass the whole data set into the pairs function.
  • Use the names function to get a list of the variable names. Which columns correspond to the rates for the various crimes?
  • Draw a scatterplot matrix of just the 9 crime rates. Hint: select a subset of the columns corresponding to the variables of interest.
  • What patterns and associations can you see?
  • The crimes can be divided into Violent crimes (Murder, Rape, Robbery, Assault), and Property crimes (Burglary, Larceny Theft, Motor Vehicle Theft). Do you find different patterns of association among similar crimes?
  • Are there any obvious outliers? If so, try and identify which State they are from the data, and use colour to highlight them on your scatterplot.
  • Make a parallel coordinate plot and use it to investigate these outliers across all the variables.
  • Have a quick look at the scatterplot matrix of the crime totals. Why do you think we focussed on the rates in our analysis above?

1.4 Data set 2: Crabs

Download data: crabs

The crabs data concerns different measurements made on 50 crabs each of two colours and both sexes of the species Leptograpsus variegatus, collected in Australia. This gives 200 total data points on each of the following variables:

  • sp - the colour species of crab, either "B" for blue or "O" for orange
  • sex
  • index - index 1:50 within each groups
  • FL - frontal lobe size (mm)
  • RW - rear width (mm)
  • CL - carapace length (mm)
  • CW - carapace width (mm)
  • BD - body depth (mm).
It’s the last five variables that are of interest to us (to begin with). As animals (and people) generally keep of their features in proportion as they grow, regardless of their size. We might expect to find some strong associations here (tall people typically have long arms and long legs, but rarely short arms and extra long legs).
  • Again, take a quick look at the first few rows of the data using the head function.
  • Make a quick scatterplot matrix of the five measurement variables. What do you see?
  • Try a parallel coordinate plot, how does the strong association appear in the plot?
The parallel coordinate plot is a jumble of (arbitrarily generated) colours. Let’s use colour more effectively to show the different species of crab. We can colour different subgroups in the data by assigning the optional groups argument to a categorical variable which defines the groups.
  • Redraw your parallel coordinate plot, but add the extra argument groups=crabs$sp.
  • Can you figure out which colour is which species? Hint identify the colour of the smallest FL value, then find that in the data.
  • What differences can you see between the different species?
  • Now colour by sex instead - do you find any featuers of interest?

One problem with data like these is that the many strong associations mean that large values on one variable are associated with other large values, since it is the overall size of the animal that changes most and all the features remain in roughly the same proportion. To highlight any deviations from the usual pattern, we could look at the relative sizes of the different features - in this case compared to the carapace length (CL).

## divide `FL` by `CL` and create a new variable in the data frame called `FLCL`
crabs$FLCL <- crabs$FL/crabs$CL 
## repeat!
crabs$RWCL <- crabs$RW/crabs$CL
crabs$CWCL <- crabs$CW/crabs$CL
crabs$BDCL <- crabs$BD/crabs$CL

Of course, now we only have four variables to work with (since CL/CL just gives us 1, so that’s not useful).

  • Scale the variables using the code above, and make a new plot of these four new variables and colour by species.
  • Can you spot any interesting differences now?
  • Experiment with plotting the variables in a different order to emphasise the differences between the two groups.
  • If you had to classify the crabs into two species, which variables would you use and how would you classify?

1.5 Variations on Standard Plots : Radar charts

If you thought the parallel coordinate plot was too much, then the radar chart (also called spider or web or polar charts) will be a step too far. While similar in concept to the parallel coordinate plot, the radar chart arranges each variable’s axis as equally-spaced spokes around a circle. The data points are still drawn with lines on these radial axes, but now their connnecting lines wind around the centre point.

library(fmsb)
colours <- alpha(rep('black',length=nrow(marks)),0.4)
colours[81] <- 'red'
radarchart(marks,maxmin=FALSE, pcol=colours, plty=1)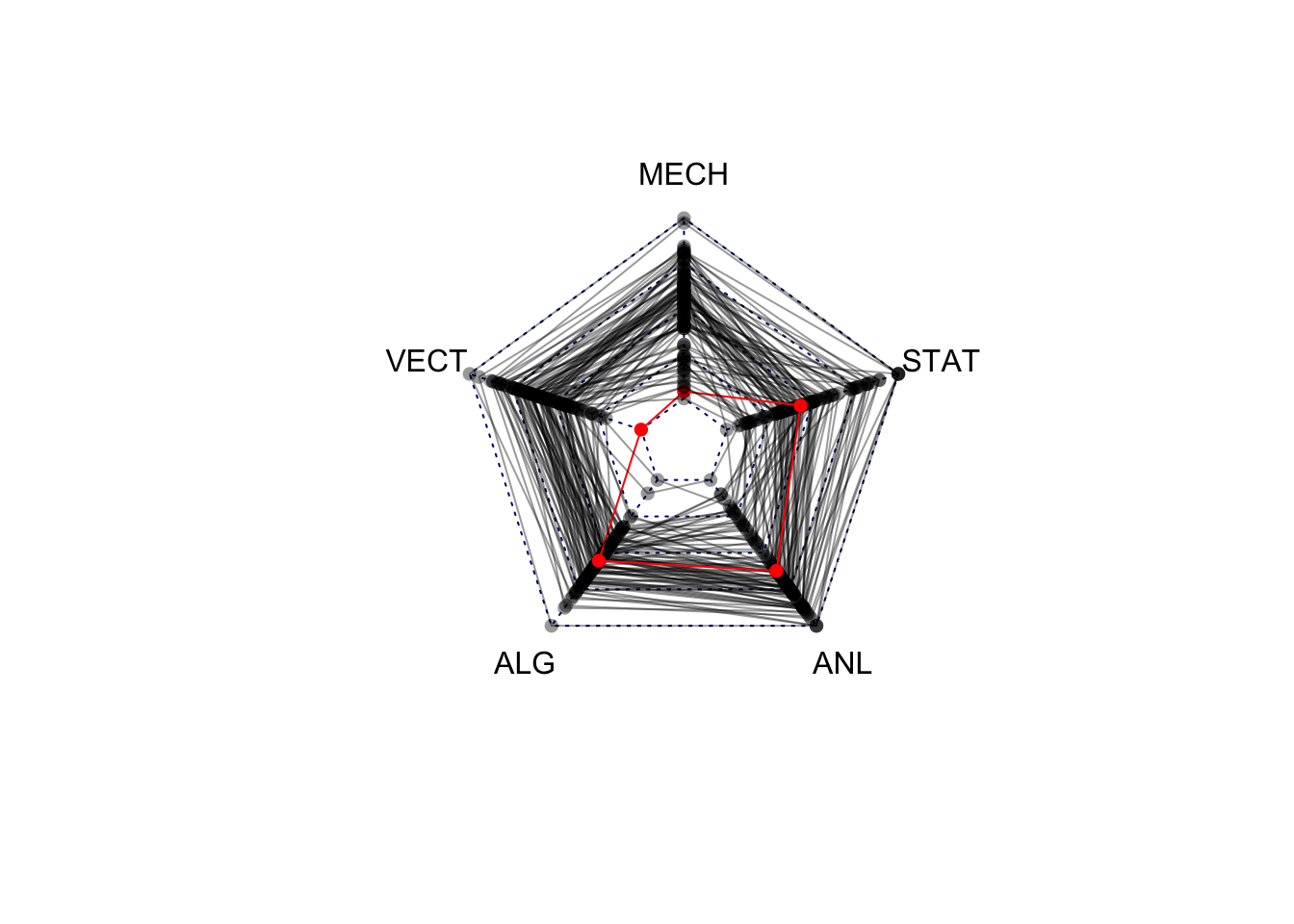

2 Getting an Overview

When you first start work on a dataset it is important to learn what variables it includes and what the data are like. There will usually be some initial analysis goals, but it is still necessary to look over the dataset to ensure that you know what you are dealing with. There could be issues of data quality, perhaps missing values or outliers, and there could be some surprising basic statistics.

There are many ways to get an initial impression of a new data set, and we’ve seen a lot of the techniques already:

  • Inspect the data values - use the head or View functions
  • Calculate simple statistical summaries - use the summary or fivenum functions
  • Separate the quantitative from categorical variable - use subsetting to split the data up
  • Draw simple univariate summary plots for each variable - use par(mfrow=c(x,y)) to create a grid of plots, and use hist or barplot to plot the individual variables; use boxplot to draw a boxplot of all quantitative variables.
  • Look for associations and relationships - use the pairs function to draw a scatterplot matrix of the quantitative variables, or a matrix of two-way mosaic plots of the categorical variables.

A correlation plot or corrplot can help give a summary version of a scatterplot matrix, useful when the number of variables to plot is large.

In addition to these techniques, there are a few plot types that can help us visualise the entire data set in one go. Rather than focussing on general behaviour between variables, these methods focus on visualising the different data points to see how the points differ from one another. We’ll look at three graphs, suitable for getting an overview of quantitative variables:

  • Corrplots
  • A heatmap
  • A glyph or star plot
  • Chernoff faces

To illustrate these plots, we’ll use the US crime statitsics data set from Workshop 3.

Download data: crime.us

2.1 Corrplots

A simple summary of the strength of the (linear) association between a pair of variables is its correlation. When we have a collection of quantitative variables, we can evaluate the correlation matrix using the cor function. Values close to \(1\) or \(-1\) indicate strong linear relationships, values close to \(0\) indicate a lack of a linear relationship.

The correlation matrix can be visualised as a simple alternative to a scatterplot matrix suitable for problems when the number of variables is too large to read the individual scatterplots.

round(cor(crime.us[,10:16]),2)
##                       MurderRate RapeRate RobberyRate AssaultRate BurglaryRate LarcenyTheftRate
## MurderRate                  1.00     0.07        0.66        0.71         0.72             0.42
## RapeRate                    0.07     1.00       -0.16        0.38         0.20             0.18
## RobberyRate                 0.66    -0.16        1.00        0.58         0.49             0.32
## AssaultRate                 0.71     0.38        0.58        1.00         0.61             0.50
## BurglaryRate                0.72     0.20        0.49        0.61         1.00             0.69
## LarcenyTheftRate            0.42     0.18        0.32        0.50         0.69             1.00
## MotorVehicleTheftRate       0.49     0.15        0.63        0.54         0.52             0.53
##                       MotorVehicleTheftRate
## MurderRate                             0.49
## RapeRate                               0.15
## RobberyRate                            0.63
## AssaultRate                            0.54
## BurglaryRate                           0.52
## LarcenyTheftRate                       0.53
## MotorVehicleTheftRate                  1.00
library(corrplot)
corrplot(cor(crime.us[,10:16]),tl.cex=0.75)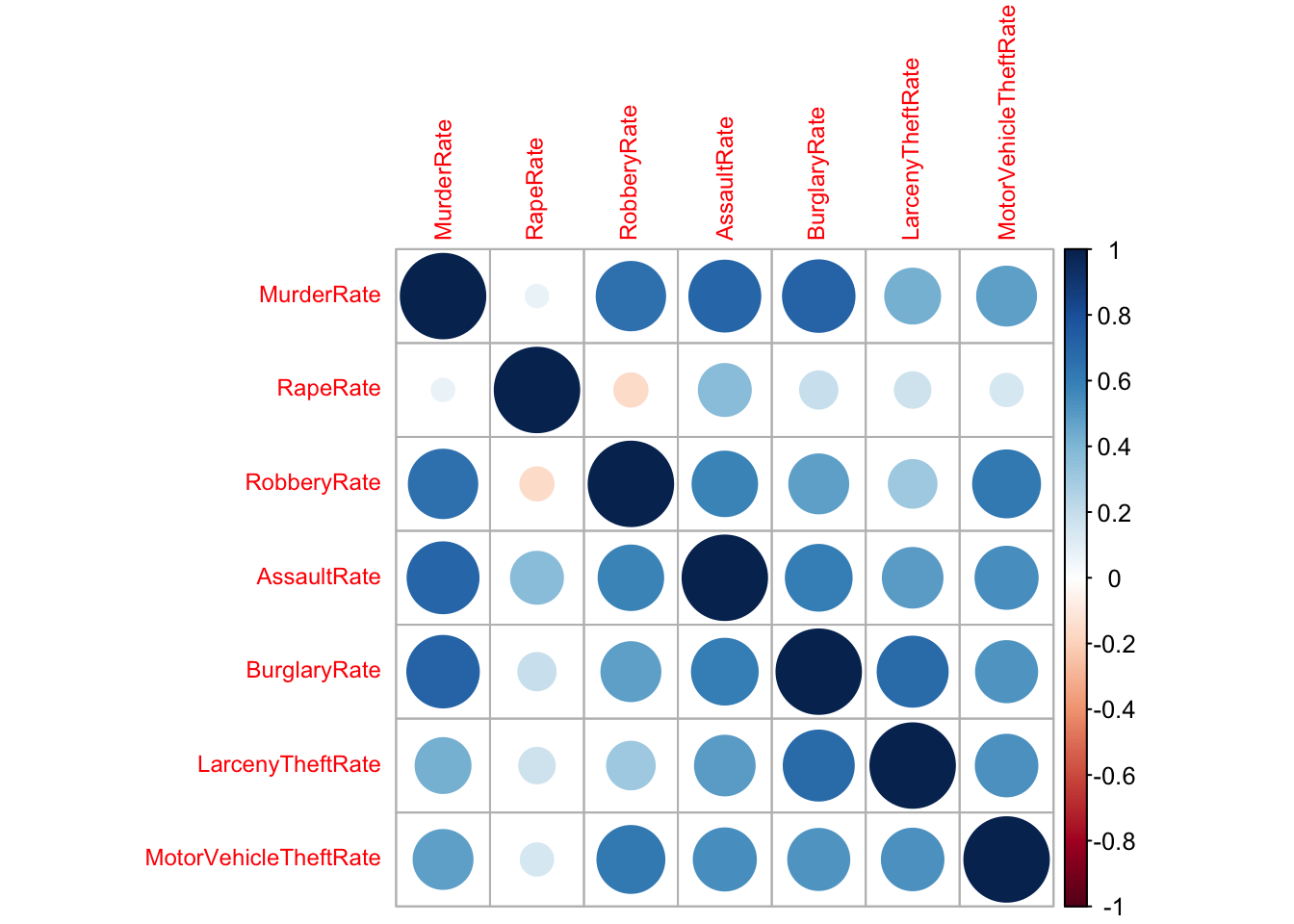

2.2 Heatmaps

With a heatmap each data point is represented by a row and each variable by a column. The individual cells are coloured according to the case value relative to the other values in the column. For this purpose, the variables are standardised individually, either with a normal transformation to \(z\) scores (i.e. subtract the mean and divide by the standard deviation) or adjusted to a scale from minimum to maximum.

We will use the function heatmap.2 from the gplots package, which uses a \(z\) scaling of the data. Let’s draw a heatmap of the crime rate variables (columns 10 to 16)

## add the state names as row labels
rownames(crime.us) <- crime.us$State
## draw the heatmap
library(gplots)
hmap <- heatmap.2(as.matrix(crime.us[,10:16]),
                  scale='column', # scale the data by the column
                  trace='none', cexCol=0.75) # shrink the column labels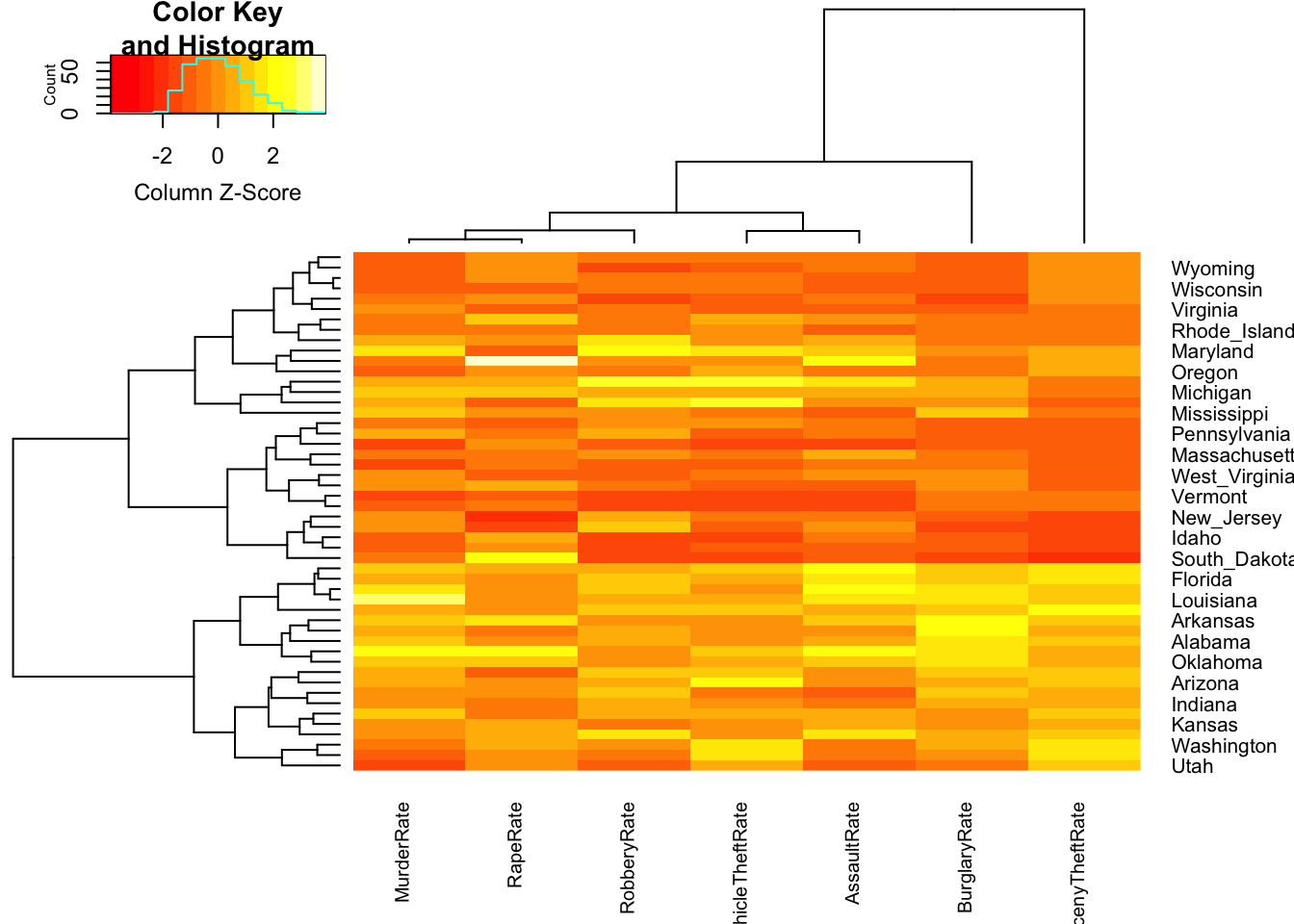

The colours within each column range from red (low values) through to yellow (high values). The rows in the data have been permuted to emphasise difference between the different cases, and here we can observe a block of data points in the lower half of the plot with particularly large values (lots of yellows) of Larceny and Burglary. Looking closer at the labels, we note that most of the states in this group seem to correspond to States in the South. We can also spot a white cell in the RapeRate column corresponding to Alaska, which we previously noted.

The tree structures on the left and above the plot show a clustering of the data cases (left) into groups of similar points, and a clustering of the variables (above). You’ll see more on clustering later.

2.3 Glyphs

With glyphs, each case is represented by a multivariate symbol reflecting the case’s variable values. As for heatmaps, each variable must be standardised in some way first and this can influence the w

stars(crime.us[,10:16],draw.segments=TRUE)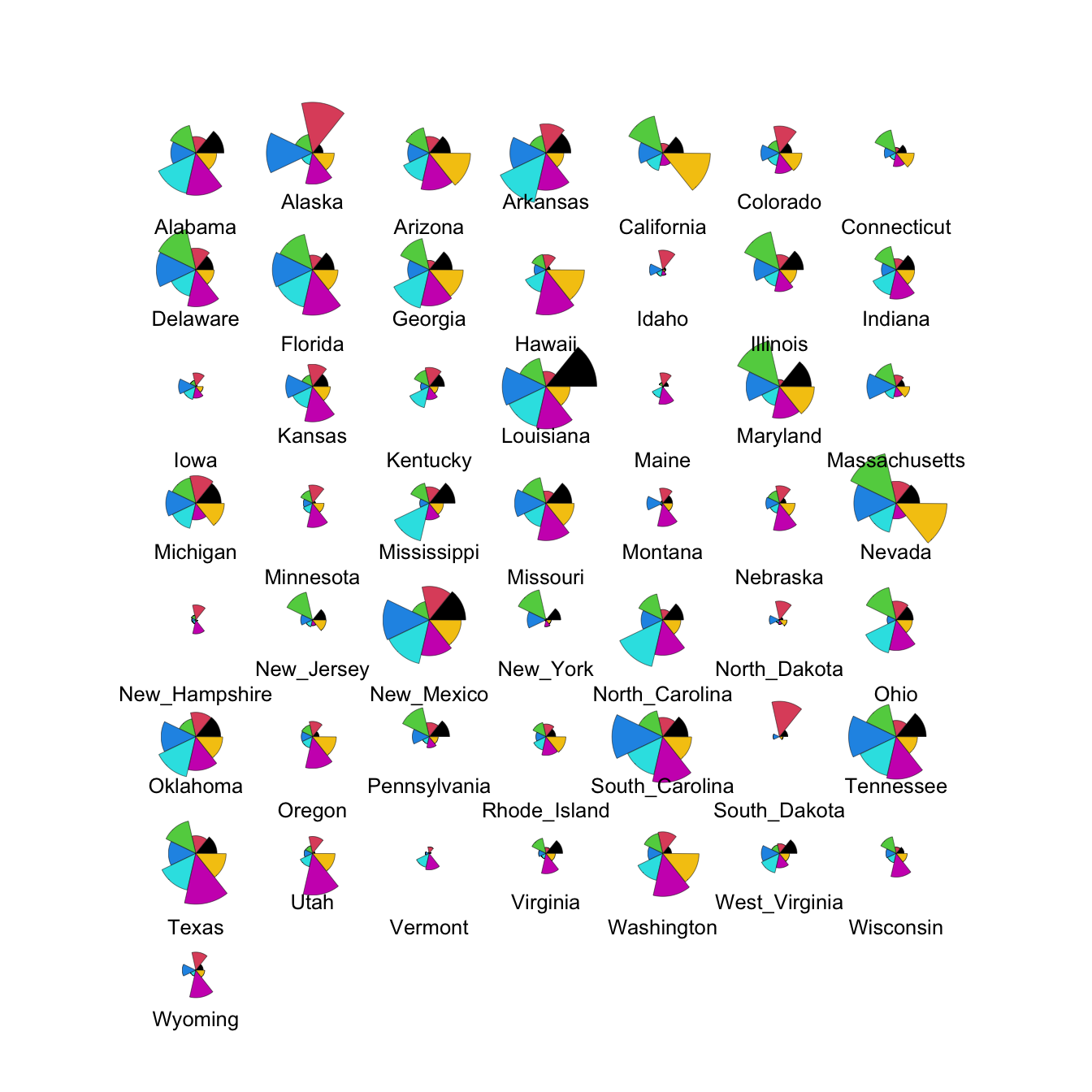

We can modify this to show the data cases in the same order as the heatmap by extracting the ordering from the heatmap output (in the rowInd component) and using it to rearrange our data set. We can also set custom colours to make things prettier!

stars(crime.us[hmap$rowInd,10:16], draw.segments=TRUE)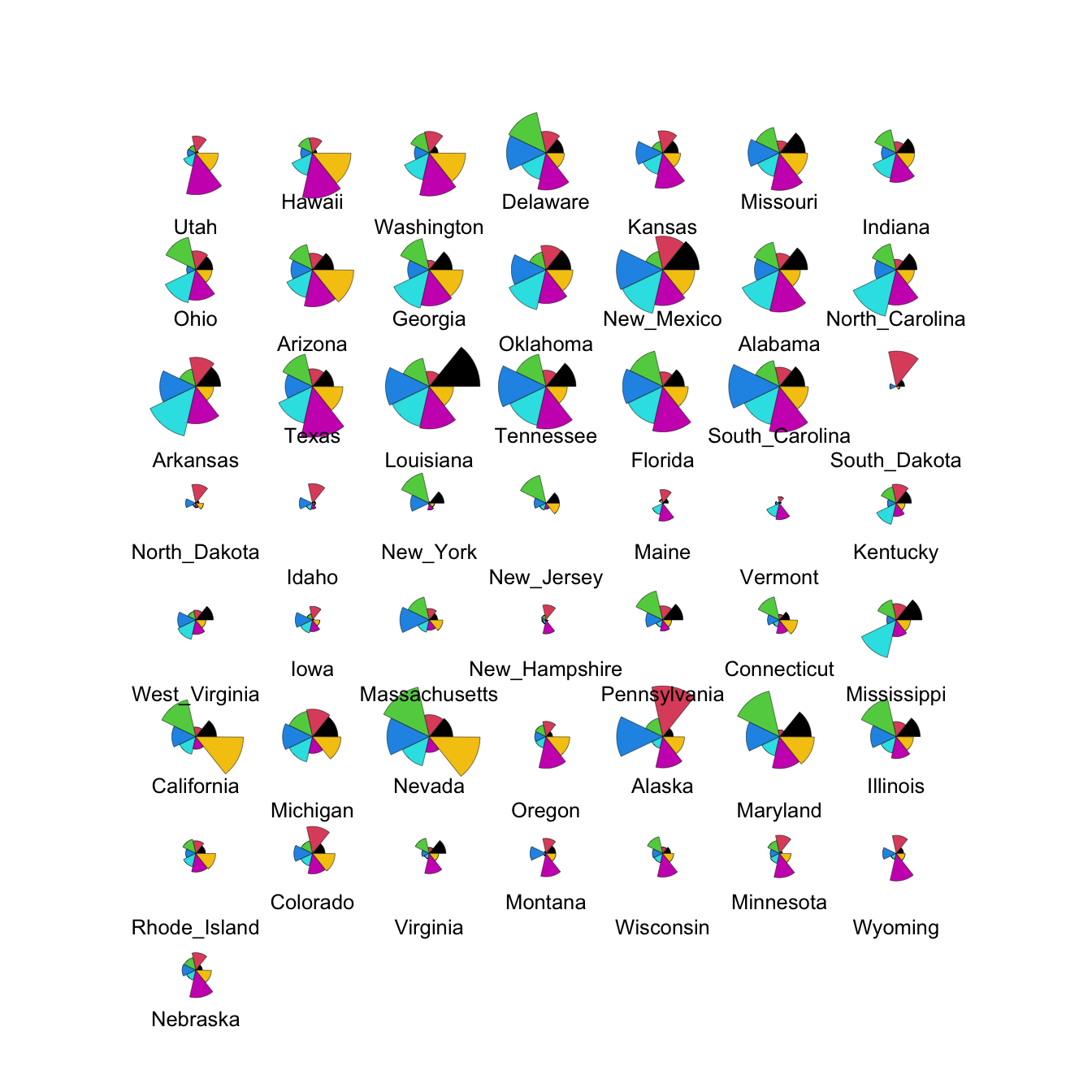

The large values on the southern states stand out quite clearly now in the top block of cases.

2.4 Chernoff faces

This one is a little nuts, and is more of a curiosity than anything.

Chernoff faces display multivariate data in the shape of a human face. The idea behind using faces is that humans easily recognize faces and notice small changes without difficulty. Chernoff faces handle each variable differently. Because the features of the faces vary in perceived importance, the way in which variables are mapped to the features should be carefully chosen.

library(TeachingDemos)
faces(crime.us[hmap$rowInd,10:16])

I’m not sure its particularly helpful or particularly effective as a visualisation, but it is another variation on the idea of a glyph plot.

2.5 Data Set: The Guardian University League Table 2013

Download data: uniranks

We’ve looked at these data before, in Lecture 2 where we explored the parallel coordinate plot. Let’s use this as an example data set for exploring some of the techniques above. The data set contains a number of variables for 120 UK universities:

  • Rank - Overall rank of the University in the League Table
  • Institution - University name
  • UniGroup - Universities can be a member of one of five groups, 1994 Group, Guild HE, Million+, Russell, University Alliance, or none
  • HesaCode - University’s Higher Education Statistics Agency ID code
  • AvTeachScore - Average Teaching Score
  • NSSTeaching - University’s National Student Survey teaching score
  • NSSOverall - University’s NSS overall score
  • SpendPerStudent - University expenditure per student (depends on subject)
  • StudentStaffRatio - Student to Staff ratio
  • CareerProspects - Proportion of graduates in appropriate level employment or full-time study within six months of graduation
  • ValueAddScore - ”Based upon a sophisticated indexing methodology that tracks students from enrolment to graduation, qualifications upon entry are compared with the award that a student receives at the end of their studies.” (Guardian)
  • EntryTariff - Value dependent on the average points needed to get on the university’s courses
  • NSSFeedback - University’s NSS feedback score
  • Load the data, and extract the numerical variables.
  • Apply the graphical techniques above - what features can you see?
  • How would you explore behaviour of the different University groups?

3 More Practice

3.1 Data set: Fertility in Switzerland

The built-in R dataset swiss contains a standardised fertility measure and various socio-economic indicators for each of the 47 French-speaking provinces of Switzerland in about 1888. The six variables it contains are:

  • Fertility - ‘common standardized fertility measure’
  • Agriculture - % of males involved in agriculture as occupation
  • Examination - % draftees receiving highest mark on army examination
  • Education - % education beyond primary school for draftees.
  • Catholic - % ‘catholic’ (as opposed to ‘protestant’).
  • Infant.Mortality - live births who live less than 1 year.
  • Draw a parallel coordinate plot of all six variables
  • Are there any cases that might be outliers on one or more variables?
  • What can you say about the distribution of the variable Catholic?
  • Construct a new variable with values High for all provinces with more than 80% Catholics and Lower for the rest. Draw a pcp coloured by the groups of the new variable. How would you describe the features you see?

3.2 Data set: Bodyfat

Download data: bodyfat

The dataset bodyfat gives estimates of the percentage of body fat (bodyfat) of 252 men, determined by underwater weighing, alog with 10 body circumference measurements, height, weight and body density. The data set has often been used to illustrate regression to see if body fat percentage can be predicted from the other variables.

  • Draw a parallel coordinate plot and attempt to answer the following questions (don’t look at other plots just yet)
    • Are there any outliers? What can you say about them?
    • Can you deduce anything about the height variable?
    • What can you say about the relationship between the first two variables density and bodyfat?
    • Do you think that the orderings of the variables is sensible? Experiment reordering the variables to try and make a more informative plot.
  • Now look at the scatterplot matrix for these data.
    • You may need to use transparency here!
    • How would you answer the questions above using the scatterplot matrix?