Workshop 2 - Principal Component Analysis
Workshop 2: Principal Component Analysis
Principal component analysis (PCA) is a technique that produces a smaller set of uncorrelated variables from a larger set of correlated variables. This allows to visualize, explore, and discover hidden features of the data set. It is also very useful to perform a special type of multilinear regression (see Principal Components Regression). Here we explore how to perform PCA using R, how to read and visualize the output, as well as good practices and how to avoid pitfalls. For a more theoretical viewpoint on PCA, you are referred to the lecture notes.
In R, PCA is performed using either
princomp() or prcomp() (the latter being the preferred
method).
Iris data
Let us put this into practice with the Iris data set. You get the
data in R by typing data(iris) in the console (the data set
is also on Blackboard in a csv file iris.csv).
We begin by reading the data into R and printing out the first six rows of the data.
head(iris)## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 1 5.1 3.5 1.4 0.2 setosa
## 2 4.9 3.0 1.4 0.2 setosa
## 3 4.7 3.2 1.3 0.2 setosa
## 4 4.6 3.1 1.5 0.2 setosa
## 5 5.0 3.6 1.4 0.2 setosa
## 6 5.4 3.9 1.7 0.4 setosaWe can also look at the summary statistics of the numerical variables:
summary(iris[,-5])## Sepal.Length Sepal.Width Petal.Length Petal.Width
## Min. :4.300 Min. :2.000 Min. :1.000 Min. :0.100
## 1st Qu.:5.100 1st Qu.:2.800 1st Qu.:1.600 1st Qu.:0.300
## Median :5.800 Median :3.000 Median :4.350 Median :1.300
## Mean :5.843 Mean :3.057 Mean :3.758 Mean :1.199
## 3rd Qu.:6.400 3rd Qu.:3.300 3rd Qu.:5.100 3rd Qu.:1.800
## Max. :7.900 Max. :4.400 Max. :6.900 Max. :2.500Finally, we can plot a scatter plot matrix using
pairs.panels function in the psych package:
#install.packages('psych')
library(psych)
pairs.panels(iris[,-5],
method = "pearson", # correlation method
hist.col = "#00AFBB",
density = TRUE, # show density plots
ellipses = TRUE # show correlation ellipses
)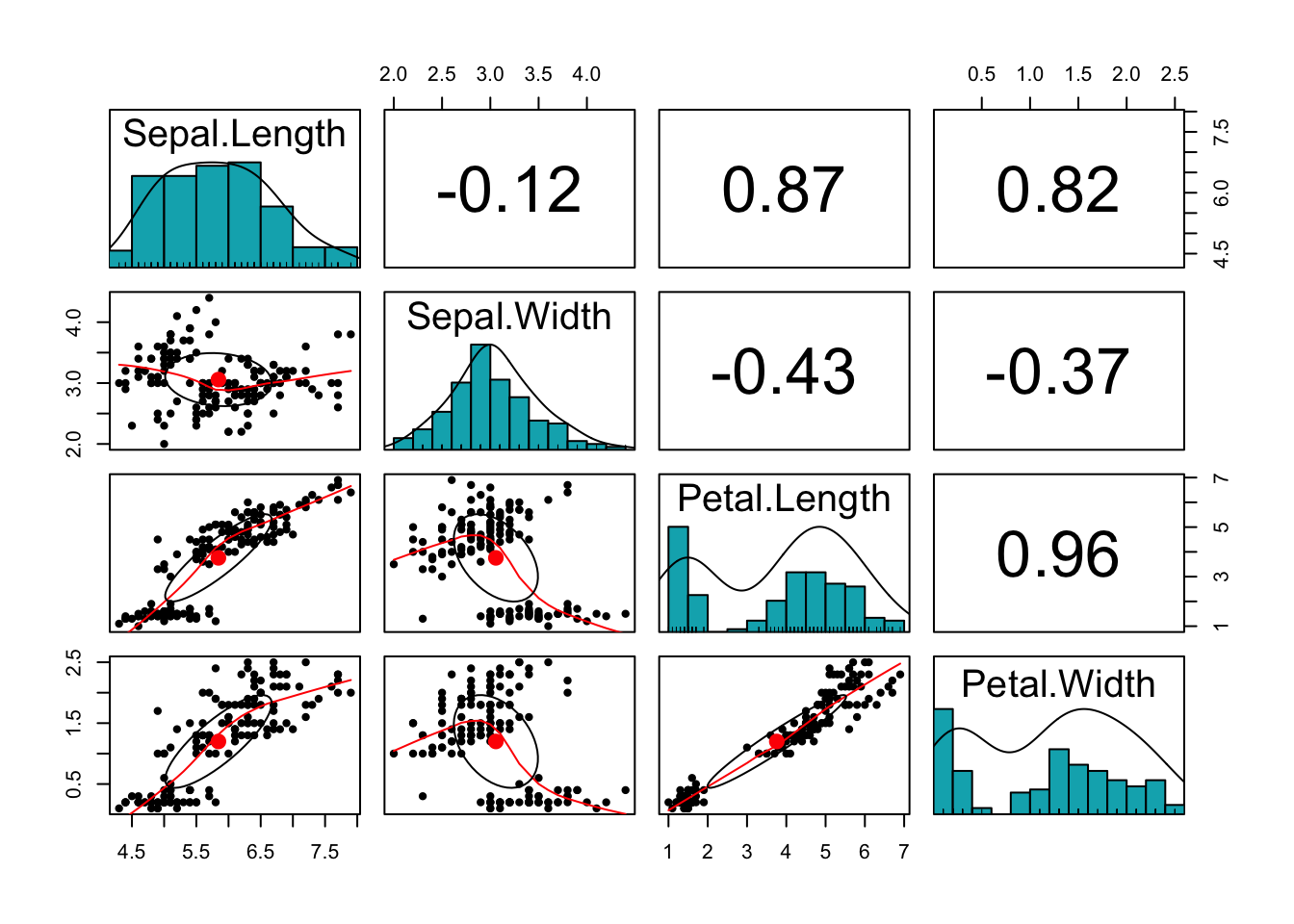
What can you say about the plot? Do the variables share sufficient information to warrant redundancy?
You can see that the Petal variables are highly correlated (correlation =0.96). They are also highly correlated with the Sepal length variable. This implies that the three variables share redundant information and the use of PCA can remove this redundancy, thereby reducing the dimension of the data.
Let us explore how the function prcomp() can help us with dimension reduction:
dat <- iris[,-5]
pr.out <- prcomp(dat, scale = TRUE)
names(pr.out)## [1] "sdev" "rotation" "center" "scale" "x"summary(pr.out)## Importance of components:
## PC1 PC2 PC3 PC4
## Standard deviation 1.7084 0.9560 0.38309 0.14393
## Proportion of Variance 0.7296 0.2285 0.03669 0.00518
## Cumulative Proportion 0.7296 0.9581 0.99482 1.00000We find here five quantities of interest. The most important are
sdev and rotation.
pr.out$rotation## PC1 PC2 PC3 PC4
## Sepal.Length 0.5210659 -0.37741762 0.7195664 0.2612863
## Sepal.Width -0.2693474 -0.92329566 -0.2443818 -0.1235096
## Petal.Length 0.5804131 -0.02449161 -0.1421264 -0.8014492
## Petal.Width 0.5648565 -0.06694199 -0.6342727 0.5235971This matrix has four columns, called \(PC1\), \(PC2\), and so on. They represent the principal components of our data set, i.e. a new basis of the data space that explains better the variability of the data. The coefficients (i.e. the numbers in each column) are called the loadings, so you will find the terminology loading vector of the principal component PC1 to mean the vector underlying PC1.
Observe: the loading vectors are pairwise orthogonal, and in fact orthonormal (each is of norm 1). Let us check this:
PC <- function(i){pr.out$rotation[,i]}
PC(1)%*%PC(2)## [,1]
## [1,] -1.249001e-16PC(1)%*%PC(1)## [,1]
## [1,] 1PC(4)%*%PC(4)## [,1]
## [1,] 1How exactly are principal components better in capturing the data variability? By design (see lectures), \(PC1\) spans the direction that captures the biggest proportion of variance in the observations, \(PC2\) is chosen among all the vectors that are orthonormal to \(PC1\) as one spanning the direction that captures the most variance, and so on. The constraint that these vectors are pairwise orthornomal reduces a lot the possible choices.
We can think about this geometrically: \(PC1\) is the closest line to the data points, \(\langle PC1, PC2 \rangle\) the closest plane to the data points, \(\langle PC1, PC2, PC3 \rangle\) the closest 3-dimensional vector space, and so on… More on this in the lectures.
To retain: the most important component is \(PC1\): it is the direction where the dataset is more variable.
How do we measure this importance?
pr.var <- pr.out$sdev^2
pr.var## [1] 2.91849782 0.91403047 0.14675688 0.02071484sum(pr.var)## [1] 4We have then discovered how the quantity given under
Importance of components are calculated: they are obtained
from the variance of the principal components. We can make a plot to
visualize this better.
plot(pr.out, col = "steelblue", main="Importance of Iris PC")
lines(x = 1:4, pr.var, type="b", pch=19, col = "red")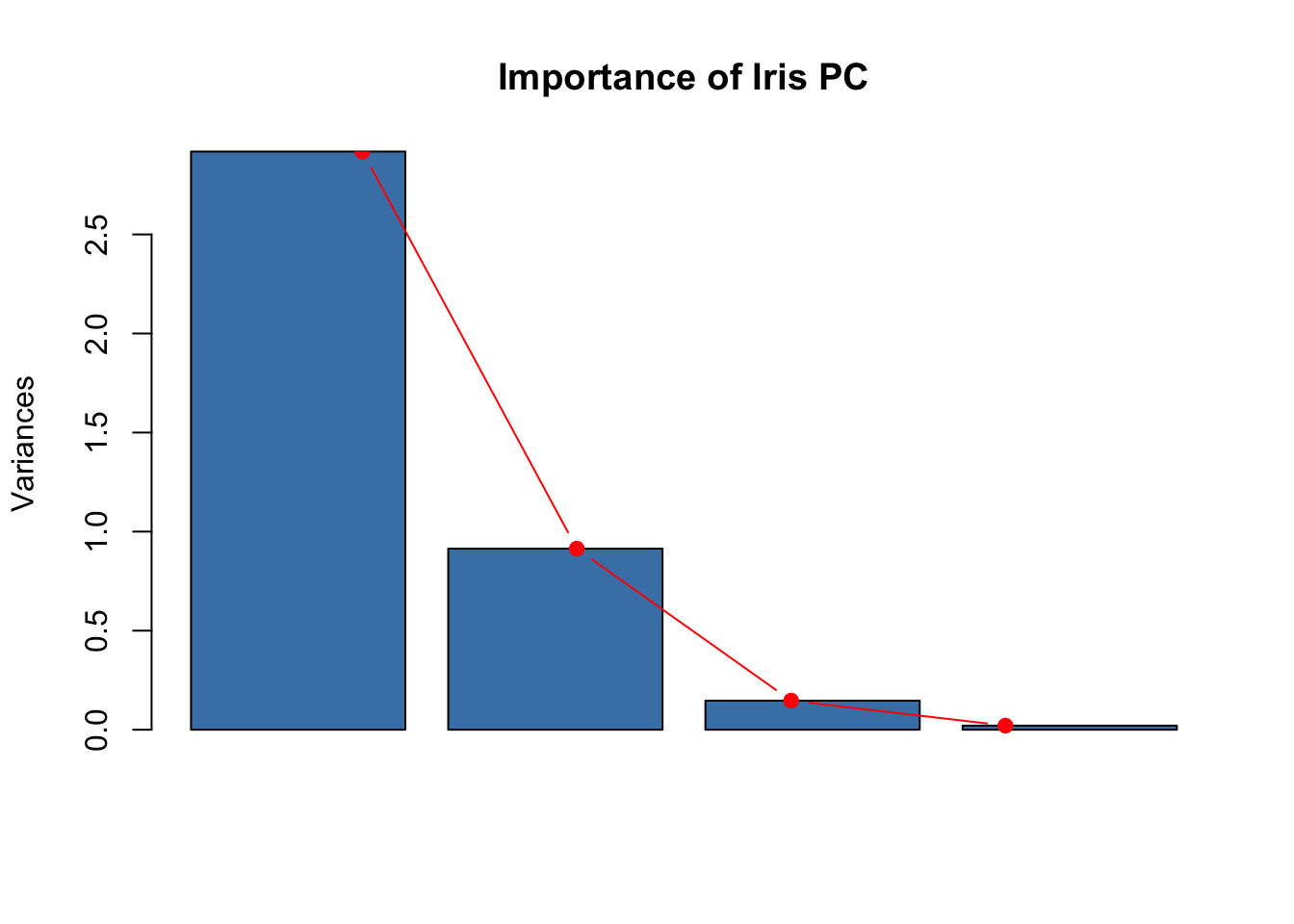
The component \(PC1\) accounts for a big proportion of variance (72.96%), \(PC2\) for some of it, and the other directions are essentially variance free. Geometrically, this means that the points are very close to the plane \(\langle PC1, PC2 \rangle\). It makes then sense to analyze and visualize our data set using this plane. How?
The most natural thing to do is to look at the position of the data
points when they get projected onto this plane. The coefficients of the
observations in the basis \((PC1, PC2, PC3,
PC4)\) are called the scores. They are the component
denoted by x in the output of prcomp()
pr.out$x
summary(pr.out$x)Note that the scores of all principal components have mean zero. Why?
Using linear algebra to compute scores [optional]
We can compute the scores of a single observation, for example the one corresponding to the first row of our data matrix, by observing that they are obtained by multiplication with the inverse of the rotation matrix. You need to recall how to make a change of basis in linear algebra to make sense of this.
sc.iris <- scale(dat)
iris.obs <- sc.iris[1,]
solve(pr.out$rotation) %*% iris.obs## [,1]
## PC1 -2.25714118
## PC2 -0.47842383
## PC3 0.12727962
## PC4 0.02408751To understand how principal components modify the datascape, we can look at the scatterplot matrix obtained by replacing the original data set with the data set of principal component scores.
pairs.panels(pr.out$x,
method = "pearson", # correlation method
hist.col = "#00AFBB",
density = TRUE, # show density plots
ellipses = TRUE # show correlation ellipses
)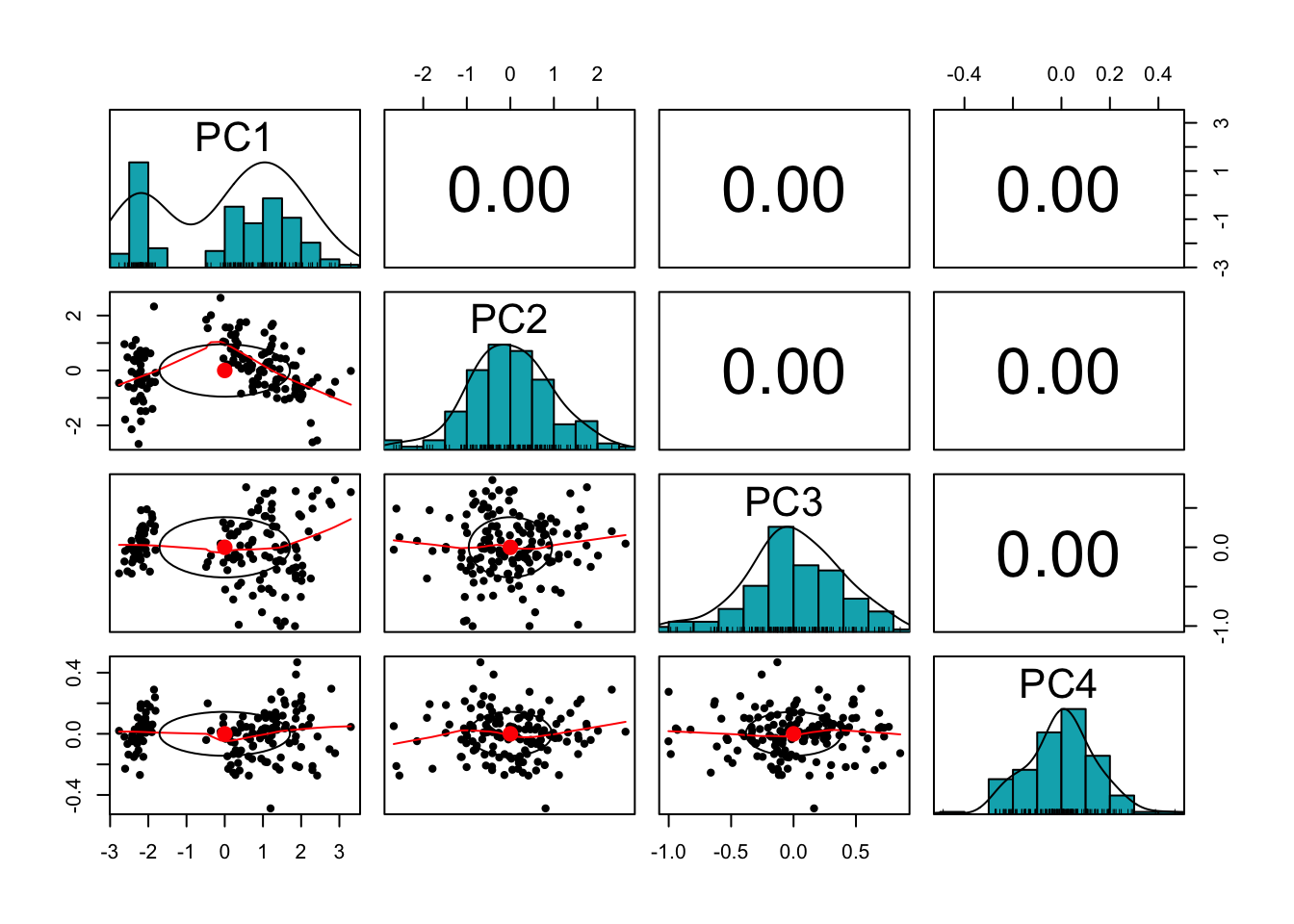
The variables are now uncorrelated! This is not a coincidence, as we will see in the lectures.
To visualize the scores of the first two principal components we don’t have to compute them one by one. The biplot() command can be used, but we can achieve a better visualization using autoplot() (from the ggfortify library)
#install.packages('ggfortify')
library(ggfortify)
autoplot(pr.out, data = iris, colour = "Species") #, label = TRUE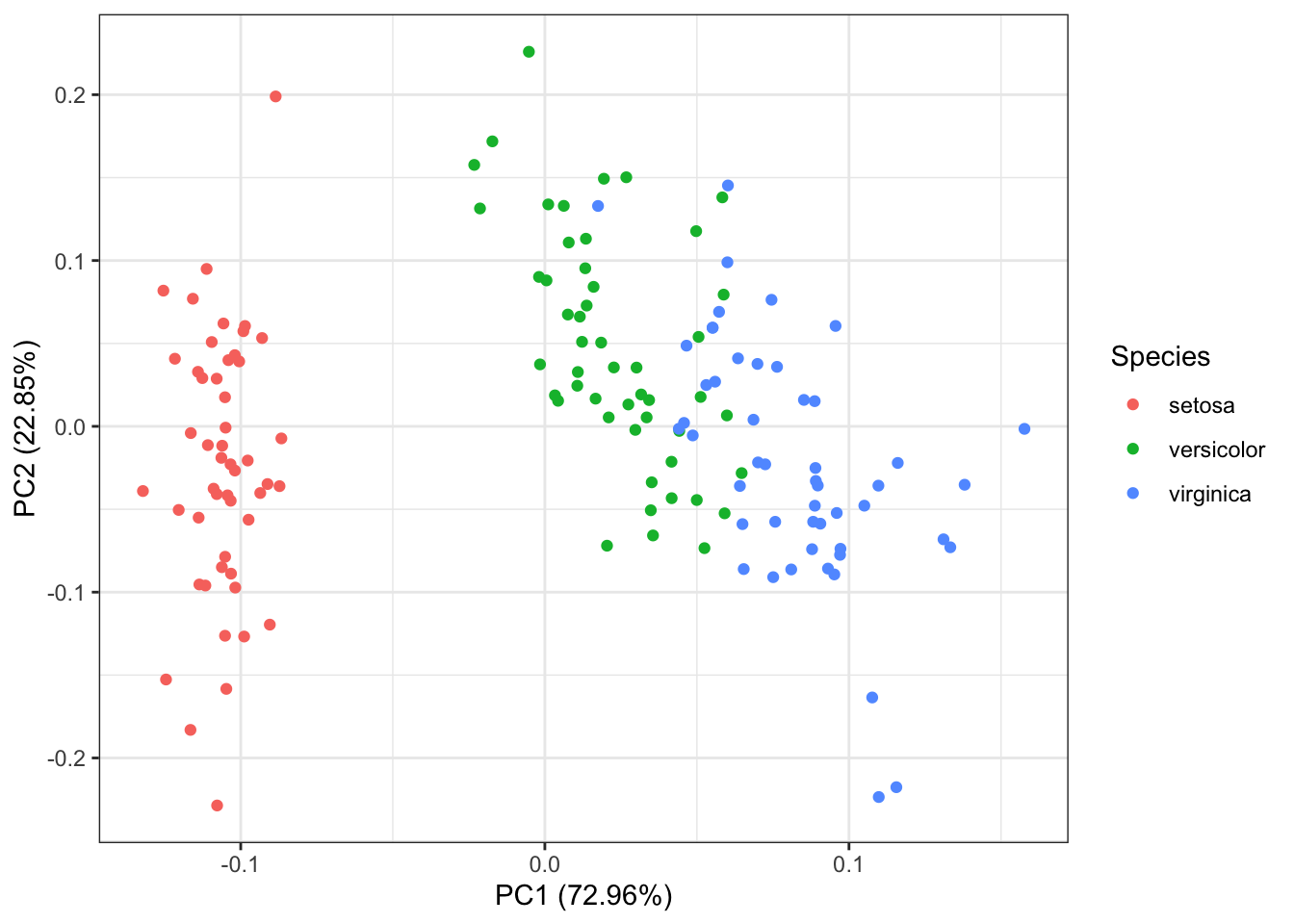
Using the option loadings, we can add to this plot the
projections of the original variables (Sepal Length, Sepal Width, etc.)
on the plane \(\langle PC1, PC2
\rangle\). This is a good way to visualize the loading
vectors.
autoplot(pr.out, data = iris, colour = 'Species',
loadings = TRUE, loadings.colour = 'blue',
loadings.label = TRUE, loadings.label.size = 3)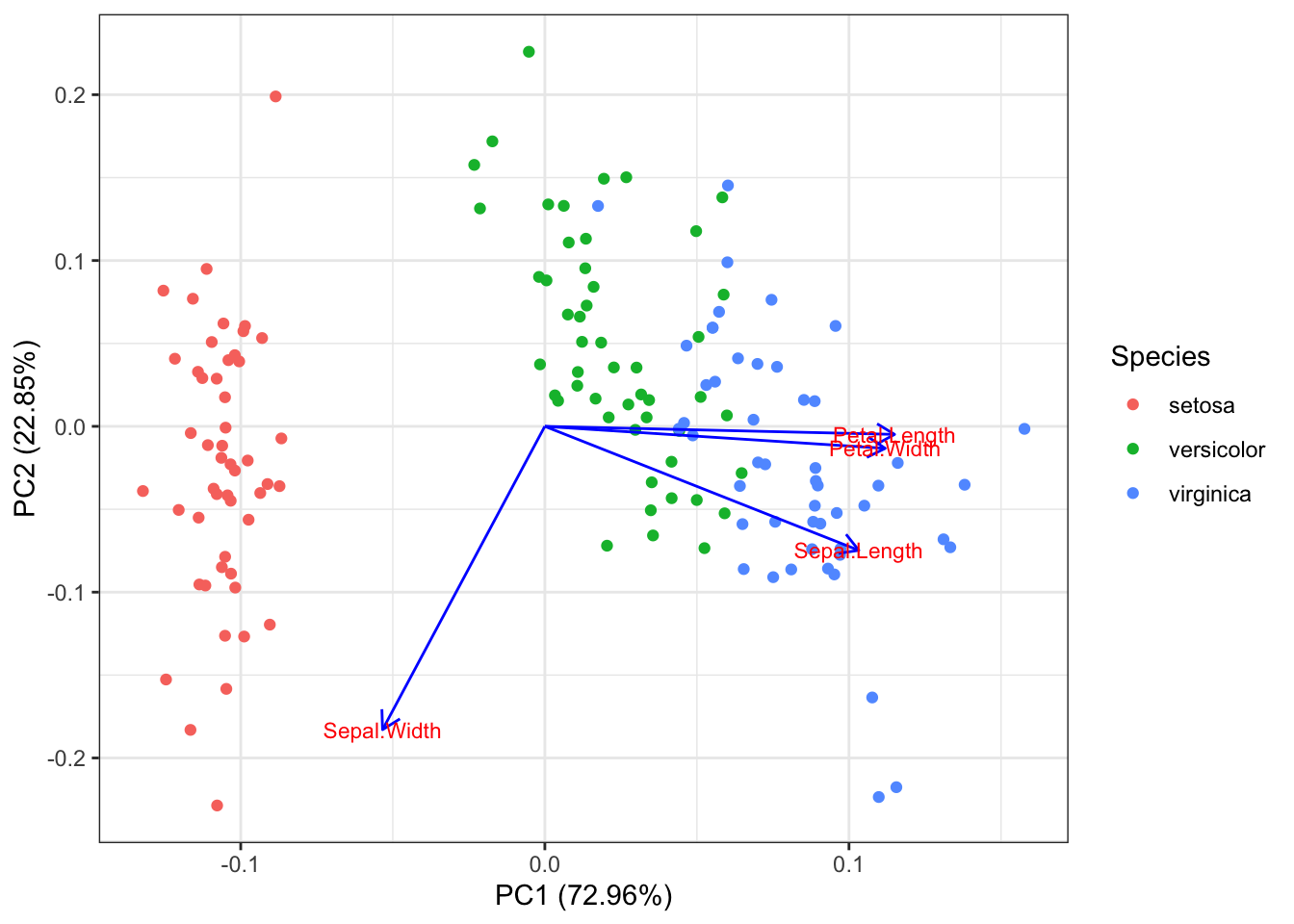
From this plot we can see how much the original variables contribute to the two first principal components. Petal length, petal width and sepal length are the features contributing the most to \(PC1\). Sepal width and Sepal length are the features that mostly contribute to \(PC2\).
The importance of scaling
In the previous example, note that we have applied PCA to the scaled iris data (through the command `scale=TRUE’).
What happens if we don’t do this?
First, we get different loading vectors:
pr2.out <- prcomp(dat)
summary(pr.out)## Importance of components:
## PC1 PC2 PC3 PC4
## Standard deviation 1.7084 0.9560 0.38309 0.14393
## Proportion of Variance 0.7296 0.2285 0.03669 0.00518
## Cumulative Proportion 0.7296 0.9581 0.99482 1.00000summary(pr2.out)## Importance of components:
## PC1 PC2 PC3 PC4
## Standard deviation 2.0563 0.49262 0.2797 0.15439
## Proportion of Variance 0.9246 0.05307 0.0171 0.00521
## Cumulative Proportion 0.9246 0.97769 0.9948 1.00000Note that the first principal component becomes much more prominent: it explains a much larger proportion of the variance. Why?
Answer
Because the feature with larger variance weights much more now!
We can verify this by comparing the standard deviations of the features:
apply(dat,2,sd)## Sepal.Length Sepal.Width Petal.Length Petal.Width
## 0.8280661 0.4358663 1.7652982 0.7622377We can clearly see that things are more skewed towards the features with larger variance (Petal Length) when we look at the loadings plot
autoplot(pr2.out, data = iris, colour = "Species", loadings = TRUE, loadings.colour = 'blue',
loadings.label = TRUE, loadings.label.size = 3)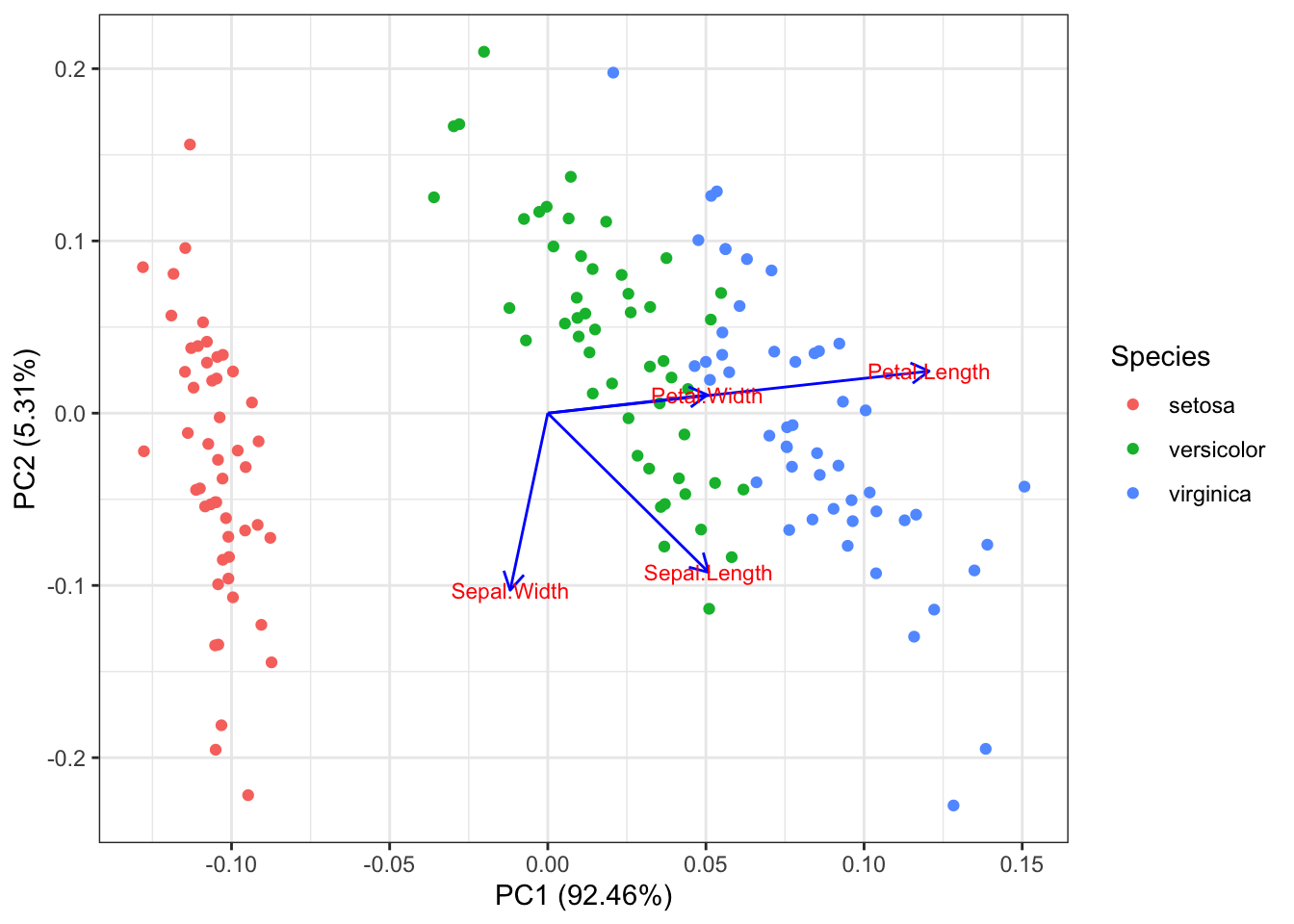
Here we were lucky because all features were expressed in the same unit (cm), but it may get worse: by changing units, variance changes too: for example if Sepal Length were to be expressed in meters, that would significantly reduce its standard deviation!
We want PCA to be independent of rescaling, so scaling the variables will help us with this issue. If the units are the same and the variances close to each other it is less problematic to not scale the data. This has the advantage to avoid a rather clumsy manipulation of the data.
Is there any situation in which it is advisable not to normalize? Yes! When the variance of the original features is important, or if one wants to give more importance to those features that have more variability. We’ll see an example in the lecture.