Workshop: Hierarchical clustering
This workshop involves the illustration of hierarchical clustering
and model based clustering using Iris data. We will have a deeper look a
the algorithm underlying hierarchical clustering and the possible ways
to visualize the output. We will also learn how to use the
agglomerative coefficient to select an appropriate
linkage method. At the end of the workshop, we will learn more about
model-based clustering and see how to implement this in
R.
Hierarchical clustering
iris.scaled <- scale(iris[, -5])The next step is to compute the Euclidean distances and hierarchical clustering with complete linkage (we will later see how other linkages affect the final result).
# Compute distances and hierarchical clustering
dd <- dist(iris.scaled, method = "euclidean")
hc <- hclust(dd, method = "complete")
hc##
## Call:
## hclust(d = dd, method = "complete")
##
## Cluster method : complete
## Distance : euclidean
## Number of objects: 150We can visualise the object by using a dendrogram. This enables us to determine the point to cut the tree and so choose the number of clusters.
dendros <- as.dendrogram(hc)
plot(dendros, main = "Iris data - Complete linkage",
ylab = "Height", cex = .01)
abline(h=0.2, lty = 2, col="red")
abline(h=0.428, lty = 2, col="blue")
Hs <- hc$height[(length(hc$height)-4):length(hc$height)]
abline(h=Hs, col=3, lty=2)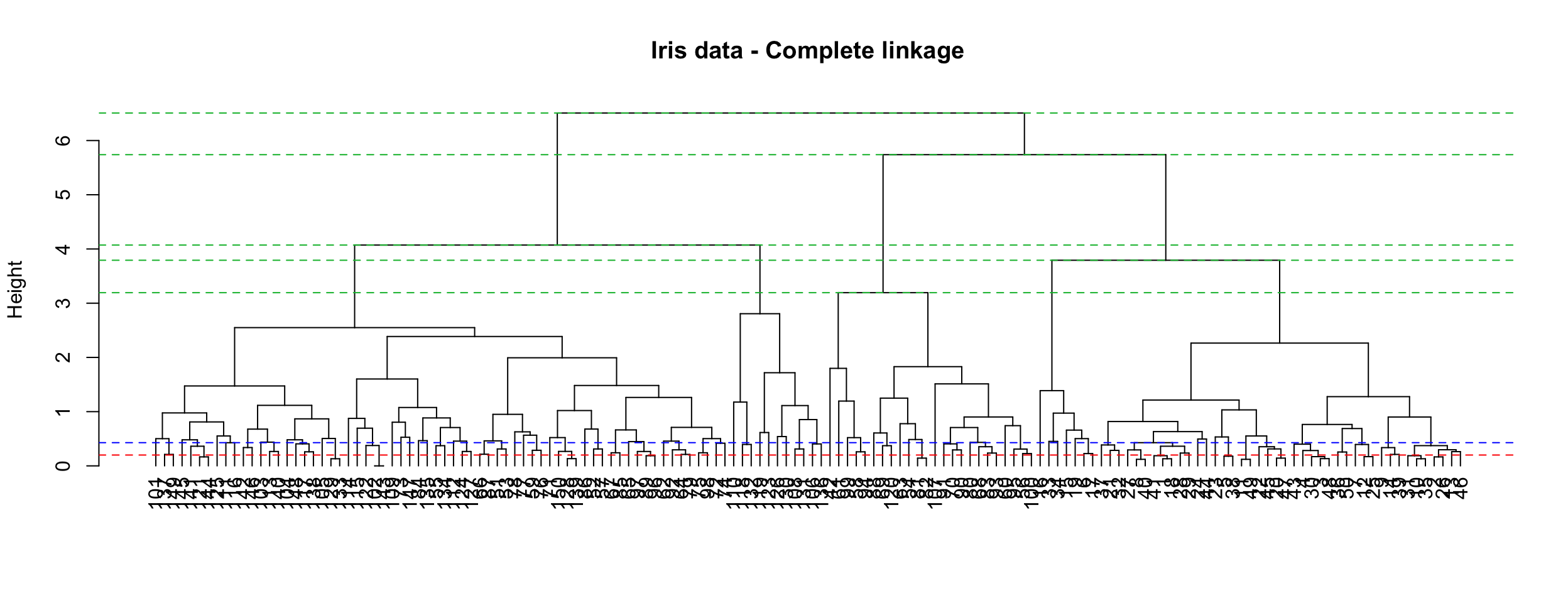
The height axis on the dendrogram displays the dissimilarity between observations and/or clusters. The horizontal bars indicate the point at which two clusters/observations are merged. For instance, observations 137 and 149 are merged at a distance (height) of 0.2 (see the red line), observations 111 and 116 are merged at a height of about 0.428 (see the blue line) and so on.
Dissimilarity scores between merged clusters only increase as we agglomerate clusters together. In other words, we can always draw a proper dendrogram, where the height of a parent is always higher than height of its children. This property is called no inversion property which is illustrated with dashed green lines in the plot.
Visualisation of the plot above can be improved by using the
fviz_cluster() and fviz_dend() functions in the
factoextra package.
library(factoextra)
par(mfrow=c(1, 2))
fviz_cluster(list(data=iris.scaled, cluster=cutree(hc, 3)), ellipse.type = "norm")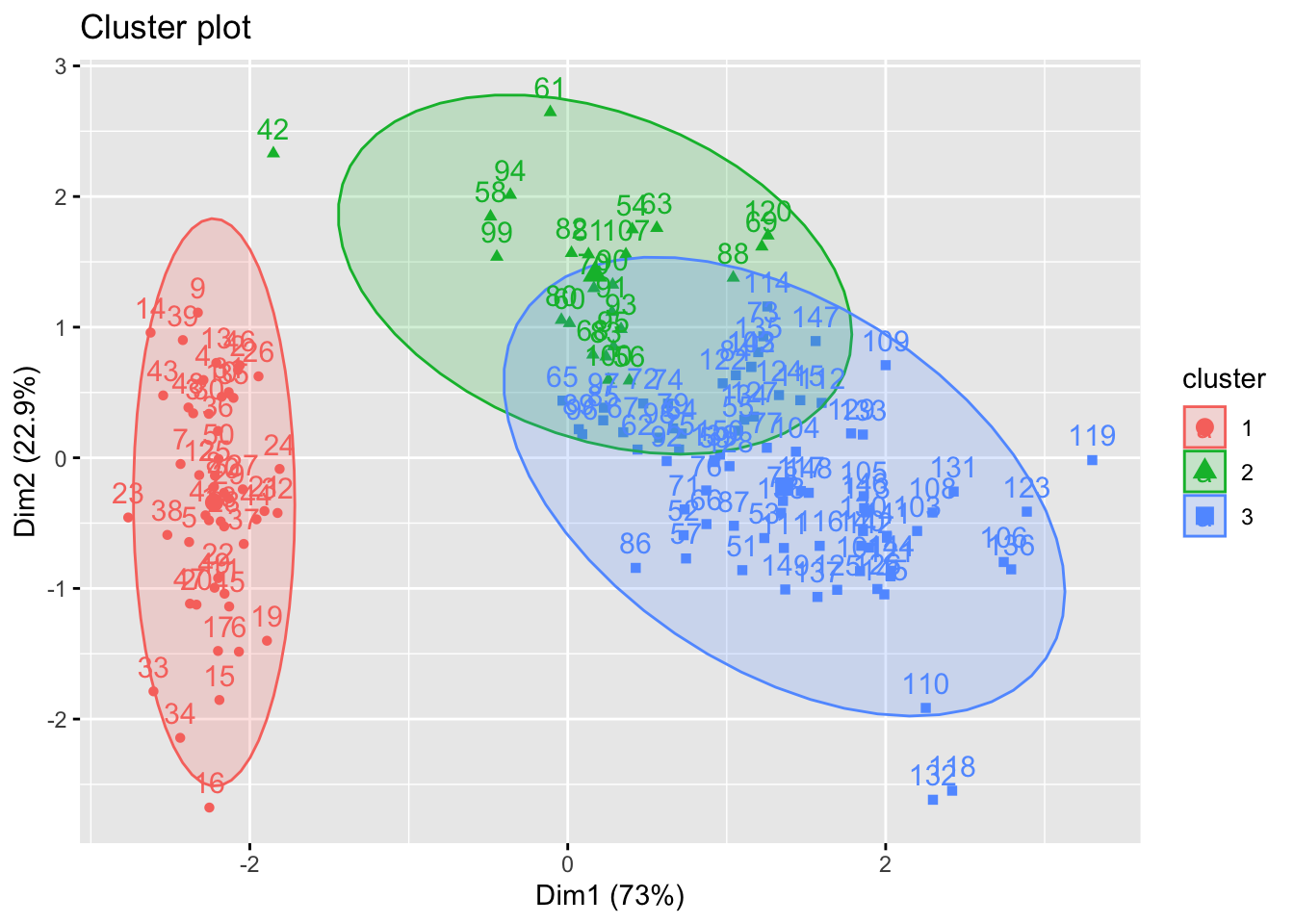
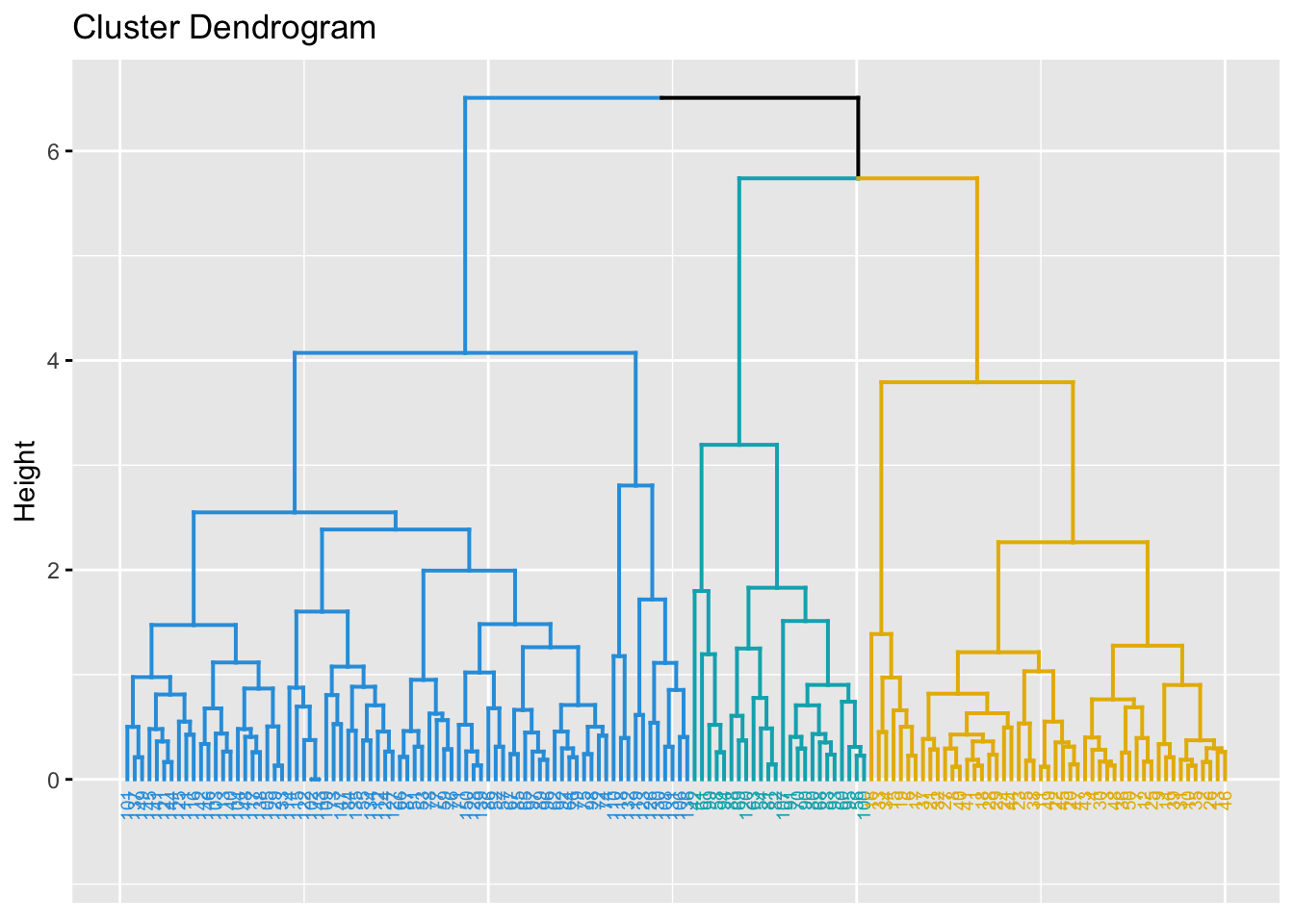
fviz_dend(hc, k = 3, # Cut in three groups
cex = 0.5, # label size
k_colors = c("#2E9FDF", "#00AFBB", "#E7B800"),
color_labels_by_k = TRUE, # color labels by groups
ggtheme = theme_gray() # Change theme
)
We can also examine the number of observations in each of the three clusters.
hcut <- cutree(hc, k = 3)
table(hcut)## hcut
## 1 2 3
## 49 24 77The aggregate() function can be used to compute the means of the features in each cluster.
aggregate(iris[, -5], by=list(cluster=hcut), mean)## cluster Sepal.Length Sepal.Width Petal.Length Petal.Width
## 1 1 5.016327 3.451020 1.465306 0.244898
## 2 2 5.512500 2.466667 3.866667 1.170833
## 3 3 6.472727 2.990909 5.183117 1.815584Comparing linkages
In the previous instance, we have used complete
linkage. For practical purposes, we may want to examine which
choice of linkages is the best one for our data set. A way to do this,
is to use the agnes function (acronym for AGglomerative
NESting) found in the cluster package. This will compute
the so called agglomerative coefficient (AC). The AC
measures the dissimilarity of an object to the first cluster it joins,
divided by the dissimilarity of the final merger in the cluster
analysis, averaged across all samples. The AC represents the strength of
the clustering structure; values closer to 1 indicates that clustering
structure is more balanced while values closer to 0 suggests less well
balanced clusters. The higher the value, the better.
library(cluster)
m <- c("average","single","complete")
names(m) <- c("average","single","complete")
# function to compute coefficient
ac <- function(x){
agnes(iris.scaled, method = x)$ac
}We can now use the map function from tidyverse package,
specifically map_dbl() to obtain the agglomerative
coefficients. Note that the map functions transform their input by
applying a function to each element of a list or atomic vector
(use Google to check the meaning of atomic vector) and
returning an object of the same length as the input.
library(tidyverse)
map_dbl(m,ac)## average single complete
## 0.9035705 0.8023794 0.9438858The highest ac value is 94.4%. So, complete linkage is
the best choice among the three. We are on course with the use of
complete linkage.
We remark that the choice of linkages can be extended to other
methods (For example hclust() allows also
centroid, ward.D, wardD.2,
median and mcquitty). These are outside the
scope of our workshop.
Other visualizations
We can also visualise the data as a fancy kind of tree using the
package igraph and combining it with the
fviz_dend() function. These trees are known in biology as
``phylogenic trees’’, then giving the name to the type option, which can
then be used for any type of data.
library(igraph)
fviz_dend(hc, k = 3, k_colors = "jco", type = "phylogenic", repel = TRUE)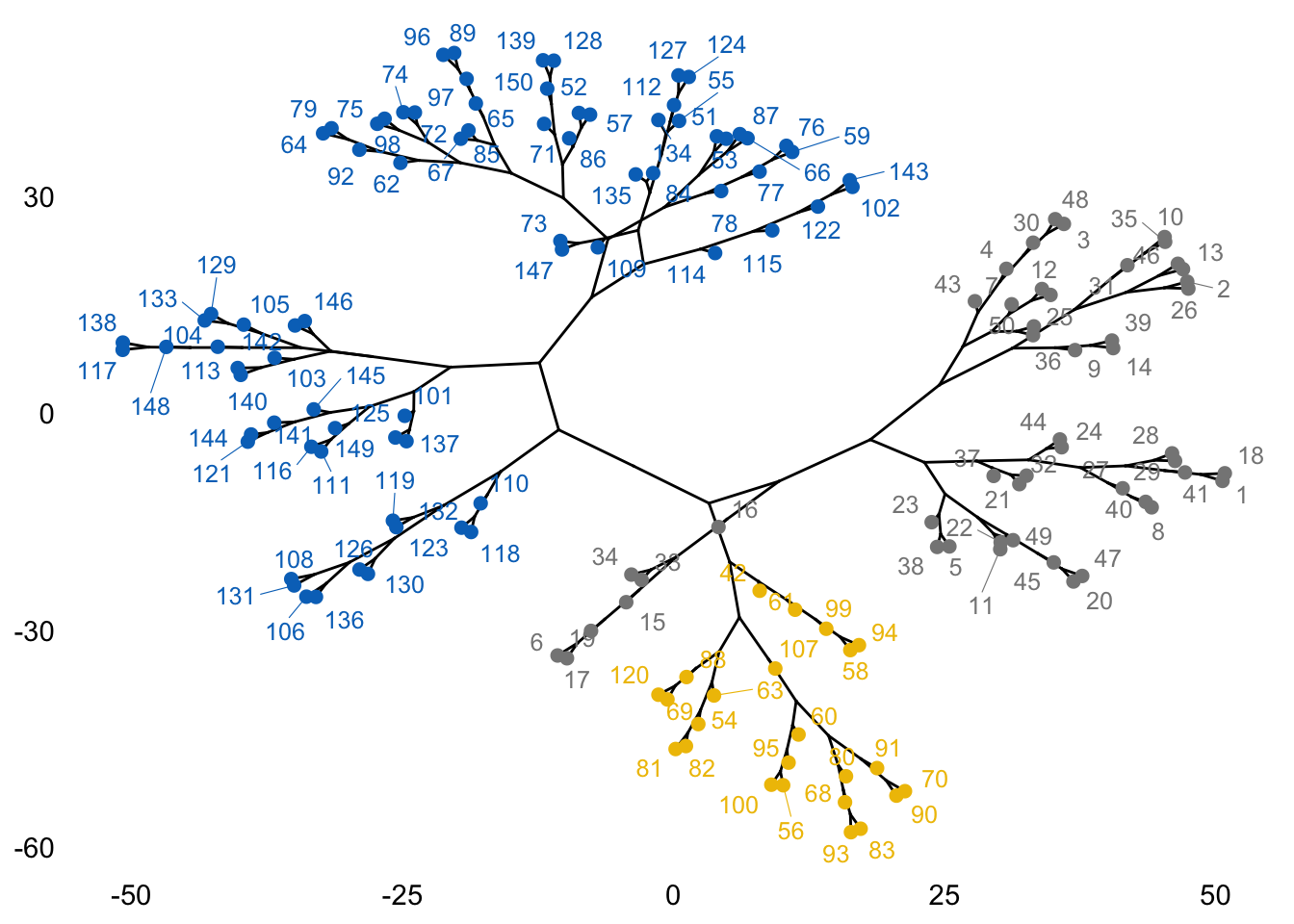
As we did for K-means and K-medoids, we can compare original species labels with our results from Hierarchical clustering:
dd <- cbind(iris, cluster=hcut)
table(dd$Species,dd$cluster)##
## 1 2 3
## setosa 49 1 0
## versicolor 0 21 29
## virginica 0 2 48Overall, a correct classification is obtained in 78.7% percent of the observations. But we can do much better! If we are willing to be more sophisticated, we can try model-based clustering.
Model-based clustering: the Gaussian mixture model
The clustering methods that we have discussed so far neither involve any
sort of model nor are based on a density estimate. Model-based
clustering considers the data as coming from a distribution that is a
mixture of two or more clusters. In the Gaussian mixture model, each
cluster \(C_k\) is modelled by a random
variable with a multivariate normal distribution \(N_p(\mu_{k}, \Sigma_{k})\). Recall that we
have:
- \(\mu_{k}:\) mean vector for the \(k\)-th cluster
- \(\Sigma_{k}:\) covariance matrix for the \(k\)-th cluster
Aside
To get a better idea of how such a distribution looks like, we can visualize the joint probability distribution in some simple cases, such as the one of 3 clusters and 2 variables. We use the data generating process code from Lab5 (with different parameters):
# Part (a) generate data:
#
K = 3 # the number of classes
n = 20 # the number of samples per class
p = 2 # the number of variables
set.seed(123)
# Create data for class 1:
X_1 = matrix( rnorm(n*p), nrow=n, ncol=p )
for( row in 1:n ){
X_1[row,] = X_1[row,] + rep( 2, p )
}
# Create data for class 2:
X_2 = matrix( rnorm(n*p), nrow=n, ncol=p )
for( row in 1:n ){
X_2[row,] = X_2[row,] + rep( -2, p )
}
# Create data for class 3:
X_3 = matrix( rnorm(n*p), nrow=n, ncol=p )
for( row in 1:n ){
X_3[row,] = X_3[row,] + c( rep( 1, p/2 ), rep( -1, p/2 ) )
}
X <- rbind(X_1, X_2, X_3)library(mclust)
ex.mc <- Mclust(X, G=3)## fitting ...
##
|
| | 0%
|
|======= | 7%
|
|============= | 13%
|
|==================== | 20%
|
|========================== | 27%
|
|================================= | 33%
|
|======================================== | 40%
|
|============================================== | 47%
|
|===================================================== | 53%
|
|=========================================================== | 60%
|
|================================================================== | 67%
|
|========================================================================= | 73%
|
|=============================================================================== | 80%
|
|====================================================================================== | 87%
|
|============================================================================================ | 93%
|
|===================================================================================================| 100%plot(ex.mc, what = "density")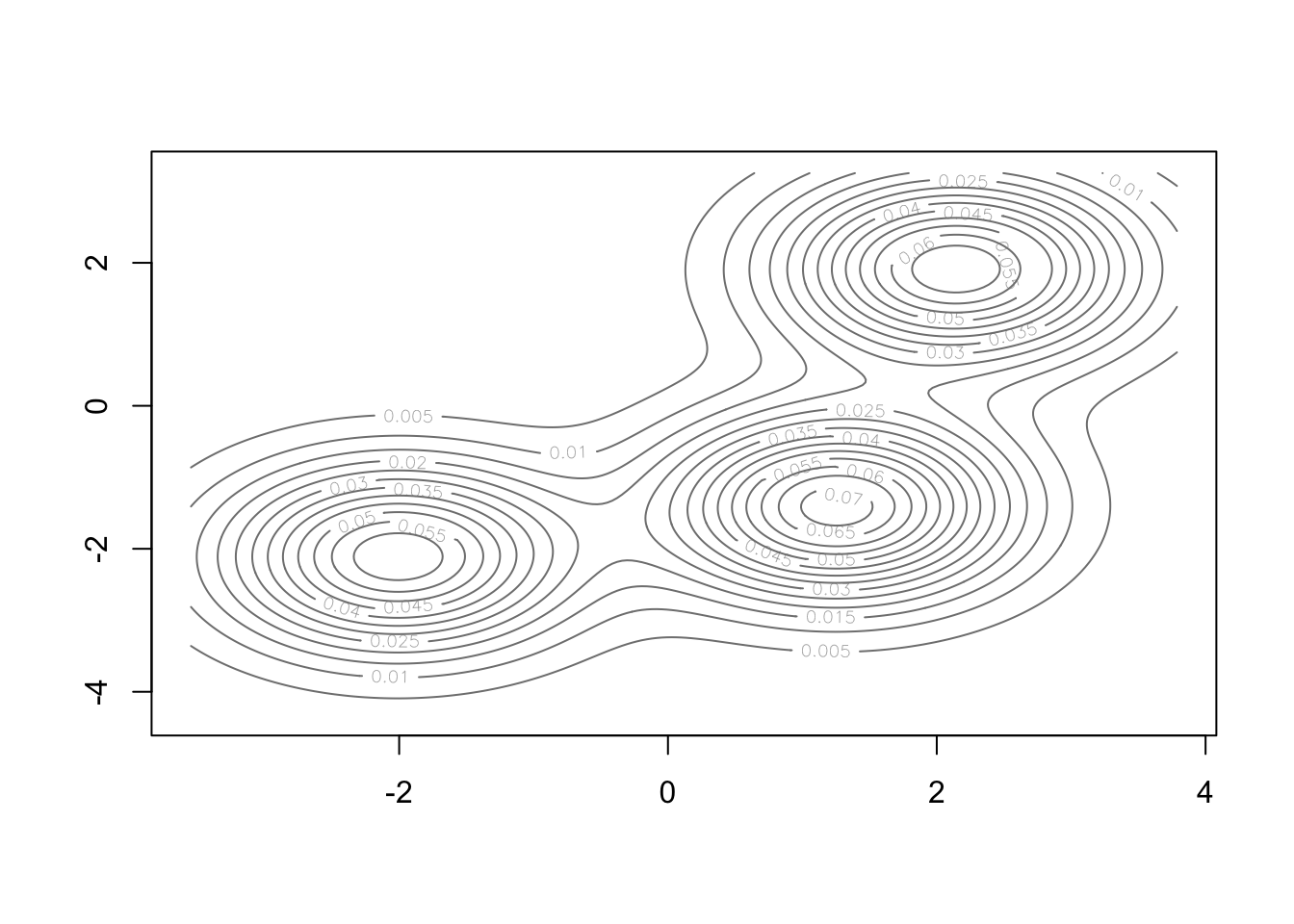
The model parameters \(\mu_{k}\) and \(\Sigma_{k}\) can be estimated using the Expectation-Maximisation (EM) algorithm. As a result, each observation point \(x\) comes with a probability of belonging to a cluster \(p_k(x)\). These probabilities satisfy
\[p_1(x)+\dots+p_n(x)=1,\] where
\(n\) is the total number of clusters,
as we are assuming that all points belong to some cluster. This method
has been implemented in the mclust package in R.
Since the model is based on maximum likelihood estimation, criteria such as BIC (Bayesian Information Criterion) and AIC (Akaike Information Criterion) can be used for the selection of the number of clusters.
We briefly recall the form of these two criteria:
\[AIC = -2logL +2p\] \[BIC = -2logL +log(n)p\] where \(logL\) is the model log-likelihood, \(p\) is the number of parameters and \(n\) is the number of observations. In general, we want these quantities to be small. The model with the smallest value of the criterion is selected as the best.
BIC is often used for selecting the number of clusters.
Let us see how good model based clustering is on the iris data set.
iris.scaled <- scale(iris[, -5]) # Standardise the data
mc <- Mclust(iris.scaled, G = 3) # Model-based-clustering, G=3 indicates a request for 3 clusters## fitting ...
##
|
| | 0%
|
|======= | 7%
|
|============= | 13%
|
|==================== | 20%
|
|========================== | 27%
|
|================================= | 33%
|
|======================================== | 40%
|
|============================================== | 47%
|
|===================================================== | 53%
|
|=========================================================== | 60%
|
|================================================================== | 67%
|
|========================================================================= | 73%
|
|=============================================================================== | 80%
|
|====================================================================================== | 87%
|
|============================================================================================ | 93%
|
|===================================================================================================| 100%summary(mc)## ----------------------------------------------------
## Gaussian finite mixture model fitted by EM algorithm
## ----------------------------------------------------
##
## Mclust VVV (ellipsoidal, varying volume, shape, and orientation) model with 3 components:
##
## log-likelihood n df BIC ICL
## -288.5255 150 44 -797.519 -800.7391
##
## Clustering table:
## 1 2 3
## 50 45 55The result indicates that there are 50 observations in cluster 1, 45 in cluster 2 and 55 in cluster 3.
We can examine the variables created within object
mc:
names(mc)## [1] "call" "data" "modelName" "n" "d" "G"
## [7] "BIC" "loglik" "df" "bic" "icl" "hypvol"
## [13] "parameters" "z" "classification" "uncertainty"The value that is of utmost importance in the object created is
classification. These are the newly created clusters.
mc$classification## [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2
## [53] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 3 2 3 2 2 2 2 3 2 2 2 2 2 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 3 3 3
## [105] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
As a small task, use the table() function in R to
compare the true class labels to the class labels obtained from
mclust. Does this result offer any improvement over the
K-means clustering results in Workshop 3?
##
## 1 2 3
## setosa 50 0 0
## versicolor 0 45 5
## virginica 0 0 50If you implemented this correctly, then Setosa is correctly classified (50 out of 50 correctly classified). 5 observations are misclassified in Versicolor (45 out of 50 correctly classified). Overall, 97% correct classification is obtained under the model-based clustering, whereas it was 88% under K-medoids and 83.3% under K-means.
You can obtain four different types of plot from the mc
object that was created.
Model-based clustering plots:
1: BIC
2: classification
3: uncertainty
4: density
We can plot the classification as follows:
plot(mc, what = "classification")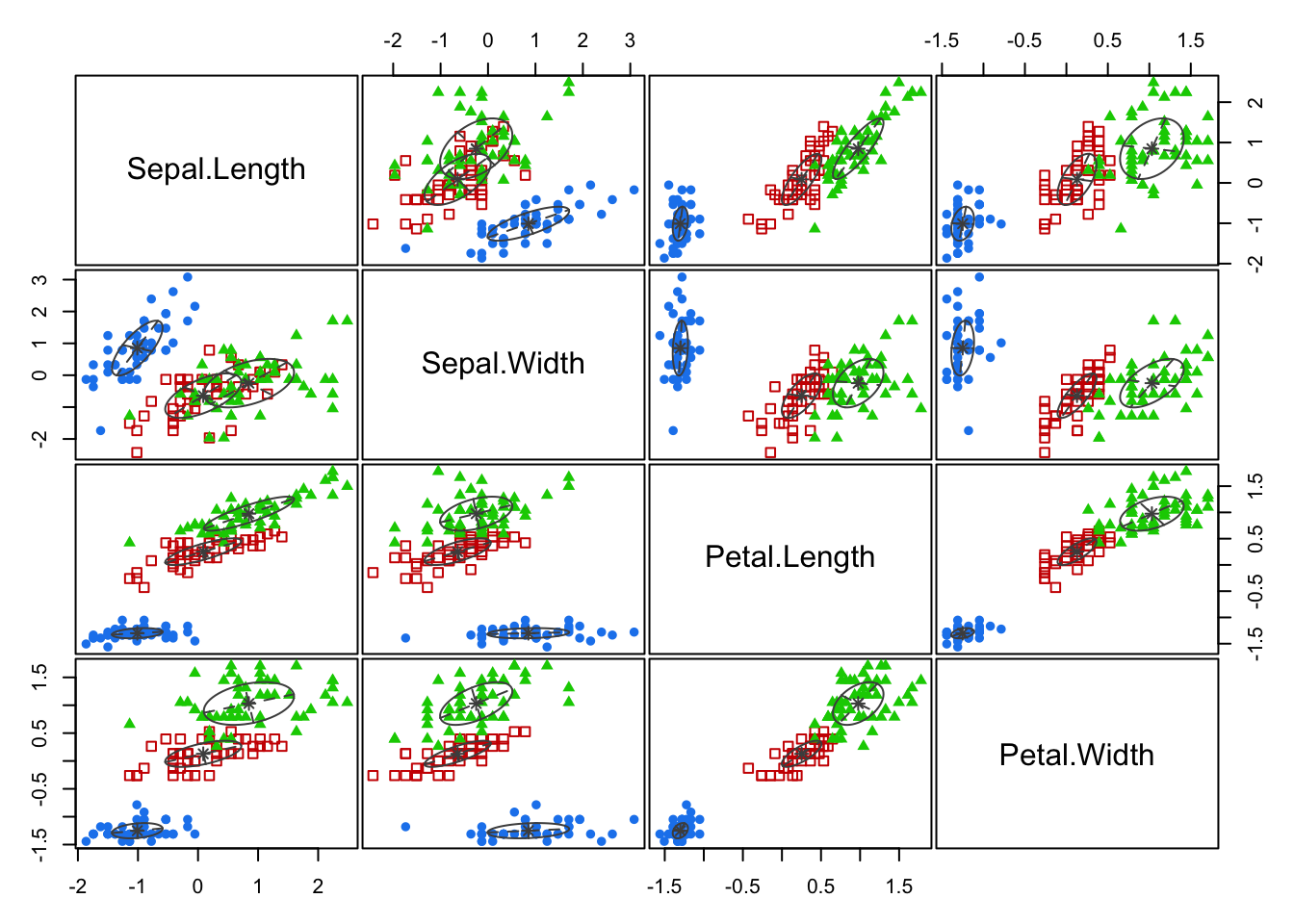
Let us compare the former plot with the one given by selecting the “uncertainty” option:
plot(mc, what = "uncertainty")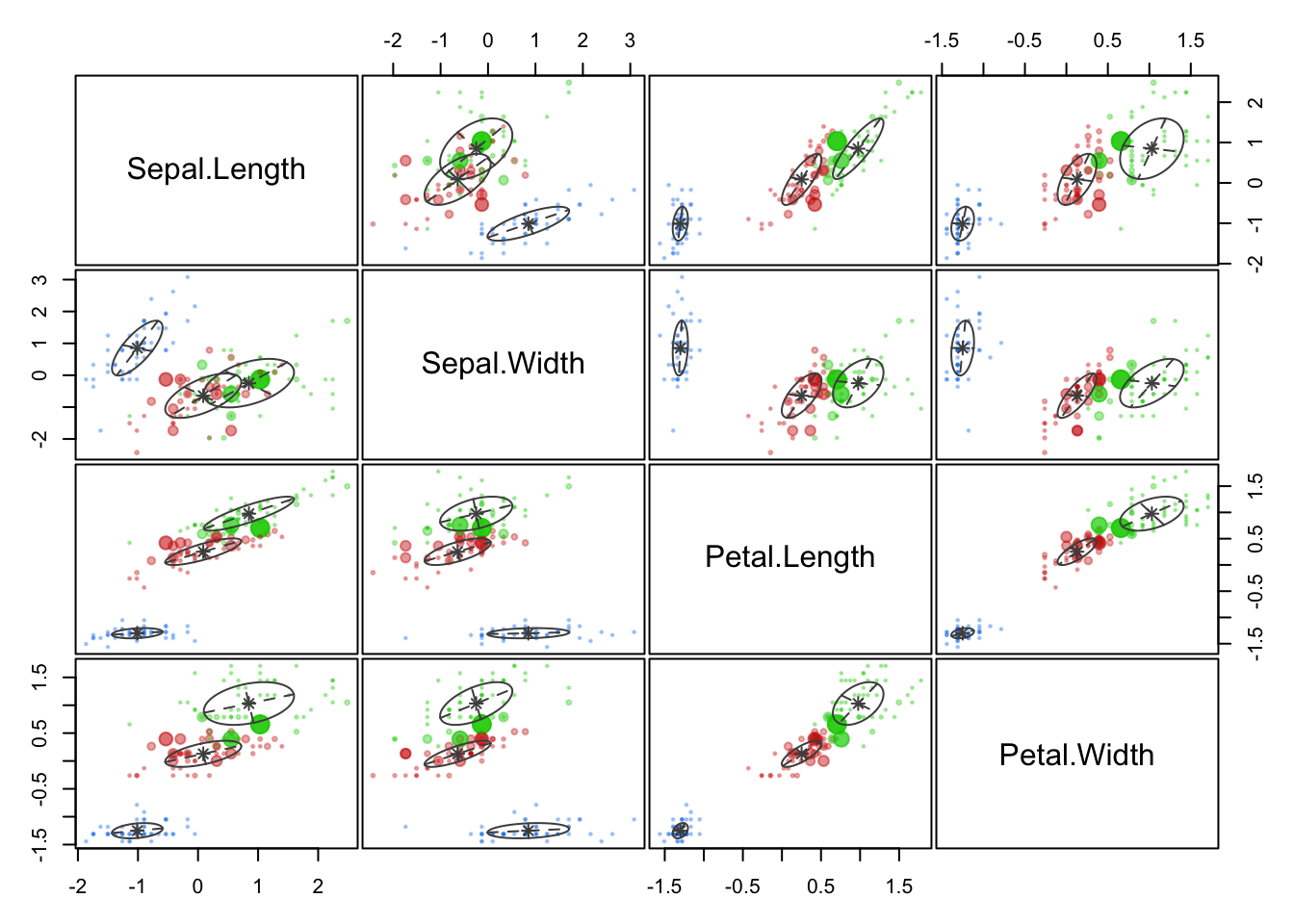
In the second one, the classification uncertainty of a point is
highlighted by the dimension of the corresponding dot.
We can identify the 5 observations that were misclassified and calculate the classification error rate as follows.
classError(mc$classification, iris[,5])## $misclassified
## [1] 69 71 73 78 84
##
## $errorRate
## [1] 0.03333333
Then, we can have a look at the plot of density functions:
plot(mc, what = "density")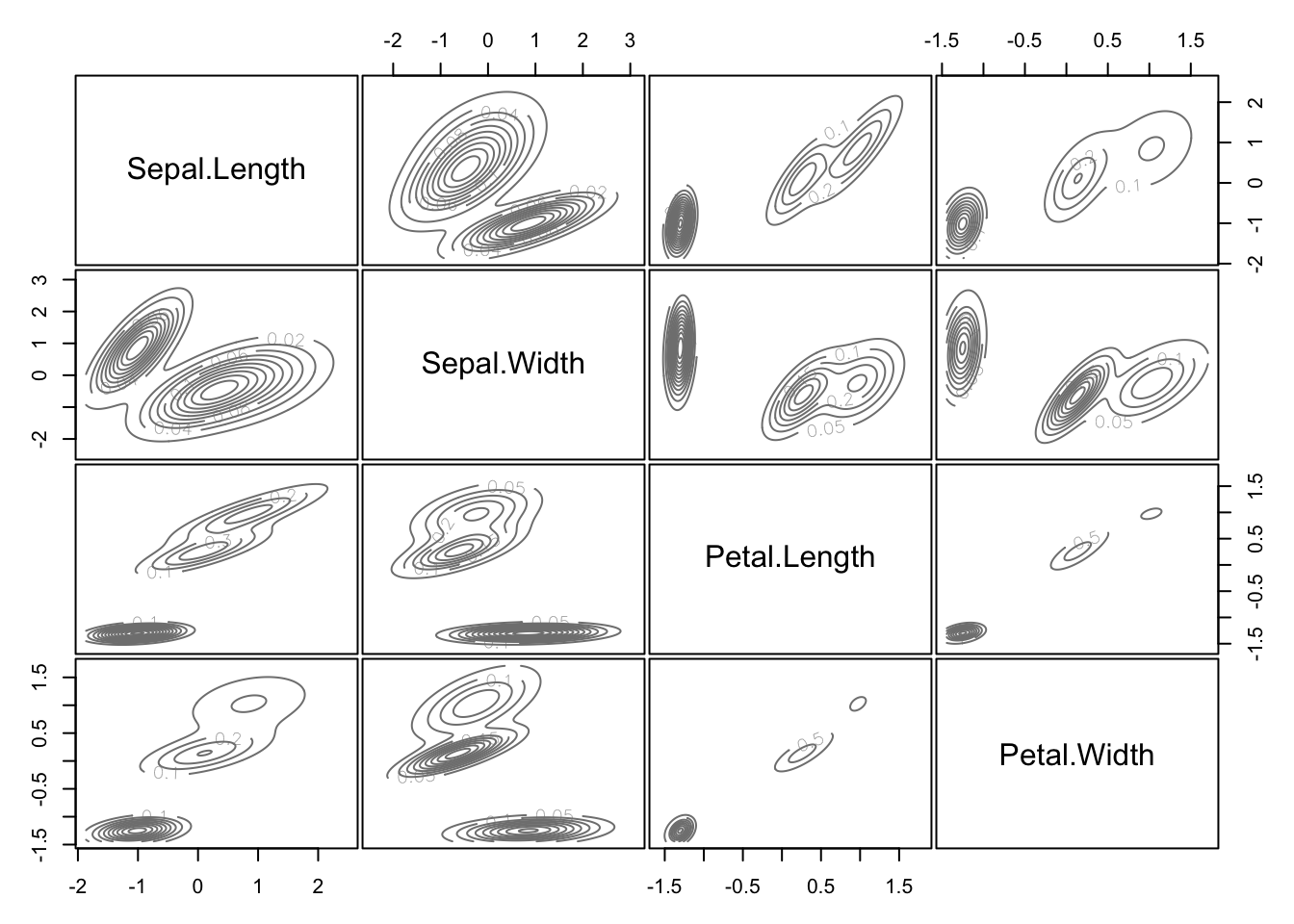 These are the probability density functions of the multivariate normals
appearing in the model.
These are the probability density functions of the multivariate normals
appearing in the model.
Finally, here is the BIC plot:
plot(mc, what = "BIC")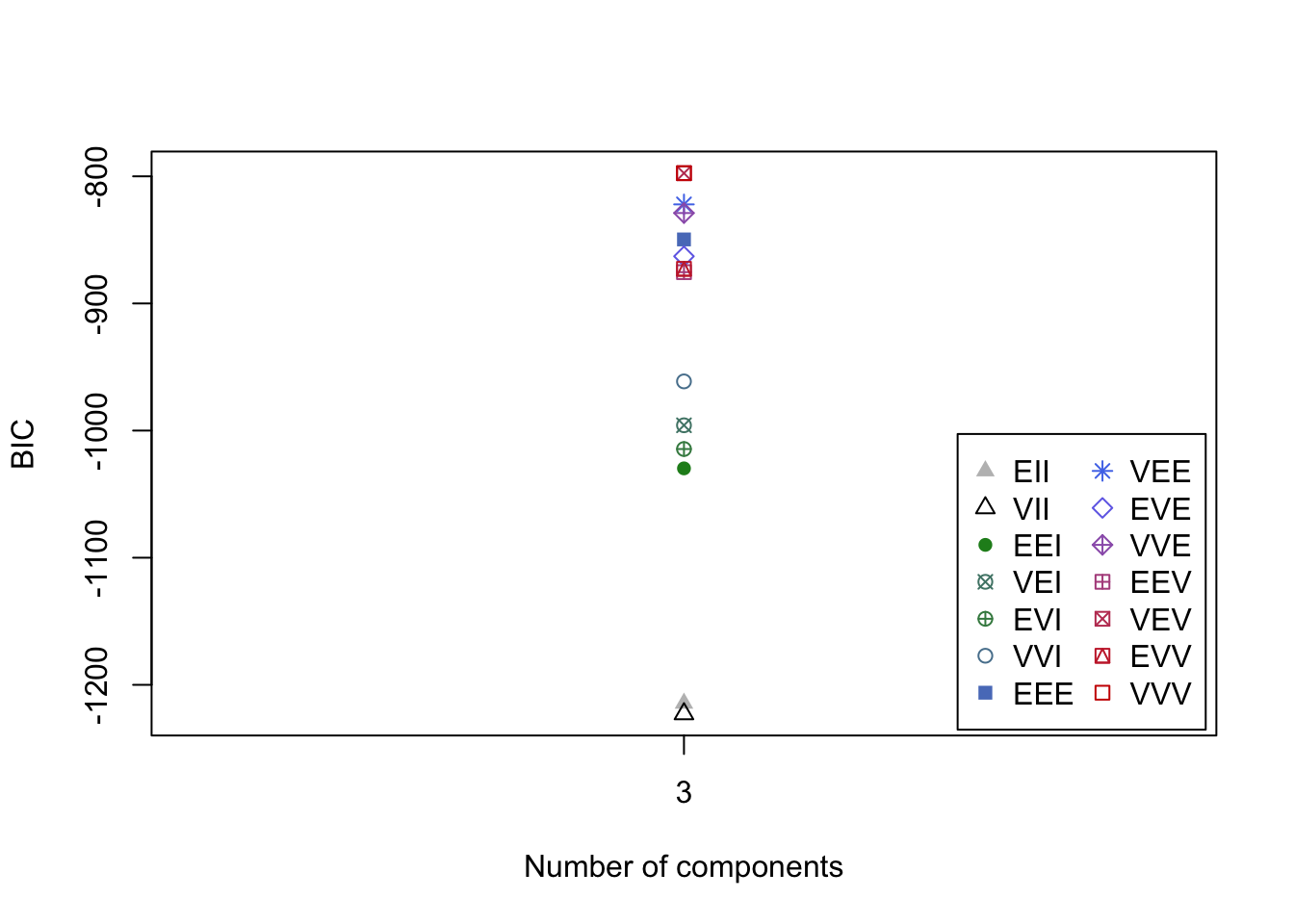
The available model options in mclust package, are
represented by identifiers including:
EII, VII, EEI, VEI, EVI, VVI, EEE, EEV, VEV and VVV. So,
VVV has been used for our example, but the plot shows that there are
different options that return a similar BIC.
What do these letters mean? The first identifier refers to volume, the second to shape and the third to orientation. E stands for “equal”, V for “variable” and I for “coordinate axes”. VEI, for example, implies that the clusters have variable volume, the same shape and orientation equal to coordinate axes. EEE means that the clusters have the same volume, shape and orientation in p-dimensional space. More on this in the Lab!
To enforce VEV as a model option, for example, you can
do the following:
mc_option <- Mclust(iris.scaled, G = 3, modelNames = "VEV")## fitting ...
##
|
| | 0%
|
|================================================== | 50%
|
|===================================================================================================| 100%Now, let us try to compare the performance of model options VEV, EVE and VEI to VVV.
You are required to fit the models using the three model options, create a classification table and compare the percentage of correct classification with what we obtained for VVV.
mc_option_VEV <- Mclust(iris.scaled, G = 3, modelNames = "VEV")## fitting ...
##
|
| | 0%
|
|================================================== | 50%
|
|===================================================================================================| 100%table(iris[,5], mc_option_VEV$classification)##
## 1 2 3
## setosa 50 0 0
## versicolor 0 0 50
## virginica 0 34 16(50+50+34)/150## [1] 0.8933333mc_option_EVE <- Mclust(iris.scaled, G = 3, modelNames = "EVE")## fitting ...
##
|
| | 0%
|
|================================================== | 50%
|
|===================================================================================================| 100%table(iris[,5], mc_option_EVE$classification)##
## 1 2 3
## setosa 50 0 0
## versicolor 0 50 0
## virginica 0 16 34(50+50+34)/150## [1] 0.8933333mc_option_VEI <- Mclust(iris.scaled, G = 3, modelNames = "VEI")## fitting ...
##
|
| | 0%
|
|================================================== | 50%
|
|===================================================================================================| 100%table(iris[,5], mc_option_VEI$classification)##
## 1 2 3
## setosa 50 0 0
## versicolor 0 48 2
## virginica 0 4 46(50+48+46)/150## [1] 0.96mc_option_VVV <- Mclust(iris.scaled, G = 3, modelNames = "VVV")## fitting ...
##
|
| | 0%
|
|================================================== | 50%
|
|===================================================================================================| 100%table(iris[,5], mc_option_VVV$classification)##
## 1 2 3
## setosa 50 0 0
## versicolor 0 45 5
## virginica 0 0 50(50+45+50)/150## [1] 0.9666667The automatically selected model option, VVV is the best
with 97% classification accuracy. This is followed by VEI
at 96% accuracy. The worst are the first two at 89.3%, although they are
still better than all the previous clustering methods (K-means,
K-medoids and Hierarchical). Unsurprisingly, model based clustering
performs much better when natural clusters are present in the data!
One should use the BIC criterion (higher values are
desirable) to select the number of clusters (G).
Consider the case below:
mc_bic <- Mclust(iris.scaled, G = 3)## fitting ...
##
|
| | 0%
|
|======= | 7%
|
|============= | 13%
|
|==================== | 20%
|
|========================== | 27%
|
|================================= | 33%
|
|======================================== | 40%
|
|============================================== | 47%
|
|===================================================== | 53%
|
|=========================================================== | 60%
|
|================================================================== | 67%
|
|========================================================================= | 73%
|
|=============================================================================== | 80%
|
|====================================================================================== | 87%
|
|============================================================================================ | 93%
|
|===================================================================================================| 100%mc_bic$BIC## Bayesian Information Criterion (BIC):
## EII VII EEI VEI EVI VVI EEE VEE EVE VVE
## 3 -1214.525 -1222.844 -1029.733 -995.8343 -1014.515 -961.3205 -849.6448 -822.076 -862.9077 -828.8731
## EEV VEV EVV VVV
## 3 -875.3724 -797.5483 -872.7515 -797.519
##
## Top 3 models based on the BIC criterion:
## VVV,3 VEV,3 VEE,3
## -797.5190 -797.5483 -822.0760You will observe that the results included the top 3 model options based on the BIC criterion. In fact, if no number of clusters is specified, the algorithm naturally selects the best options using BIC. The downside of this method is that it takes much longer to run:
mc_bic <- Mclust(iris.scaled)## fitting ...
##
|
| | 0%
|
|= | 1%
|
|== | 2%
|
|=== | 3%
|
|==== | 4%
|
|===== | 5%
|
|===== | 6%
|
|====== | 6%
|
|======= | 7%
|
|======== | 8%
|
|========= | 9%
|
|========== | 10%
|
|=========== | 11%
|
|============ | 12%
|
|============ | 13%
|
|============= | 13%
|
|============== | 14%
|
|=============== | 15%
|
|================ | 16%
|
|================ | 17%
|
|================= | 17%
|
|================== | 18%
|
|=================== | 19%
|
|=================== | 20%
|
|==================== | 20%
|
|===================== | 21%
|
|====================== | 22%
|
|======================= | 23%
|
|======================= | 24%
|
|======================== | 24%
|
|========================= | 25%
|
|========================== | 26%
|
|=========================== | 27%
|
|=========================== | 28%
|
|============================ | 28%
|
|============================= | 29%
|
|============================== | 30%
|
|============================== | 31%
|
|=============================== | 31%
|
|================================ | 32%
|
|================================= | 33%
|
|================================== | 34%
|
|================================== | 35%
|
|=================================== | 35%
|
|==================================== | 36%
|
|===================================== | 37%
|
|===================================== | 38%
|
|====================================== | 39%
|
|======================================= | 39%
|
|======================================== | 40%
|
|========================================= | 41%
|
|========================================= | 42%
|
|========================================== | 43%
|
|=========================================== | 43%
|
|============================================ | 44%
|
|============================================ | 45%
|
|============================================= | 46%
|
|============================================== | 46%
|
|=============================================== | 47%
|
|================================================ | 48%
|
|================================================ | 49%
|
|================================================= | 50%
|
|================================================== | 50%
|
|=================================================== | 51%
|
|=================================================== | 52%
|
|==================================================== | 53%
|
|===================================================== | 54%
|
|====================================================== | 54%
|
|======================================================= | 55%
|
|======================================================= | 56%
|
|======================================================== | 57%
|
|========================================================= | 57%
|
|========================================================== | 58%
|
|========================================================== | 59%
|
|=========================================================== | 60%
|
|============================================================ | 61%
|
|============================================================= | 61%
|
|============================================================== | 62%
|
|============================================================== | 63%
|
|=============================================================== | 64%
|
|================================================================ | 65%
|
|================================================================= | 65%
|
|================================================================= | 66%
|
|================================================================== | 67%
|
|=================================================================== | 68%
|
|==================================================================== | 69%
|
|===================================================================== | 69%
|
|===================================================================== | 70%
|
|====================================================================== | 71%
|
|======================================================================= | 72%
|
|======================================================================== | 72%
|
|======================================================================== | 73%
|
|========================================================================= | 74%
|
|========================================================================== | 75%
|
|=========================================================================== | 76%
|
|============================================================================ | 76%
|
|============================================================================ | 77%
|
|============================================================================= | 78%
|
|============================================================================== | 79%
|
|=============================================================================== | 80%
|
|================================================================================ | 80%
|
|================================================================================ | 81%
|
|================================================================================= | 82%
|
|================================================================================== | 83%
|
|=================================================================================== | 83%
|
|=================================================================================== | 84%
|
|==================================================================================== | 85%
|
|===================================================================================== | 86%
|
|====================================================================================== | 87%
|
|======================================================================================= | 87%
|
|======================================================================================= | 88%
|
|======================================================================================== | 89%
|
|========================================================================================= | 90%
|
|========================================================================================== | 91%
|
|=========================================================================================== | 92%
|
|============================================================================================ | 93%
|
|============================================================================================= | 94%
|
|============================================================================================== | 94%
|
|============================================================================================== | 95%
|
|=============================================================================================== | 96%
|
|================================================================================================ | 97%
|
|================================================================================================= | 98%
|
|================================================================================================== | 99%
|
|===================================================================================================| 100%mc_bic$BIC## Bayesian Information Criterion (BIC):
## EII VII EEI VEI EVI VVI EEE VEE EVE
## 1 -1723.766 -1723.766 -1738.7979 -1738.7979 -1738.7979 -1738.7979 -1046.6559 -1046.6559 -1046.6559
## 2 -1344.053 -1325.273 -1259.6457 -1172.9600 -1223.9860 -1074.2293 -904.7750 -873.0048 -906.9282
## 3 -1214.525 -1222.844 -1029.7330 -995.8343 -1014.5146 -961.3205 -849.6448 -822.0760 -862.9077
## 4 -1177.163 -1139.392 -1044.1118 -965.1348 -1054.2229 -967.7021 -862.7323 -821.5149 -902.9964
## 5 -1135.642 -1107.791 -958.6219 -905.0241 -983.5054 -928.1301 -821.5159 NA -901.9539
## 6 -1131.245 -1102.864 -910.4787 -892.8517 -990.7497 -923.9756 -826.5558 -826.2392 -873.0654
## 7 -1119.876 -1053.274 -929.8709 -897.4180 -1030.2038 -983.3316 -849.1854 NA -913.1458
## 8 -1124.299 -1059.090 -908.1008 -896.1450 -957.1355 -980.8747 -855.9594 -871.9319 -934.3770
## 9 -1114.899 -1060.444 -912.9422 -918.7055 -984.5159 -972.5093 -869.7734 NA -955.8249
## VVE EEV VEV EVV VVV
## 1 -1046.6559 -1046.6559 -1046.6559 -1046.6559 -1046.6559
## 2 -880.7933 -873.6590 -802.5253 -875.0084 -790.6956
## 3 -828.8731 -875.3724 -797.5483 -872.7515 -797.5190
## 4 -881.1270 -930.1693 -821.4057 -941.9898 -847.2777
## 5 -853.4148 -877.2201 -837.6111 NA -893.2973
## 6 -865.1217 -905.4942 -879.2801 NA -971.4786
## 7 -898.7411 -953.7660 -920.8553 -1026.5234 -1023.6106
## 8 -908.8799 -955.7741 -939.3449 -1048.4311 -1047.3167
## 9 -947.9984 -990.5646 -987.1010 -1099.1226 -1100.3729
##
## Top 3 models based on the BIC criterion:
## VVV,2 VVV,3 VEV,3
## -790.6956 -797.5190 -797.5483In summary: model-based clustering allows for mixing between clusters, it is useful to give precise metrics of mis-clustering (hence easier to manage outliers), and more flexibility as we are assigning a probability rather than a certainty.