• Visualising multivatiate categorical data using:
    • Stacked barplots for small problems
    • doubledecker and mosaicplot for larger problems

You will need to install the following packages for today’s workshop:

  • vcd for the doubledecker functions
install.packages("vcd")

1 Multivariate categorical data

Displaying combinations of categorical variables can be quite difficult, as we can’t represent our data as simple points in a space. Instead, we summarise a categorical variable (e.g. eye colour) with multiple levels (blue, green, brown, …) by the frequencies of each of the levels in the data. When we have multiple categorical variables, we work instead with the counts of the combinations of the levels (e.g. red hair + green eyes).

All of our plots are some sort of visualisation of these counts and so are (in one way or another) variations and manipulations of stacked barplots. Multivariate categorical data is a little more complex to work with, so generally it is recommended to start with single or pairs of variables and progressively add more, rather than visualising everything all at once like a scatterplot matrix.

Download data: arthritis

The arthritis data contains the results from a double-blind clinical trial investigating a new treatment for rheumatoid arthritis. The variables are:

  • ID - patient ID.
  • Treatment - factor indicating treatment (Placebo, Treated).
  • Sex - factor indicating sex (Female, Male).
  • Age - age of patient.
  • Improved - ordered factor indicating treatment outcome (None, Some, Marked).

Treatment, Sex, and Improved are all categorical variables. Improved is also ordinal, since the category levels can be ordered. The question is whether the patient improvement depends on the Treatment and Sex.

First, let’s have a quick look at the data.

head(arthritis)
ID Treatment Sex Age Improved
57 Treated Male 27 Some
46 Treated Male 29 None
77 Treated Male 30 None
17 Treated Male 32 Marked
36 Treated Male 46 Marked
23 Treated Male 58 Marked

Note that each row in the data is an individual patient, rather than summaries of the counts of the different category combinations.

1.1 Mosaic plots

Mosaic plots can display the relationship between categorical variables using rectangular tiles, whose areas represent the proportion of cases for any given combination of levels. A mosaic plot of a single variable is basically a simple stacked barplot with only one bar. Looking at the patient improvement only, we see

mosaicplot(~Improved, data=arthritis,col=2:4,main='')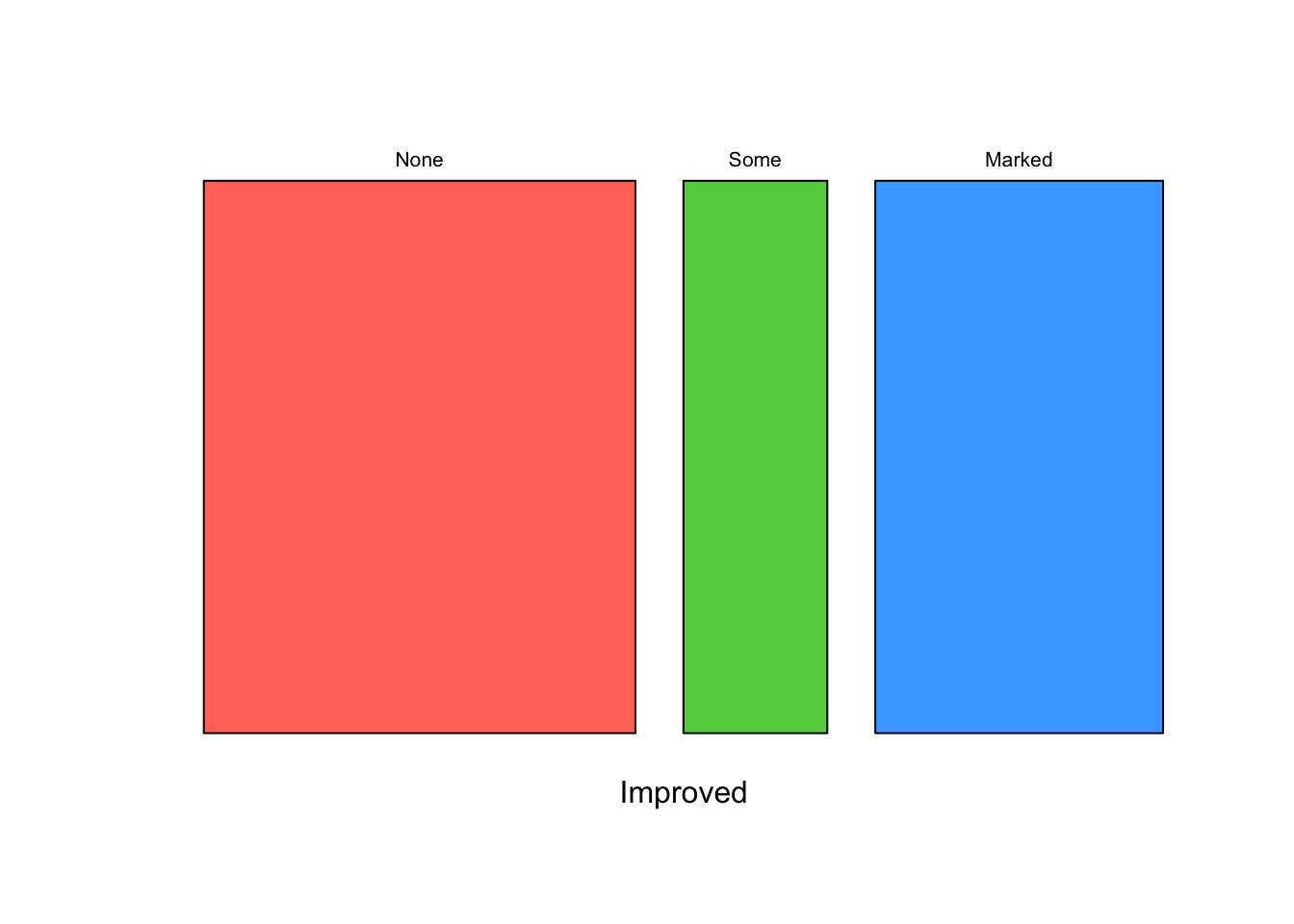

Since the None box is largest, we see that this appears to be the most common patient outcome. But taking the Some and Marked improvements together, it’s actually an even split. Let’s see how this depends on what Treatment the patient received - we would hope to see more improvement from those in the Treated group:

mosaicplot(~Treatment+Improved, data=arthritis,col=2:4,main='')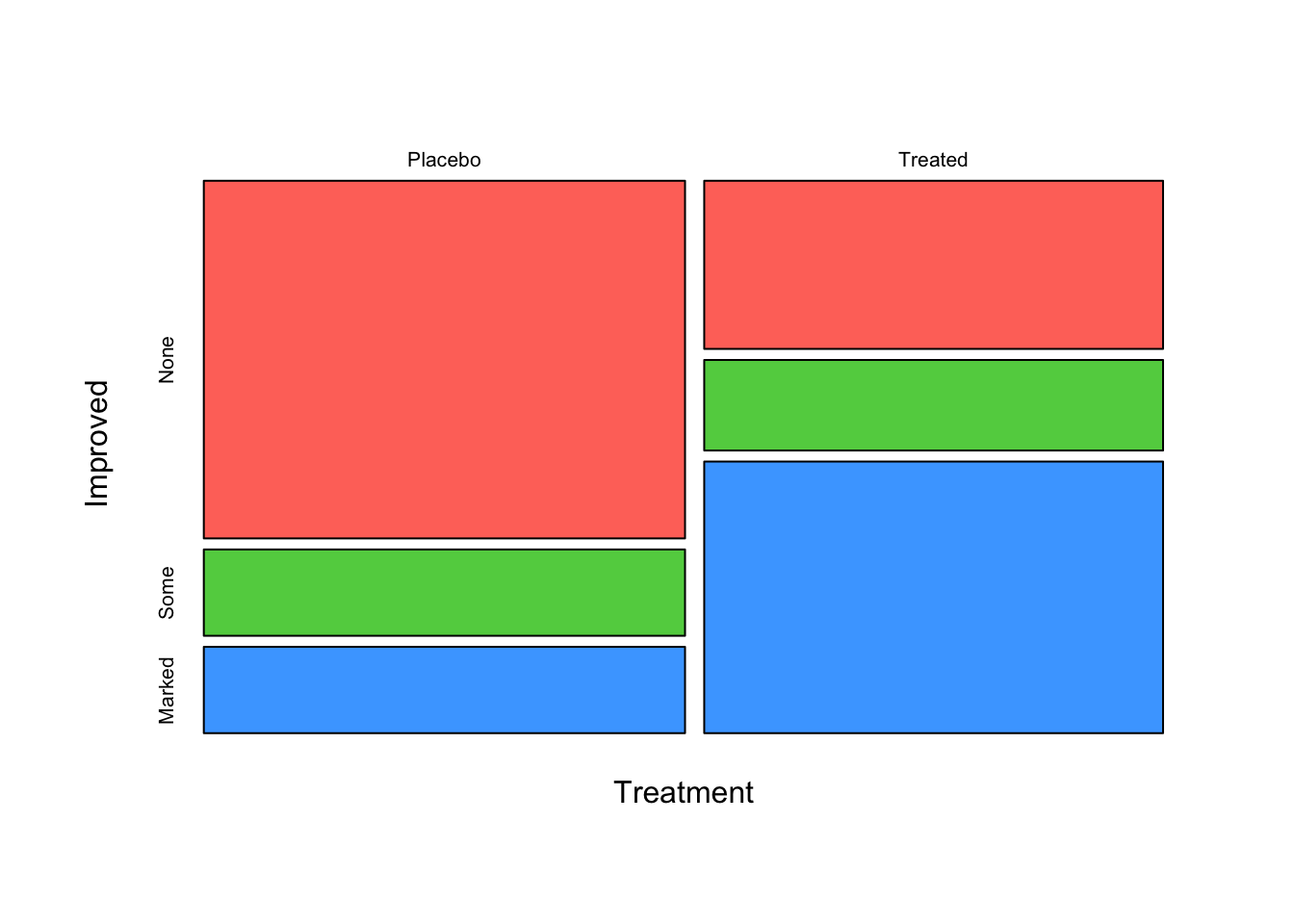

Note that the plot now has two splits: the first split is horizontal into bars for the “Treated” and “Placebo” groups, while the second set of splits divides each bar up into the different Improved categories. If Treatment had no effect on the Improved state, then we would see a regular grid where the two sets of bars would have splits of approximately the same size and we could draw lines from the left of the plot to the right without cutting through any of the tiles.

However, we can see clearly that a greater proportion of patients improved on treatment than in the placebo group and so the distribution of Improved is different for different values of Treatment, which may point towards an association between these variables and maybe hints at treatment being effective!

If we reverse the positions of Improved and Treatment in the function, it change the order in which the bars are split:

mosaicplot(~Improved+Treatment, data=arthritis, col=2:4,main='')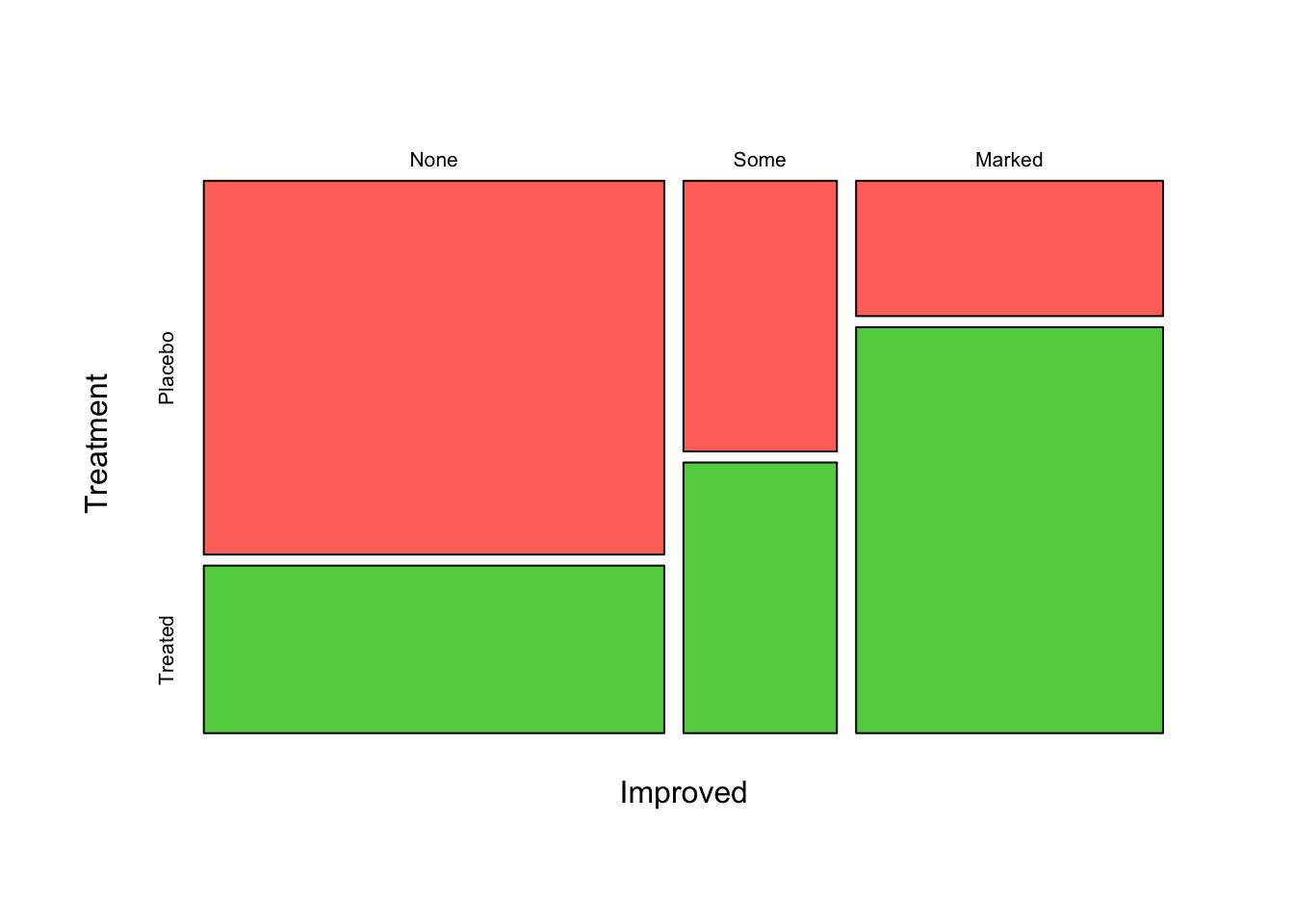

Now we have three vertical bars for Improved, each sub-divided into the Treatment groups. This plot now shows how the patients with different Improved levels break down into the Treatment groups. So, we would read this as saying for those patients with a Marked improvement, the majority were Treated rather than given Placebo. Usually, it is best to split on the response variable at the end, as we had done in the previous plot.

1.2 More variables

We can continue to add variables to the plot and break down the results into more groups. For instance, we can introduce Sex as a variable

mosaicplot(~Treatment+Sex+Improved, data=arthritis,col=2:4,main='')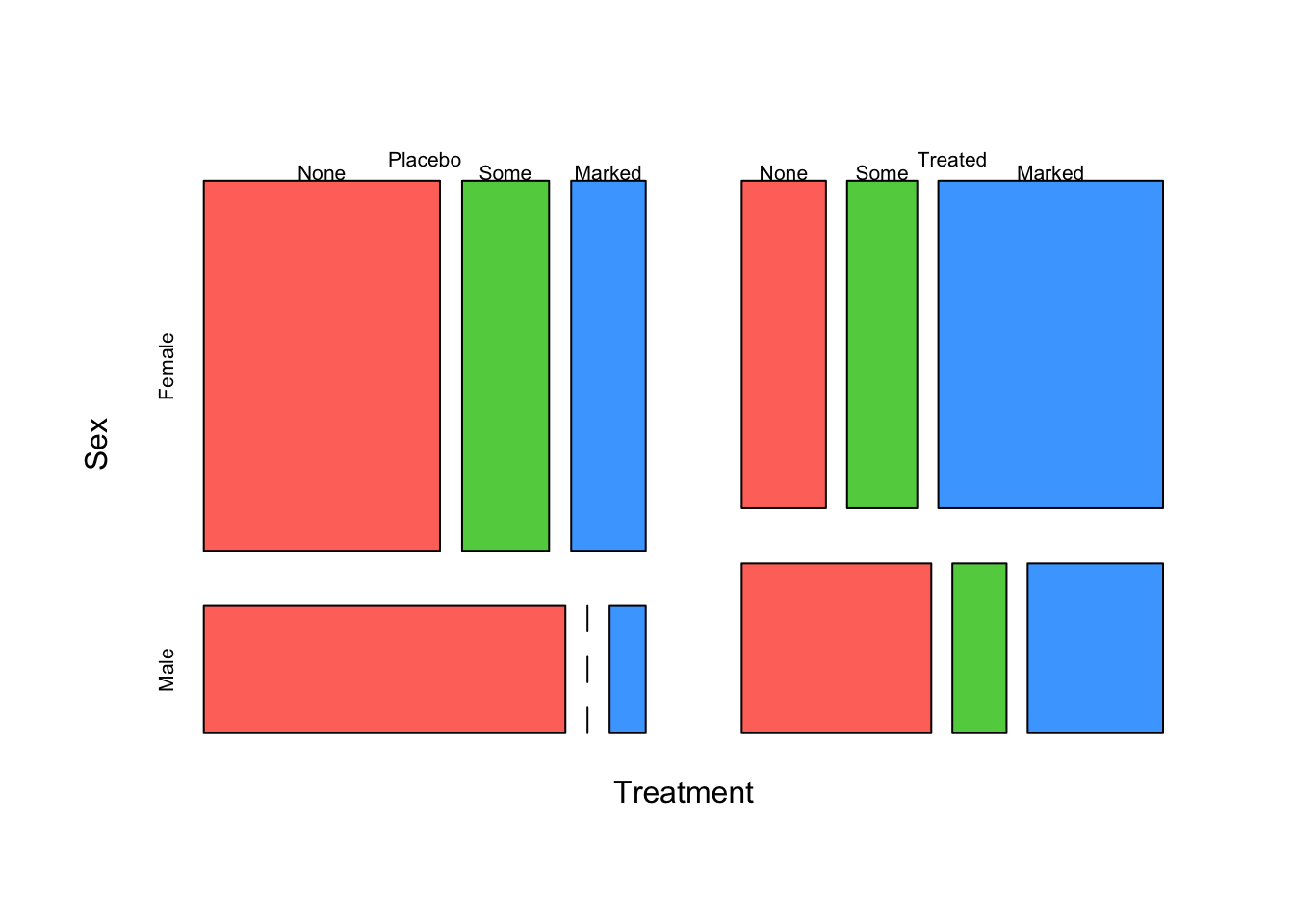

Here we can see:

  • The Treatment groups look to be roughly equal in size
  • There are fewer men than women in the study (the Male rows are narrower than the Female)
  • There are no Male patients in the Placebo group who only had Some improvement - this is indicated by the dashed line where this bar should be.
  • Treatment appears to have a positive effect
  • Female patients seemed to improve the most in general, and particularly under Treatment

It is often worth reordering the variables in the mosaic plot formula to see if a different sequence of splits is a more effective visualisation for your problem. Generally, our dependent variable of interest is split last following the ~ in the function call.

  • Experiment with the ordering of the variables in the call to the mosaicplot function to see how different orderings produce different presentations of the data. 
## there are 3!=6 different orderings - here are a couple
mosaicplot(~Improved+Sex+Treatment, data=arthritis,col=2:4,main='')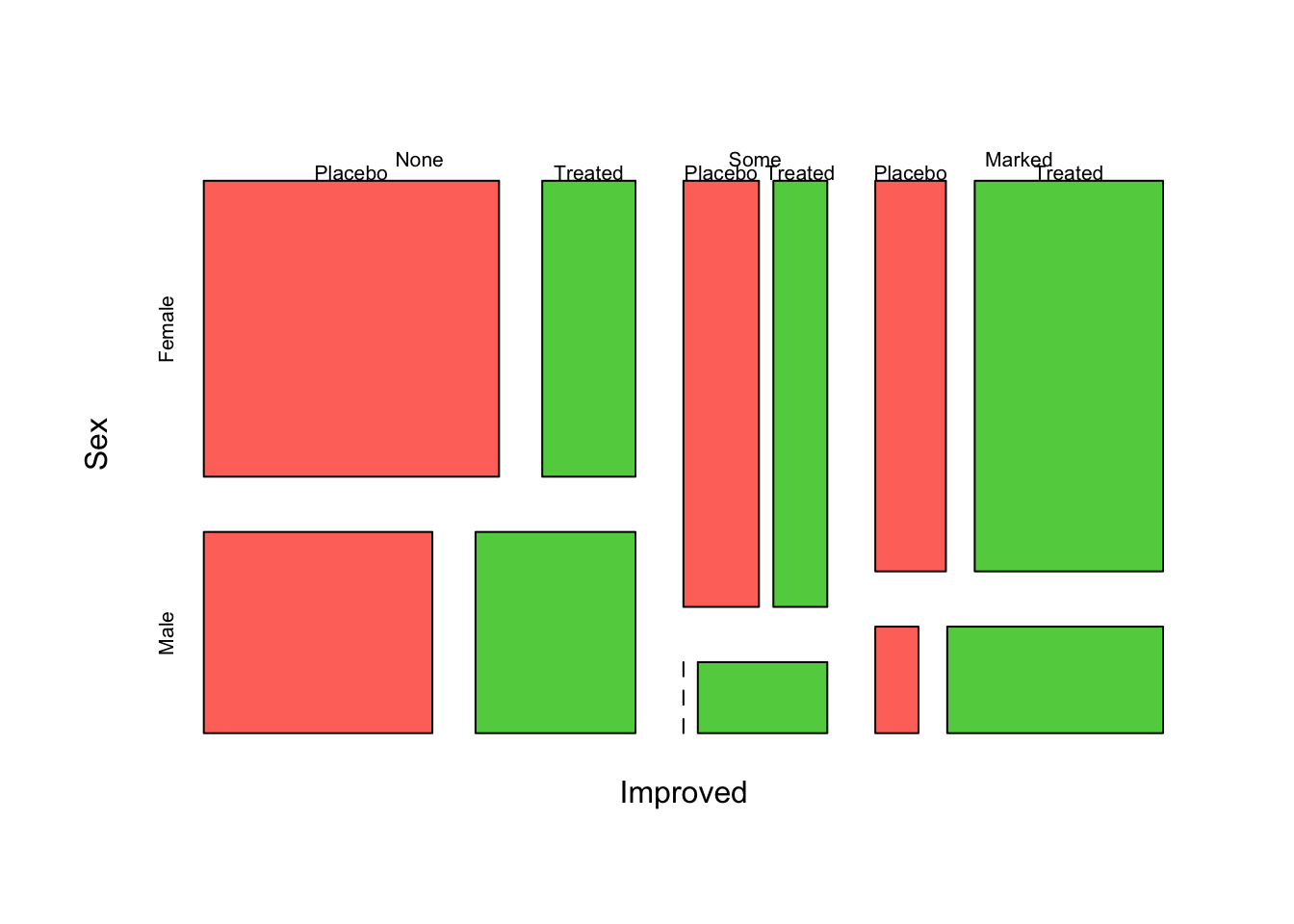

mosaicplot(~Sex+Improved+Treatment, data=arthritis,col=2:4,main='')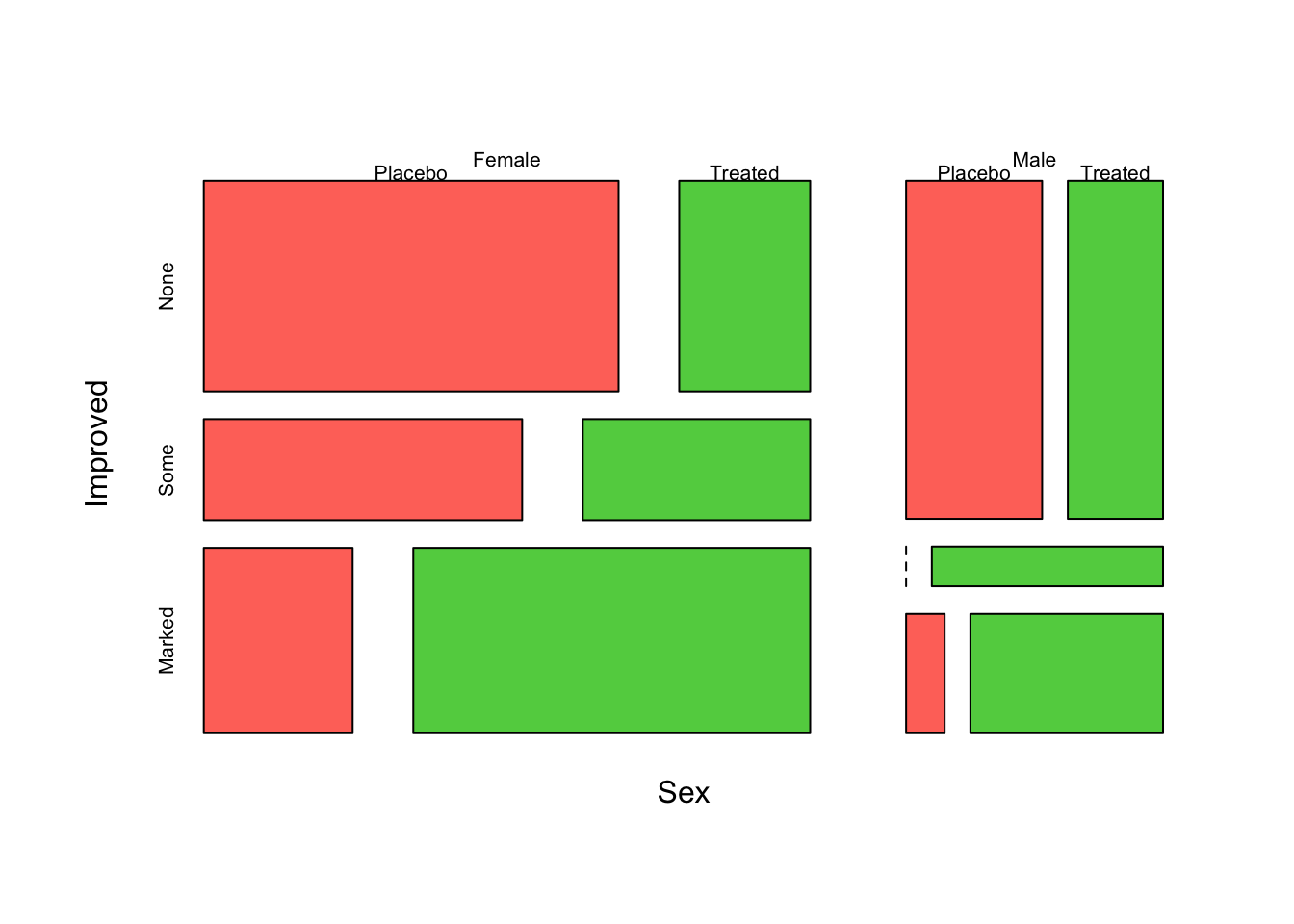

1.2.1 Directions of the splits

Note that in the previous example, the mosaic plot divides the plot using different directions depending on the order the variables are specified:

  • Treatment - first split, vertical
  • Sex - second split, horizontal
  • Improved - final split, vertical

A doubledecker plot is a version of a mosiac plot where all of the splits in the data are vertical, except for the last one. This effectively produces a type of stacked barplot, which we can achieve by setting the direction argument as follows:

mosaicplot(~Treatment+Sex+Improved, data=arthritis, dir = c("v", "v", "h"),col=2:4)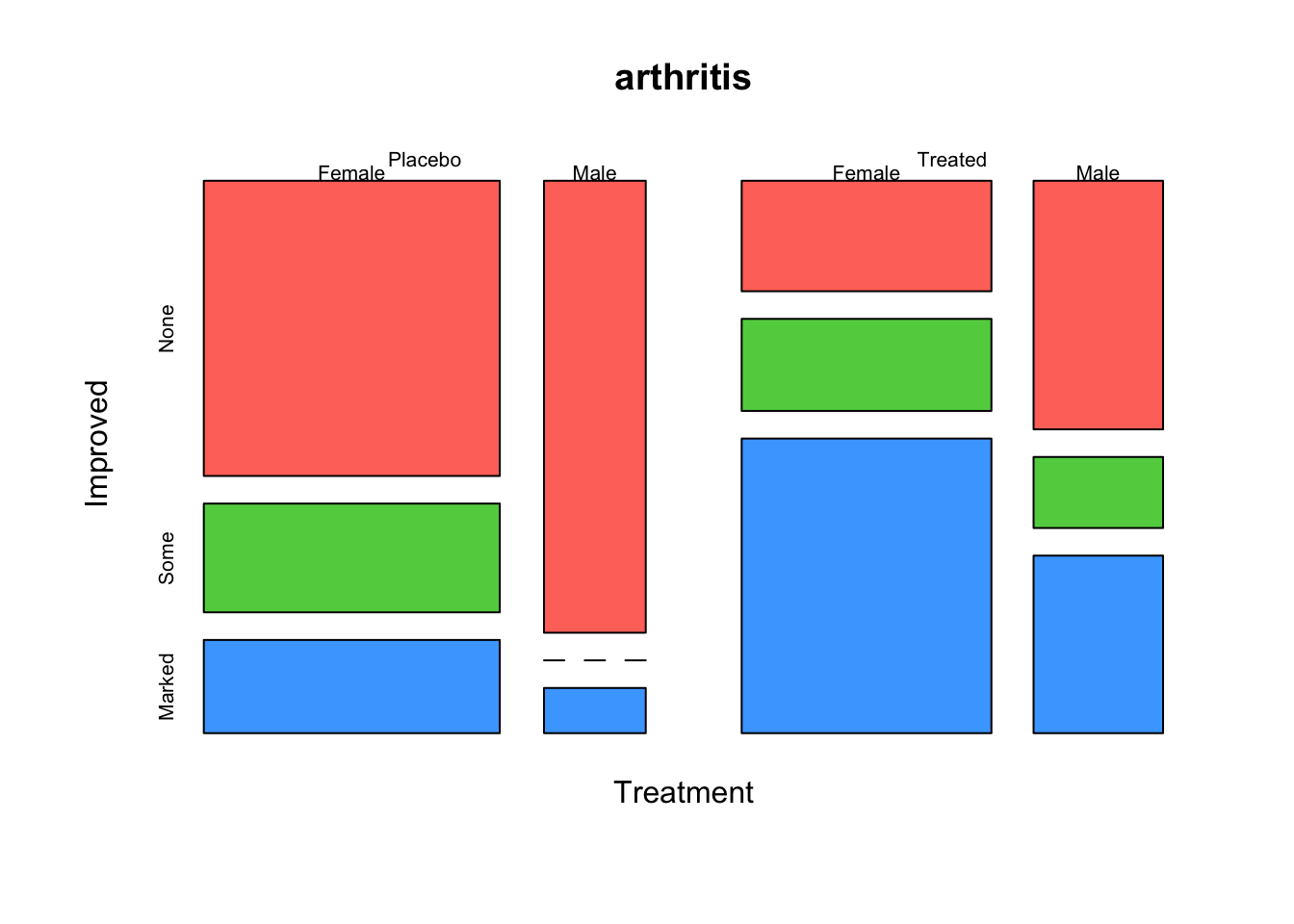

Or, using the doubledecker function directly gives an almost identical plot:

doubledecker(Improved~Treatment+Sex, data=arthritis)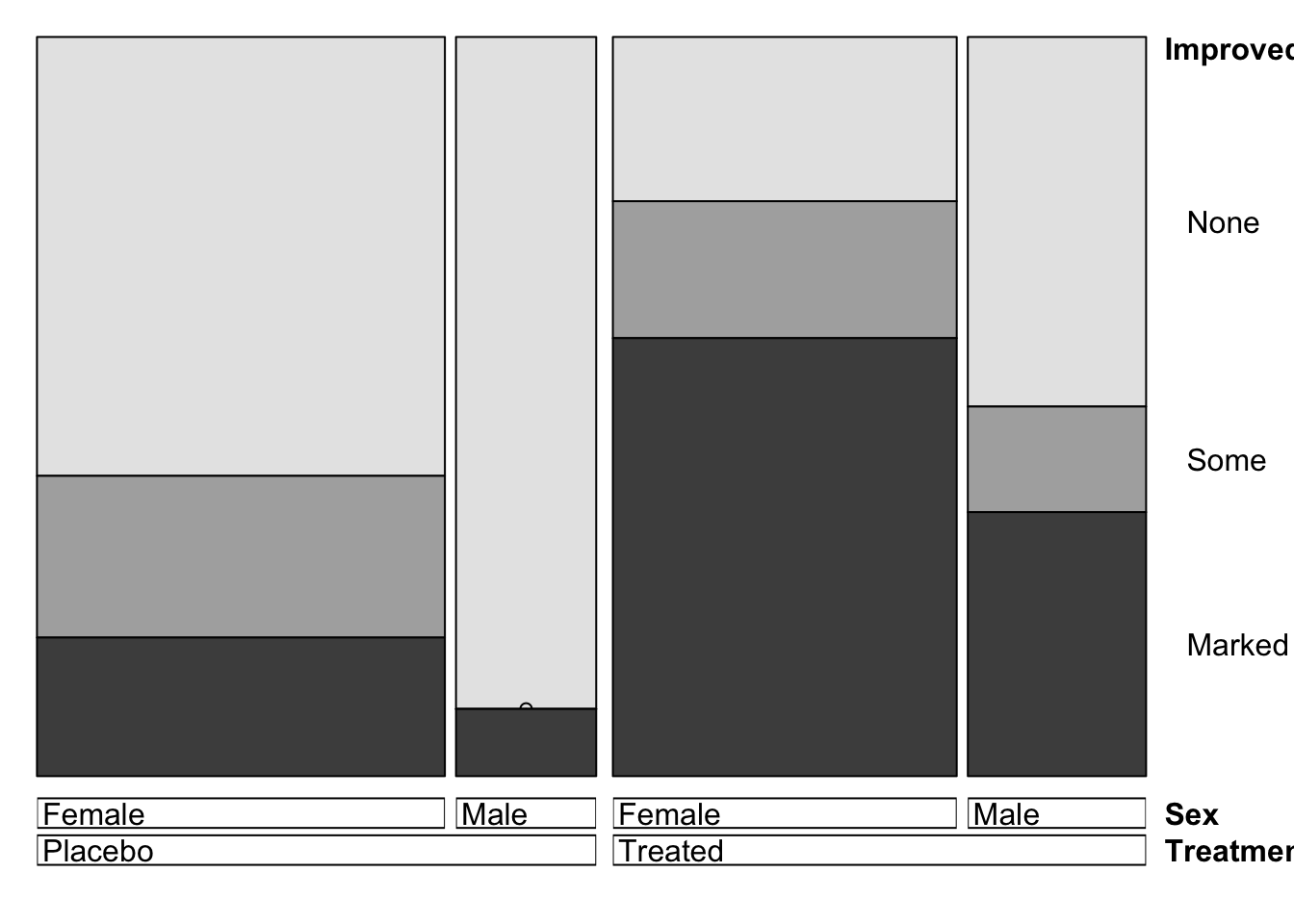

1.2.2 Adding some colour

The default plots are somewhat dull and monochrome. Note that the different shadings used in the plot correspond to the different levels of the last cut variable, i.e. the dependent variable which is Improved here. So, if we supply one colour for each level of that variable we get the following plot:

mosaicplot(~Treatment+Sex+Improved, data=arthritis, main='', col=c("wheat", "cornflowerblue", "tomato1"))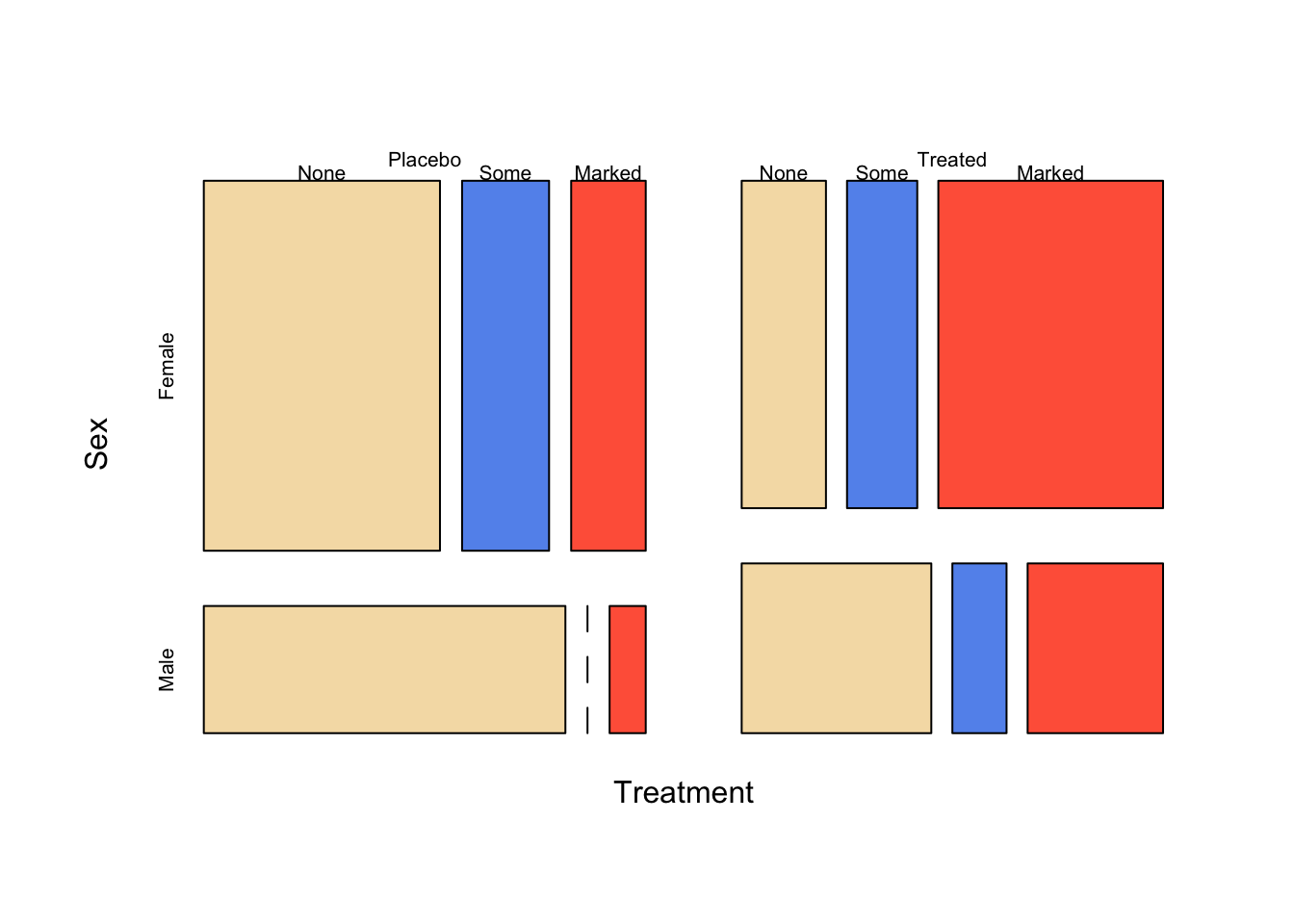

Note: In general, setting colours on mosaic plots can be quite fiddly. We won’t make much use of it, apart from an automatic coloring technique that we describe below.

1.3 Using colour to highlight unexpected patterns

A different but helpful use of colour is the shade=TRUE option. There is a formal statistical test to assess if two (or more) categorical variables are independent (i.e. have no association). This test works by comparing our observed data with what we would expect to see from a similar problem under this independence hypothesis. The shade=TRUE option works by colouring any tiles in the mosaic that are in disagreement with that hypothesis. This can help us identify any combinations that are unusually common or rate:

mosaicplot(~Treatment+Sex+Improved, data=arthritis,shade=TRUE,main='')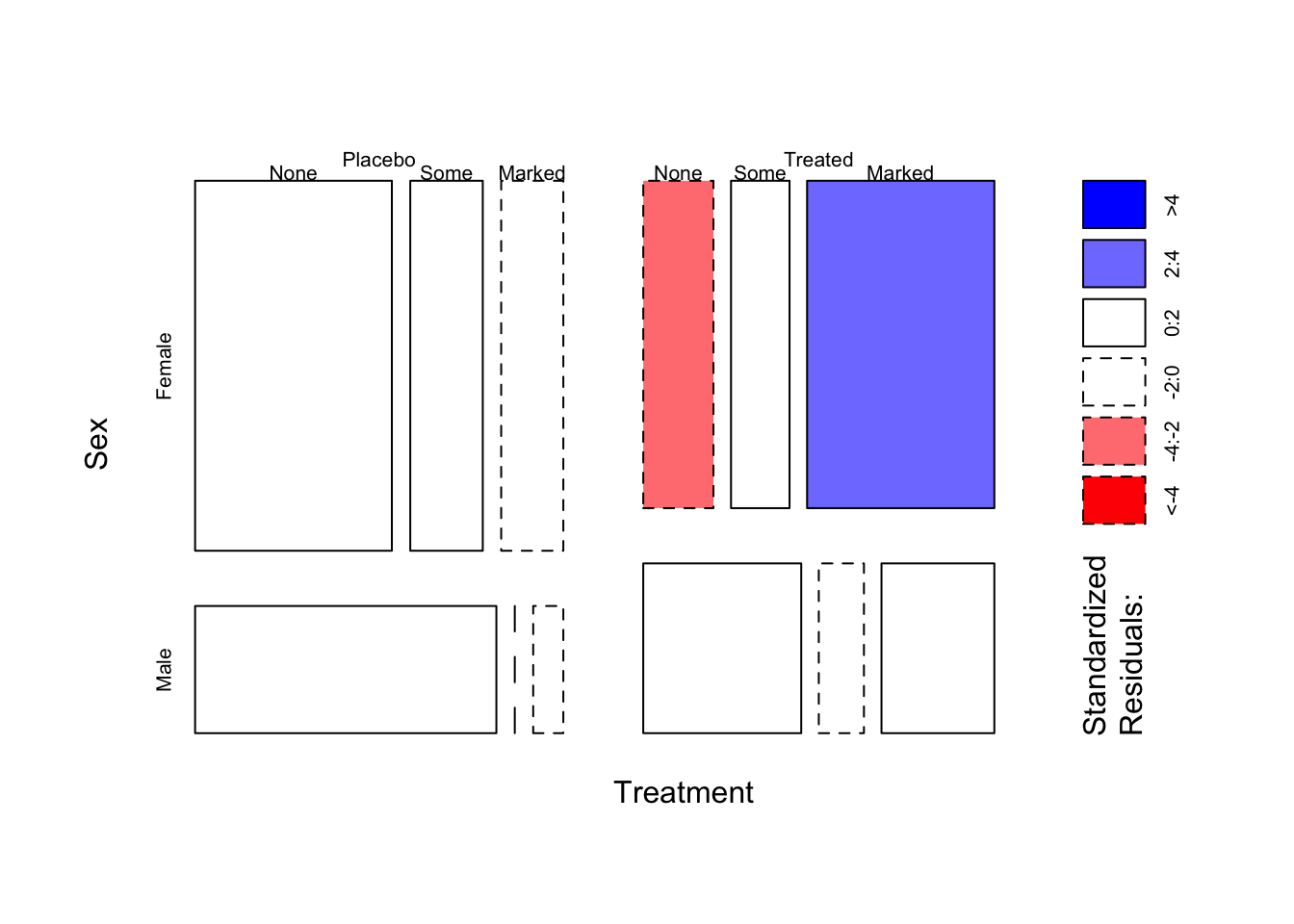

Tiles are shaded blue when more cases are observed than expected given independence, and shaded red when there are fewer cases than expected under independence. The strength of colour indicates how “surprising” those values are. The plot here is showing that most of the variation is not significant (coloured white), but in the Female and Treated group there is a surprisingly high number of patients who display a Marked improvement (blue-ish) - and consequently, fewer than expected (red-ish) whose improvement was None.

  • Use the mosaicplot function with shade and the direction arguments to create a “doubledecker” version of the mosaic plot above. 
mosaicplot(~Treatment+Sex+Improved, data=arthritis,shade=TRUE,main='',dir = c("v", "v", "h"))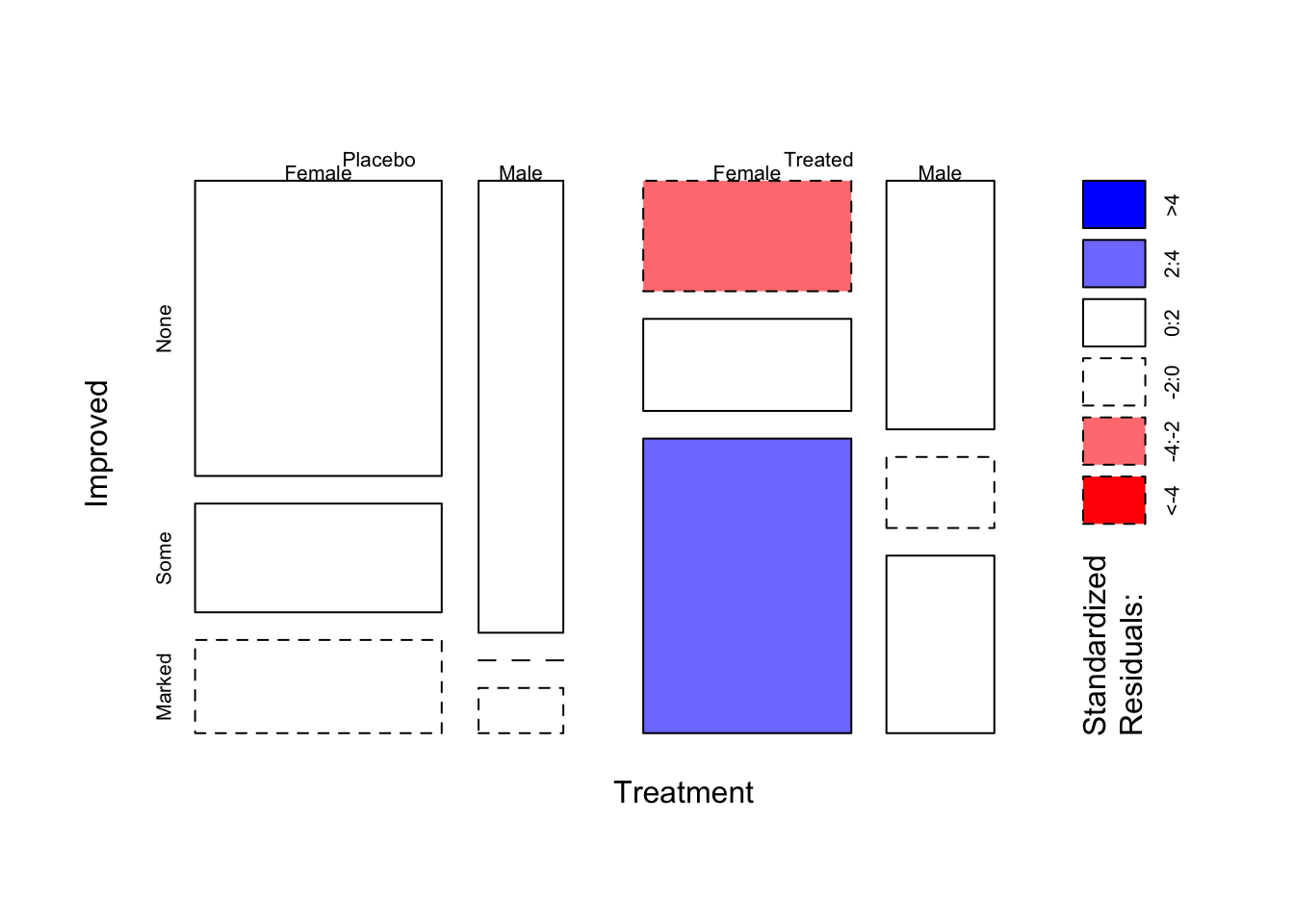

1.4 Data set 3: Alligators

Download data: alligator

The alligator data, from Agresti (2002), comes from a study of the primary food choices of alligators in four Florida lakes. The goal is to try and learn something about the food choice of the different alligators. The variables are:

  • lake - one of four lakes: George, Hancock, Oklawaha, and Trafford
  • sex - male or female
  • size - small or large
  • food - the food preferences of the alligators in five categories: fish, invertebrates, reptile, bird and other.

As usual, we begin with a quick look at the data to see what we’re dealing with:

head(alligator)
lake sex size food count
Hancock male small fish 7
Hancock male small invert 1
Hancock male small reptile 0
Hancock male small bird 0
Hancock male small other 5
Hancock male large fish 4

Here, unlike the arthritis data, each row does not represent an individual alligator but all of the alligators found with the given combinations of categorical variables. So, for example, we have seen 7 alligators with attributes (Hancock, male, small, fish). This is a slightly different format than we saw above, so we’ll need to deal with it slightly differently.

To produce the counts needed for our plots, we need to use the cross-tabulation function xtabs that we used with our barplots. So, to generate the counts of alligators in each lake, we first compute

xtabs(count~lake, data=alligator)
## lake
##   George  Hancock Oklawaha Trafford 
##       63       55       48       53

and then pass this to our mosaic function for plotting:

mosaicplot(xtabs(count~lake, data=alligator),col=2:5)

Alternatively, with a single variable we could just draw a barplot, which is probably a little easier to read!

barplot(xtabs(count~lake, data=alligator),col=2:5)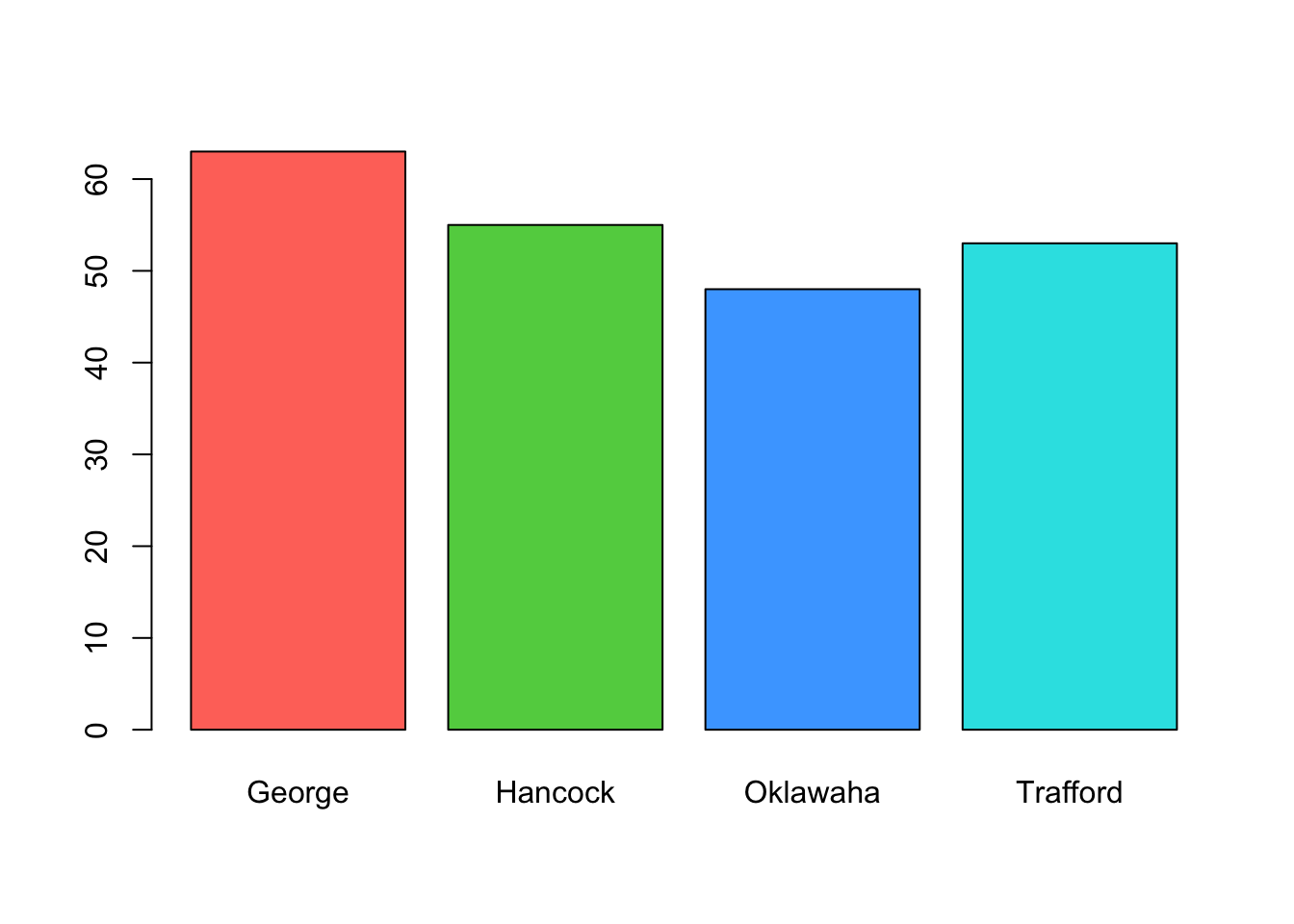

Note that the mosaicplot is showing the proportions in the different lakes by the width of the bars, whereas the barplot uses the height. We see there are slight differences between the numbers of alligators observed in the different lakes, but they don’t appear to be substantial.

Note that the only difference with working with these data (which include the counts as a variable) and the previous data set (which did not include the counts) is that we must do the aggregating of the data in the xtabs function first, instead of directly in mosaicplot. The syntax and formula for splitting the data is the same.

  • Now investigate the distributions of the other categorical variables individually: sex, size, and food. You can use whatever plot you prefer. Try and answer the following questions:
    • Are the sexes of alligators evenly distributed?
    • What about the different sizes?
    • Which food type is most popular? 
mosaicplot(xtabs(count~sex, data=alligator))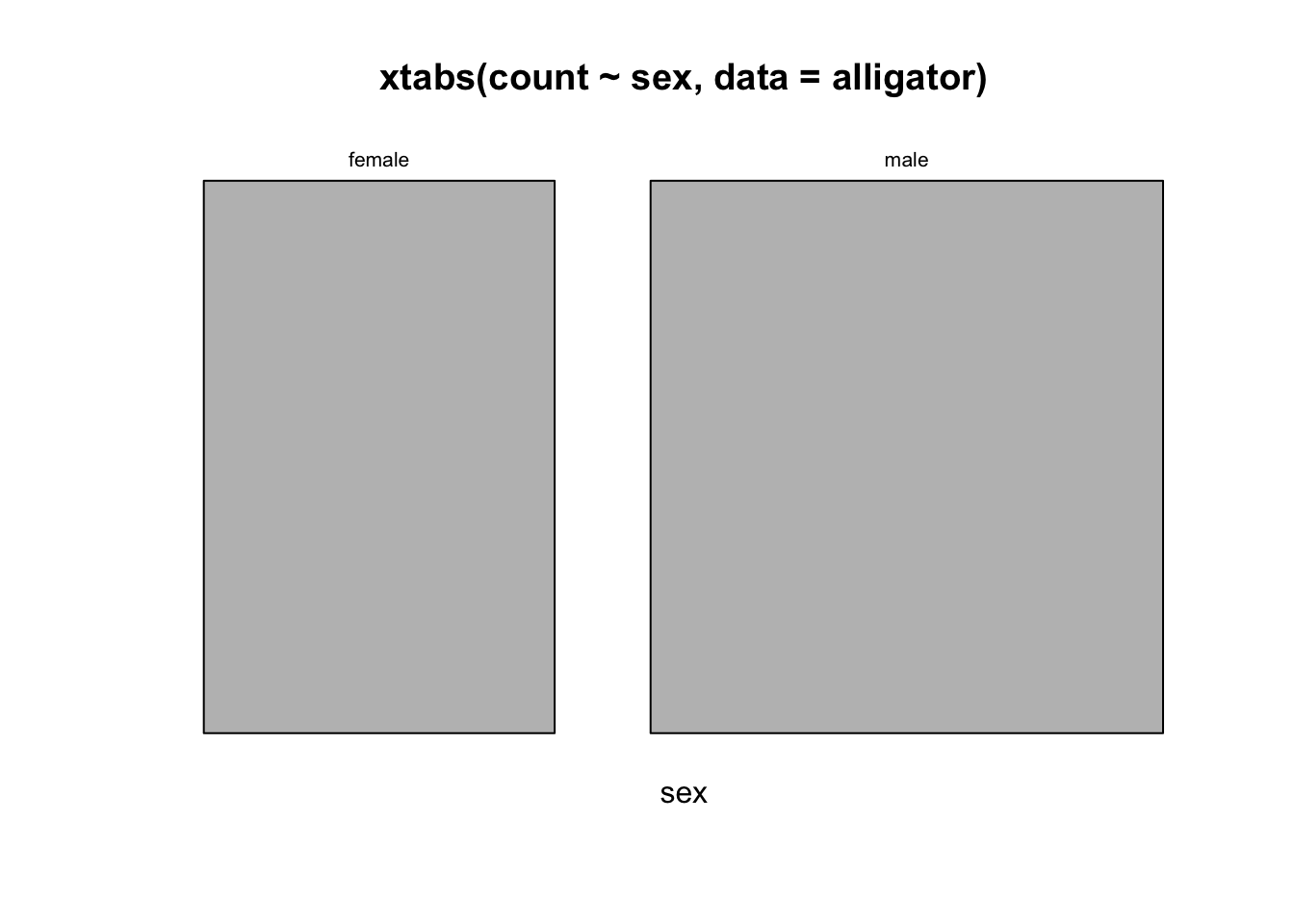

## more m than f
mosaicplot(xtabs(count~size, data=alligator))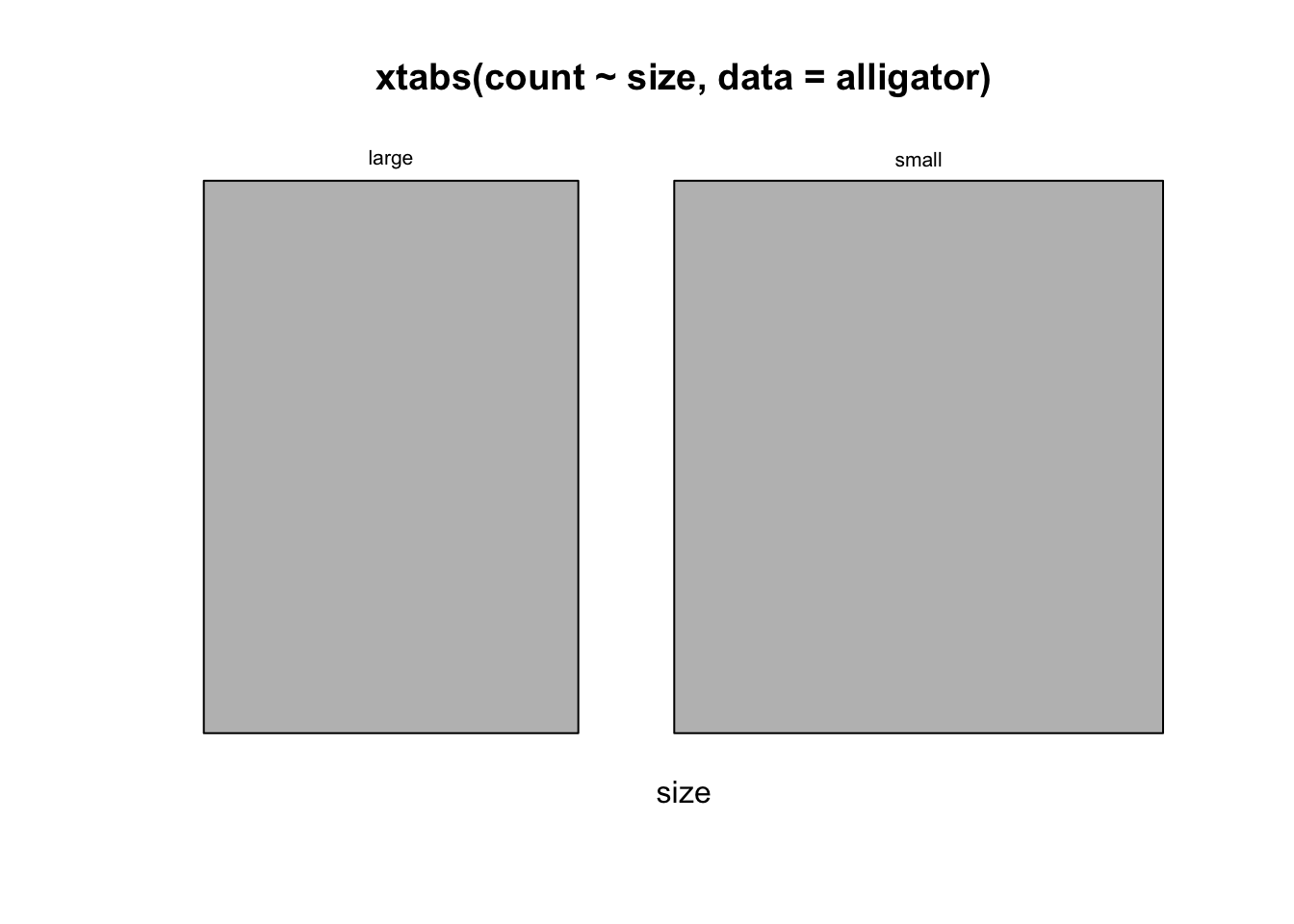

## slightly more small than large
mosaicplot(xtabs(count~food, data=alligator))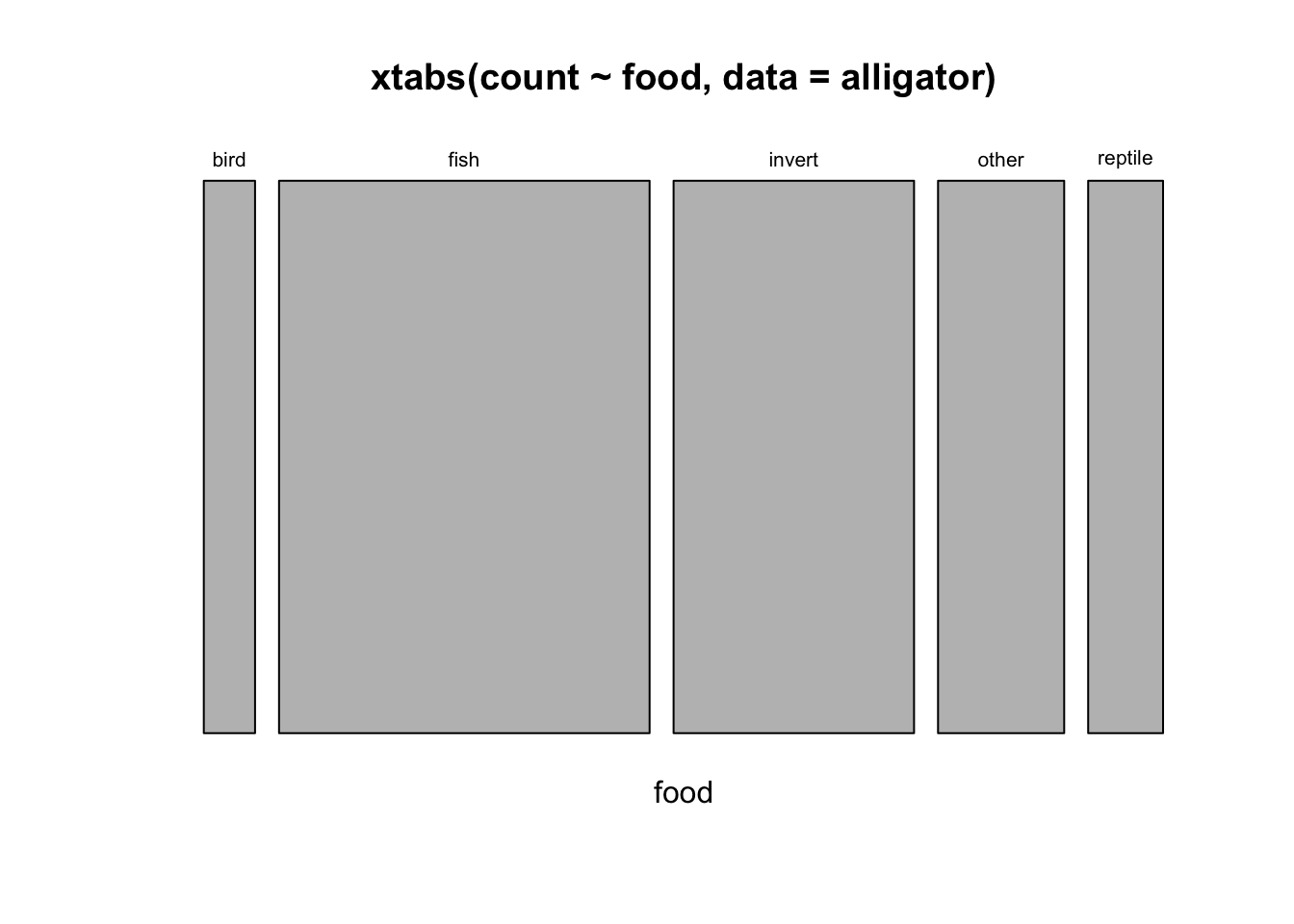

## most eat fish, then invertebrates

1.5 More than two variables

The strength of mosaic plots is when considering the combination of multiple categorical variables at once. To keep things manageable, let’s looks at some potentially interesting pairs of variables first:
  • Use mosaicplot to visualise the size and sex variables together. Remember, if there is no association here then we would expect a regular grid. What associations do you find?
  • What about size and food?
  • Draw the doubledecker plots of the same variables - how do they compare to the mosaic plot? 
mosaicplot(xtabs(count~size+sex, data=alligator))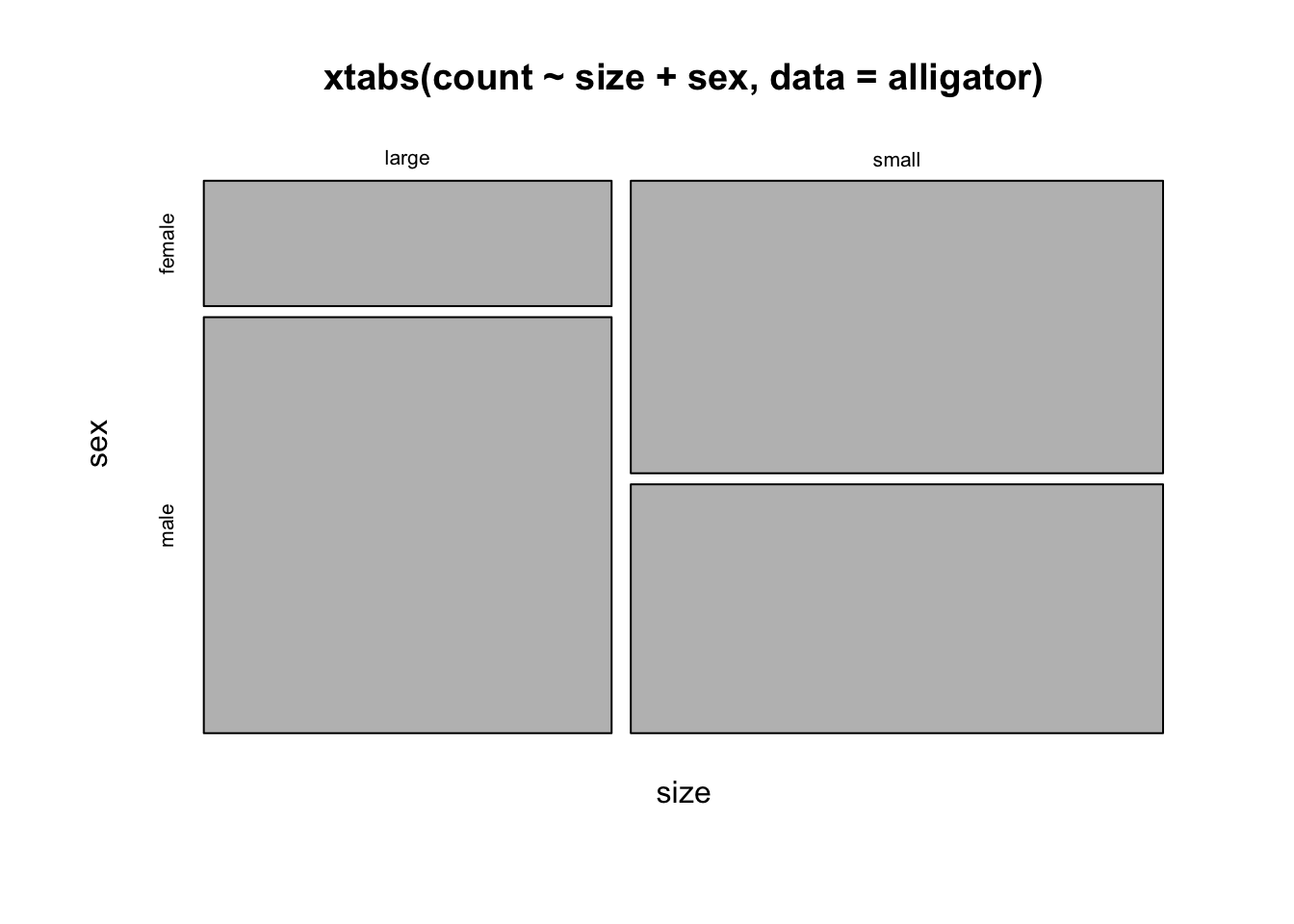

doubledecker(xtabs(count~size+sex, data=alligator))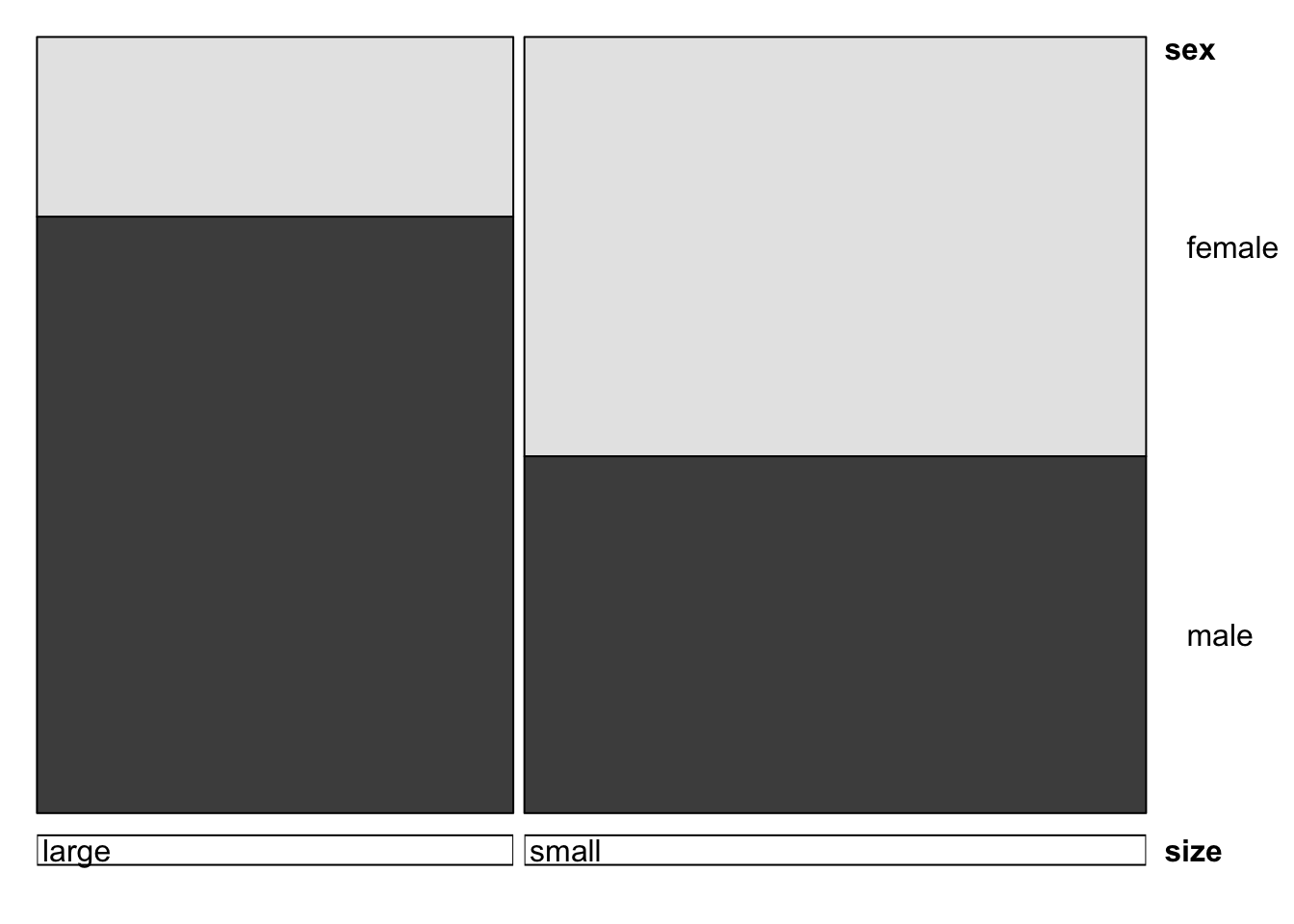

## more males are larger, females are smaller
mosaicplot(xtabs(count~size+food, data=alligator))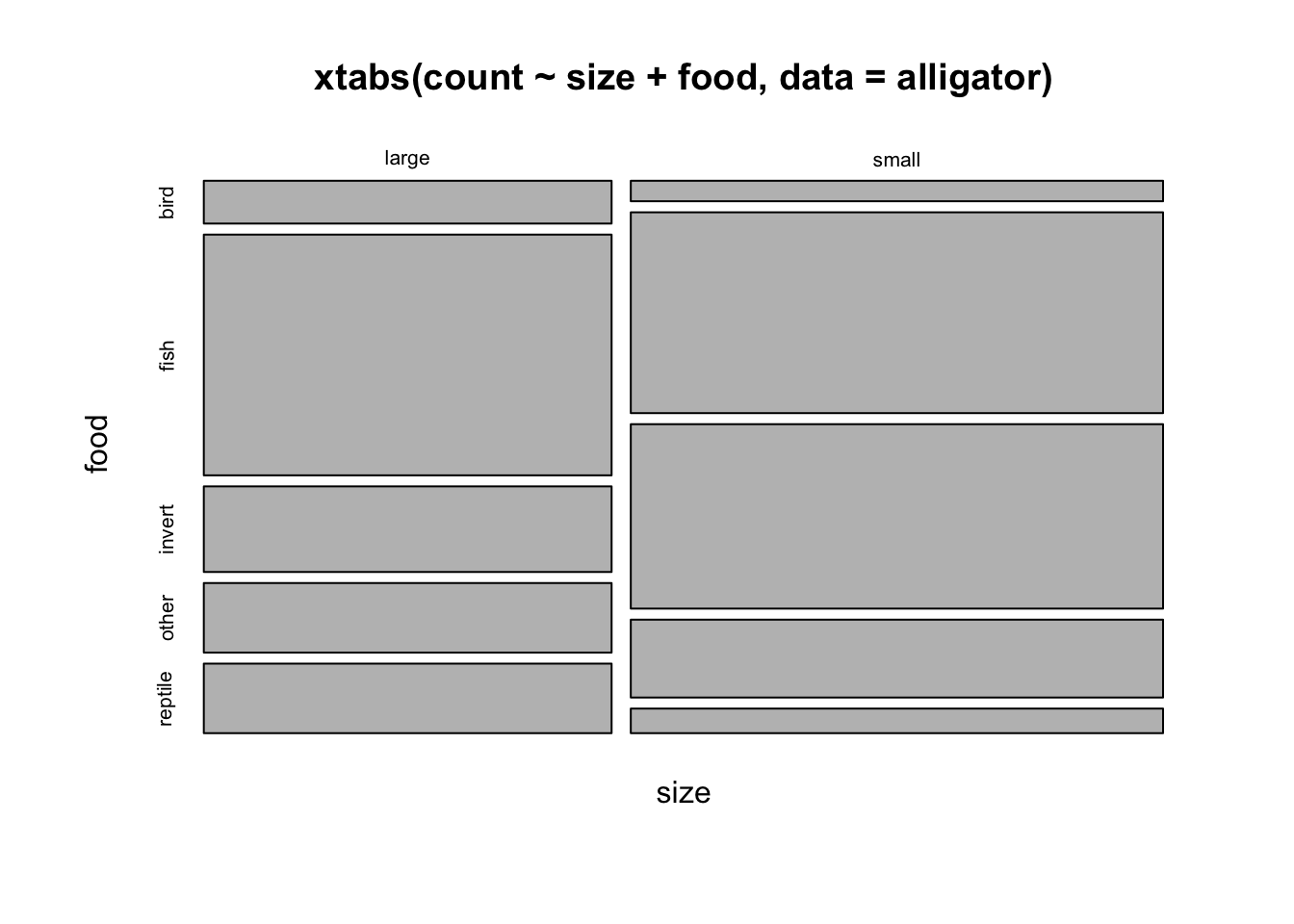

doubledecker(xtabs(count~size+food, data=alligator))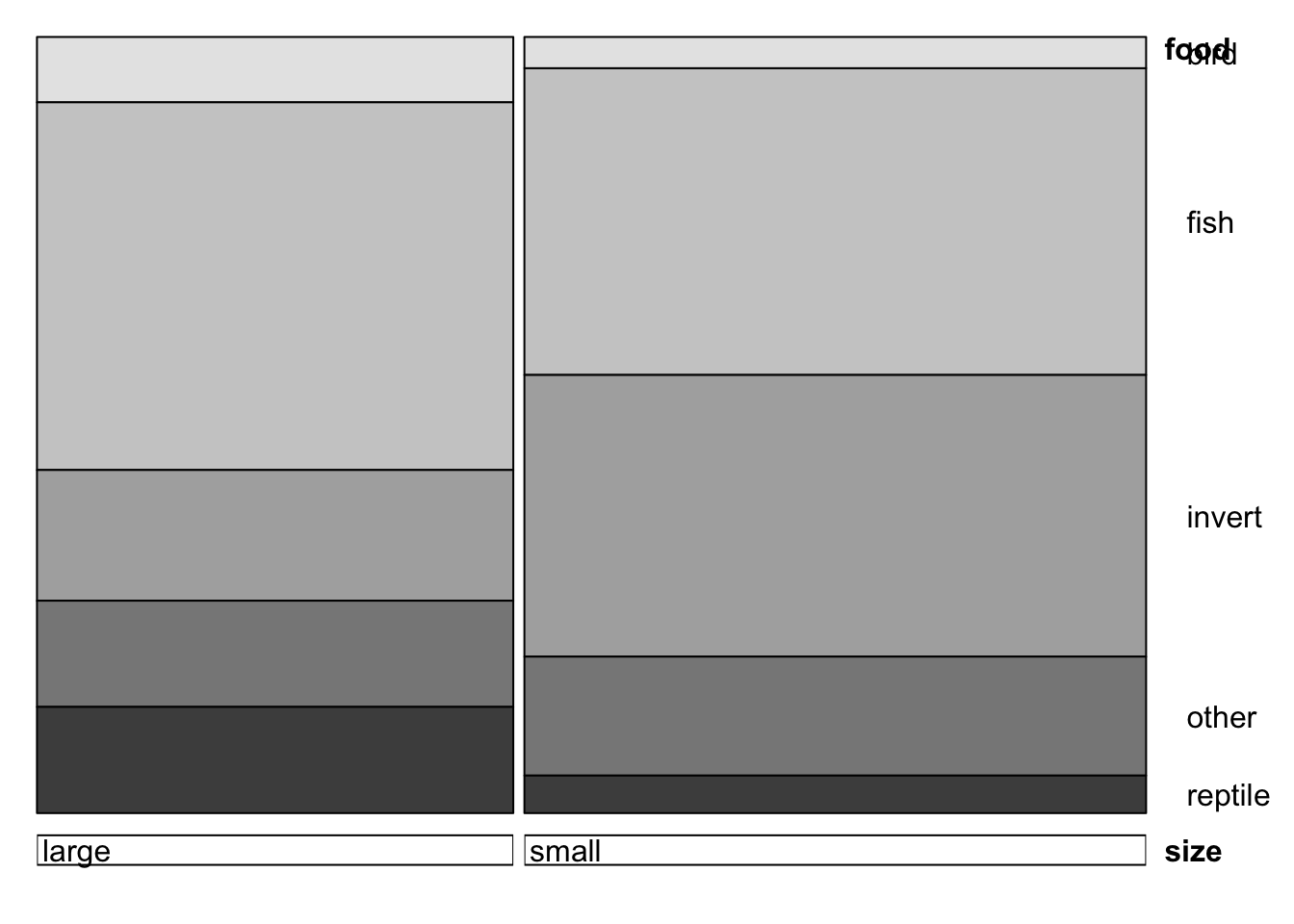

## big alligators eat more fish+reptile, and less invertebrates

We can even make a matrix of all the two-way mosaic plots in the style of a scatterplot matrix by the following command:

pairs(xtabs(count~.,data=alligator))

Using a . on the right side of the formula is a shorthand for “include everything”.

  • Can you locate the plots of size and sex, and size and food within the matrix?
  • Do you see any other potential associations (or lack of associations) here? Remember, “no association” will mean the mosaic is divided into an approximately regular grid. 
## size:sex plot is in position (1,3), size:food is in (3,4)
## seem to be a fair few associations here, except for food:sex
## take a closer look:
mosaicplot(xtabs(count~sex+food, data=alligator))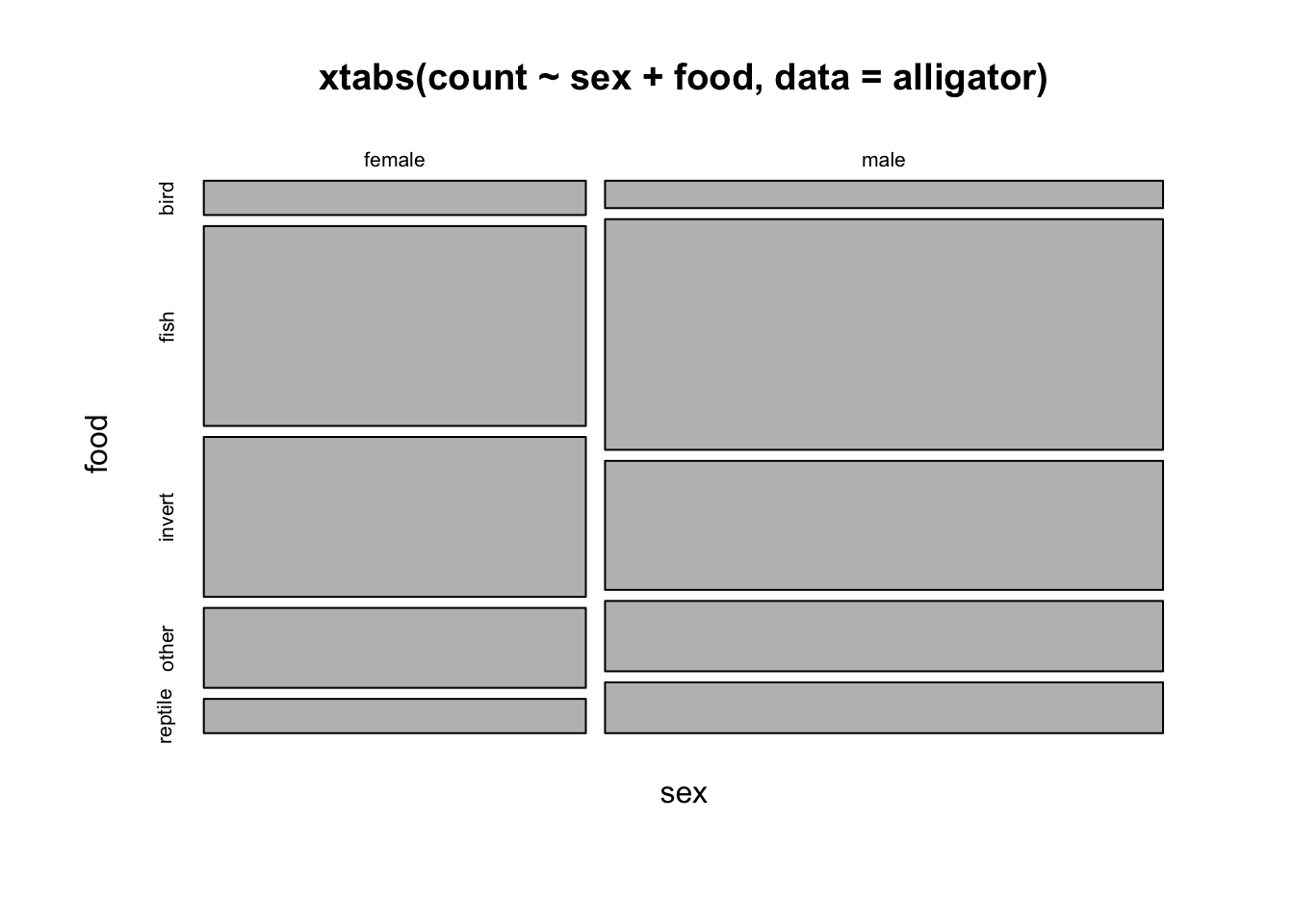

## looks pretty regular, no obvious surprisingly large/small blocks.
## Let's try shading the big plot for more emphasis
pairs(xtabs(count~.,data=alligator), shade=TRUE)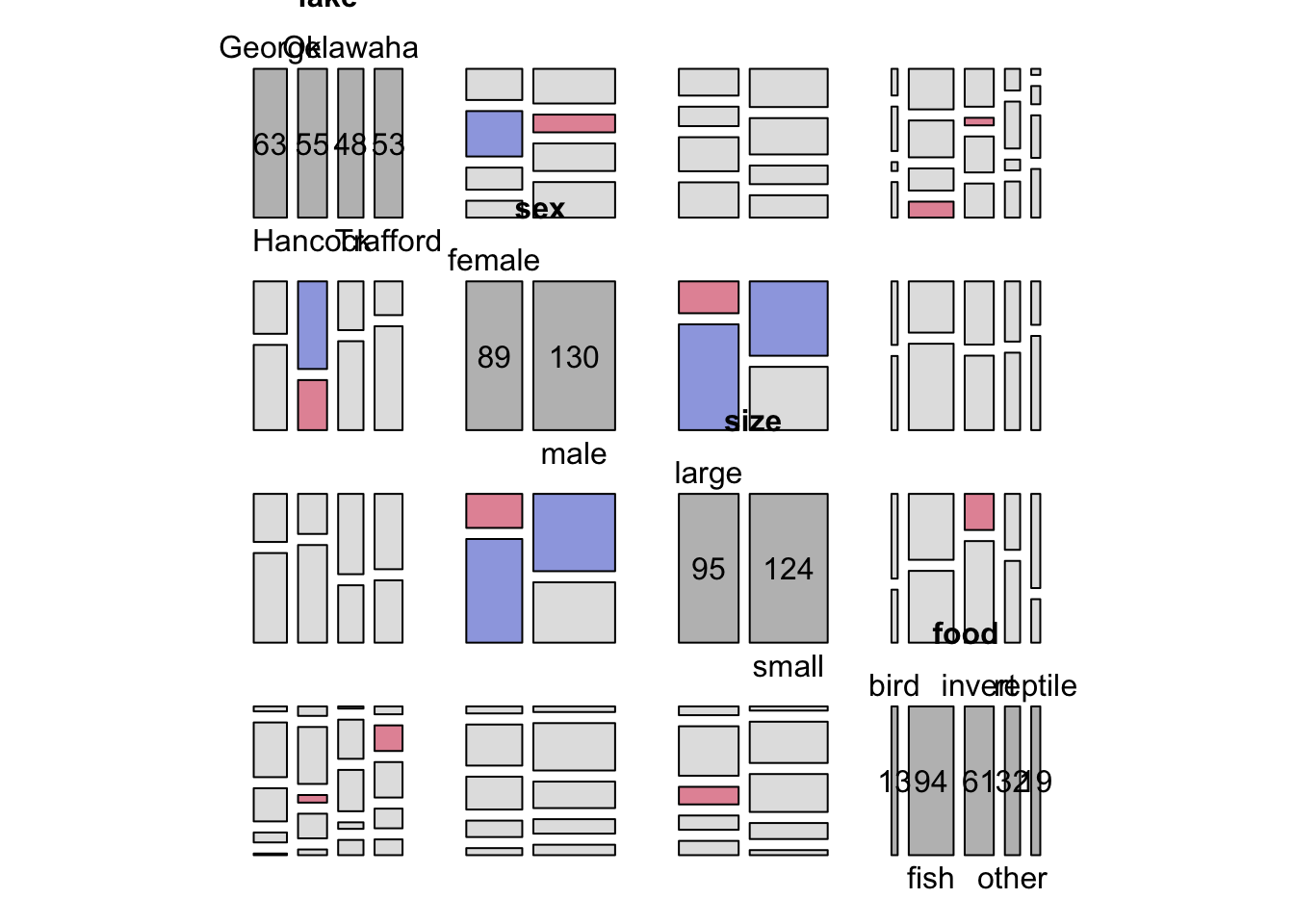

Combining more that two variables in a mosaic can get a bit crazy. Let’s look at size, sex and food all together.
  • A doubleddecker plot is often more readable at first. Make a doubledecker plot of food, size and sex - order the variables so that each bar is split into sections according to the food.
  • Now try the mosaic plot and use the shade=TRUE option. Try and achieve the same ordering so that food is the final split. What combinations have been highlighted, and how would you interpret them?
  • Do you see any other potentially interesting features here? 
doubledecker(xtabs(count~size+sex+food, data=alligator))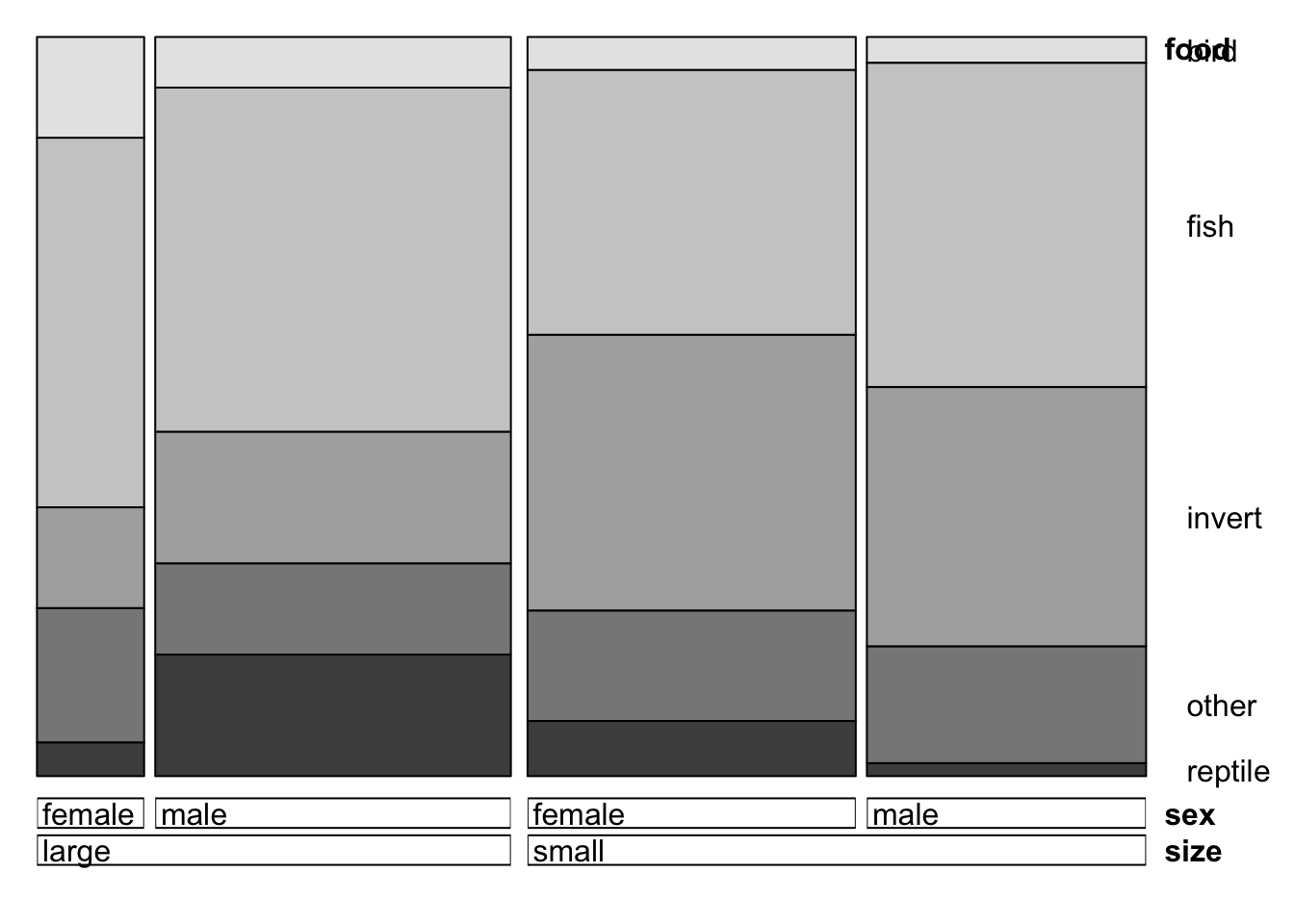

mosaicplot(xtabs(count~size+sex+food, data=alligator),shade=TRUE)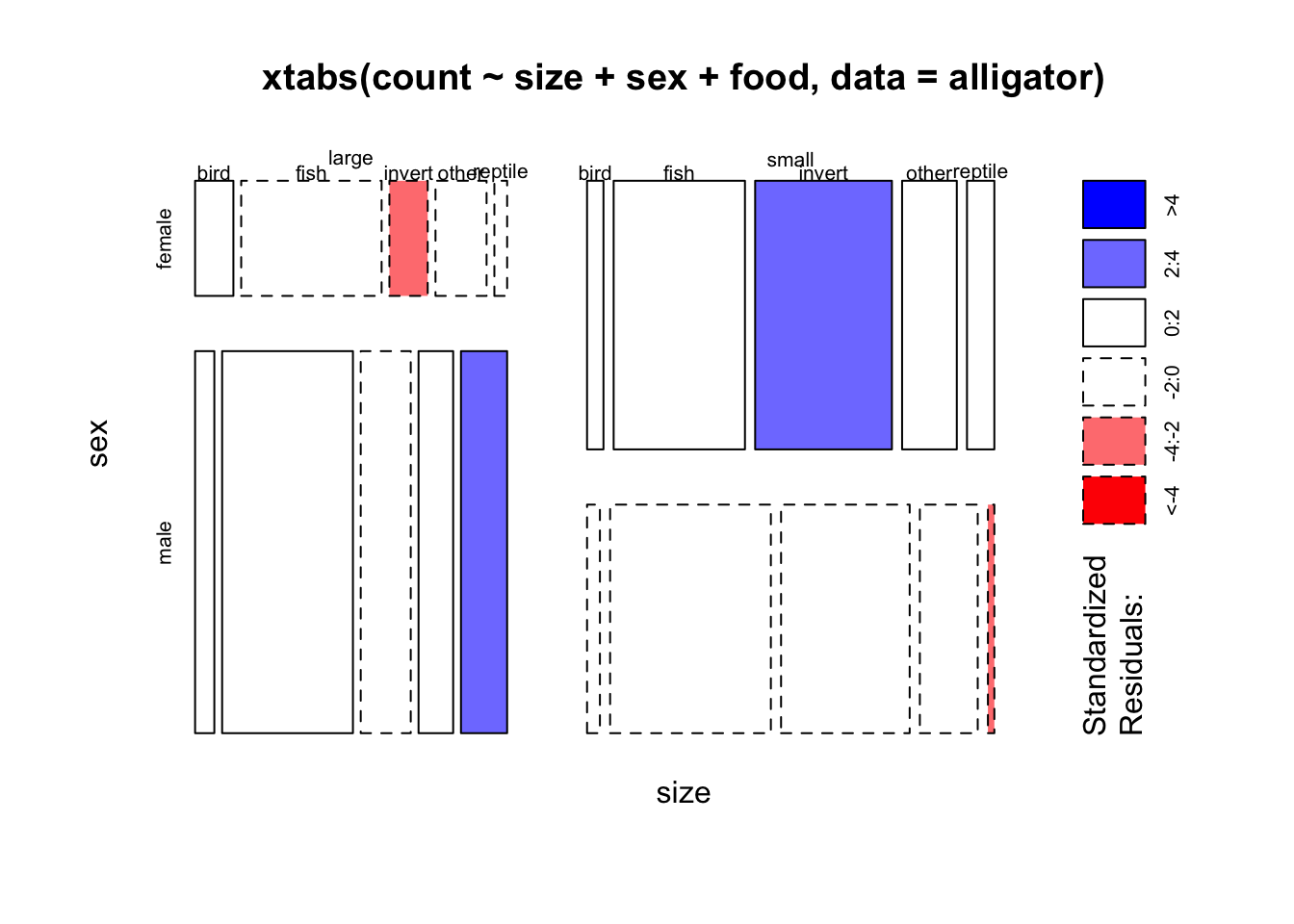

## large males eat more reptiles, small males eat surprisingly few 
## (are they eating each other...?)
## small females eat more invertebrates, large females eat few
## the four-way table goes a bit mad...
mosaicplot(xtabs(count~size+sex+food+lake, data=alligator),shade=TRUE)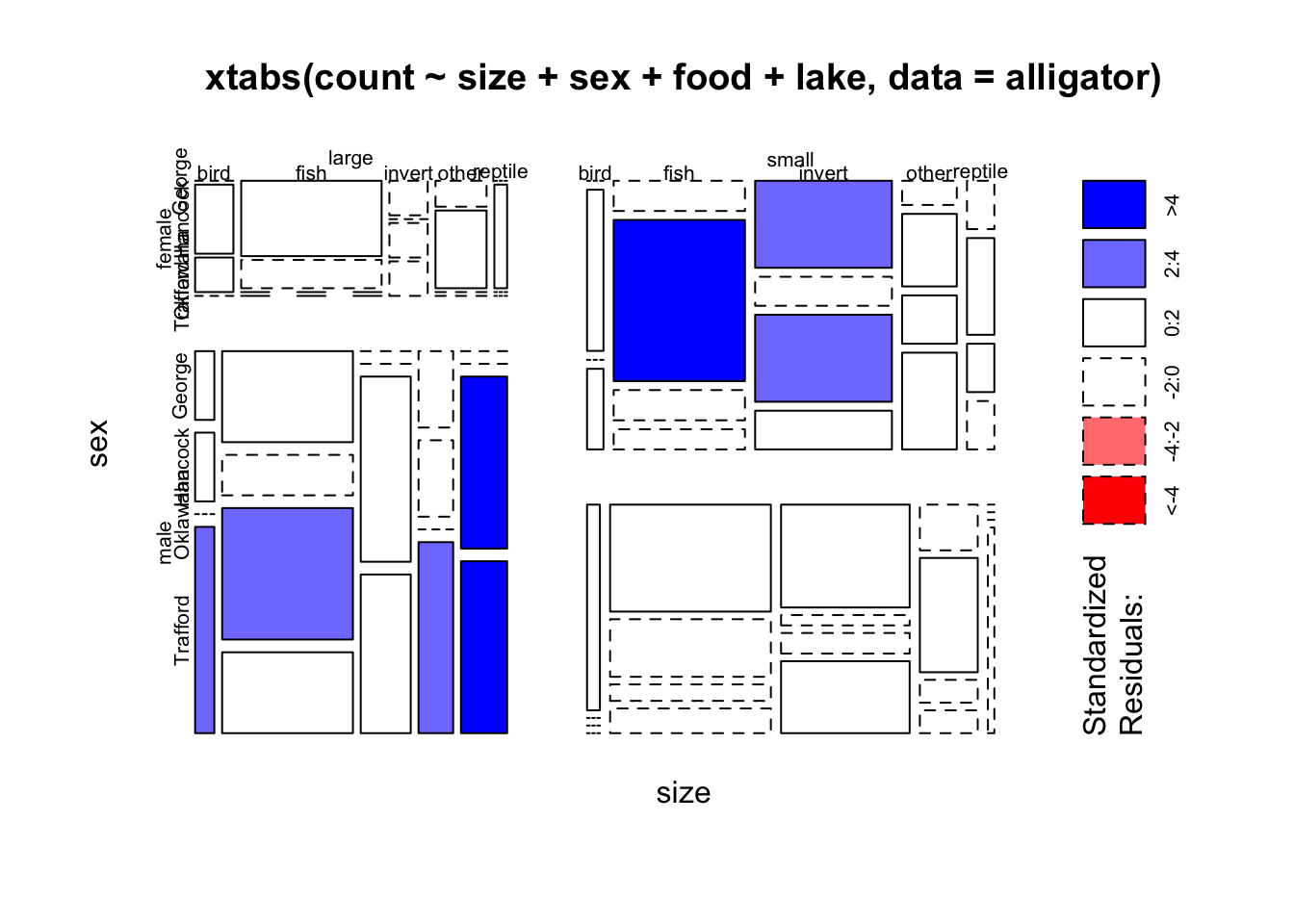

## but does reveal some features that may be worth digging into, though its
## become very hard to digest

2 Variations on Standard Plots

2.1 Grouped and stacked barplots

Barplots can be used effectively to display combinations of categorical variables. However, they require a little more setup to provide the data in the correct format.

First, a grouped barplot displays a numeric value (e.g. counts) split in groups and subgroups. A few explanation about the code below: * the input dataset must be a numeric matrix. Each group is a column. Each subgroup is a row. So we can only deal with two variables at once. * the barplot function will recognize this format, and automatically perform the grouping for you. * the beside option allows to toggle between the grouped and the stacked barchart

## make a table of counts by Treatment and Improved from the arthritis data
tab <- xtabs(~Improved+Treatment,data=arthritis)
tab
##         Treatment
## Improved Placebo Treated
##   None        29      13
##   Some         7       7
##   Marked       7      21
# Grouped barplot
barplot(tab, beside=TRUE, legend=rownames(tab), col=2:4)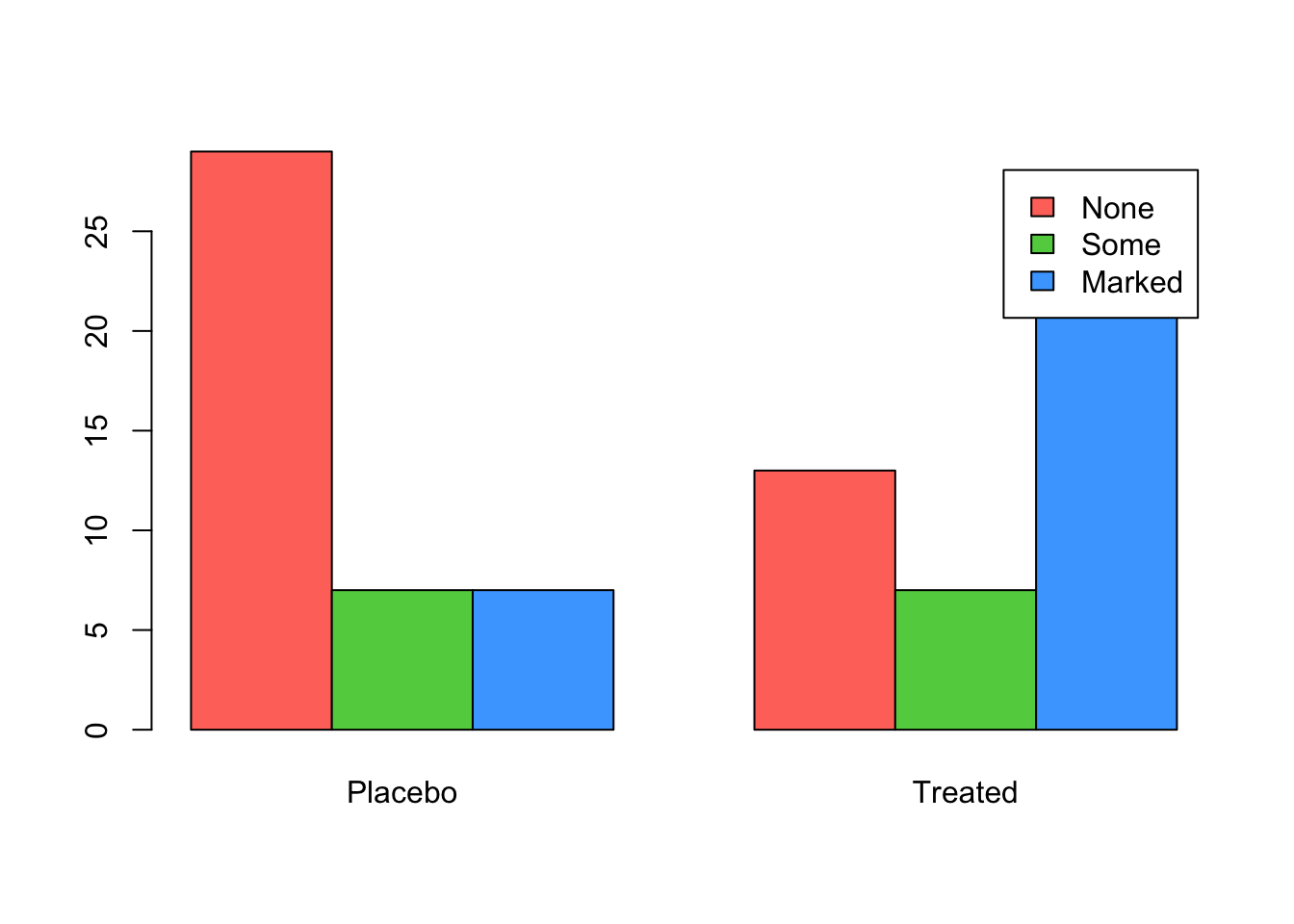

And to stack the bars, set beside=FALSE

barplot(tab, beside=FALSE, legend=rownames(tab), col=2:4)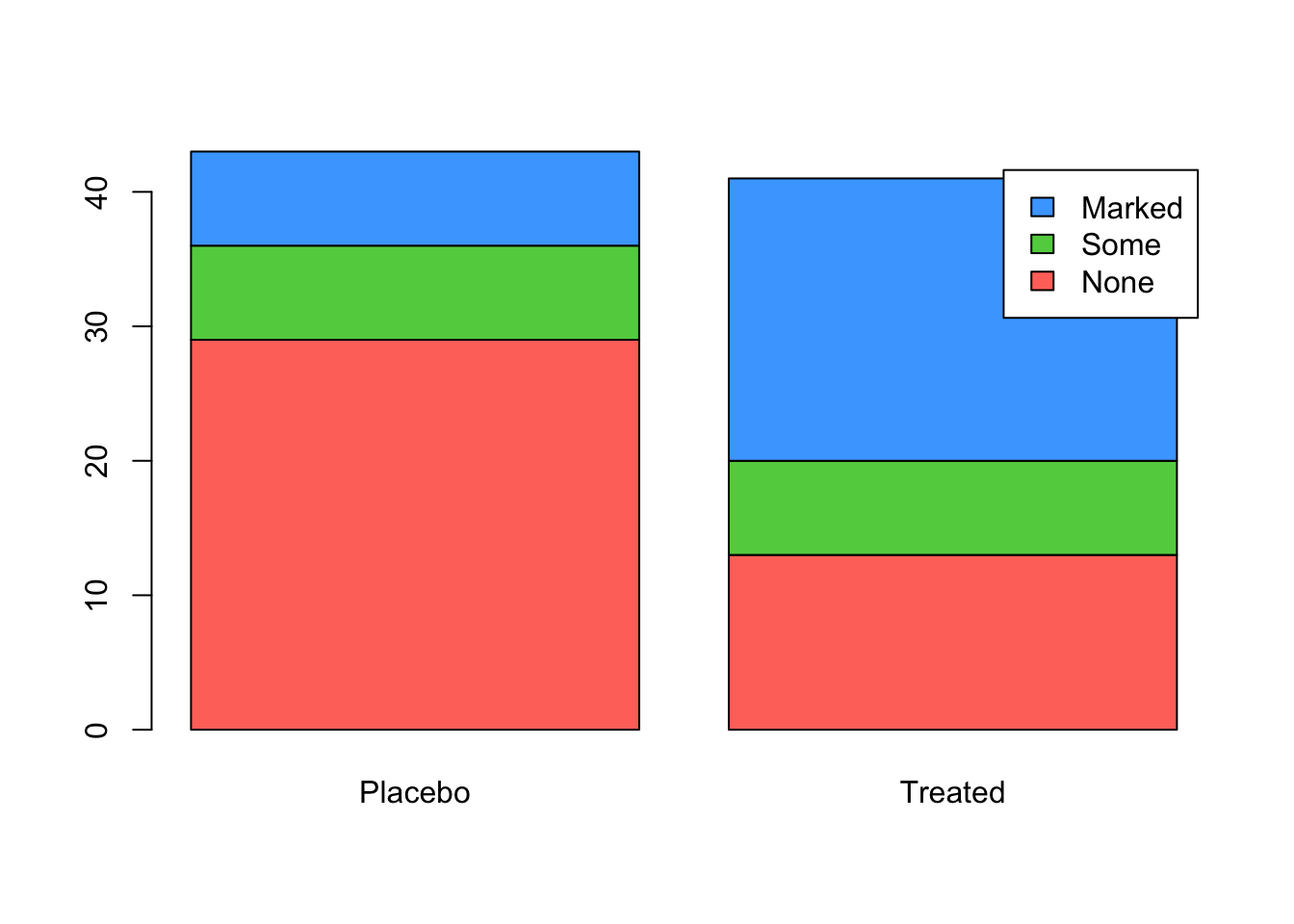

Stacked bars are often used to display the proportions of the respective columns attributable to each sub-group. Thankfully, we can easily convert tables of counts to proportions with the prop.table function. If we want the proportions computed within a column, set the margin=2 argument:

barplot(prop.table(tab, margin=2), beside=FALSE, legend=rownames(tab), col=2:4)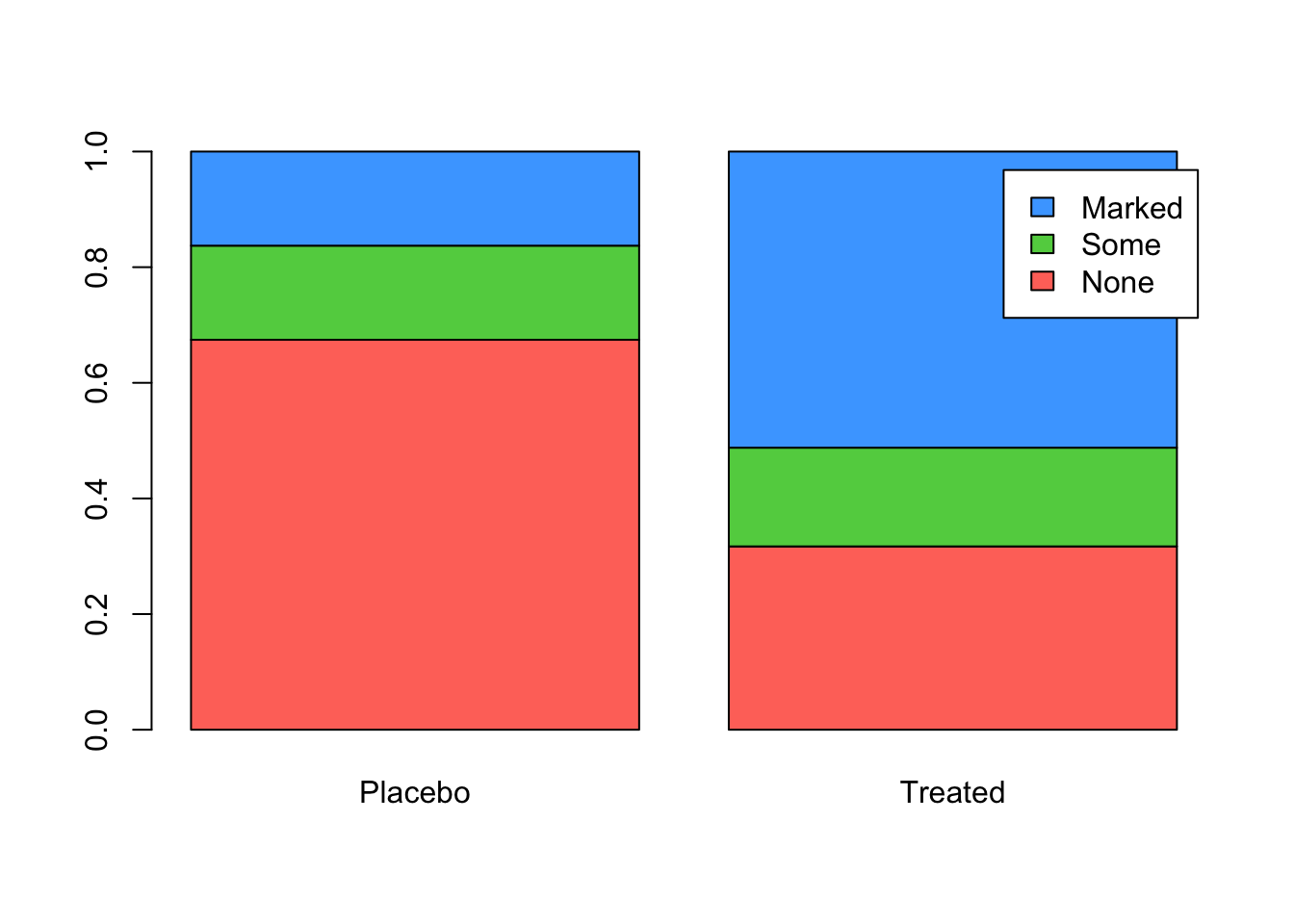

3 More Practice

3.1 Data set: Airline arrivals

Download data: airlineArrival

The airlineArrival data contains 11000 observations of 3 categorical variables: * Airport - a factor with levels LosAngeles, Phoenix, SanDiego, SanFrancisco, Seattle * Result - a factor with levels Delayed,OnTime * Airline - a factor with levels Alaska, AmericaWest

  • Is there much difference in the amount of delayed flights between the two airlines?
  • What about the delays from different airports? Which look best for flights being on time? Which look worst?
  • Now look at whether both Airport and Airline are associated with delays. What do you find? Try turning on shade=TRUE.
  • In which plot are the associations most pronounced?

3.2 Data set: Winter Olympic Medals

Download data: medals

The medals data contains the number of medals won at the 2016 Summer Olympics. The variables are * NOC - the country * country - a factor indicating the country code * medal - a factor with levels Bronze, Silver, and Gold * count - the number of medals of that type won by that country

  • Try drawing a mosaic or doubledecker plot between country and medal.
  • With the huge number of possible countries, this isn’t going to work.
  • Let’s try some stacked barplots instead. Read the section on stacked barplots above.
  • Make a stacked barplot showing the different countries on the x axis, with each bar split by the type of medal.
  • There are probably too many countries here. Use the Total variable to make a new data set containing only the records for countries which won more that 10 medals. Redraw your plot.
  • Try drawing the barplot horizontally (horiz=TRUE) and rotate the labels (las=2).
  • Set the colours of the bars to use “#D4AF37” for Gold, “#C0C0C0” for Silver, and “#CD7F32” for Bronze.
  • To finish off the plot, lets rearrange the bars into order
    • Find the medal totals for each of the remaining countries, save this table to a variable.
    • Apply the colSums function to the table to get the medal totals per country, and save this to another variable.
    • Use the order function to order the medal totals in decreasing order (decreasing=TRUE), and save this.
    • Now use the results of the order function at the previous step to rearrange the columns of the medals table, and save it.
    • Now draw the final barplot of our rearranged table!