Chapter 5 Ensemble methods
It is often said that two heads are better than one. This principle also applies to machine learning, where combining multiple models can lead to better performance than any individual model. Ensemble methods leverage the diversity of multiple models to create a more robust and accurate prediction. In this chapter, we will explore some popular ensemble methods including stacking, bagging, random forests, and boosting. Again, we will be using the same running examples as from the previous chapters to illustrate these concepts.
Let’s first consider some of the mathematics behind why ensemble methods work. The key idea is that combining multiple models can help reduce bias and variance, leading to better generalisation performance. This is known as the bias-variance trade-off, which we met earlier. Mathematically, the expected prediction error of a model can be decomposed into three components:
\[\begin{align*} \text{Expected Prediction Error} = \text{Bias}^2 &+~ \text{Var} \\ &~~~~~~+~ \text{Irreducible Error}. \end{align*}\]
When we utilise two models \(f_1\) and \(f_2\) to make predictions, the expected prediction error of the ensemble can be expressed as:
\[\begin{align*} \text{Expected Prediction Error} &= \text{Bias}^2 + \text{Var} + \text{Irreducible Error}\\ &~~~~~~~~+ \text{constant}*\text{Covariance}(f_1, f_2). \end{align*}\]
The covariance term captures the relationship between the predictions of the two models. If the models are highly correlated, the covariance term will be positive, and the ensemble may not benefit much from combining them. However, if the models are uncorrelated or negatively correlated, the covariance term will act to reduce the variance in the prediction, and the ensemble can achieve a lower expected prediction error than any individual model.
Let’s concentrate on the more statistical idea of model averaging. If our ensemble prediction is of the form:
\[ f_{\text{Ensemble}}(X) = \alpha f_1(X) + (1 - \alpha) f_2(X), \] where \(\alpha \in [0,1]\) is a weight that determines the contribution of each model. The variance of the ensemble prediction with respect to unknown explanatory variables can be expressed as: \[ \begin{aligned} \text{Var}(f_{\text{Ensemble}}(X)) &= \text{Var}(\alpha f_1(X) + (1 - \alpha) f_2(X)) \\ &= \alpha^2 \text{Var}(f_1(X)) + (1 - \alpha)^2 \text{Var}(f_2(X)) \\&~~~~~ + 2\alpha(1 - \alpha)\text{Cov}(f_1(X), f_2(X)). \end{aligned} \] Here, if \(f_1(x)=f_2(x)\), we return the variance in predictions from that single model. If we have two models that are uncorrelated, the covariance term will be zero, and the variance of the ensemble prediction will be lower than the variance of the individual models. This is the key idea behind ensemble methods: by combining multiple models that are diverse and uncorrelated, we can reduce the variance of the ensemble prediction and improve the overall (average) performance of the model. However, we limit the ability of the ensemble to capture more extreme and complex patterns in the data.
5.1 Weak and strong learners
In the context of ensemble learning, a weak learner is a model that performs slightly better than random guessing on a given task. Weak learners are typically simple models that have limited predictive power but can still provide some useful information. Examples of weak learners include decision stumps (decision trees with a single split), linear models, and shallow neural networks.
In contrast, a strong learner is a model that performs well above random guessing on a given task. Strong learners have high predictive power and can accurately capture complex patterns in the data. Examples of strong learners include deep neural networks, gradient-boosted trees, and support vector machines (which you will learn about next term).
5.2 Stacking
Stacking, also known as stacked generalisation, is a technique in machine learning that combines the predictions from multiple models to create a new, improved model. It is a type of ensemble method that leverages the strengths of various models to achieve better performance than any individual model could on its own.
Here’s a breakdown of how stacking works:
- Train multiple base models: You start by training several different machine learning models on the same dataset. These models can be of different types.
- Make predictions with base models: Use each base model to make predictions on a separate hold-out validation set (data not used for training). This gives you multiple predictions for each data point in the validation set.
- Train a meta-model: Now, you train a new model, called a meta-model or stacking model, using the predictions from the base models as features. The target variable for the meta-model is the actual value in the validation set.
- Final predictions: The meta-model learns how to best combine the predictions from the base models to create a final prediction. This final prediction is often expected to be more accurate than the predictions from any of the individual base models.
Stacking essentially allows you to harness the strengths of different models and potentially address their weaknesses. By combining their insights, the final model can achieve a more robust and generalisable performance.
Figure 5.1 illustrates the concept of stacking from the point of view of making predictions.
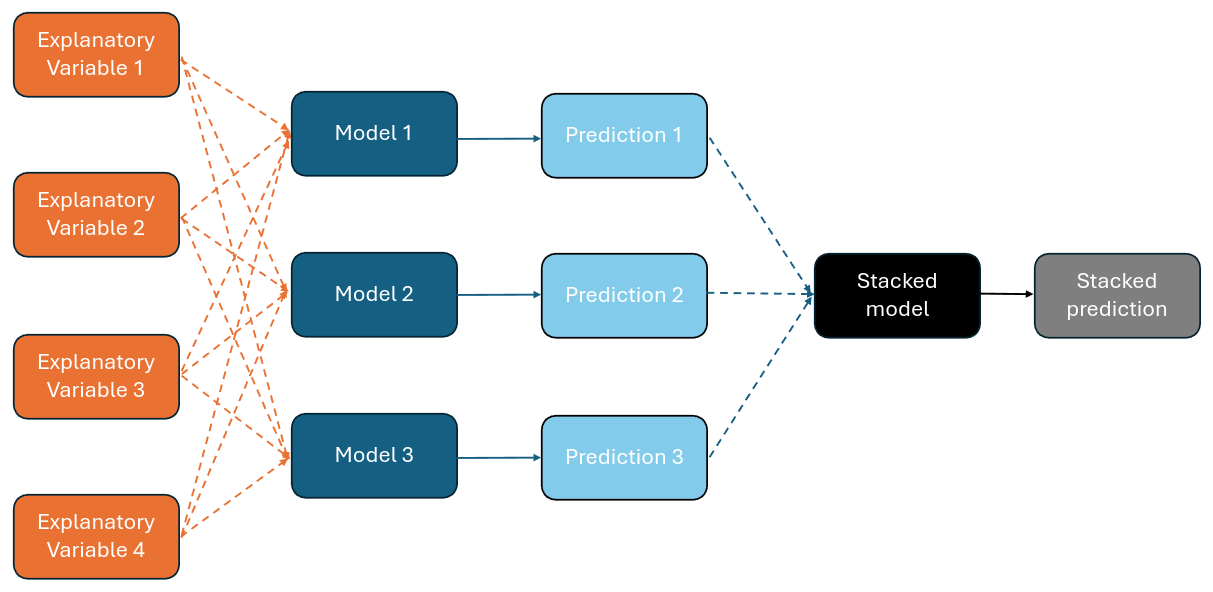
Figure 5.1: Combining models to make stacked predictions
5.2.1 Stacking of classifiers
In this example, we will demonstrate how to implement stacking in R. We will train multiple base models on the iris dataset and then use a meta-model to combine their predictions.
# Load the required libraries
library(caret)
library(e1071)
# Load the iris dataset
data(iris)
# Create a training and validation set using the sample function
set.seed(123)
train_index <- sample(1:nrow(iris), 0.8 * nrow(iris))
train <- iris[train_index, ]
test <- iris[-train_index, ]
# Define the base models
# (multinomial regression, kNN and the naive Bayes classifier)
model1 <- train(Species ~ ., data = train,
method = "multinom", trace = FALSE)
model2 <- train(Species ~ ., data = train,
method = "knn")
model3 <- train(Species ~ ., data = train,
method = "naive_bayes")
# Make predictions on the validation set
pred1 <- predict(model1, newdata = test)
pred2 <- predict(model2, newdata = test)
pred3 <- predict(model3, newdata = test)
# Combine the predictions into a data frame alongside the actual values
stacked_data <- data.frame(pred1, pred2, pred3,
Species = test$Species)
# Train a meta-model (decision trees) on the stacked data
meta_model <- train(Species ~ ., data = stacked_data,
method = "rpart")
# Make predictions with the meta-model
final_pred <- predict(meta_model,
newdata = stacked_data)
# Evaluate the performance of the meta-model
confusionMatrix(test$Species,final_pred)$table## Reference
## Prediction setosa versicolor virginica
## setosa 10 0 0
## versicolor 1 14 0
## virginica 5 0 0As a contrast, we also show the confusion matrices from the three separate models:
## Reference
## Prediction setosa versicolor virginica
## setosa 10 0 0
## versicolor 0 14 1
## virginica 0 0 5## Reference
## Prediction setosa versicolor virginica
## setosa 10 0 0
## versicolor 0 14 1
## virginica 0 0 5## Reference
## Prediction setosa versicolor virginica
## setosa 10 0 0
## versicolor 0 14 1
## virginica 0 0 5So, the \(k\)-nearest neighbours model is the best one and as good as the stacked model in its own right. There is also an issue with overfitting here again because we are training the meta model on the same data as we are testing it on. This is a common issue with stacking and can be addressed by using cross-validation to train the meta-model or by simply splitting the data into three parts: training, validation, and testing.
Let’s rerun the analysis with a 60-20-20 split:
# Create a training, validation and test set using the sample function
set.seed(147)
train_index <- sample(1:nrow(iris), 0.6 * nrow(iris))
validation_index <- sample(setdiff(1:nrow(iris), train_index),
0.2 * nrow(iris))
test_index <- setdiff(1:nrow(iris),
c(train_index, validation_index))
train <- iris[train_index, ]
validation <- iris[validation_index, ]
test <- iris[test_index, ]
# Define the base models
# (multinomial regression, kNN and the naive Bayes classifier)
model1 <- train(Species ~ ., data = train,
method = "multinom", trace = FALSE)
model2 <- train(Species ~ ., data = train,
method = "knn")
model3 <- train(Species ~ ., data = train,
method = "naive_bayes")
# Make predictions on the validation set
pred1 <- predict(model1, newdata = validation)
pred2 <- predict(model2, newdata = validation)
pred3 <- predict(model3, newdata = validation)
# Combine the predictions into a data frame alongside the actual values
stacked_data <- data.frame(pred1, pred2, pred3, Species = validation$Species)
# Train a meta-model (decision trees) on the stacked data
meta_model <- train(Species ~ ., data = stacked_data, method = "rpart")
# Make predictions for the test set with the meta-model
final_pred <- predict(meta_model,
newdata = data.frame(pred1 = predict(model1,
newdata = test),
pred2 = predict(model2,
newdata = test),
pred3 = predict(model3,
newdata = test)))
# Evaluate the performance of the meta-model
confusionMatrix(test$Species, final_pred)$table## Reference
## Prediction setosa versicolor virginica
## setosa 9 0 0
## versicolor 11 0 1
## virginica 0 0 9Again, we can compare the performance of the stacked model with the individual models for the test data.
## Reference
## Prediction setosa versicolor virginica
## setosa 9 0 0
## versicolor 0 11 1
## virginica 0 0 9## Reference
## Prediction setosa versicolor virginica
## setosa 9 0 0
## versicolor 0 12 0
## virginica 0 0 9## Reference
## Prediction setosa versicolor virginica
## setosa 9 0 0
## versicolor 0 12 0
## virginica 0 1 8The stacked model does not look so good this time as it is still better to use the \(k\)-nearest neighbours model on its own. The plot of the fitted decision tree in the stacked model is shown below:
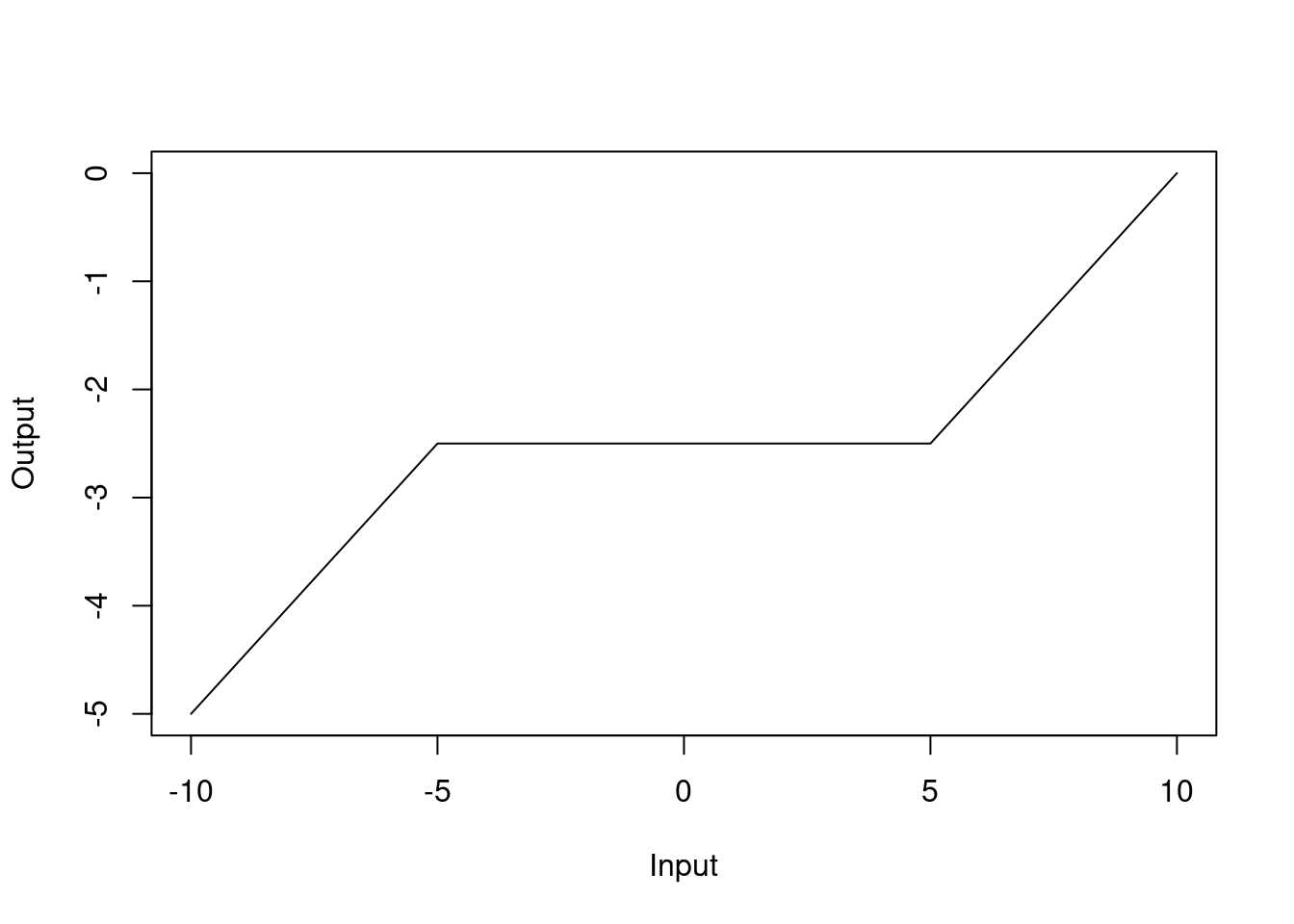
Figure 5.2: Fitted decision tree for the stacked model
Interestingly, the second model is completely ignored in the decision tree. This is a common issue with stacking, where the meta-model can sometimes ignore the predictions from certain base models if they are not contributing to the overall performance. The reason for this can be seen in the confusion matrices for the validation set:
## Reference
## Prediction setosa versicolor virginica
## setosa 8 0 0
## versicolor 0 6 2
## virginica 0 0 14## Reference
## Prediction setosa versicolor virginica
## setosa 8 0 0
## versicolor 0 6 2
## virginica 0 0 14## Reference
## Prediction setosa versicolor virginica
## setosa 8 0 0
## versicolor 0 7 1
## virginica 0 2 12The second model is performing in precisely the same way as the first model, so the meta-model has no reason to use it. The third model is at least handling the versicolor class better than the first two models, so it is used in the meta-model.
5.3 Bagging
Bagging is an ensemble method that aims to reduce the variance of a machine learning model and improve its overall stability. It achieves this by training multiple models, called base learners, on different subsets of the data and then aggregating their predictions. The name “bagging” is short for “bootstrap aggregating,” as it uses bootstrapping to create the data subsets.
5.3.1 Bootstrapping
Bootstrapping is a resampling technique used in statistics. It is often mistaken for a method that generates psuedo-data-points, but it is actually a way to create multiple datasets from the original data by sampling with replacement. This allows us to estimate the uncertainty of a statistic without the need for additional data collection. There is an assumption that the original data is representative of the population, and the bootstrapped samples are representative of the original data.
Here’s how bagging works:
Create bootstrap samples: Bagging starts by generating multiple random samples (with replacement) from the original training data. These samples, called bootstrap replicates, are of the same size as the original data but may contain duplicates of some data points and exclude others.
Train base learners in parallel: Each bootstrap replicate is used to train a separate base learner independently. These base learners can be any type of model, but decision trees are commonly used with bagging.
Aggregate predictions: After training all the base learners, their predictions are combined. For regression tasks, the predictions are typically averaged. In classification tasks, a majority vote is often used, where the class with the most votes from the base learners becomes the final prediction.
By training on various data subsets and averaging/voting their predictions, bagging reduces the influence of any single data point on the final model. This helps to address overfitting and leads to a more generalisable model that performs well on unseen data. Bagging has a random component due to the bootstrapping process, which adds diversity to the base learners and improves the overall performance of the ensemble. It may be worth considering training alternatives based on jackknife resampling or one-at-a-time cross-validation where the randomness is eliminated.
Example
Let’s consider a bagged lasso regression model using the boot package in R. We will use the Boston dataset to demonstrate bagging with a lasso regression model.
# Load the Boston dataset
data(Boston)
# Create a training and test set using the sample function
set.seed(123)
train_index <- sample(1:nrow(Boston), 0.8 * nrow(Boston))
train <- Boston[train_index, ]
test <- Boston[-train_index, ]
# Define the base model (lasso regression)
library(glmnet)## Loading required package: Matrix## Loaded glmnet 4.1-8base_model <- function(data, indices) {
fit <- glmnet(x = as.matrix(data[indices, -14]), y = data$medv[indices],
family = "gaussian", alpha = 1, lambda = 0.1)
return(fit$beta)
}
# Train multiple base models using bootstrapping and store each set of coefficients
coefficients <- NULL
for (i in 1:10) {
bootstrapped_indices <- sample(1:nrow(train), replace = TRUE)
coefficients[[i]] <- base_model(train, bootstrapped_indices)
}
# Convert list into a matrix where each row represents the coefficients of a base model
coefficients_matrix <- t(do.call(cbind, coefficients))
# Average the coefficients to get the final model
final_coefficients <- as.matrix(colMeans(coefficients_matrix),
length(coefficients[[1]]))
round(final_coefficients,2)## [,1]
## crim -0.05
## zn 0.03
## indus -0.03
## chas 3.61
## nox -9.60
## rm 3.98
## age 0.00
## dis -1.03
## rad 0.12
## tax 0.00
## ptratio -0.89
## black 0.01
## lstat -0.57Let’s compare that with the coefficients of a regular lasso regression model:
## 13 x 1 sparse Matrix of class "dgCMatrix"
## s0
## crim -0.07
## zn 0.03
## indus -0.01
## chas 3.03
## nox -13.40
## rm 3.69
## age .
## dis -1.20
## rad 0.15
## tax 0.00
## ptratio -0.92
## black 0.01
## lstat -0.57Which model performs better for the test data set?
# Make predictions on the test set using the final model
predictions <- as.matrix(as.matrix(test[, -14]) %*% final_coefficients)
# Calculate the mean squared error
mean((predictions - test$medv)^2)## [1] 875.6266# Make predictions on the test set using the base model
base_predictions <- as.matrix(as.matrix(test[, -14]) %*% base_model(train, 1:nrow(train)))
# Calculate the mean squared error
mean((base_predictions - test$medv)^2)## [1] 1157.3685.3.2 Random forests
Random forests are an ensemble learning method that builds multiple decision trees during training and outputs the mode of the classes (classification) or the average prediction (regression) of the individual trees. The method is very much related to bagged decision trees. However, random forests introduce extra randomness into the tree-building process to make the model more robust. Here’s how random forests work:
Create bootstrap samples: Random forests start by generating multiple random samples (with replacement) from the original training data. These samples, called bootstrap replicates, are used to train individual decision trees.
Random feature selection: When building each decision tree, a random subset of features is selected as candidates for splitting at each node. This introduces diversity into the trees and helps to prevent overfitting.
Grow multiple trees: Multiple decision trees are grown using the bootstrap samples and random feature selection. Each tree is trained independently of the others.
Aggregate predictions: For regression tasks, the predictions from all the trees are averaged to get the final prediction. For classification tasks, the mode of the classes predicted by the individual trees is taken as the final prediction.
Out-of-bag evaluation: Random forests use out-of-bag (OOB) samples, which are data points not included in the bootstrap sample used to train each tree. These OOB samples can be used to estimate the model’s performance without the need for a separate validation set.
Random forests are known for their robustness, scalability and ability to handle high-dimensional data. By combining the predictions of multiple trees trained on different subsets of the data, random forests can produce accurate and stable models for a wide range of machine learning tasks.
Out-of-bag samples are data points that are not included in the bootstrap sample used to train a particular tree. These samples can be used to estimate the performance of the model without the need for a separate validation set. The out-of-bag error is calculated by aggregating the predictions of the trees that did not use a particular data point in their training. This provides an unbiased estimate of the model’s performance on unseen data and can be useful for small datasets where cross-validation may be impractical.
Figures 5.3 and 5.4 illustrate the two phases of employing random forests: the training phase and the prediction phase.
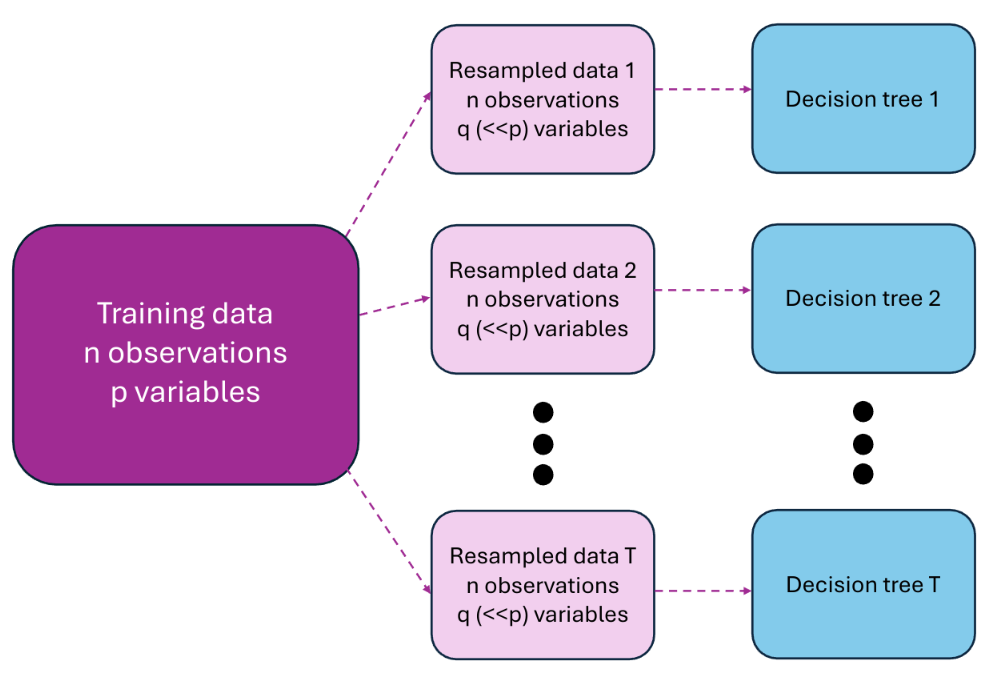
Figure 5.3: Training of random forests
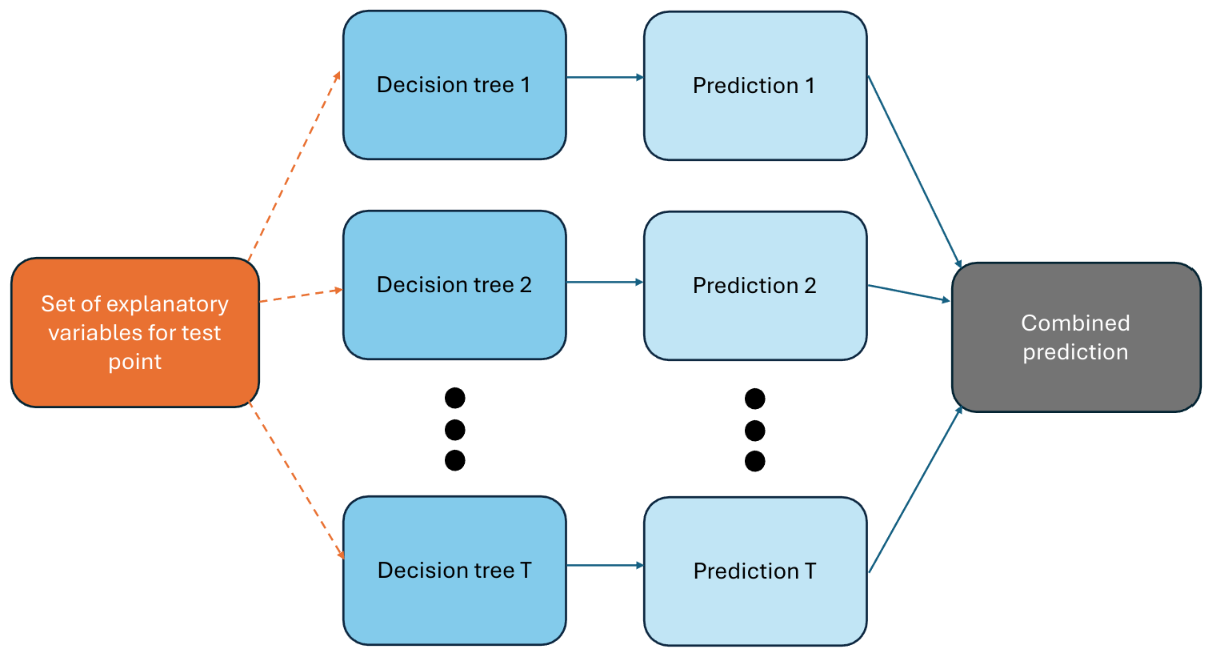
Figure 5.4: Predicting with random forests
Example
In R, we can use the randomForest package to build a random forest model. Here’s an example using the iris dataset:
# Load the required library
library(randomForest)
# Load the iris dataset
data(iris)
# Create a training and test set using the sample function
set.seed(123)
train_index <- sample(1:nrow(iris), 0.8 * nrow(iris))
train <- iris[train_index, ]
test <- iris[-train_index, ]
# Train a random forest model
rf_model <- randomForest(Species ~ .,
data = train,
ntree = 500)
# Make predictions on the test set
rf_predictions <- predict(rf_model, newdata = test)
# Evaluate the performance of the model
confusionMatrix(test$Species, rf_predictions)$table## Reference
## Prediction setosa versicolor virginica
## setosa 10 0 0
## versicolor 0 14 1
## virginica 0 0 5Let’s compare that with bagged decision trees:
# Train a bagged decision tree model
bagged_model <- randomForest(Species ~ ., data = train,
ntree = 500,
mtry = ncol(train) - 1)
# Make predictions on the test set
bagged_predictions <- predict(bagged_model,
newdata = test)
# Evaluate the performance of the model
confusionMatrix(test$Species, bagged_predictions)$table## Reference
## Prediction setosa versicolor virginica
## setosa 10 0 0
## versicolor 0 14 1
## virginica 0 0 5Notice that the R function randomForest can be used to build both random forests and bagged decision trees. The difference between the two lies in the mtry parameter, which controls the number of features randomly selected at each split. In random forests, mtry is set to the square root of the total number of features by default, while in bagged decision trees, it is set to the total number of features.
Example
It is instructive to code a random forest (almost) from scratch. Here is an example of a random forest for the iris dataset using the rpart package:
# Load the required library
library(rpart)
# Load the iris dataset
data(iris)
# Create a training and test set using the sample function
set.seed(123)
train_index <- sample(1:nrow(iris), 0.8 * nrow(iris))
train <- iris[train_index, ]
test <- iris[-train_index, ]
# Train multiple decision trees
ntrees <- 500
trees <- list()
for (i in 1:ntrees) {
# Create a bootstrap sample
bootstrap <- sample(1:nrow(train), replace = TRUE)
train_bootstrap <- train[bootstrap, ]
# Train a decision tree on the bootstrap sample
tree <- rpart(Species ~ ., data = train_bootstrap, method = "class")
trees[[i]] <- tree
}
# Make predictions on the test set
predictions <- matrix(0, nrow = nrow(test), ncol = ntrees)
for (i in 1:ntrees) {
predictions[, i] <- predict(trees[[i]],
newdata = test,
type = "class")
}
# Aggregate the predictions
final_predictions <- apply(predictions, 1, function(x) {
names(sort(table(x), decreasing = TRUE)[1])
})
# Convert the predictions of "1", "2", "3" to
# "setosa", "versicolor", "virginica"
final_predictions_ <- factor(final_predictions,
levels = c("1", "2", "3"),
labels = c("setosa",
"versicolor",
"virginica"))
# Evaluate the performance of the model
confusionMatrix(test$Species, final_predictions_)$table## Reference
## Prediction setosa versicolor virginica
## setosa 10 0 0
## versicolor 0 14 1
## virginica 0 0 5In the “Aggregate the predictions” step, we use a majority vote to determine the final prediction for each data point. The class with the most votes from the individual trees is chosen as the final prediction. This is a common approach in random forests and helps to reduce the variance of the model. You might find it helpful to play with the function in the apply function to see how the predictions are determined.
5.3.2.1 Optimisation for random forest fitting
The randomForest package in R provides a number of parameters that can be tuned to optimise the performance of the model. Some of the key parameters include:
ntree: The number of trees to grow in the forest. Increasing the number of trees can improve the model’s performance but also increases the computational cost.mtry: The number of features randomly selected at each split. A smallermtryvalue can increase the diversity of the trees and reduce overfitting.nodesize: The minimum size of terminal nodes. A largernodesizevalue can prevent the trees from growing too deep and overfitting the data.sampsize: The number of samples randomly selected for each tree. A smallersampsizevalue can increase the diversity of the trees and reduce overfitting.
By tuning these parameters, you can optimise the performance of the random forest model for your specific dataset and task. Random forests are fitted using indivually optimised decision trees as discussed in the section on decision trees in Chapter 3.
5.4 Boosting
Boosting is yet another powerful ensemble method in machine learning that focuses on improving the accuracy of predictions by sequentially training weak learners into a single, strong learner. Unlike bagging, which trains base learners in parallel, boosting trains them sequentially, with each new learner learning from the mistakes of its predecessors. Here’s how boosting works:
- Train weak learners iteratively: Boosting starts by training a weak learner on the entire dataset. A weak learner is a simple model that performs only slightly better than random guessing.
- Focus on errors: After the first weak learner is trained, the algorithm identifies the data points that the model incorrectly predicted. These points are then given higher importance (weight) in the next iteration.
- Train subsequent learners: A new weak learner is trained using the adjusted weights, focusing on the previously misclassified examples. This process continues iteratively, with each new learner trying to improve upon the performance of the previous ones.
- Combine predictions: Finally, the predictions from all the weak learners are combined, typically using a weighted voting scheme where better performing learners have more influence. The combined prediction from the ensemble is the final output of the boosting model.
By strategically focusing on the hard-to-learn examples and leveraging a team of weak learners, boosting helps create a more robust and accurate final model compared to any single weak learner.
5.4.1 AdaBoost
AdaBoost (Adaptive Boosting) is one of the most popular boosting algorithms that has been widely used in practice. It was introduced by Yoav Freund and Robert Schapire in 1996. AdaBoost works by combining multiple weak learners to create a strong learner. The key idea behind AdaBoost is to assign weights to the training examples and adjust these weights at each iteration to focus on the misclassified examples.
In R, we can use the adabag package to implement AdaBoost. Here’s an example using the iris dataset:
# Load the required library
library(adabag)
# Load the iris dataset
data(iris)
# Create a training and test set using the sample function
set.seed(123)
train_index <- sample(1:nrow(iris), 0.8 * nrow(iris))
train <- iris[train_index, ]
test <- iris[-train_index, ]
# Train an AdaBoost model
ada_model <- boosting(Species ~ ., data = train,
boos = TRUE, mfinal = 500)
# Make predictions on the test set
ada_predictions <- predict(ada_model, newdata = test)
# Convert the predictions in ada_predictions$class to a factor
ada_predictions$class <- factor(ada_predictions$class,
levels = c("setosa",
"versicolor",
"virginica"))
# Evaluate the performance of the model
confusionMatrix(test$Species,
ada_predictions$class)$table## Reference
## Prediction setosa versicolor virginica
## setosa 10 0 0
## versicolor 0 14 1
## virginica 0 0 5The function boosting from the adabag package is used to train an AdaBoost model. The boos parameter is set to TRUE to indicate that AdaBoost should be used. The mfinal parameter specifies the maximum number of iterations (weak learners) to train.
5.4.2 XGBoost
XGBoost (Extreme Gradient Boosting) is an advanced implementation of the gradient boosting algorithm that has gained popularity in recent years. Developed by Tianqi Chen and Carlos Guestrin in 2016, XGBoost is known for its speed, performance, and scalability. It has been widely used in machine learning competitions and real-world applications.
In R, we can use the xgboost package to implement XGBoost. Here’s an example using the iris dataset:
# Load the required library
library(xgboost)
# Load the iris dataset
data(iris)
# Create a training and test set using the sample function
set.seed(123)
train_index <- sample(1:nrow(iris), 0.8 * nrow(iris))
train <- iris[train_index, ]
test <- iris[-train_index, ]
# Convert label to numeric
train$Species <- as.numeric(train$Species) - 1
# Convert the data to a DMatrix object
dtrain <- xgb.DMatrix(data = as.matrix(train[, -5]),
label = train$Species)
dtest <- xgb.DMatrix(data = as.matrix(test[, -5]),
label = test$Species)
# Train an XGBoost model
xgb_model <- xgboost(data = dtrain, nrounds = 500,
objective = "multi:softmax",
num_class = 3)
# Make predictions on the test set
xgb_predictions <- predict(xgb_model, dtest)
# Convert the predictions to original class labels
xgb_predictions <- ifelse(xgb_predictions == 0, "setosa",
ifelse(xgb_predictions == 1,
"versicolor", "virginica"))
xgb_predictions <- factor(xgb_predictions,
levels = c("setosa",
"versicolor",
"virginica"))## Reference
## Prediction setosa versicolor virginica
## setosa 10 0 0
## versicolor 0 14 1
## virginica 0 0 5The conversion of the data to a DMatrix object is required for training an XGBoost model because the algorithm is optimised for this data structure. The nrounds parameter specifies the number of boosting rounds (iterations) to train. The objective parameter specifies the loss function to be optimised, and num_class specifies the number of classes in the dataset. In this example, we use the “softmax” objective for multiclass classification. Mathematically, the softmax function is defined as:
\[ \text{softmax}(x_i) = \frac{e^{x_i}}{\sum_{j=1}^{N} e^{x_j}} \]
where \(x_i\) is the input to the function and \(N\) is the number of classes. The rationale behind using the softmax function is to convert the raw output of the model into probabilities that sum to one. As discussed earler, this translates a deterministic output into a probability that the data point belongs to a particular class.
5.5 Error-Correcting Output Codes
Error-Correcting Output Codes (ECOC) is a technique used in multiclass classification to improve the performance of an ensemble of binary classifiers. The idea behind ECOC is to represent each class as a unique binary code and train multiple binary classifiers to distinguish between the different classes based on these codes.
Here’s how ECOC works in the training phase:
- Code Matrix Construction: Construct a code matrix where each row represents a class and each column represents an independent binary classifier. The entries in the matrix are typically -1, 0, or 1, where -1 and 1 indicate the two classes for the binary classifier, and 0 indicates that the classifier does not consider that class.
- Binary Classifier Training: We train the binary classifiers using the binary codes as the target variable.
And in the prediction phase:
- Prediction: For a new instance, each binary classifier makes a prediction resulting in a sequence of -1 and 1 (and possibly 0).
- Codeword Matching: The predicted binary vector is compared to the codewords in the code matrix. The class with the closest codeword is selected as the predicted class.
For the codeword matching, the Hamming distance is often used as a measure of similarity between the predicted binary vector and the codewords. The class with the codeword that has the smallest Hamming distance to the predicted vector is chosen as the final prediction.
Example
Let’s consider an example where we have three classes. If M1 denotes the first binary classifier for example, our code matrix could look like this:
| Class | M1 | M2 | M3 |
|---|---|---|---|
| A | -1 | -1 | 0 |
| B | 1 | 0 | -1 |
| C | 0 | 1 | 1 |
We could add in further redundancy to the code matrix to improve the performance of the model.
| Class | M1 | M2 | M3 | M4 | M5 | M6 |
|---|---|---|---|---|---|---|
| A | -1 | -1 | 0 | 1 | 1 | 0 |
| B | 1 | 0 | -1 | 0 | 1 | 1 |
| C | 0 | 1 | 1 | -1 | 0 | -1 |
Imagine that we have a new instance that is predicted by the binary classifiers as:
| M1 | M2 | M3 | M4 | M5 | M6 |
|---|---|---|---|---|---|
| -1 | 1 | 1 | 1 | 0 | -1 |
The Hamming distance between this vector and the codewords in the code matrix is:
| Class | Hamming Distance |
|---|---|
| A | 4 |
| B | 6 |
| C | 2 |
Therefore, the predicted class would be C.
Example
We can use base R to implement Error-Correcting Output Codes after we have fitted our individual models. Here’s an example using the iris dataset and three separate decision tree classifiers:
library(rpart)
library(rpart.plot)
library(MASS)
# Load the iris dataset
data(iris)
# Encode classes as binary codes for the six models
iris$o1 <- as.factor(ifelse(iris$Species == "setosa", 1,
ifelse(iris$Species == "versicolor",
-1, 0)))
iris$o2 <- as.factor(ifelse(iris$Species == "setosa", 1,
ifelse(iris$Species == "virginica",
-1, 0)))
iris$o3 <- as.factor(ifelse(iris$Species == "versicolor", 1,
ifelse(iris$Species == "virginica",
-1, 0)))
iris$o4 <- iris$o1
iris$o5 <- iris$o2
iris$o6 <- iris$o3
# Set-up the code matrix corresponding to these binary classifiers
code_matrix <- matrix(c(1, 1, 0, 1, 1, 0,
-1, 0, 1, 1, 0, 1,
0, -1, -1, 0, -1, -1),
nrow = 3, byrow = TRUE)
# Create a training and test set using the sample function
set.seed(123)
train_index <- sample(1:nrow(iris), 0.8 * nrow(iris))
train <- iris[train_index, ]
test <- iris[-train_index, ]
# Train multiple binary classifiers
M1 <- rpart(o1 ~ Sepal.Length+Sepal.Width+
Petal.Length+Petal.Width,
data = train[train$o1 != "0",], method = "class")
M2 <- rpart(o2 ~ Sepal.Length+Sepal.Width+
Petal.Length+Petal.Width,
data = train[train$o2 != "0",], method = "class")
M3 <- rpart(o3 ~ Sepal.Length+Sepal.Width+
Petal.Length+Petal.Width,
data = train[train$o3 != "0",], method = "class")
M4 <- lda(o4 ~ Sepal.Length+Sepal.Width+
Petal.Length+Petal.Width,
data = train[train$o4 != "0",])
M5 <- lda(o5 ~ Sepal.Length+Sepal.Width+
Petal.Length+Petal.Width,
data = train[train$o5 != "0",])
M6 <- lda(o6 ~ Sepal.Length+Sepal.Width+
Petal.Length+Petal.Width,
data = train[train$o6 != "0",])
# Make predictions on the test set
pred1 <- predict(M1, newdata = test, type = "class")
pred2 <- predict(M2, newdata = test, type = "class")
pred3 <- predict(M3, newdata = test, type = "class")
pred4 <- predict(M4, newdata = test)$class
pred5 <- predict(M5, newdata = test)$class
pred6 <- predict(M6, newdata = test)$class
# Combine the predictions into a data frame
stacked_data <- data.frame(pred1, pred2, pred3,
pred4, pred5, pred6)
# Compare each row of the stacked data to the code matrix
# and calculate the Hamming distance
hamming_distances <- apply(stacked_data, 1, function(x) {
apply(code_matrix, 1, function(y) sum(x != y))
})
# Determine the predicted class based on the
# minimum Hamming distance
predicted_classes <- apply(hamming_distances, 2, function(x) {
which.min(x)
})
# Convert the predicted classes to the original class labels
predicted_classes <- factor(ifelse(predicted_classes == 1,
"setosa",
ifelse(predicted_classes == 2,
"versicolor", "virginica")),
levels = c("setosa",
"versicolor", "virginica"))
# Evaluate the performance of the model
table(test$Species,
predicted_classes)## predicted_classes
## setosa versicolor virginica
## setosa 10 0 0
## versicolor 0 13 2
## virginica 0 0 5Let’s compare the performance of the ECOC model with a regular random forest model:
# Train a random forest model
rf_model <- randomForest(Species ~ Sepal.Length+Sepal.Width+
Petal.Length+Petal.Width,
data = train, ntree = 500)
# Make predictions on the test set
rf_predictions <- predict(rf_model, newdata = test)
# Evaluate the performance of the model
table(test$Species,
rf_predictions)## rf_predictions
## setosa versicolor virginica
## setosa 10 0 0
## versicolor 0 14 1
## virginica 0 0 5With far fewer models, we have achieved a similar performance to the random forest model.
5.6 Other ensemble methods
There are many other ensemble methods in machine learning that leverage the power of combining multiple models to improve performance. Some other popular ensemble methods include:
- Voting: In voting, multiple models are trained independently, and their predictions are combined using a majority vote (classification) or averaging (regression).
- Blending: Blending is similar to stacking but uses a separate validation set to train the meta-model.
- Bayesian model averaging: Bayesian model averaging combines the predictions of multiple models using Bayesian inference to estimate the model weights.
- Hierarchical ensembles: Hierarchical ensembles combine multiple levels of ensembles to create a more complex model.
Each ensemble method has its strengths and weaknesses, and the choice of method depends on the specific problem at hand.
The question remains as to why we would use ensemble methods and why we don’t just utilise the best model. The answer is that ensemble methods can often outperform individual models by leveraging the diversity of multiple models. It is often easier to get a richer model by combining simple models rather than trying to build a complex model from scratch. By combining the predictions of different models, ensemble methods can reduce the risk of overfitting, improve the robustness of the model, and achieve better generalisation on unseen data.