Topic 2 - Complex Numbers

2.0 Introduction

Complex numbers provide a way of working with equations such as $x^2=-7$ that don’t have solutions in the ordinary real numbers we are used to.

Their very special properties can simplify the study of areas such as geometry, particle physics, fluid mechanics, electrical circuits,… which don’t initially appear to need a square root of $-1$. But why should such a curious thing ever arise?

There are good reasons for introducing new types of “numbers” - to solve equations. It’s natural to start with the set of natural numbers, which we write as \[ \mathbb{N} = \left\{1,2,3,...\right\} \] We have no problem adding and multiplying them: given $a,b\in\mathbb{N}$, we can find $c,d\in\mathbb{N}$ satisfying \[c=a+b\qquad\text{and}\qquad d=ab.\] However, if we want to always find an $x$ satisfying \[a+x=b,\] we are led to introduce negative numbers. We thus get the set of integers (whole numbers) \[\mathbb{Z}=\left\{...,-2,-1,0,1,2,...\right\} \] If we further want to always find an $x$ so that \[bx=a\] (at least for $b\neq 0$), we are led to the rational numbers $\mathbb{Q}$, i.e. fractions of integers. We can add, subtract, multiply and divide (except by $0$) these just fine.

But then what about equations such as $x^2=2$?

$\,$

Theorem. $\,$ The number $\sqrt{2}$ is not in $\mathbb{Q}$.

Just for fun, let’s actually prove this. Suppose on the contrary that $\;\sqrt{2}\;$ is rational. Then there are positive integers $a,b$ with no common integer factors such that \[\sqrt{2}=\dfrac{a}{b},\qquad\text{i.e.}\qquad a^2=2b^2.\] But this means $a^2$ and hence $a$ is an even number, so $a=2c$ for some integer $c$. The above now says \[a^2=(2c)^2=2b^2\qquad\text{and so}\qquad b^2=2c^2.\] But now this means $b^2$ and hence $b$ is even. We have shown that both $a$ and $b$ are divisible by 2.
But we said that they had no common factor and so this contradiction means $a$ and $b$ can’t exist in the first place.

This reasoning (“proof by contradiction”) is very common in maths. A small modification of the above shows more generally that a natural number $m$ is either a perfect square or $\sqrt{m}$ is irrational.

$\,$

Thus, starting with the rationals, we can go on to create irrational numbers such as $\sqrt{2}$, $\sqrt[3]{2+\sqrt{7}}$,… which are not merely fractions of integers. However, there are numbers we are familiar with which are not even roots of polynomials with rational coefficients. These are the transcendental numbers and include the well-known numbers $\pi$ and $e$.

We can, however, think of $\pi$ as a “limit” of rational numbers, e.g. $3, 3.1, 3.14, 3.141,...$ which get progressively closer to $\pi$. By similar considerations (that we won’t go into), one can construct any of the real numbers $\mathbb{R}$. You can think of this as the set of numbers formed from (possibly infinite) decimal expansions, e.g. $e=2.7182818284...$.

Unfortunately, there are still some gaps. Some quadratic equations, e.g. $x^2-7=0$ have two solutions in $\mathbb{R}$ whereas others, e.g. $x^2+7=0$ have none. We fix this non-uniform behaviour by introducing the complex numbers. Complex numbers are of the form \[z=x+iy\] where $x$ and $y$ are real numbers and $i=\sqrt{-1}$ is a special new number satisfying $i^2=-1$. We use the symbol $\mathbb{C}$ to mean the set of all complex numbers, just as we use $\mathbb{Z}$ for the integers and $\mathbb{R}$ for the real numbers.

Mathematicians like complex numbers because, just by including $i=\sqrt{-1}$, we obtain the Fundamental Theorem of Algebra. This says that a polynomial equation of any degree \[ z^n + a_{n-1}z^{n-1} + \ldots + a_1z + a_0 = 0, \] where $a_0, a_1,\ldots, a_{n-1}$ are in $\mathbb{C}$, has exactly $n$ roots in $\mathbb{C}$ (up to multiplicity). In other words, there are unique roots $z_1, z_2,\ldots,z_n$ (not necessarily distinct) in $\mathbb{C}$ such that we can factorize \[ z^n + a_{n-1}z^{n-1} + \ldots + a_1z + a_0 = (z-z_1)(z-z_2)\cdots(z-z_n). \]

Even if the coefficients are real, it could be that the roots are not. But the theorem tells us that all polynomials have the ``correct’’ number of roots if we allow for complex numbers.

Example. $\,$ Consider the quadratic equation $z^2+7=0$. This is a polynomial equation with real coefficients, but the roots have the form \[ z = \pm\sqrt{-7} = \pm\sqrt{7}\sqrt{-1} = \pm i\sqrt{7}, \] which are not real. This corresponds to the factorisation \[z^2+7=(z+i\sqrt{7})(z-i\sqrt{7}).\]

$\,$

Notation: occasionally electrical engineers use the letter $j$ instead of $i$ because $i$ is often used for currents. But we will use the more common $i$.

$\,$

2.1 Complex Arithmetic

In this section, we will learn about the basic properties and manipulation of complex numbers, so that you are comfortable using them in other modules.

Given a complex number \[z=x+iy\] where $x$ and $y$ are real numbers, we call $x$ the real part and $y$ the imaginary part, and write \[ x = \operatorname{Re}(z), \qquad y = \operatorname{Im}(z). \] If $x=0$ we say that $z$ is purely imaginary and if $y=0$ then $z$ is just a real number.

Warning: $\,$ $\operatorname{Im}(z)$ is the real number $y$, not the imaginary number $iy$.

$\,$

Using their real and imaginary parts, complex numbers can be thought of geometrically as “numbers with two coordinates”. We can represent them by a position in two-dimensional space, called the complex plane or sometimes an Argand diagram. For example:

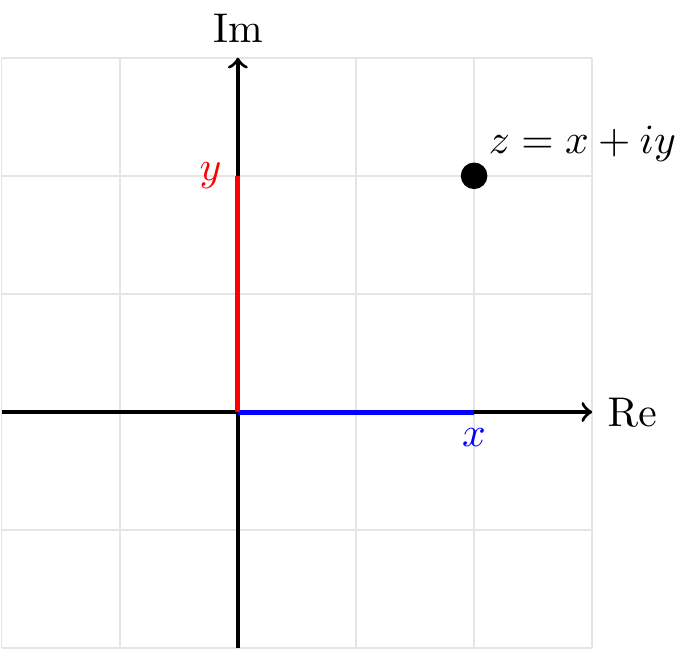
There are some basic rules for manipulating complex numbers.

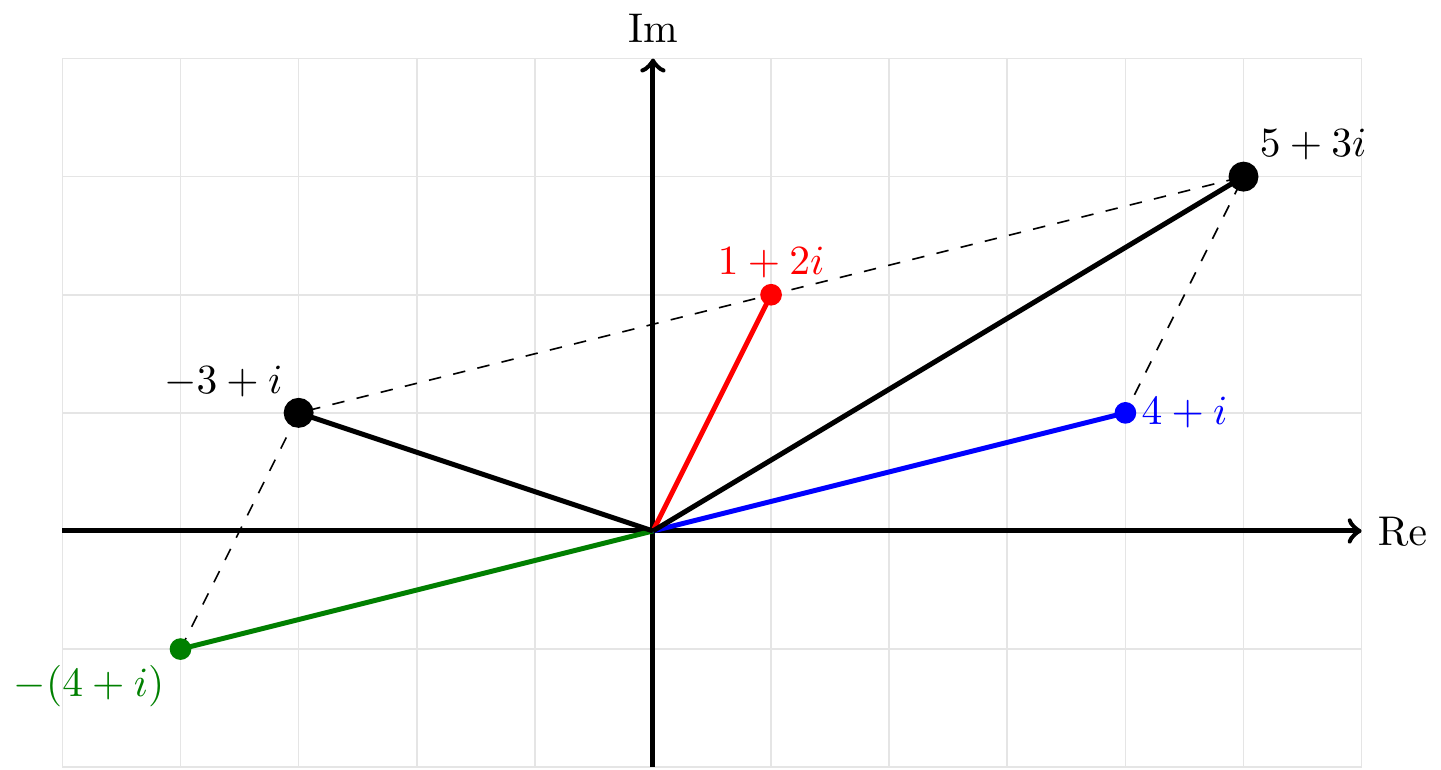
Addition and Subtraction:$\,$ We add and subtract two complex numbers by adding their corresponding real and imaginary parts. For example \[ \color{red}{(1 + 2i)} + \color{blue}{(4 + i)} = (\color{red}{1}+\color{blue}{4}) + i(\color{red}{2}+\color{blue}{1}) = 5 + 3i \] and \[ \color{red}{(1 + 2i)} - \color{blue}{(4 + i)} = (\color{red}{1}-\color{blue}{4}) + i(\color{red}{2}-\color{blue}{1}) = -3+i. \]

Notice that two complex numbers $z=x+iy$ and $w=u+iv$ are equal when \[\begin{align*} z = w \quad &\iff z - w = 0,\\ &\iff x-u=0 \quad\text{and}\quad y -v = 0,\\ &\iff x = u \quad\text{and}\quad y=v. \end{align*}\] In other words, they’re equal precisely when their real and imaginary parts are both equal.

In the complex plane, adding two complex numbers is like adding vectors (which we will come back to in Topic 3). For example, the sum and difference above look as follows:

$\,$

Complex conjugation: $\,$ Given $z=x+iy$, we define the complex conjugate of $z$ to be \[ \overline{z} = x - iy. \] In the complex plane, this is just the reflection of $z$ in the real axis:

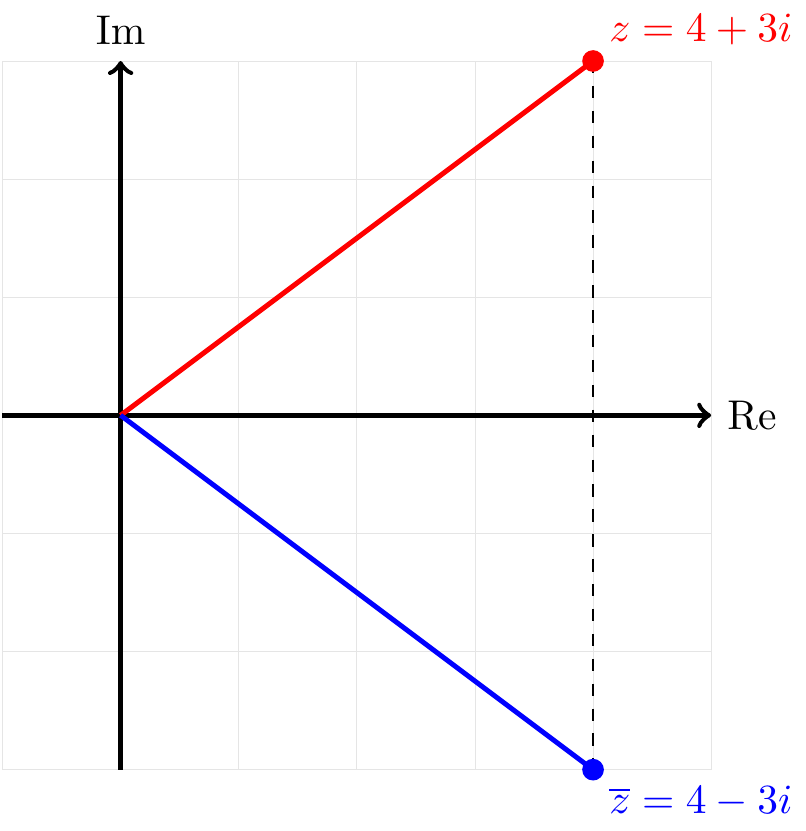
By combining $z$ and $\overline{z}$, we can derive expressions for the real and imaginary parts: \[\begin{align*} z + \overline{z} &= (x+iy) + (x-iy) = 2x = 2\operatorname{Re}(z) \quad\implies\quad \displaystyle\operatorname{Re}(z) = \frac{z + \overline{z}}{2},\\ z - \overline{z} &= (x+iy) - (x-iy) = 2iy = 2i\operatorname{Im}(z) \quad\implies\quad \displaystyle\operatorname{Im}(z) = \frac{z - \overline{z}}{2i}. \end{align*}\]

Multiplication: $\,$ We just use the normal rules of algebra, along with the fact that $i^2=-1$. For example, \[\begin{align*} (2+3i)(5+i) &= 2(5) + 2i + 3(5)i + 3i^2 = 10 + 2i + 15i + 3(-1) \\ &= 7 + 17i. \end{align*}\] Also, notice we actually have two square roots of $-1$ since $(-i)^2=i^2=-1$ as well.

The geometrical interpretation of multiplication is more complicated and we will return to it later…

Modulus: $\,$ For an arbitrary complex number $z=x+iy$, we have \[\begin{align*} z\overline{z} = (x+iy)(x-iy) = x^2 + y^2. \end{align*}\] This is a non-negative real number and is zero precisely when $z=0$. The modulus (or absolute value) of $z$ is defined by \[\begin{align*} |z| = \sqrt{z\overline{z}} = \sqrt{x^2 + y^2}. \end{align*}\] In the complex plane, this is the distance between the origin and $z$ (by Pythagoras):

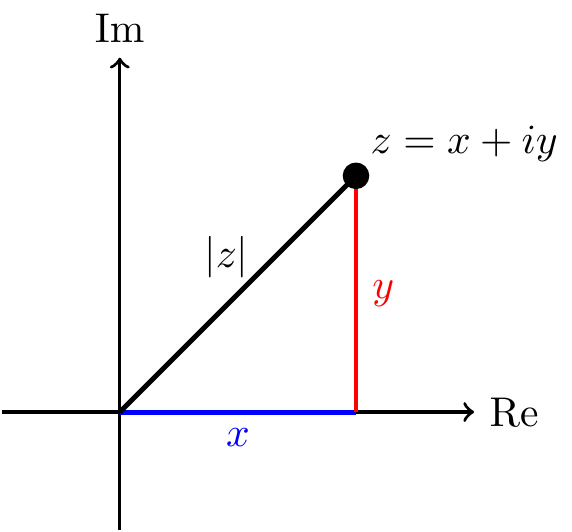
Division: $\,$ We can remove complex denominators from a fraction by multiplying top and bottom by the complex conjugate of the denominator. For example, \[\begin{align*} \frac{2+3i}{5+i} = \frac{(2+3i)(5-i)}{(5+i)(5-i)} &= \frac{2(5) - 2i + 3(5)i + 3}{5^2 + 1^2} \\ &= \frac{13 + 13i}{26} = \frac12 + \frac12i. \end{align*}\]

We can see from the definitions that complex conjugation combines nicely with arithmetic operations. In particular, you can check from the definitions that: \[\begin{align*} &\overline{z+w} = \overline{z} + \overline{w}, \quad\text{and}\quad \overline{z-w} = \overline{z} - \overline{w},\\ &\overline{zw} = \left(\overline{z}\right)\left(\overline{w}\right), \quad\text{and}\quad \displaystyle\overline{\left(\frac{z}{w}\right)} = \frac{\overline{z}}{\overline{w}}. \end{align*}\] These can make calculations much easier.

Example. $\,$ Find the complex conjugate of $(2 + 3i)^7$.

We have \[\overline{(2+3i)^7} = (\overline{2+3i})^7 = (2-3i)^7.\]

$\,$

A similar thing happens with the modulus – it works nicely with multiplication and division. Notice that \[ |zw|^2 = (zw)(\overline{zw}) = zw\overline{z}\,\overline{w} = z\overline{z}\,w\overline{w} = |z|^2|w|^2, \] and so $|zw| = |z|\,|w|$. Similarly, $\displaystyle\left|\frac{z}{w}\right| = \frac{|z|}{|w|}$.

Example. $\,$ $(i)\;\;$ Find the modulus of $(2 + 3i)^7$.

We have \[ |(2 + 3i)^7| = |2 + 3i|^7 = (\sqrt{2^2 + 3^2})^7 = 13^{7/2}. \]

$(ii)\;\;$ Find the modulus of $\dfrac{2+3i}{5+i}$.

We have \[\left|\frac{2+3i}{5+i}\right|=\frac{|2+3i|}{|5+i|} =\frac{\sqrt{2^2+3^2}}{\sqrt{5^2+1^2}}=\frac{\sqrt{13}}{\sqrt{26}}=\frac{\sqrt{2}}{2}. \] Notice we found this without using $\;\dfrac{2+3i}{5+i} = \dfrac12 + \dfrac12i$.

$\,$

Warning: $\,$ modulus does not work with addition and subtraction in the same way, and in general \[ |z+w| \neq |z| + |w|. \] This makes sense because geometrically, $|z|$, $|w|$ and $|z+w|$ are the three sides of a triangle:

The triangle inequality says that the length of any side of a triangle can not be greater than the sum of the other two side lengths.

Are there any triangles where one side length actually equals the sum of the other two? The answer is yes, but they are quite special and you might have to think about it to find them! We’ll return to the triangle inequality later.

$\,$

2.2 Polar Form

Polar coordinates lead to an important alternative way to represent complex numbers. Recall that a point with Cartesian coordinates $(x,y)$ has polar coordinates $(r,\theta)$ where \[ x = r\cos\theta \quad\text{and}\qquad y = r\sin\theta, \] so that \[ r = \sqrt{x^2 + y^2} \quad\text{and}\quad \tan\theta = \frac{y}{x}. \]

In the complex plane this looks like

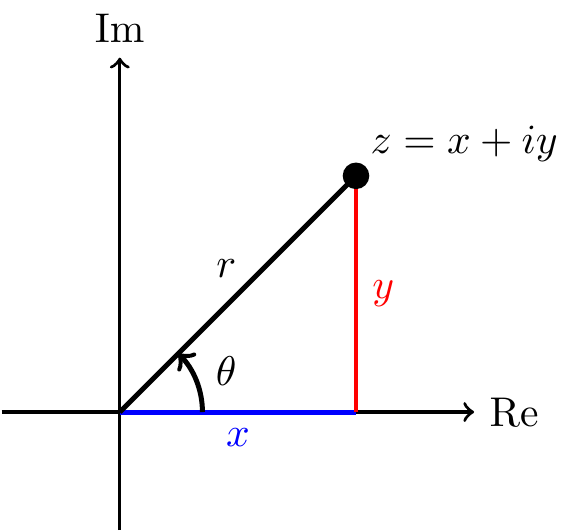
In terms of complex numbers, we have \[\begin{align*} z &= x+iy = r\cos\theta + ir\sin\theta = r(\cos\theta + i\sin\theta). \end{align*}\] As we saw earlier, the length \[r=|z|=\sqrt{x^2+y^2}\] is the modulus of $z$. The angle $\theta$ between the real axis and $z$ is called the argument of $z$ and written \[\theta=\arg(z).\]

Since shifting $\theta$ by a whole multiple of $2\pi$ doesn’t change $z$ (it just rotates a whole number of times around the origin) we can always make sure that $-\pi < \theta \leq \pi$. This particular value is called the principal argument and written $\operatorname{Arg}(z)$ with a capital letter. In general, we have $\arg(z) = \operatorname{Arg}(z) + 2n\pi$ for some $n\in\mathbb{Z}$.

We have to be careful when calculating $\theta$ from $x$ and $y$, because it is not simply $\theta = \arctan(y/x)$. The problem is that $\arctan$ gives values between $-\pi/2$ and $\pi/2$, but we want an angle which can be anything between $-\pi$ and $\pi$. We actually have $\theta=\arctan(y/x)$ or $\arctan(y/x) \pm \pi$, depending on which quadrant $z$ lies in. Most programming languages define a special function for this; in MATLAB you type atan2(y,x).

$\,$

Example. $\,$Find the moduli and principal arguments of $1+i$ and $-\sqrt{3}-i$.

(Note: “moduli” is the plural of modulus.)

The moduli are \[|1 + i| = \sqrt{1^2 + 1^2} = \sqrt{2}\] and \[|-\sqrt{3}-i| = \sqrt{(\sqrt{3})^2 + 1^2} = 2.\]

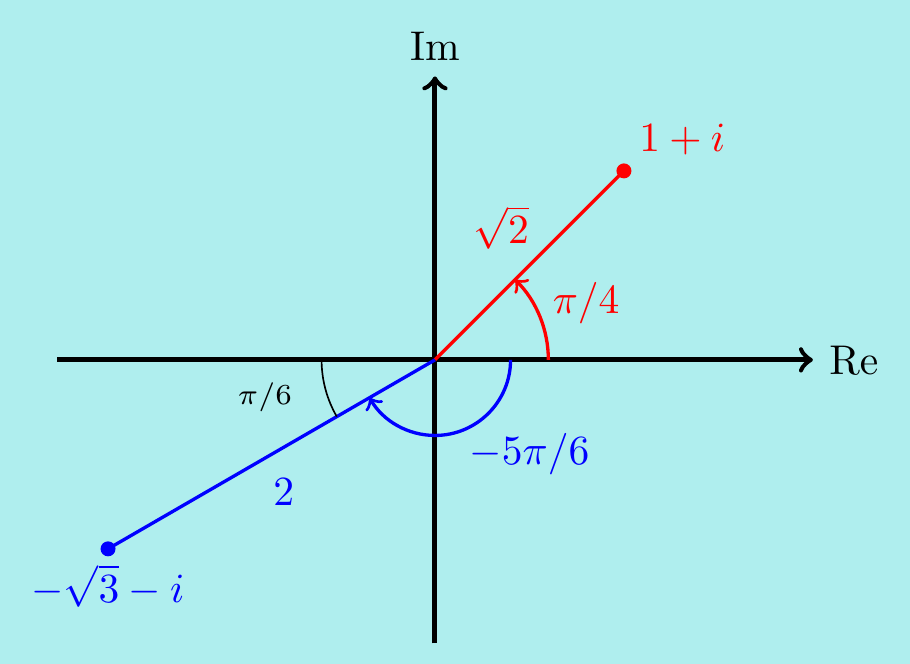
From the diagram, we have \[\operatorname{Arg}(1+i) = \arctan(1/1) = \pi/4\] and \[\operatorname{Arg}(-\sqrt{3}-i) = \arctan(1/\sqrt{3}) - \pi = -\pi+\pi/6 = -5\pi/6.\]

$\,$

Unless you have had lots of practice, always draw a picture to get the argument correct. I always do!

$\,$

It should be clear that two complex numbers are equal if and only if they have the same modulus and principal argument.

2.3 Euler’s Formula

A fundamental fact is \[ e^{i\theta} = \cos\theta + i\sin\theta. \] In particular, setting $\theta=\pi$ gives the famous equation \[ e^{i\pi} = -1. \]

This is often voted the most beautiful equation in all mathematics.

We can sketch of why Euler’s formula holds using some calculus. Suppose we define a function of a real number $\theta$, \[ f(\theta) = e^{-i\theta}(\cos\theta + i\sin\theta). \] We will show that this is always equal to 1. Treating $i$ as a regular number, the derivative is \[\begin{align*} f'(\theta) &= e^{-i\theta}(-\sin\theta + i\cos\theta) - ie^{-i\theta}(\cos\theta + i\sin\theta),\\ &= e^{-i\theta}(-\sin\theta + i\cos\theta - i\cos\theta - i^2\sin\theta)= 0. \end{align*}\] We have a function whose derivative is always zero and hence must be constant. However, \[f(0) = e^0(\cos0 + i\sin0) = 1,\] so $f(\theta)=1$ for all $\theta$ and Euler’s formula follows.

Any complex number can therefore be written as \[ z = x+ iy = re^{i\theta}. \]

With this representation, we can see what multiplication and division do geometrically in the complex plane. With $z=re^{i\theta}$ and $w=se^{i\phi}$, we have \[ zw = rse^{i(\theta+\phi)} \qquad \text{and} \qquad \frac{z}{w} = \frac{r}{s}e^{i(\theta-\phi)}. \] So when we multiply two complex numbers, we multiply their moduli and add their arguments. In other words, \[ |zw| = |z|\,|w| = rs \qquad \text{and} \qquad \arg(zw) = \arg(z) + \arg(w)=\theta+\phi. \]

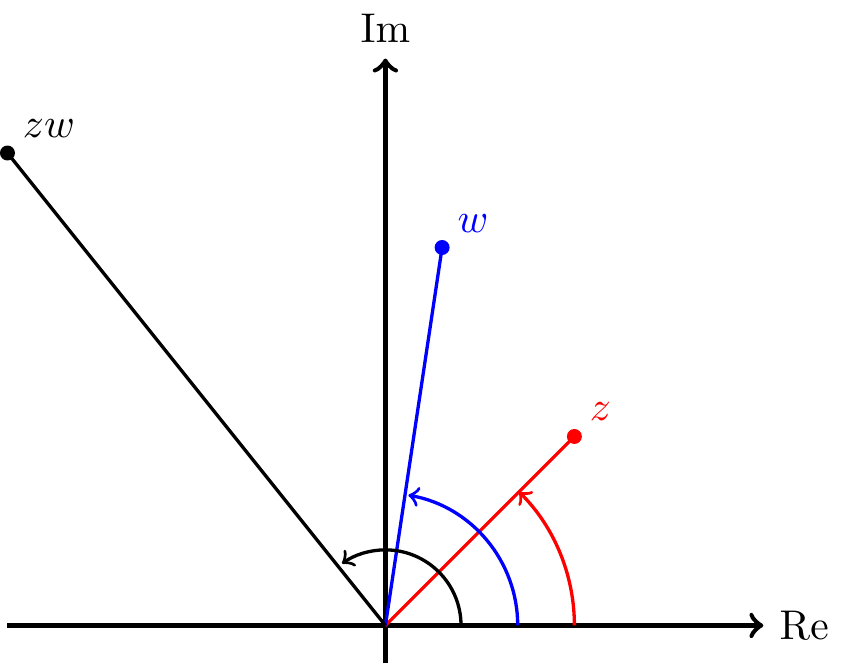
Generally speaking, Cartesian coordinates $x+iy$ are easy to add but complicated to multiply, whereas polar coordinates $re^{i\theta}$ are easy to multiply but complicated to add. We have to learn to choose whichever is most appropriate for the problem at hand.

2.4 Powers of Complex Numbers

If $z=re^{i\theta}$ and $a\in\mathbb{R}$, we can easily find \[ z^a = r^a(e^{i\theta})^a = r^ae^{ia\theta}. \] But remember that we can add a multiple of $2\pi$ to $\theta$ without changing $z$. So for any integer $n\in\mathbb{Z}$ we also have \[ z^a = r^ae^{ia\theta + 2an\pi i}. \] If $a$ is an integer, this makes no difference since $e^{2an\pi i}=1$. But if $a$ is non-integer, then $z^a$ will take multiple different values for different $n\in\mathbb{Z}$.

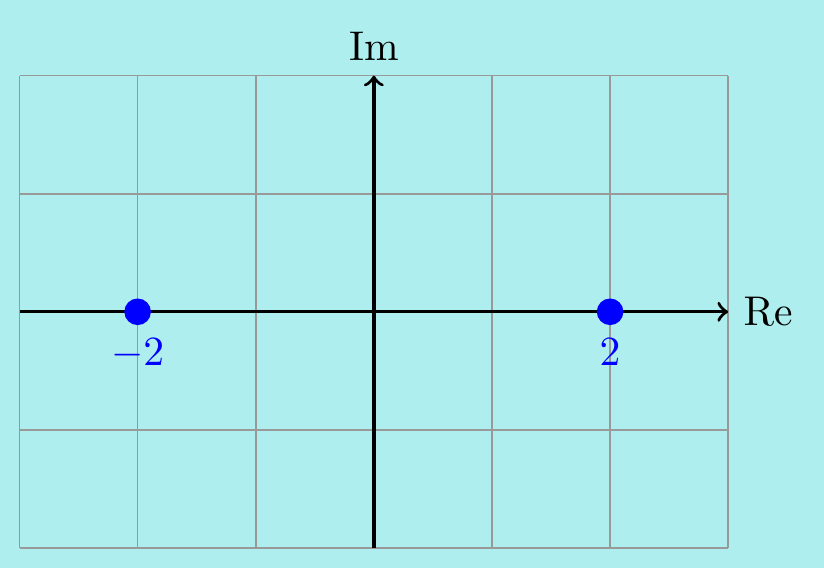
Example. $\,$ Let’s find all $z\in\mathbb{C}$ such that $z^2=4$. Notice that $z^2=4=4e^{2n\pi i}$ for any $n\in\mathbb{Z}$, and so \[ z = \left(4e^{2n\pi i}\right)^{1/2} = 4^{1/2}e^{n\pi i} = 2e^{n\pi i}. \] We have $e^{n\pi i}=1$ for even $n$ and $e^{n\pi i}=-1$ for odd $n$. So we get precisely the two real roots $z=\pm 2$ (that we should have already guessed).

Example. $\,$ Find all $z\in\mathbb{C}$ such that $z^3=1$. (These are the cube roots of 1.)

The Fundamental Theorem of Algebra says this should have three roots. However, only one of them is real, namely $z=1$ and the others must be complex! Writing $z^3=1=e^{2n\pi i}$, then \[ z = e^{2n\pi i/3} \quad \text{for $n\in\mathbb{Z}$}. \] There appear to be infinitely many solutions $\ldots, e^{-2\pi i/3}, e^0, e^{2\pi i/3},e^{4\pi i/3},\ldots$ but these actually repeat every third term, so there are exactly three roots \[ z = 1, e^{\pi i/3}, e^{-2\pi i/3}, \quad\textrm{that is,}\quad z = 1, \frac{-1\pm i\sqrt{3}}{2}. \]

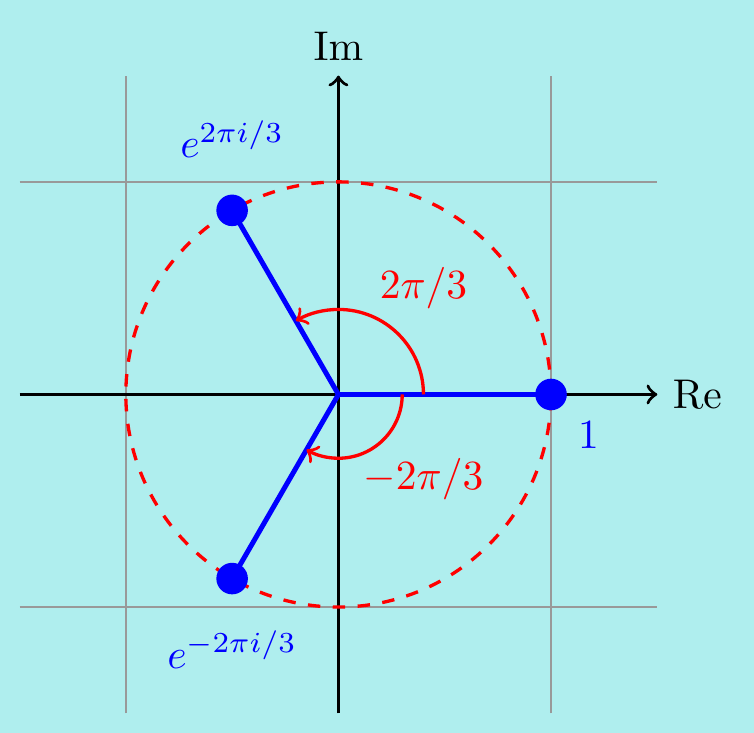
Notice these three cube roots of 1 lie at the corners of an equilateral triangle. We can deal with more general fractional powers in the same way: given $m\in\mathbb{Z}$ and $w\in\mathbb{C}$ solve \[z^m=w\] The key is to work with polar coordinates. Write $z=re^{i\theta}$ and $w=se^{i\phi}=se^{i\phi+2n\pi i}$. Then \[z^m=w\qquad\implies\qquad r^me^{im\theta}=se^{i\phi}=se^{i\phi+2n\pi i} \qquad\text{for any $n\in\mathbb{Z}$}\] and equating the modulus and argument on each side gives \[\begin{cases} r^m \!\!\!&=s \\ m\theta \!\!\!&=\phi+2n\pi \end{cases} \quad\implies\quad \begin{cases} r \!\!\!&=s^{1/m} \\ \theta \!\!\!&=\frac{\phi+2n\pi}{m} \end{cases} \quad\implies\quad z=s^{1/m}e^{i\phi/m+2n\pi i/m}\]
Notice shifting $n$ by a multiple of $m$ doesn’t change this so we do, as expected, get $m$ roots to the equation $z^m=w$, for example by taking $0\leq n\leq m-1$. In the complex plane, these are at the vertices of a regular polygon.

We can even raise a complex number to a complex power.

Example. $\,$ Again, we start by writing $i$ in polar coordinates. To find the argument draw the diagram:

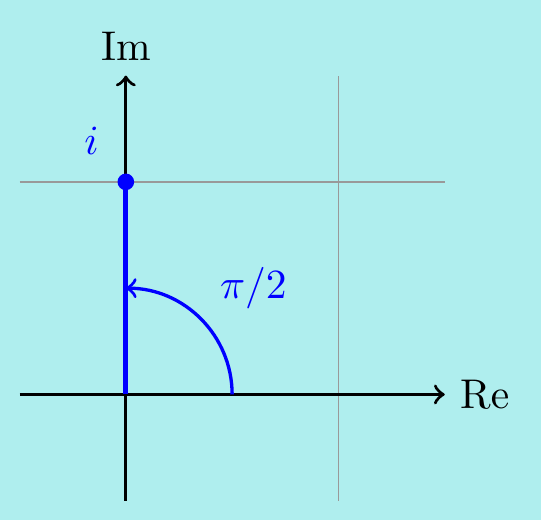
We see that $i = e^{\pi i/2} = e^{\pi i/2 + 2n\pi i}$ for any $n\in\mathbb{Z}$. Then \[ i^i = \Big(e^{\pi i/2 + 2n\pi i}\Big)^i = e^{\pi i^2/2 + 2n\pi i^2} = e^{-\pi i/2 - 2n\pi}. \] So \[ i^i = \ldots, e^{3\pi/2}, e^{-\pi/2}, e^{-5\pi/2},\ldots \] There are infinitely many solutions, and they are all real! For example, the three particular solutions listed are approximately $111.3, 0.2079, 0.00039$.

Here’s a more complicated example.

Example. $\,$ Find all values of $(1+i)^{2-i}$.

First, write $1+i$ in the appropriate form.

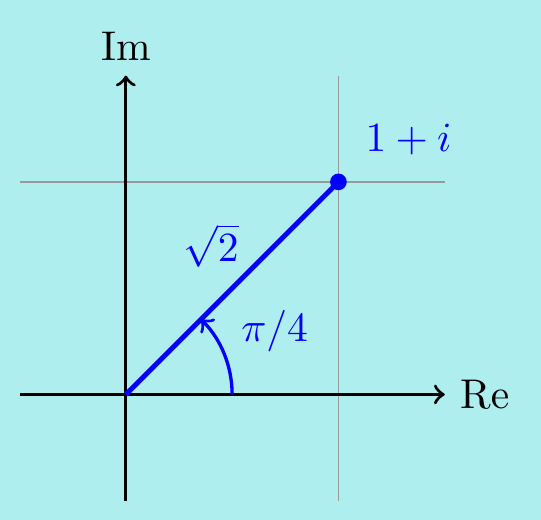
In polar form, we have $1+i = \sqrt{2}e^{\pi i/4} = \sqrt{2}e^{\pi i/4 + 2n\pi i}$ for any $n\in\mathbb{Z}$.

Also using $\sqrt{2} = e^{\ln\sqrt{2}}$, we can now write \[ 1 + i = e^{\ln\sqrt{2} + \pi i/4 + 2n\pi i}. \] for any $n\in\mathbb{Z}$. So \[\begin{align*} (1+i)^{2-i} &= e^{\left(\ln\sqrt{2} + \pi i/4 + 2n\pi i\right)(2-i)}\\ &= e^{\ln2 + \pi/4 + 2n\pi + i(\pi/2 - \ln\sqrt{2})+4n\pi i}\\ &= 2e^{\pi/4 + 2n\pi}e^{i(\pi/2 - \ln\sqrt{2})} \end{align*}\] where we have used $e^{4n\pi i}=1$ to simplify at the end. There are infinitely many values having a different modulus $2e^{\pi/4 + 2n\pi}$ for each $n\in\mathbb{Z}$ but having the same argument $\frac12\pi - \ln\sqrt{2}$. This means they all lie on a line through the origin in the complex plane.

More generally, to find $z^{a+ib}$ where $a,b$ are real, first write $z=re^{i\theta}$ in polar form.

Then using $r=e^{\ln{r}}$, we have \[z=e^{\ln{r}+i\theta}=e^{\ln{r}+i\theta+2n\pi i} \quad\text{for any $n\in\mathbb{Z}$.}\] Hence \[\begin{align*} z^{a+ib}=\left(e^{\ln{r}+i\theta+2n\pi i}\right)^{a+ib} &=e^{\left(\ln{r}+i\theta+2n\pi i\right)\left(a+ib\right)} \\ &=e^{a\ln{r}-b\left(\theta+2n\pi\right)+i\left(b\ln{r}+a\theta+2an\pi\right)} \\ &=\underbrace{r^ae^{-b(\theta+2n\pi)}}_{\text{modulus}}\;\;\;\; \overbrace{\!\!\!\!\!e^{i\left(b\ln{r}+a\theta+2an\pi\right)}}^{\text{argument}} \end{align*}\] Typically, one gets a different value for each $n\in\mathbb{Z}$.

Don’t memorise formulas like this or just substitute numbers into it! Instead, remember the method - write $z$ in the form $e^{\alpha+i\beta}$ then multiply out the powers and simplify.

2.5 Solving Polynomial Equations

Even though the Fundamental Theorem of Algebra tells us that polynomial equations always have complex solutions, we can only find explicit solutions in special cases. For example, we saw how to find all solutions to $z^m=w$ when $m$ is an integer.

Another special case we are familiar with is a quadratic equation \[ az^2 + bz + c = 0 \qquad \text{for $a, b, c\in\mathbb{C}$ and $a\neq 0$}. \] Remember that we solve this by completing the square: \[\begin{align*} az^2 + bz + c = 0 &\iff z^2 + \frac{b}{a}z + \frac{c}{a} = 0\\ &\iff \left( z + \frac{b}{2a}\right)^2 + \frac{c}{a} - \frac{b^2}{4a^2} = 0\\ &\iff \left( z + \frac{b}{2a}\right)^2 = \frac{b^2 - 4ac}{4a^2}\\ &\iff (2az + b)^2 = b^2 - 4ac. \end{align*}\] We know that $b^2-4ac$ has two square roots (even when $a,b,c$ are not real), so we obtain the usual formula \[ z = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}. \]

It’s also possible to deal with quadratic equations in $z^m$.

Example. $\,$ The Fundamental Theorem of Algebra tells us there should be six solutions. The key thing here is to notice that the polynomial is just a quadratic in $w=z^3$. So there are two solutions for $w$: \[ w^2 + 2w + 2 = 0 \quad\implies\quad w = \frac{-2 \pm\sqrt{2^2 - 4(1)(2)}}{2} = -1 \pm i. \] For each $w$, we can now find three solutions for $z$.

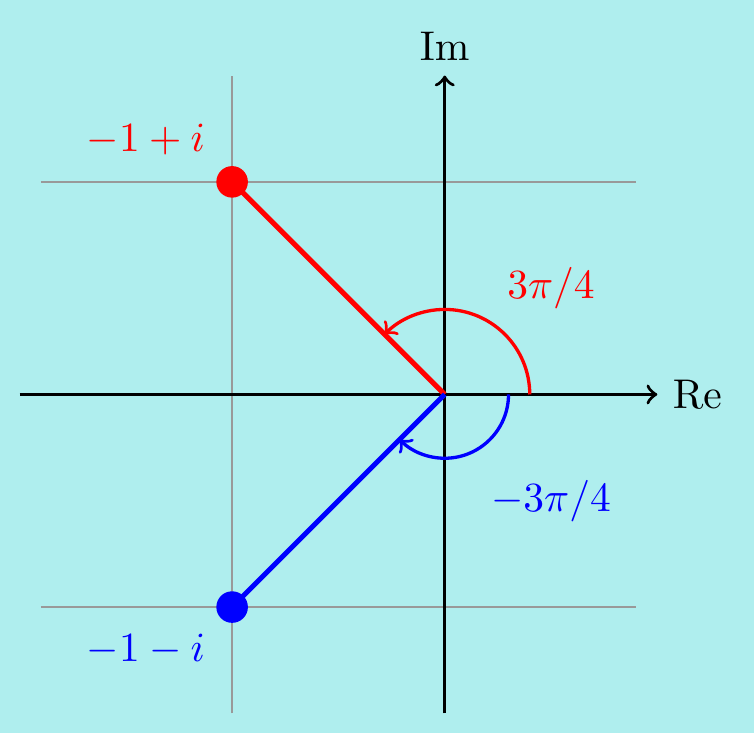
Firstly, converting $z^3=-1+i$ to polar coordinates gives \[\begin{align*} z^3 &= -1 + i = 2^{1/2}e^{3\pi i/4 + 2n\pi i} \quad\text{for $n\in\mathbb{Z}$}\\[5pt] \implies\quad z &= 2^{1/6}e^{\pi i/4 + 2n\pi i/3}. \end{align*}\] Taking three consecutive values for $n$ (e.g. $n=0,\pm1$) gives $z=2^{1/6}e^{\pi i/4}, 2^{1/6}e^{11\pi i/12}, 2^{1/6}e^{-5\pi i/12}$.

Similarly, $z^3 = -1-i$ gives \[\begin{align*} z^3 &= -1 - i = 2^{1/2}e^{-3\pi i/4 + 2n\pi i} \quad\text{for $n\in\mathbb{Z}$}\\[5pt] \implies\quad z &= 2^{1/6}e^{-\pi i/4 + 2n\pi i/3}, \end{align*}\] leading to the distinct solutions $z=2^{1/6}e^{-\pi i/4}, 2^{1/6}e^{5\pi i/12}, 2^{1/6}e^{11\pi i/12}$.

In summary, there are six solutions $z=2^{1/6}e^{\pm\pi i/4}, 2^{1/6}e^{\pm 5\pi i/12}, 2^{1/6}e^{\pm 11\pi i/12}$. These are plotted in the following diagram – notice that the solutions are in complex conjugate pairs:

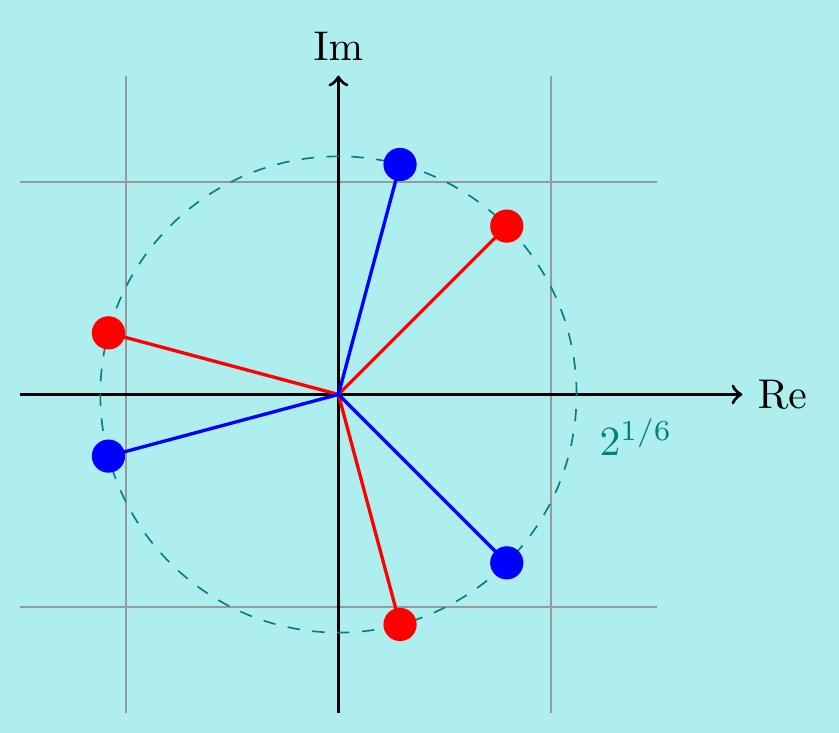
In fact, for any polynomial $p(z)$ with real coefficients, the roots are either real or occur in complex conjugate pairs. We already know this for quadratic equations, but you can show using the properties of complex conjugates that, if $p(z)=0$, then $p\left(\overline{z}\right)=0$ as well.

Another technique we can use to solve polynomial equations is factorisation.

Example. $\,$ Finding all solutions to $z^3=1$ is equivalent to factorising \[z^3-1 = (z-z_1)(z-z_2)(z-z_3),\] and the roots are then $z_1$, $z_2$, $z_3$. It’s easily seen that $z_1=1$ is a solution, so $(z-1)$ must be a factor and \[ z^3 - 1 = (z-1)(az^2 + bz + c) \] for some coefficients $a,b,c$. Multiplying out gives \[ z^3 - 1 = az^3 + (b-a)z^2 + (c-b)z - c. \] Equating coefficients on the left and right gives $a=b=c=1$, so \[ z^3 - 1 = (z-1)(z^2 + z + 1). \] The solutions to $z^2 + z + 1=0$ give the other two roots \[ z_2,z_3 = \frac{-1\pm\sqrt{-3}}{2} = -\frac12 \pm i\frac{\sqrt{3}}{2} = e^{\pm 2\pi i/3}. \]

2.6 Complex Logarithms

Suppose we want to solve the equation \[ e^z = 1. \] For real numbers, we know there is one solution $z=\ln1 = 0$, but for complex numbers there are more solutions. Writing $z=x+iy$ and $1=e^{2n\pi i}$ for any $n\in\mathbb{Z}$, we get \[ e^xe^{iy} = e^{2n\pi i} \quad\text{for any $n\in\mathbb{Z}$}. \] Equating modulus and argument shows that $e^x=1$ (meaning $x=0$) and $y=2n\pi$. In other words, \[ e^z = 1 \quad \iff \quad z = 2n\pi i \quad\text{for any $n\in\mathbb{Z}$}. \]

Now suppose we wish to solve a more general equation for any $w\in\mathbb{C}$ \[ e^z = w. \] Writing $w=se^{i\phi} = e^{\ln s + i\phi}$, we have \[\begin{align*} e^z = e^{\ln s + i\phi} &\quad\iff\quad e^{z - \ln s - i\phi} = 1 \\ &\quad\iff\quad z-\ln s - i\phi = 2n\pi i \quad\text{for $n\in\mathbb{Z}$}. \end{align*}\] So we have infinitely many solutions \[\begin{align*} z &= \ln s + i\phi + 2n\pi i \quad\text{for $n\in\mathbb{Z}$}\\ &= \ln|w| + i\arg w. \end{align*}\] This $z$ is what we mean by the logarithm of the complex number $w$. Notice that it is again multi-valued since $\arg(w)$ takes infinitely many values.

Recall that the principal argument $\operatorname{Arg}(w)$ is the particular angle such that $-\pi<\operatorname{Arg}(w)\leq\pi$. Similarly we define the principle value of the logarithm to be \[ \operatorname{Ln}(w) = \ln|w| + i\operatorname{Arg}(w). \]

Example. $\,$ Solve $e^z=-1$ and hence find $\operatorname{Ln}(-1)$.

We have \[ z = \ln|-1| + i\arg(-1) = 0 + \pi i + 2n\pi i = (2n+1)\pi i \] so taking the principal value gives \[\operatorname{Ln}(-1)=i\pi.\] Notice this is just a restatement of the fact $e^{\pi i}=-1$.

2.7 De Moivre’s Theorem

If we replace $\theta$ in Euler’s formula \[ e^{i\theta} = \cos\theta + i\sin\theta \] with $n\theta$ for integer $n$, then \[ e^{in\theta} = \cos(n\theta) + i\sin(n\theta). \] But clearly $e^{in\theta}=\left(e^{i\theta}\right)^n$ and so we get de Moivre’s Theorem: \[ \cos(n\theta) + i\sin(n\theta) = (\cos\theta + i\sin\theta)^n. \]

We can use this to easily prove various trigonometric identities for real $\theta$.

Example. $\,$ Express $\cos(3\theta)$ and $\sin(3\theta)$ in terms of $\cos\theta$ and $\sin\theta$.

From de Moivre’s Theorem, \[\begin{align*} \cos(3\theta)+i\sin(3\theta)&=\left(\cos\theta+i\sin\theta\right)^3, \\ &=\cos^3\theta+3\cos^2\theta(i\sin\theta)+3\cos\theta(i\sin\theta)^2+(i\sin\theta)^3, \\ &=\left(\cos^3\theta-3\cos\theta\sin^2\theta\right) +i\left(3\cos^2\theta\sin\theta-\sin^3\theta\right). \end{align*}\] Now equating real and imaginary parts gives \[\begin{align*} \cos(3\theta)&=\cos^3\theta-3\cos\theta\sin^2\theta, \\ \sin(3\theta)&=3\cos^2\theta\sin\theta-\sin^3\theta. \end{align*}\] We could go a little further, using $\cos^2\theta+\sin^2\theta=1$ to see \[\begin{align*} \cos(3\theta)&=\cos^3\theta-3\cos\theta(1-\cos^2\theta)=4\cos^3\theta-3\cos\theta, \\ \sin(3\theta)&=3(1-\sin^2\theta)\sin\theta-\sin^3\theta=3\sin\theta-4\sin^3\theta. \end{align*}\]

2.8 Trigonometric Functions

De Moivre’s Theorem with $n=\pm1$ gives the two equations \[\begin{align*} e^{i\theta} &= \cos\theta + i\sin\theta,\\ e^{-i\theta} &= \cos\theta - i\sin\theta, \end{align*}\] which may be solved simultaneously to give the important expressions \[ \cos\theta = \frac{e^{i\theta} + e^{-i\theta}}{2} \quad\text{and}\quad \sin\theta = \frac{e^{i\theta} - e^{-i\theta}}{2i}. \]

Notice the similarity to what we learnt about hyperbolic functions in the Induction week Warm-up. If we leave out the $i$’s in the above formulae, we get \[ \cosh\theta = \frac{e^\theta + e^{-\theta}}{2}\quad \text{and}\quad \sinh\theta = \frac{e^\theta-e^{-\theta}}{2}, \] and in fact we can relate the trigonometric and hyperbolic functions: \[\cos\theta=\cosh(i\theta) \quad\text{and}\quad \sin\theta=\frac{\sinh(i\theta)}{i}. \]

We can use the exponential expressions for $\cos\theta$ and $\sin\theta$ to easily derive trigonometric identities.

Example. $\,$ Show that \[ \cos^2\theta=\frac{1 + \cos(2\theta)}{2} \quad\text{and}\quad \sin^2\theta = \frac{1-\cos(2\theta)}{2}. \]

Just substitute the formulas in and simplify: \[\begin{align*} \cos^2\theta=\left(\frac{e^{i\theta}+e^{-i\theta}}{2}\right)^2 &=\frac{e^{2i\theta}+2+e^{-2i\theta}}{4} \\ &=\frac12+\frac12\left(\frac{e^{2i\theta}+e^{-2i\theta}}{2}\right)=\frac{1+\cos(2\theta)}{2}. \end{align*}\] Similarly, \[\begin{align*} \sin^2\theta=\left(\frac{e^{i\theta}-e^{-i\theta}}{2i}\right)^2 &=\frac{e^{2i\theta}-2+e^{-2i\theta}}{-4} \\ &=\frac12-\frac12\left(\frac{e^{2i\theta}+e^{-2i\theta}}{2}\right)=\frac{1-\cos(2\theta)}{2}. \end{align*}\]

The exponential expressions for $\cos\theta$ and $\sin\theta$ can also help with calculus of trigonometric functions.

Example. $\,$ Find $\displaystyle\frac{d}{dx}\cos x$ directly from the exponential formula.

Differentiating gives \[ \frac{d}{dx}\cos x = \frac{ie^{ix} - ie^{-ix}}{2} = i^2\left(\frac{e^{ix} - e^{-ix}}{2i} \right) = -\sin x. \]

Example. $\,$ Find $\color{maroon}{\displaystyle\int e^{ax}\cos(bx)\,dx}$ and $\color{teal}{\displaystyle\int e^{ax}\sin(bx)\,dx}$, where $a,b\in\mathbb{R}$ are not both zero.

We could do each of these using integration by parts twice. However, notice that \[ e^{ax}\cos(bx) + ie^{ax}\sin(bx) = e^{ax}e^{ibx} = e^{(a+ib)x}, \] so \[\begin{align*} \color{maroon}{\int e^{ax}\cos(bx)\,dx} &+ i\color{teal}{ \int e^{ax}\sin(bx)\,dx} = \int e^{(a+ib)x}\,dx \\ &= \frac{1}{a+ib}e^{(a+ib)x} + C \\ &= \left(\frac{a-ib}{a^2+b^2}\right)e^{ax}\big(\cos(bx) + i\sin(bx)\big) \\ &=\color{maroon}{ \frac{e^{ax}\left(a\cos(bx) + b\sin(bx)\right)}{a^2 + b^2}} \\ &\qquad\qquad +i\color{teal}{\frac{e^{ax}\left(a\sin(bx) - b\cos(bx)\right)}{a^2 + b^2}} + C. \end{align*}\] Equating real and imaginary parts gives us both integrals at once.

We can use the exponential expressions to define $\cos z$ and $\sin z$ for arbitrary complex numbers: \[ \cos z = \frac{e^{iz} + e^{-iz}}{2} \quad\text{and}\quad \sin z = \frac{e^{iz} - e^{-iz}}{2i}. \]

This has a number of surprising consequences. For instance, $\sin{z}$ can take values which are not just real numbers between $-1$ and $1$.

Example. $\,$ Find all complex numbers $z$ satisfying $\sin z = 2$.

We want to find all $z$ so that \[ \frac{e^{iz} + e^{-iz}}{2i} = 2 \quad \iff \quad e^{2iz} - 4ie^{iz} - 1 = 0. \] Writing $w=e^{iz}$, this is a quadratic in $w$, which we know how to solve: \[ w^2 - 4iw - 1 = 0 \quad\iff\quad w = \frac{4i\pm\sqrt{(4i)^2 + 4}}{2} = i(2\pm\sqrt{3}). \] Now we need to solve $e^{iz}=i(2\pm\sqrt{3}) = (2\pm\sqrt{3})e^{\pi i/2 + 2n\pi i}$ for $n\in\mathbb{Z}$.

Writing $z=x+iy$, we have \[\begin{align*} &e^{i(x+iy)} = e^{-y}e^{ix} = (2\pm\sqrt{3})e^{\pi i/2 + 2n\pi i},\\ &\iff\quad \begin{cases} x \!\!\!&= \frac12\pi + 2n\pi,\\ y \!\!\!&= -\ln(2\pm\sqrt{3}), \end{cases}\\ &\iff\quad z = \frac12\pi + 2n\pi - i\ln(2\pm\sqrt{3}) \quad\text{for $n\in\mathbb{Z}$}. \end{align*}\] In the complex plane, these look like two rows of equally spaced points:

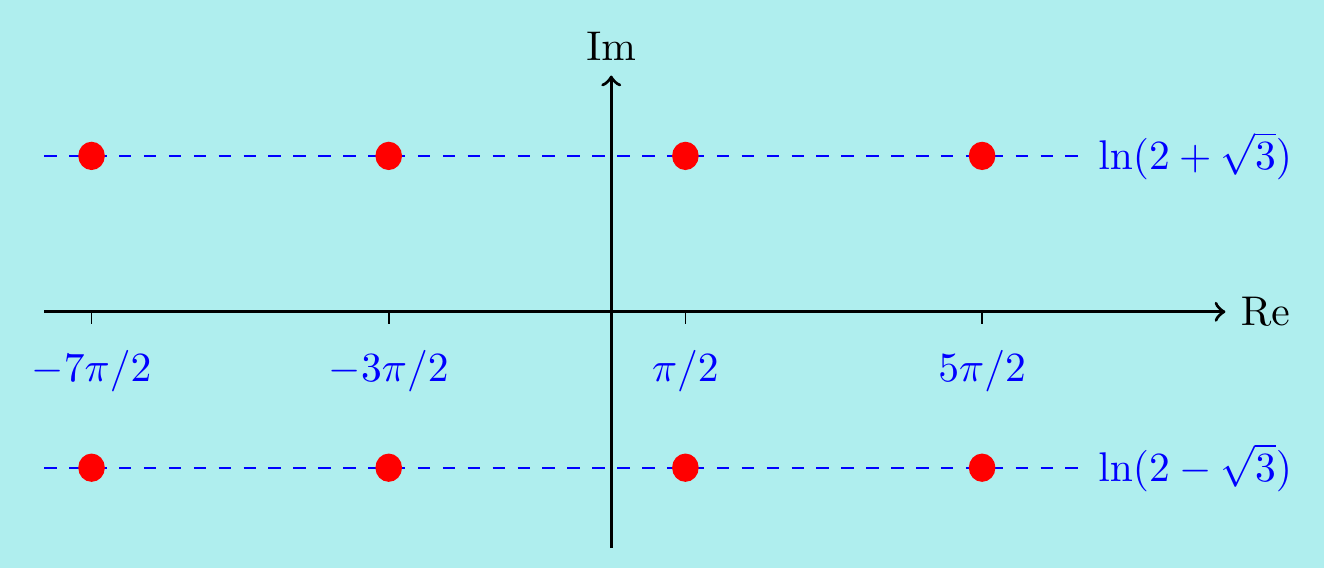
We could rewrite these solutions in a lightly nicer way as \[z = \frac12\pi + 2n\pi \pm i\ln(2+\sqrt{3})\] since $(2+\sqrt{3})(2-\sqrt{3}) = 1$ and so $\ln(2-\sqrt{3})=-\ln(2 + \sqrt{3})$.

In general, for complex $w$, you can show that \[ \arcsin w = -i\ln\Big(iw \pm \sqrt{1-w^2}\Big). \] Note that $\ln$ here is the complex logarithm so is multi-valued. This means that $\arcsin$ is also multivalued. We could define a principal value for it in the same way as we did for arguments and logarithms. Notice how similar this formula is to the formula for $\sinh^{-1}(x)$ from the Induction week Warm-up.

2.9 Application to Geometry

We’ve seen how complex numbers have a natural meaning in two-dimensional space. This connection can help us study problems in two-dimensional geometry.

Recall that, for a point $z$ in the complex plane, the modulus $|z|$ represents the distance from the origin and $\arg z$ represents the angle with the real (horizontal) axis. Also, arithmetic operations correspond to geometric ones. For instance:

Adding $w=u+iv$ translates by a distance $u$ horizontally and $v$ vertically.
Multiplying by a real number $s$ scales by a factor $s$.
Multiplying by $e^{i\phi}$ rotates anticlockwise by an angle $\phi$.

In particular, rotations in 2D are easier to handle compared to using normal coordinates. With complex numbers, it’s just multiplication! In fact, three dimensional rotations can be handled using a generalization of the complex numbers called quaternions, but these are beyond the scope of this course.

Example. $\,$ An equilateral triangle has centre at $(3,3)$ and a vertex at $(4,5)$. Find the coordinates of the other vertices and the length of the sides.

In the complex plane, the centre is at $z_0=3+3i$ and one vertex is at $z_1 = 4+5i$. We want to find the other two vertices $z_2$, $z_3$ as shown in the left-hand picture:

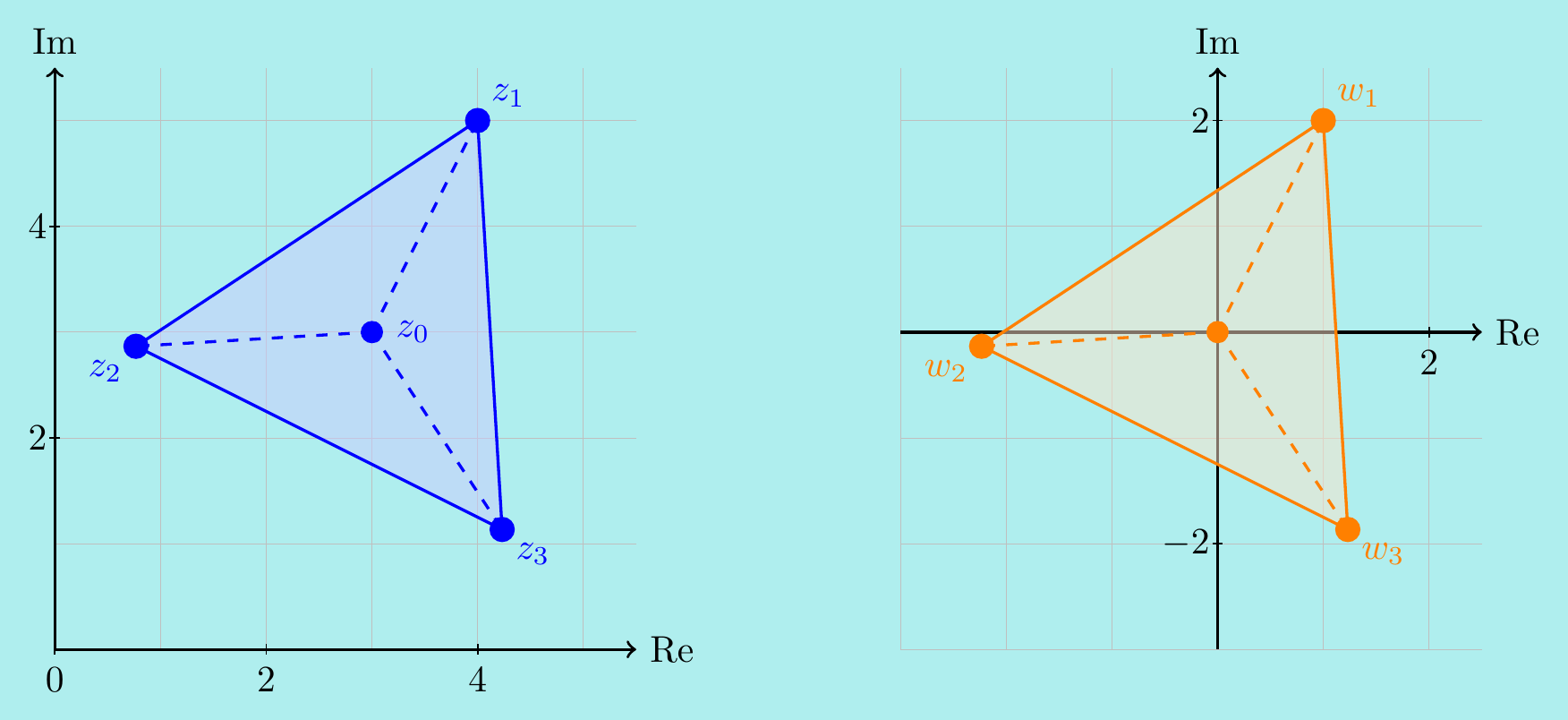
We can find these by rotating $z_1$ around $z_0$ through angles $\pm2\pi/3$ respectively. Rotating around the origin would be easier, since then we just multiply by $e^{\pm 2\pi i/3}$. To rotate around $z_0$, we first translate the picture so that $z_0$ moves to the origin. So set $w_1 = z_1-z_0$, $w_2=z_2-z_0$ and $w_3=z_3-z_0$. Now we have the right hand picture, where \[\begin{align*} w_2 = e^{2\pi i/3}w_1 \quad &\implies \quad z_2 - z_0 = e^{2\pi i/3}(z_1-z_0),\\ w_3 = e^{-2\pi i/3}w_1 \quad &\implies \quad z_3 - z_0 = e^{-2\pi i/3}(z_1-z_0). \end{align*}\] Using $e^{\pm 2\pi i/3} =\cos\left(\pm\frac23\pi\right) + i\sin\left(\pm\frac23\pi\right) =-\frac12 \pm i\frac12\sqrt{3}$, we get \[\begin{align*} z_2 &= z_0 + e^{2\pi i/3}(z_1-z_0) = 3 + 3i + \left(-\frac12 + i\frac{\sqrt{3}}{2} \right)(1+2i) \\ &\qquad=\left(\frac52 - \sqrt{3}\right) + i\left(2+\frac{\sqrt{3}}{2}\right),\\ z_3 &= z_0 + e^{-2\pi i/3}(z_1-z_0) = 3 + 3i + \left(-\frac12 - i\frac{\sqrt{3}}{2} \right)(1+2i) \\ &\qquad= \left(\frac52 + \sqrt{3}\right) + i\left(2-\frac{\sqrt{3}}{2}\right). \end{align*}\] The real and imaginary parts of these give the required coordinates. Also, the length of the sides is \[\begin{align*} |z_1-z_2| &= \left|4 + 5i - \left(\frac52 - \sqrt{3}\right) - i\left(2 + \frac{\sqrt{3}}{2}\right)\right|\\ &= \left|\left(\frac32 + \sqrt{3}\right) + i\left(3 - \frac{\sqrt{3}}{2}\right)\right|\\ &= \sqrt{\left(\frac32+\sqrt{3}\right)^2 + \left(3 - \frac{\sqrt{3}}{2}\right)^2} = \sqrt{15}. \end{align*}\]

Here’s a similar, general fact you could try to prove as an exercise: suppose a triangle has vertices at $z_1$, $z_2$ and $z_3$ (taken in anticlockwise order). Show that it is equilateral if and only if \[z_1+\omega z_2+\omega^2z_3=0\qquad\text{where $\omega=e^{2\pi i/3}$}.\]

Hint: notice it’s equilateral if and only if $z_3-z_2=\omega(z_2-z_1)$ and use the fact that $\omega^2=-\omega-1$.

Complex numbers also give a convenient way to define various curves and regions. Let’s look at a few examples.

Example. $\,$ Given a complex number $w$ and a real number $R>0$, sketch the points satisfying $|z-w| = R$.

Notice that $|z-w|$ is the distance between $z$ and $w$. We are thus looking at all points $z$ which are distance $R$ away from $w$. It’s just a circle!

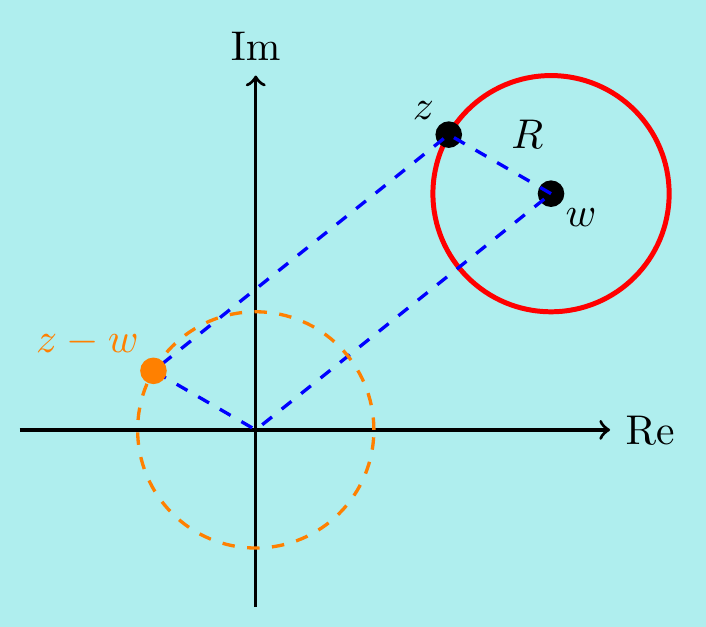
You can easily check this algebraically: if $z=x+iy$ and $w=u+iv$ then \[ |z - w|^2 = (x-u)^2 + (y-v)^2 = R^2. \]

Example. $\,$ Sketch the set of points $z$ satisfying $\;|z-2| = |z-3i|$.

The equation says that $z$ is equidistant from the point $2$ and the point $3i$, so it must be the perpendicular bisector line:

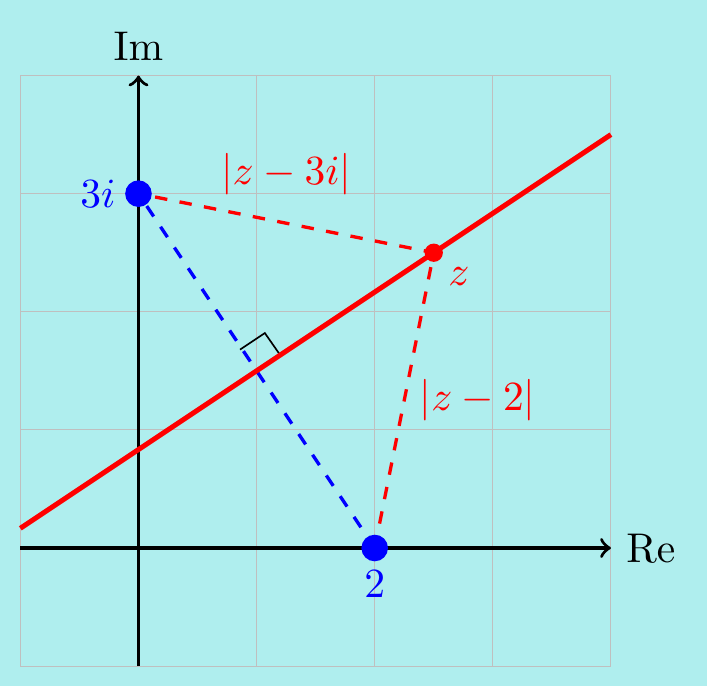
To see this algebraically, let $z=x+iy$ so \[\begin{align*} |z-2|^2 = |z-3i|^2 \quad &\implies \quad (x-2)^2 + y^2 = x^2 + (y-3)^2,\\ &\implies \quad -4x + 4 = -6y + 9,\\ &\implies \quad y = \frac{4x+5}{6}. \end{align*}\]

Example. $\,$ Sketch the set of points $z$ satisfying $\;\displaystyle\frac{\pi}{6} \leq \arg(z-1-i)\leq\frac{\pi}{3}$.

This says that the angle between the line from $z$ to $1+i$ and the real axis is between $\pi/6$ and $\pi/3$. That make the region a wedge shape between two lines.

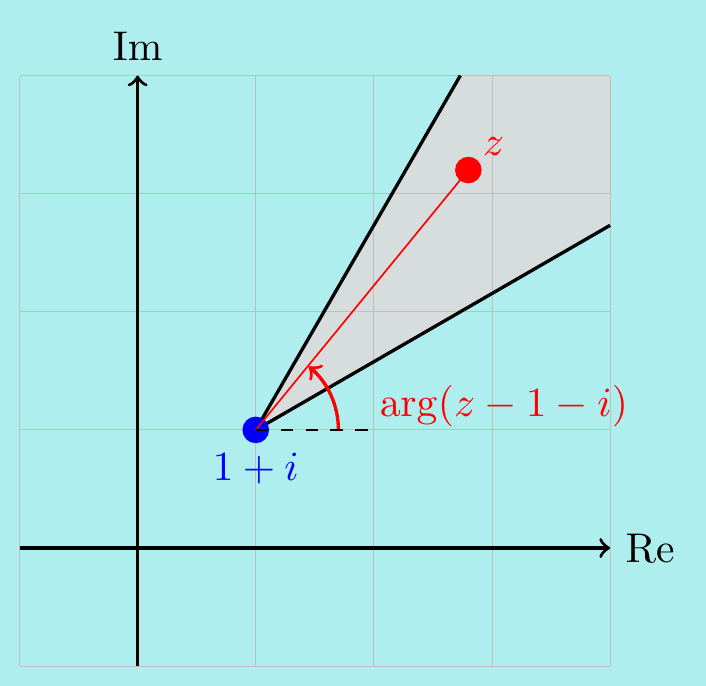
Algebraically, if $z=x+iy$ then \[ \frac{1}{\sqrt{3}}\leq\tan\arg(z-1-i) = \frac{y-1}{x-1}\leq \sqrt{3}, \] so \[ \frac{x-1}{\sqrt{3}}+1\leq y \leq \sqrt{3}(x-1) + 1. \] Hence $z$ lies in the region between the two lines and with $x\geq 1$.

Complex numbers also give a particularly elegant proof of the triangle inequality: this says that if a triangle with side lengths $a$, $b$, $c$, then $a\leq b+c$. The equivalent statement using complex numbers says that for any two complex numbers $z$, $w$ we have \[ |z + w| \leq |z| + |w|. \]

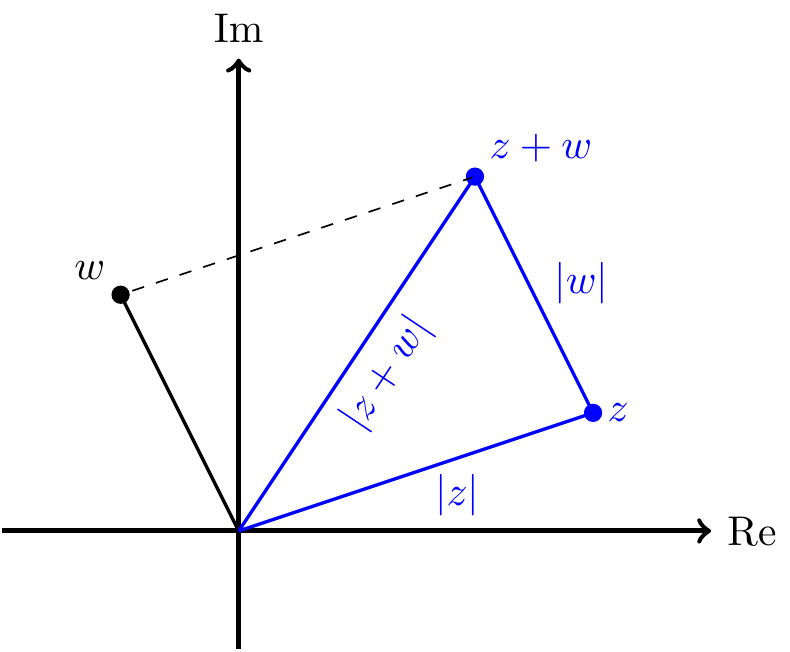
To prove this, remember that $|z|^2 = z\overline{z}$, $|w|^2=w\overline{w}$, and \[\begin{align*} |z+w|^2 &= (z+w)\overline{(z + w)}\\ &= (z+w)(\overline{z} + \overline{w})\\ &= z\overline{z} + z\overline{w} + \overline{z}w + w\overline{w}\\ &= |z|^2 + |w|^2 + z\overline{w} + \overline{z}w. \end{align*}\] Now let $z\overline{w}=a+ib$ for real numbers $a$ and $b$. Then \[\begin{align*} z\overline{w} + \overline{z}w &= z\overline{w} + \overline{z\overline{w}} \\ &= 2\operatorname{Re}(z\overline{w}) \\ &=2a \leq 2\sqrt{a^2 + 0^2} \\ &\leq 2\sqrt{a^2 + b^2} \\ &= 2|z\overline{w}|. \end{align*}\] Combining, we see that \[\begin{align*} |z + w|^2 &\leq |z|^2 + |w|^2 + 2|z\overline{w}| \\ &= |z|^2 + |w|^2 + 2|z||w| \\ &= (|z| + |w|)^2 \end{align*}\] and taking square roots gives the required inequality.

2.10 Application to AC Circuits

Complex numbers are very good for analysing things that vary in waves. In particular, they help us to analyse AC (alternating current) electrical circuits.

For the purposes of this module, we don’t expect you to know anything about AC circuits. However, below we will set up the background to create some formulas involving complex numbers. You would then be expected to know how to manipulate these formulas if they were given to you.

In an AC circuit, the current varies sinusoidally, so in particular, could be of the form \[ I = I_0\cos(\omega t) \] for (real) constants $I_0$ and $\omega$. In particular, $I_0$ is the amplitude and $\omega/(2\pi)$ is the frequency. In other words, the current completes a whole sinusoidal cycle when $t$ increases by $2\pi/\omega$.

An RLC circuit consists of some combination of three types of component:

$\;\;\;$ The voltage across a resistor is proportional to the current (this is Ohm’s Law) \[ V_R = IR = I_0R\cos(\omega t). \]

$\;\;\;$ The voltage across a capacitor accumulates at a rate proportional to the current: \[ V_C = \frac{1}{C}\int I\,dt = \frac{I_0}{\omega C}\sin(\omega t). \]

$\;\;\;$ The voltage across an inductor is proportional to the rate of change of current: \[ V_L = L\frac{dI}{dt} = -\omega LI_0\sin(\omega t). \]

So the voltage across a resistor $V_R$ oscillates in sync with $I$ but $V_C$ and $V_L$ are out of sync with I, with phase differences $\pm\pi/(2\omega)$.

Complex numbers allow us to handle these voltages across all three components in a uniform way. The trick is to think of the current $I$ as the real part of a complex current \[\widehat{I} = I_0e^{i\omega t}.\]

We now express everything as the real parts of complex quantities, using \[e^{i\omega t}=\cos(\omega t)+i\sin(\omega t).\] Notice that multiplying by $\pm i=e^{\pm \frac{\pi}{2}i}$ allows us to switch between cosines and sines:

$\;\;\;\,\cos(\omega t)$ is the real part of $e^{i\omega t}$,
$\;\;\;\,\sin(\omega t)=\cos\left(\omega t-\frac{\pi}{2}\right)$ is the real part of $e^{i(\omega t-\frac{\pi}{2})}=-ie^{i\omega t}$,
$-\sin(\omega t)=\cos\left(\omega t+\frac{\pi}{2}\right)$ is the real part of $e^{i(\omega t+\frac{\pi}{2})}=ie^{i\omega t}$.

The voltages across our components are hence the real parts of multiples of $\widehat{I}$:

$V_R$ is the real part of $\widehat{I}R$.
$V_C$ is the real part of $\displaystyle\widehat{I}\left(\frac{-i}{\omega C}\right)$.
$V_L$ is the real part of $\widehat{I}(i\omega L)$.

Each of these is the real part of a complex voltage $\;\widehat{V}=\widehat{I}Z,\;$ where $Z$ is called the complex impedance: \[ Z_R = R, \qquad Z_C=\frac{-i}{\omega C}, \qquad Z_L=i\omega L. \]

In a circuit with more than one component, the rules for adding impedances are the same as for adding resistances in a DC circuit. So in a circuit with impedances $Z_1,Z_2,\ldots,Z_n$ in series, the total impedance is \[ Z = Z_1 + Z_2 + \ldots + Z_n. \] For a circuit with impedances $Z_1,Z_2,\ldots,Z_n$ in parallel, the total impedance satisfies \[ \frac{1}{Z} = \frac{1}{Z_1} + \frac{1}{Z_2} + \ldots + \frac{1}{Z_n}. \]

Example. $\,$ For the following “series RLC circuit” with current $I=I_0\cos(\omega t)$, find the value of $\omega$ which minimises the magnitude of the total impedance. Also, find the phase difference between the current and voltage in terms of $\omega$.

The total impedance is \[ Z = Z_R + Z_L + Z_C = R + i\omega L - \frac{i}{\omega C} = R + i\left(\omega L - \frac{1}{\omega C}\right). \] This has modulus \[ |Z| = \sqrt{R^2 + \left(\omega L - \frac{1}{\omega C}\right)^2}, \] and since the two terms inside the square root are positive, we clearly want to find $\omega$ so that the second term vanishes: \[ \omega L - \frac{1}{\omega C} = 0 \quad \implies \quad \omega = \frac{1}{\sqrt{LC}}. \] Furthermore, since the (complex) voltage and (complex) current are related by $\widehat{V}=\widehat{I}Z$, the phase difference is $\phi=\arg{Z}=\arg(\widehat{V})-\arg(\widehat{I})$. With $Z$ as above, this means \[\tan\phi=\frac{1}{R}\left(\omega L-\frac{1}{\omega C}\right).\]

Since the impedance is minimal for this value of $\omega$, the circuit is ``tuned’’ to allow this particular frequency $\omega/(2\pi)$ through most easily. It is called the resonant frequency of the circuit Also, $\phi$ is called the phase of the circuit - the voltage is a sinusoidal wave tracking the (sinusoidal) current with a phase-lag of $\phi$.

Here is a more complicated example.

Example. $\,$ For the following “parallel RC circuit”, show that as $\omega$ varies from $0$ to $\infty$, the total complex impedance traces out a semi-circle centred at $z=\frac12R$ in the complex plane. Find its radius.

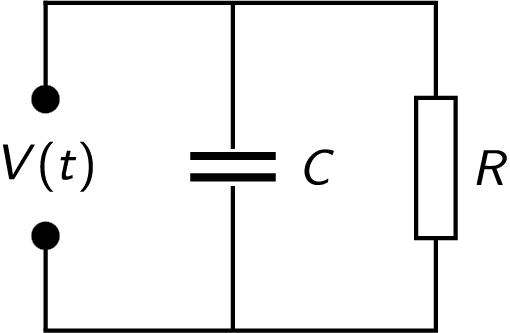
The total impedance $Z$ satisfies \[ \frac{1}{Z} = \frac{1}{R} - \frac{\omega C}{i} \quad\implies\quad Z = \frac{R}{1 + iR\omega C}. \] To show that it traces out a semi-circle, we compute the real and imaginary parts: \[\begin{align*} Z = \frac{R(1 - iR\omega C)}{1^2 + (R\omega C)^2} = \frac{R}{1 + (R\omega C)^2} - i\frac{R^2\omega C}{1 + (R\omega C)^2}. \end{align*}\] If $Z=X+iY$ lies on the given semicircle, then $(X - \frac12R)^2 + Y^2$ should be equal to a constant independent of $\omega$. With some complicated (but mindless) algebra, we find this constant is just $R^2/4$: \[\begin{align*} \left(X - \frac{R}{2}\right)^2 + Y^2 &= \left(\frac{R}{1+(R\omega C)^2} - \frac{R}{2}\right)^2 + \left(\frac{R^2\omega C}{1 + (R\omega C)^2} \right)^2,\\ &= \left(\frac{2R - R(1+(R\omega C)^2)}{2(1+(R\omega C)^2)}\right)^2 + \left(\frac{2R^2\omega C}{2(1 + (R\omega C)^2)} \right)^2,\\ &= \frac{R^2}{4}\left[\left(\frac{1-(R\omega C)^2}{1+(R\omega C)^2}\right)^2 + \left(\frac{2R\omega C}{1 + (R\omega C)^2} \right)^2\right],\\ &= \frac{R^2}{4}\left[\frac{1-2(R\omega C)^2 + (R\omega C)^4 + 4(R\omega C)^2}{(1+(R\omega C)^2)^2}\right],\\ &= \frac{R^2}{4}\left[\frac{(1+(R\omega C)^2)^2}{(1+(R\omega C)^2)^2}\right],\\ &= \frac{R^2}{4}. \end{align*}\] So $Z$ lies on a circle radius $\dfrac12R$ and centred at $\left(\dfrac12R,0\right)$.

In fact, $Z$ lies on the semi-circle below the real axis because \[Y=\frac{-R^2\omega C}{1 + (R\omega C)^2}\leq 0\quad\text{for all $\omega\geq 0$.}\]

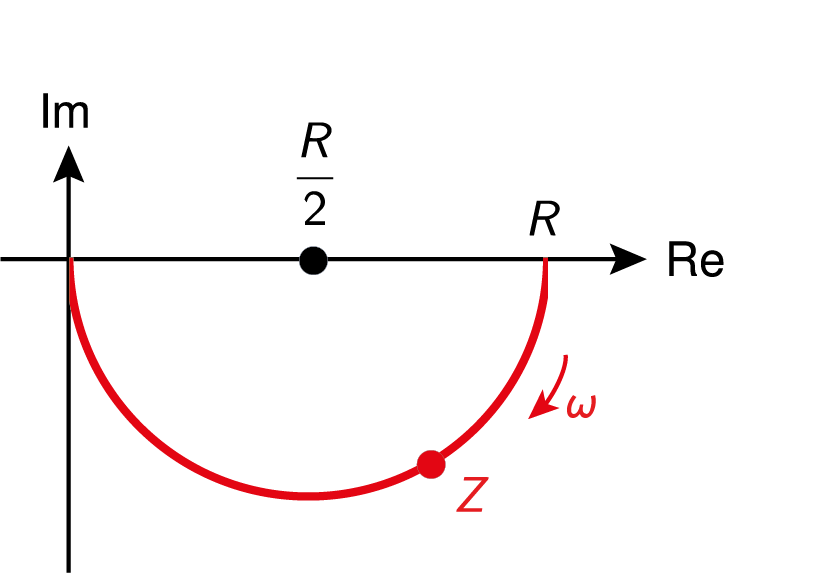
Notice that as $\omega\to 0$, the complex impedance $Z$ reduces to $R$, corresponding to a constant direct current (DC) through the resistor. As $\omega\to\infty$ we have $Z\to 0$ so high frequencies pass almost unimpeded.

A diagram showing complex impedance as a function of $\omega$ like this is sometimes called a Nyquist plot.