In this practical we use R to investigate the conjugate Bayesian analysis for Poisson data. We will also investigate using the effects of the prior distribution on the posterior, and the situation where our sample size grows large.

Download the R Script - right click, and Save As

You will need the following skills from previous practicals:
- Creating vectors with seq
- Drawing functions with plot, and with lines
- Using additional graphical parameters to customise plots with colour (col), line type (lty), axis range (xlim and ylim) etc
- Adding simple straight lines to plots with abline
- Writing your own functions with function
- Using sapply to evaluate a function on every element of a vector
New(ish) R techniques:
- Using R’s built-in functions to evaluate a standard pdf, e.g. dgamma and dnorm
- Using the quantile functions, e.g. qgamma, to produce exact credible intervals using standard distributions

1 The Data

Our dataset concerns the number of volcanoes that erupted each year from 2000 to 2018, taken from here. The data are given in the table below, where each volcanic eruption is counted in the year that the eruption started. Volcanic eruptions are split into groups depending on the severity of the eruption, as measured on the logarithmically-scaled Volcanic Explosivity Index (VEI). For example, the 2010 eruption of Eyjafjallajökull in Iceland had a VEI of 4, whereas the eruption of Krakatoa in 1883 was VEI6.

The eruptions are classified as Small (VEI$\leq 2$), Medium (VEI $=3$), and Large (VEI $\geq 4$).

Year	2000	2001	2002	2003	2004	2005	2006	2007	2008	2009
Small	30	25	30	32	29	29	34	29	25	28
Medium	6	6	5	5	8	4	3	3	7	2
Large	0	0	0	2	1	1	1	3	2	1

Year	2010	2011	2012	2013	2014	2015	2016	2017	2018
Small	39	30	40	40	41	26	37	30	34
Medium	6	6	4	7	7	5	4	6	4
Large	3	0	1	0	1	0	2	0	1

Run the R code below to input the data, and create a new data frame called volcano, with columns Year, Small, Medium, and Large.
plot the number of Small eruptions against the year using a vertical axis range (ylim) of $[0,50]$. Add lines of different colours to the same plot for the other two groups of eruptions. Do you see any apparent relationship between time and number of eruptions?
Also plot the histogram of the number of Medium eruptions - does it look like it could follow a Poisson distribution? How else could you quickly assess this?

volcano <- data.frame(Year = 2000:2018, 
           Small = c(30, 25, 30, 32, 29, 29, 34, 29, 25, 28, 39, 30, 
                     40, 40, 41, 26, 37, 30, 34), 
           Medium = c(6, 6, 5, 5, 8, 4, 3, 3, 7, 2, 6, 6, 4, 7, 7, 
                      5, 4, 6, 4),
           Large = c(0, 0, 0, 2, 1, 1, 1, 3, 2, 1, 3, 0, 1, 0, 1, 
                     0, 2, 0, 1))

2 Conjugate analysis with the Gamma-Poisson model

2.1 The Theory

A Poisson distribution is often used to model the counts of random events occurring within a fixed period of time at some rate $\lambda$. For such a random variable $X$ where $X\sim\text{Po}(\lambda)$ , a Bayesian analysis will require a prior distribution for the unknown Poisson parameter $\lambda$. We have seen/will see (Lecture 16) that the Gamma distribution provides a conjugate prior for this particular problem. Therefore, if our data $X_1,\dots,X_n$ are $\text{Po}(\lambda)$, and our prior distribution for $\lambda$ is $\text{Ga}(a,b)$. Then the posterior distribution for $\lambda ~|~ X_1,\dots,X_n$ is given by: \[ \lambda ~|~ X_1,\dots,X_n \sim \text{Ga}(a+T, b+n), \] where $T=\sum_{i=1}^n X_i= n\overline{X}$.

2.2 The prior

First, let’s use the Gamma distribution to identify an appropriate prior for our Poisson count data.

R provides built-in functions to evaluate the PDF of standard distributions. The density function for a Gamma distribution $\text{Ga}(a,b)$ is used as follows

dgamma(x, shape=a, rate=b)

where x is the point (or vector of points) where we want to evaluate the PDF, and a and b are the usual Gamma parameter values.

Create a vector containing a sequence of 500 equally-space values over the interval $[0,10]$. Call this lambdavals.
Evaluate the $\text{Ga}(1,1)$ pdf at each of the values of $\lambda$ in lambdavals using the gamma PDF dgamma. Make a plot of the pdf against $\lambda$ as a solid black line.

An expert vulcanologist believes that the unknown rate of Medium eruptions, $\lambda$, is such that a range of $[1,6]$ would be plausible.

Interpret the expert’s given interval as corresponding to a statement of $\text{mean}(\lambda) \pm 2\text{sd}(\lambda)$. Hence, find the mean and variance of the prior.
Equate the prior mean and variance to the theoretical values for the expectation ($a/b$) and variance ($a/b^2$) of a Gamma pdf, and hence find the appropriate values of its parameters $a$ and $b$.
Evaluate the expert’s prior pdf for $\lambda$ at each of lambdavals, and save it as cnjPrior.
Normalise cnjPrior so that its values sum to 1.
Produce a fresh plot of the expert’s prior pdf for $\lambda$ as a solid red curve. Ensure your vertical axis covers $[0,0.02]$.
Add a vertical red and dashed line (abline using the v argument) at the location of the prior expectation for $\lambda$.

In addition to built-in functions for PDFs of standard distributions, R also provides the quantile function for a pdf. The quantile function evaluates the inverse of the cumulative distribution function, $F_X^{-1}(u)$. Given a probability value $u\in[0,1]$, the quantile function returns the value $x$ of $X$ for which $P[X\leq x]=u$, and so the quantile functions are particularly useful for finding critical values of distributions and for finding exact credible intervals.

The quantile function for a Gamma density $X\sim \text{Ga}(\alpha,\beta)$ is used as follows

qgamma(alpha, shape=a, rate=b)

where alpha is the lower tail probability (or vector of lower-tail probabilities) for which we want the corresponding value(s) of $X$, and a and b are the usual Gamma parameter values.

Use the qgamma function to find a 95% equal-tailed prior credible interval for $\lambda$ using the expert’s prior distribution above. Hint: find the values of $\lambda$ with lower and upper tail probabilities of $2.5\%$.
How does this compare to the expert’s original interval?

2.3 The likelihood

The next ingredient in the Bayesian calculation requires us to capture the information contained in the data via the likelihood. In a Bayesian context, the likelihood is the conditional distribution of the data $X_1,\dots, X_n$ given the parameter $\lambda.$

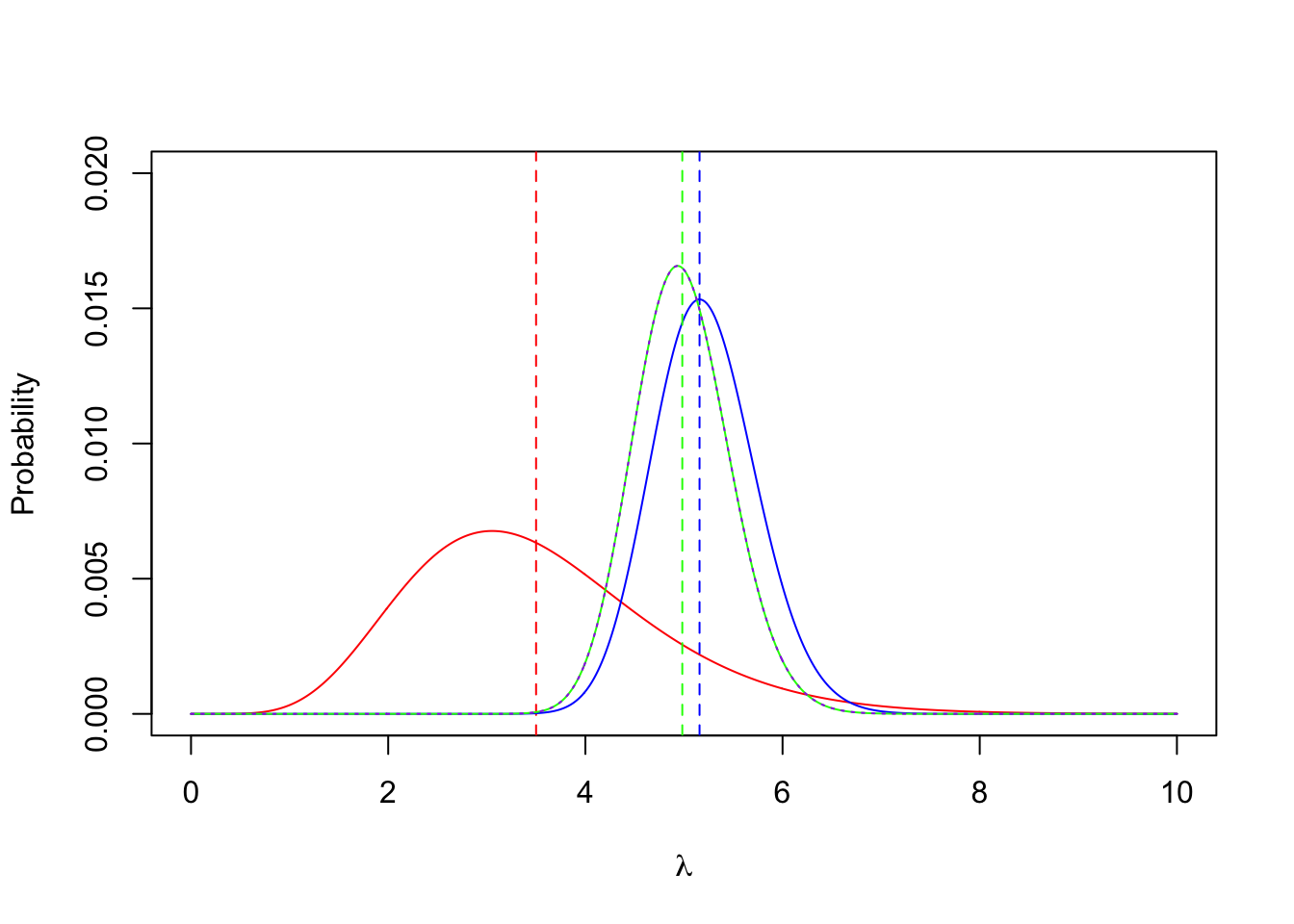
Let’s compute the likelihood given our data on Medium volcanic eruptions, and add it to the plot.

Write a function poisLike hat computes the Poisson likelihood for the sample of Medium volcano eruptions. Your function should:
- Take one argument lambda
- Compute the Poisson probability for each data point in volcano$Medium given the value of lambda. Hint: the dpois function evaluates Poisson probabilities for a vector of values x and parameter lambda.
- Combine the probabilities to find the likelihood of the sample, and return it.
Use sapply to evaluate the Poisson likelihood (poisLike) for each of the values of $\lambda$ in lambdavals. Save this as like.
Normalise like so that its values sum to $1$.
Add the likelihood to your plot of the prior distribution as a blue curve.
Add the maximum likelihood estimate of $\lambda$ as a vertical dashed blue line. Hint: You saw an expression for $\widehat{\lambda}$ in Term 1.

2.4 The posterior

As we’re using the conjugate Gamma prior with a Poisson likelihood, then our posterior distribution for $\lambda$ will also be a Gamma with parameter values as given in Section 2.1. Let’s verify that this is the case, and add the resulting density function to our plot.

Directly compute the posterior for $\lambda$ by Bayes theorem, and save these values as postDirect. Normalise the postDirect so that it sums to $1$. Hint: $\text{Posterior} \propto \text{Likelihood} \times \text{Prior}$.
Add the posterior to your plot as a solid green curve.
Now use conjugacy to evaluate the conjugate Gamma posterior distribution.
- First find the posterior values of $a$ and $b$, save these as aPost and bPost.
- Now use dgamma with the posterior parameter values to evaluate the posterior Gamma density at each of lambdavals. Save these values to postConjugate and normalise to sum to $1$.
Draw the conjugate posterior on your plot as a dashed purple curve.
What do you see? Do the results agree with each other? How has the prior changed?
Add the posterior mean as a vertical green line. What do you notice about the relationship between the posterior mean, the prior mean, and the maximum likelihood estimate?

Use the exact Gamma posterior to find a 95% posterior credible interval for $\lambda$.
Compare the posterior interval with the prior interval you found in Ex. 2.3. What has changed?

3 Exploring the effects of prior choice and sample size

3.1 Changing the prior parameters

To investigate how sensitive our results are to our choices for $a$ and $b$ in the prior Gamma distribution, we’re going to want to repeat our previous calculations for different values of the prior parameters. To make this easier, let’s wrap those calculations and plots in a new function that finds and draws the Gamma posterior for a given prior and data set:

Write a function called gammaPoisson which:
- Takes four arguments: the prior Gamma parameters a and b, and the summary statistics T and n.
- Computes the $\text{Ga}(a,b)$ prior and the $\text{Ga}(a+T,b+n)$ posterior over the sequence of values in lambdavals.
- Plots the (normalised) prior and posterior Gamma distributions as coloured curves on one plot.
- Adds the MLE as a dashed vertical line.
Check your function by evaluating it with the values of a,b,T, and n we used for the Medium volcano data above.

Investigate what happens as you change a and b.
How does the shape of the prior change? What impact does this have on the posterior distribution?
What happens for large values of a and b? How does this affect your results?

3.2 Updating beliefs with large samples

Theory in Lecture 18 will show that as the sample size grows large, the posterior distribution tends towards a Normal distribution and the posterior distribution becomes progressively less affected by the choice of prior distribution.

Let’s expand our data with the records of volcanic eruptions for the entire 20th century. As records are slightly incomplete, only the counts of Large eruptions over this period can be considered trustworthy. For the entire 100 years, a total of 64 Large (VEI$\geq 4$) eruptions were recorded

Combine the 20th century data with the data from 2000-2018 and compute new summary statistics for the Large volcanic eruptions from 1900-2018. Save these as Tbig and Nbig.
Use a prior of $\lambda\sim\text{Ga}(2,2)$, and plot the posterior given the combined data. What happens to the posterior?

The large sample of data is clearly very informative for $\lambda$, resulting in a posterior distribution that is concentrated over a small range of possible $\lambda$ values. Let’s refocus our plot on that sub-interval:

By modifying your Gamma-Poisson function, redraw the same plot to zoom in on the interval $\lambda\in[0.25,1.25]$. Hint: you’ll need to set the xlim argument to plot (or add it as an argument to your function).
What do you notice about the shape of the Gamma posterior distribution?

3.2.1 Theory: Limiting posterior distribution

From theory seen in Lecture 18, if we suppose that $X=(X_1,\dots,X_n)$ are an i.i.d. sample of size $n$ from a distribution with pdf $f(x~|~\theta)$ where $X_i \perp X_j ~|~ \theta$ and $f(x~|~\theta)$ is twice differentiable, then for $n$ ‘large enough’ the posterior distribution for $\theta ~|~ x$ is approximately \[ f(\theta ~|~ x) \approx \text{N}\left(\widehat{\theta}, \frac{1}{n\text{I}\left(\widehat{\theta}\right)}\right), \] where $\widehat{\theta}$ is the MLE of the parameter $\theta$, and $\text{I}(\widehat{\theta})$ is the observed Fisher information for a sample of size 1.

For a Poisson distribution, we have:

$\widehat{\lambda}=\frac{T}{n}$
$\text{I}(\lambda)=\frac{1}{\lambda}$.

Using the results above, compute the mean and variance of the limiting posterior distribution for the Large volcano eruption data.
Using dnorm, evaluate the approximating pdf for $\lambda$ over lambdavals. Normalise it, and add it to your plot using a thick dashed line.
Is the limiting normal distribution in agreement with the Gamma posterior? If it differs, how does it differ and to what extent?
Do the values of the Gamma prior parameters $a$ and $b$ affect the quality of the approximation?

Practical 2-5: Conjugate analysis of Poisson data