In this practical we use R to perform a Bayesian statistical analysis to learn about an underlying population quantity using a sample and a discrete prior distribution. We will also investigate using the conjugate Beta prior distribution, and the effects of a large sample on the posterior distribution.

  • You will need the following skills from previous practicals:
    • Basic R skills with arithmetic, functions, and vectors
    • Creating vectors with seq and rep
    • Drawing scatterplots with plot, and adding curves with lines
    • Using additional graphical parameters to customise plots with colour (col), line type (lty), etc
  • New(ish) R techniques:
    • Using variations of the plot function draw curves
    • Adjusting the plot axes with xlim and ylim, and adding a legend to the plot with legend
    • Writing your own functions with function
    • Using sapply to evaluate a function on every element of a vector

1 Bayesian Statistics

1.1 Bayesian Basics

The key idea behind Bayesian statistics is that we use probability to describe anything that’s uncertain, in particular both data, \(X\), and parameters, \(\theta\), are represented as random variables. Most Bayesian statistical questions about \(\theta\) can be answered by finding the conditional density (or probability): \[ f(\theta ~|~ x) = \frac{f(x~|~\theta)~f(\theta)}{f(x)} \]

where \(f(\theta)\) is our prior distribution for that describes our uncertainty in \(\theta\) before we see any data, \(f(x~|~\theta)\) is the likelihood of seeing the data given the model or parameter value \(\theta\), \(f(x)\) is the probability of seeing the data, and \(f(\theta~|~x)\) is the posterior distribution of the parameter \(\theta\) given what we have seen and learned from the data. In words, \[ \text{Posterior} = \frac{\text{Likelihood}\times\text{Prior}}{\text{Data probability}} \]

No matter how large the data set or complicated the distributions, all Bayesian approaches to statistical problems reduce to a calculation of this form.

1.2 Bayesian inference for a binomial proportion

In this practical, we will consider the hypothetical problem of assessing the proportion of people who vote for their current MP in an election, compared to those who vote for another candidate. Suppose we take a sample of \(n\) independent (and truthful) voters, and count the number, \(X\), who say they will vote for the MP. In this practical, our parameter of interest is the proportion of people, \(\theta\), in a group who will vote for the current MP.

Suppose we can only afford to make a small sample, and that 6 people from a sample of 10 support for the current MP. Our goal is to obtain the posterior distribution for the probability of support parameter, \(\theta\), given the sample, and investigate the effects of different prior distributions.

2 The Prior distribution

Let’s begin with a simple discrete distribution for \(\theta\). Suppose the proportion of supporters, \(\theta\), can only take one of the discrete values \(\theta_i\), where \[\theta_1 =\frac{0}{20}=0, \theta_2=\frac{1}{20}, \dots, \theta_{21}=\frac{20}{20}=1.\] Our Bayesian calculations will evaluate the prior probability, likelihood, and posterior probability for each of the possibile values of the parameter \(\theta\).

  • Create variables n and x and assign them the values of \(n\) and \(x\) for this problem.
  • Create a vector of the 21 possible values of \(\theta\), \(\theta_i\), and save it to thetavals. (Hint: use the seq function with the by argument to create a sequence of numbers with the same increment)

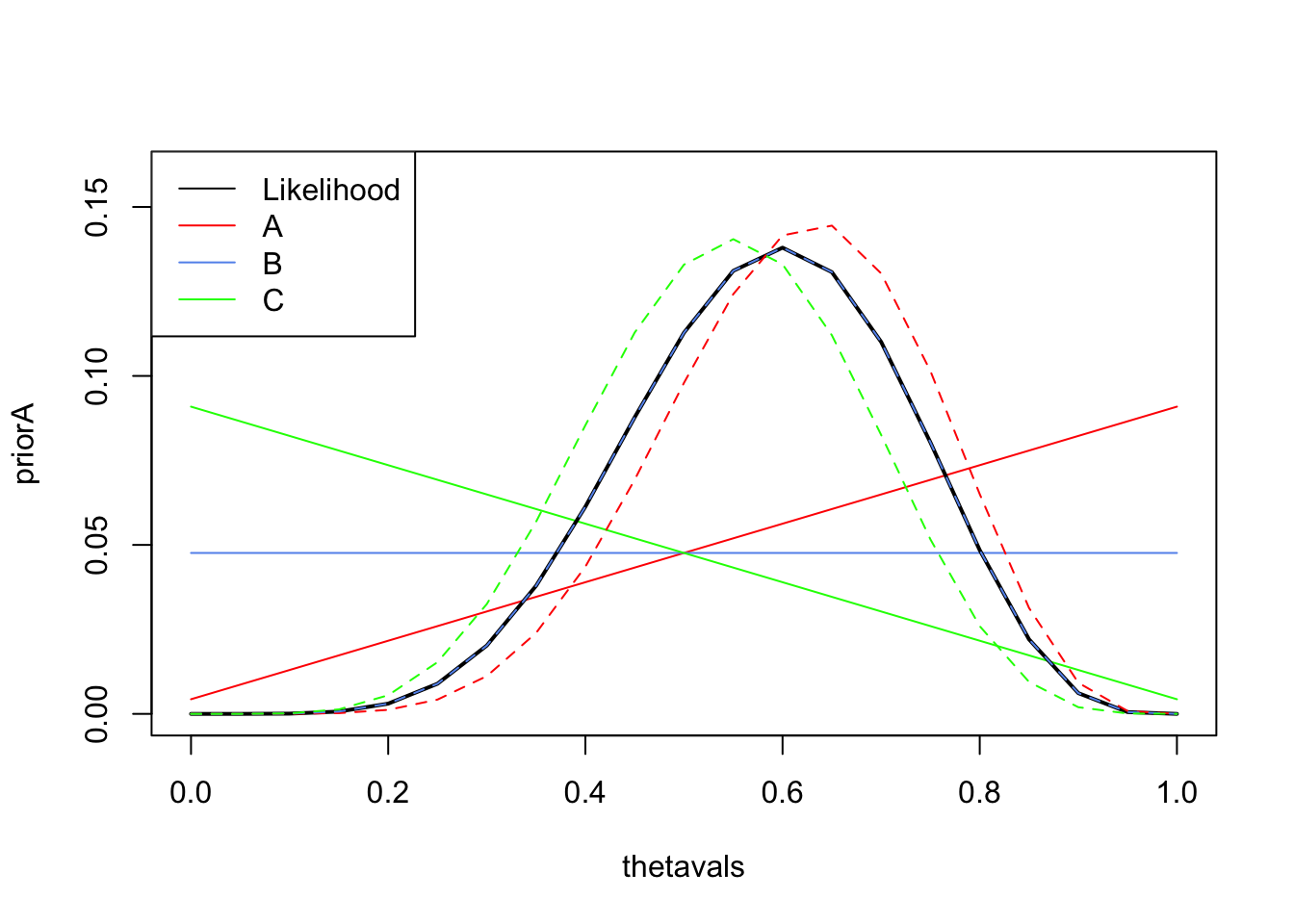
To begin with, let us suppose our prior beliefs consider it more likely that a current MP is re-elected than otherwise. One way of representing this, is to assign the following probability for the possible values \(\theta_i\) where \(i=1,\dots,21\): \[ P[\theta=\theta_i] = \frac{i}{231} \]

  • Create a vector priorA which contains the above prior probabilities for \(\theta\).
  • Plot priorA vertically against thetavals using plot, connecting the values with red lines and setting the range of the vertical axis to be \([0,0.16]\). Hint: see the Technique below.
  • Explain how this prior distribution represents the specific prior beliefs expressed above.

When plotting data with plot, we can change how plot draws the data by passing a type argument into the function. The type argument can take a number of different values to produce different types of plot

  • type="p" - draws a standard scatterplot with a “p”oint for every (x,y) pair
  • type="l" - connects adjacent (x,y) pairs with straight “l”ines, does not draw points. Note: l is a lowercase L, not the number 1.
  • type="b" - draws “b”oth points and connecting line segments
  • type="s" - connects points with “s”teps, rather than straight lines

We can further customize the appearance of the plot by supplying further arguments to plot:

3 The Likelihood

If \(X\) is the number of people who support the current MP in a sample of size \(n\) then \[ X \sim \text{Bin}(n,\theta) \] where \(\theta\) is the probability of a voter voting for the MP, and \[ P[X=x~|~\theta]~=~\binom{n}{x} \theta^x (1-\theta)^{n-x} \] This is our likelihood for \(x\) supporters from a sample of size \(n\).

  • From the sample above, what is the maximum likelihood estimate, \(\widehat{\theta}\), for \(\theta\)? (Hint: Think back to Term 1 and the MLE for a binomial parameter \(p\))

Recall from last term, we can create our own functions using the function syntax.

A function needs to have a name, usually at least one argument (although it doesn’t have to), a body of code that performs some computation, and usually returns an object or value. For example, a simple function that takes one argument \(x\) and computes and returns \(x^2\) is:

squareit <- function(x) {
  sq <- x^2 # square x
  return(sq) # return value 
}

Note that in R, you need to enclose the blocks of your code (a function body, the content of loops and if statements, etc) in curly braces { and }, whereas in Python you use indenting to indicate this.

We can use sapply to apply a given function to every element of a vector. For example, we can compute the squares of the first 10 integers using the above squareit function by evaluating the command

sapply(1:10, squareit)

If you’re familiar with Python’s list comprehensions, you’ll find that sapply performs a similar role in R.

  • Write an R function called like with one argument, theta, that computes and returns the binomial likelihood for a given value of \(\theta\) using the values of \(x\) and \(n\) for the data in our example. Hint: You can use the function choose to calculate \(\binom{a}{b}\).
  • Use sapply to evaluate your likelihood function for all the possible values thetavals, and save this as likeTheta.
  • Rescale the values of likeTheta so they sum to 1 (as a valid probability distribution should). Replace likeTheta by these normalised values.
  • Add the likelihood (likeTheta) to your plot using thick black lines.

4 The Posterior distribution

Given the prior and likelihood, all we need to compute the posterior distribution is the data probability in the denominator of Bayes theorem.
  • Use the likelihood, \(f(x~|~\theta)\), and prior, \(f(\theta)\) to compute the data probability by the partition theorem: \[ P[X] = \sum_\theta P[X~|~\theta] P[\theta] \]
  • Save this probability to pData. Hint: use the sum function.
  • Use Bayes theorem to combine the prior, likelihood and data probability to compute the posterior distribution for \(\theta\) given the data \(x\). Save this as postThetaA. \[ P[\theta~|~x] = \frac{P[X~|~\theta] P[\theta]}{P[X]} \]
  • Add the posterior distribution to your plot as dashed red lines. You should end up with a plot like the one below.
  • Compare the prior, posterior, and likelihood. How influential was the prior distribution for \(\theta\) in this case?
  • What is the most probable value of \(\theta\) given the sample? Is this the same or different to \(\widehat{\theta}\)? Why?

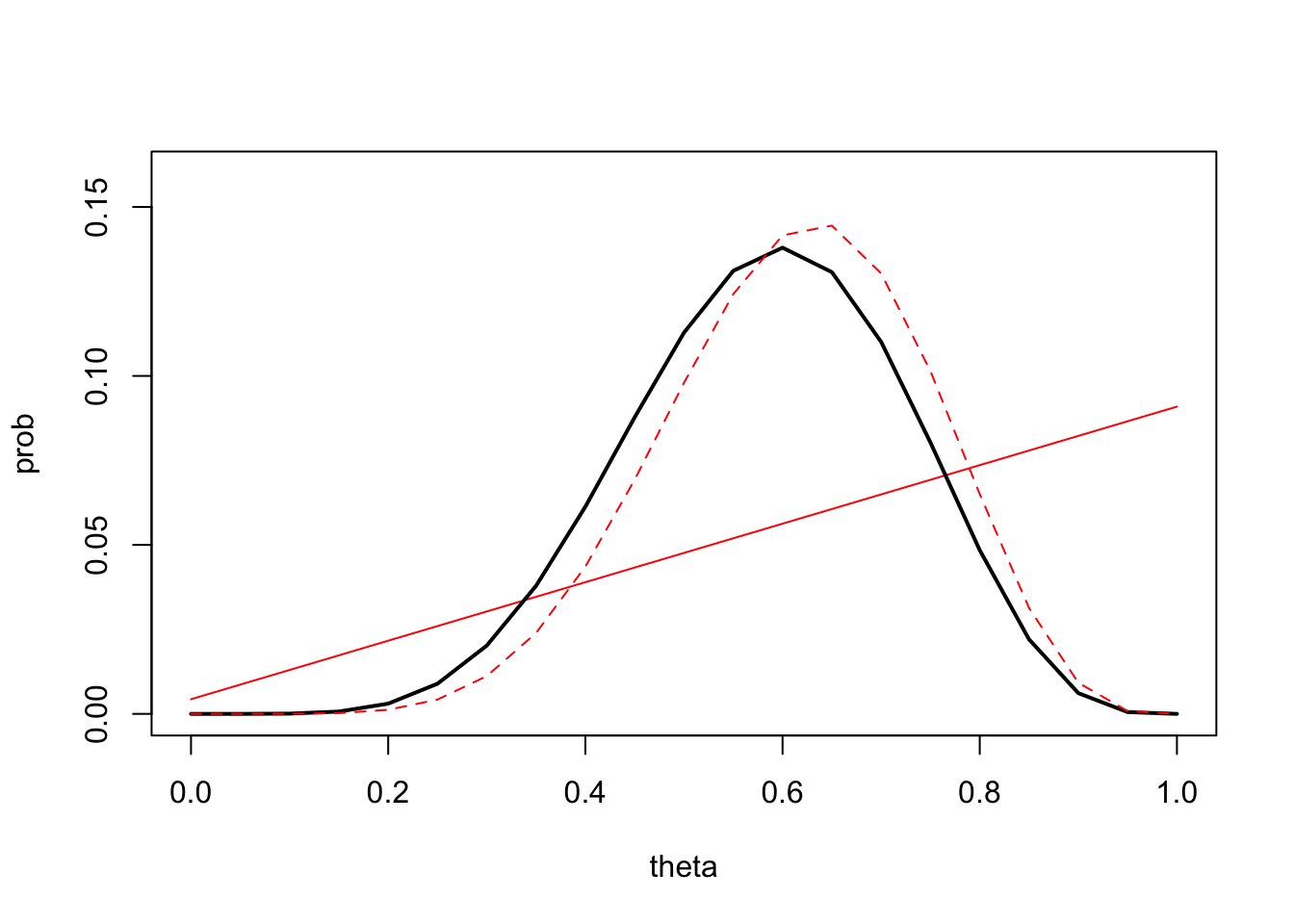
The simple prior for \(\theta\) has been transformed into something more interesting after updating by the data. It’s no longer a simple straight line, but has a similar shape to the likelihood albeit shifted slightly to the right. The posterior is a compromise between the prior information and the data information in the likelihood.

5 Exploring other prior distributions

Suppose now we consider two alternative prior distributions for \(\theta\):

  • Prior \(B\) is non-informative and considers all values of \(\theta\) to be equally likely: \[ P_B[\theta=\theta_i] = \frac{1}{21} \]
  • Prior \(C\) considers it more likely that voters will vote for an alternative candidate: \[ P_C[\theta=\theta_i] = \frac{22-i}{231} \]
  • Create two vectors priorB and priorC which contains the prior probabilities for \(\theta\) under both of these cases.
  • Use the lines function to add priorB and priorC to your plot using blue and green lines.
  • Compare the three prior distributions, and justify their shape in terms of the prior information they represent.
  • What do you expect the posterior distributions using priorB and priorC to look like? How will they differ to the posterior obtained above?

Now, let’s compute the posteriors under these new priors:

  • Repeat the Bayesian calculations of Exercise 4.1 to find the posterior distributions when using priorB and priorC as the prior distribution of \(\theta\). You will need to re-calculate \(P[X]\) and \(P[\theta~|~X]\) in both cases. Save the new posterior distributions as postThetaB and postThetaC.

The legend function adds a legend to a plot. The syntax is legend(location, legend, ...), and the required arguments are:

  • location: Where in the plot to draw the legend. The easier way to do this is using a keyword: e.g. "topleft", "top", "topright", "right", etc.
  • legend: A vector of strings with the labels for each item in the legend.

We can then draw a legend with labels to explain the different lines, points, and colours we are using in the plot, as appropriate. For example, the command

legend("topright",legend=c('Red Squares','Blue Circles'), pch=c(15,16),col=c('red','blue'))

will draw a legend on an existing plot on the top right of the plot with red squares appearing next to the text ‘Red Squares’ and blue circles next to the text ‘Blue Squares’.

  • Add postThetaB and postThetaC to your plot as blue and green dashed lines respectively.
  • Add a legend to your plot to label the likelihood and the three different cases of prior and posterior. You will need to set lty=1 to show lines in the legend, and use the col argument to specify the colours of the lines.
  • How do the posterior distributions compare to one another? Did the posterior distributions behave as you expected in the previous exercise?
  • Explain and justify any similarity/differences between \(P[X~|~\theta]\) using the original prior, and \(P_B[\theta~|~X]\) using prior B.