4 Problem Sheet 4:
Computations with Galois groups

Exercise 4.1 Let $K\subset M\subset L$ be a tower of finite extensions.

$\;(a)$ Given that $L/K$ is a Galois extension, prove that $L/M$ is as well.

$\;(b)$ Give an example where $L/K$ is Galois but $M/K$ is not.

Solution

$(a)$ We need to show $L/M$ is normal and separable:

As $L/K$ is normal, then it is the splitting field of some polynomial $f(x)\in K[x]$ over $K$ and there are $\theta_1,...,\theta_n\in L$ with $f(x)=c(x-\theta_1,...,\theta_n)$ and $L=K(\theta_1,...,\theta_n)$. Clearly, $f(x)\in M[x]$, $f(x)$ splits completely in $L[x]$ and $L=M(\theta_1,...,\theta_n)$. Hence $L$ is the splitting field of $f(x)$ over $M$ and $L/M$ is normal.
Any $\beta\in M$ is also in $L$, and as $L/K$ is separable, the minimal polynomial of $\beta$ over $K$ has no repeated roots. Hence $L/M$ is separable.

$(b)$ Consider the tower $K=\mathbb{Q} \;\subset\; M=\mathbb{Q}(\sqrt[3]{2}) \;\subset\; L=\mathbb{Q}(\sqrt[3]{2},\omega)$ where $\omega=e^{2\pi i/3}$.

Then $L/K$ is normal as it is the splitting field of $x^3-2$ over $\mathbb{Q}$.
However, $M/K$ is not normal, as it contains only one root of the irreducible polynomial $x^3-2\in\mathbb{Q}[x]$.

Exercise 4.2 Which of the following simple extensions $L/K$ are Galois? Give reasons.

$\;(a)\;$ $L=\mathbb{Q}(\sqrt[3]{2})$ over $K=\mathbb{Q},\hspace{5em}$ $\;(b)\;$ $L=\mathbb{Q}(\sqrt[4]{2})$ over $K=\mathbb{Q},$

$\;(c)\;$ $L=\mathbb{Q}(\sqrt[8]{2})$ over $K=\mathbb{Q}(\sqrt{2}),\hspace{2.85em}$ $\;(d)\;$ $L=K(\sqrt[8]{2})$ over $K=\mathbb{Q}(i),$

$\;(e)\;$ $L=\mathbb{F}_5(x)$ over $K=\mathbb{F}_5(x^4),\hspace{3.45em}$ $\;(f)\;$ $L=\mathbb{F}_p(x)$ over $K=\mathbb{F}_p(x^2)$ for $p$ prime,

$\;(g)\;$ $L=\mathbb{C}(x)$ over $K=\mathbb{C}(x^5),\hspace{4.05em}$ $\;(h)\;$ $L=\mathbb{F}_2(x)$ over $K=\mathbb{F}_2(x^4).$

Solution

$(a)$ This extension isn’t Galois as it isn’t normal.

The minimal polynomial of $\sqrt[3]{2}$ over $K=\mathbb{Q}$ is $x^3-2\in\mathbb{Q}[x]$. This has only one root in $L=\mathbb{Q}(\sqrt[3]{2})$.

$(b)$ This extension isn’t Galois as it isn’t normal.

The minimal polynomial of $\sqrt[4]{2}$ over $K=\mathbb{Q}$ is $x^4-2\in\mathbb{Q}[x]$. This has only two roots $\pm\sqrt[4]{2}$ in $L=\mathbb{Q}(\sqrt[4]{2})$.

$(c)$ This extension isn’t Galois as it isn’t normal.

The minimal polynomial of $\sqrt[8]{2}$ over $K=\mathbb{Q}(\sqrt{2})$ is $x^4-\sqrt{2}\in K[x]$. This has only two roots $\pm\sqrt[8]{2}$ in $L=\mathbb{Q}(\sqrt[8]{2})$.

$(d)$ This extension is Galois.

Note that $\zeta=e^{\pi i/4}=(1+i)/\sqrt{2}\in L=\mathbb{Q}(i,\sqrt[8]{2})$. The minimal polynomial of $\sqrt[8]{2}$ over $K=\mathbb{Q}(i)$ is $f(x)=x^8-2\in K[x]$. This has $8$ distinct roots $\zeta^kx\in L$ for $0\leq k\leq 7$ and $L$ is the splitting field of $f(x)$ over $K$.

$(e)$ This extension is Galois.

The minimal polynomial of $x$ over $K=\mathbb{F}_5(x^4)$ is $f(X)=X^4-x^4\in K[X]$. This has $4$ distinct roots $x, 2x, 3x, 4x\in L=\mathbb{F}_5(x)$ and $L$ is the splitting field of $f(X)$ over $K$.

$(f)$ This extension is Galois when $p\neq 2$ but not when $p=2$.

The minimal polynomial of $x$ over $K=\mathbb{F}_p(x^2)$ is $f(X)=X^2-x^2\in K[X]$. If $p\neq 2$, this has $2$ distinct roots $\pm x\in L=\mathbb{F}_p(x)$ and $L$ is the splitting field of $f(X)$ over $K$.
However, if $p=2$, $f(X)=X^2-x^2=(X-x)^2$ has repeated roots so the extension isn’t separable.

$(g)$ This extension is Galois.

The minimal polynomial of $x$ over $K=\mathbb{C}(x^5)$ is $f(X)=X^5-x^5\in \mathbb{C}[X]$. This has five roots $e^{2j\pi i/5}x\in L$ for $0\leq j\leq 4$ and $L$ is the splitting field of $f(X)$ over $K$.

$(h)$ This extension is not Galois as it isn’t separable.

The minimal polynomial of $x$ over $K=\mathbb{F}_2(x^4)$ is $f(X)=X^4-x^4\in K[X]$. This has repeated roots since $X^4-x^4=(X-x)^4$.

Exercise 4.3 $\;(a)$ Find a minimal Galois extension $L/\mathbb{Q}$ containing $\mathbb{Q}(\sqrt[4]{5})$.

$\;(b)$ Describe the structure of $G=\Gal(L/\mathbb{Q})$.

$\;(c)$ Find all the proper subgroups of $G$. Which ones are normal subgroups?

$\;(d)$ Find all intermediate fields $\mathbb{Q}\subset M\subset L$ with $[M:\mathbb{Q}]=2$ or $4$. Which are normal extensions of $\mathbb{Q}$?

Solution

This is a long question, but should be a good test that you’ve understood how to construct Galois groups and use the Fundamental Theorem.

$(a)$ As $\mathbb{Q}$ has characteristic zero, any extension is automatically separable. Let $\theta=\sqrt[4]{5}$. Then the minimal polynomial of $\theta$ over $\mathbb{Q}$ is $f(x)=x^4-5$. Any normal extension of $\mathbb{Q}$ containing $\mathbb{Q}(\theta)$ must contain the four roots $\pm\theta,\, \pm i\theta$ of $f(x)$. The splitting field $L$ of $f(x)$ over $\mathbb{Q}$ is by definition the minimal extension containing these roots and splitting fields are normal extensions. Clearly, $\theta$ and $i$ are in $L$, and $L=\mathbb{Q}(\sqrt[4]{5},i)$.

$(b)$ Since $\mathbb{Q}(\theta)\subset\mathbb{R}$, we have $i\not\in\mathbb{Q}(\theta)$ so $[L:\mathbb{Q}(\theta)]=2$.

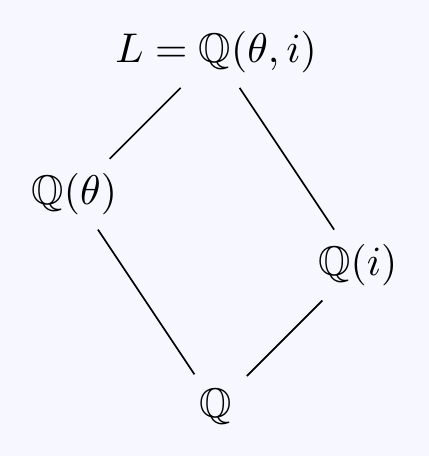
Since $[L:\mathbb{Q}]=[L:\mathbb{Q}(\theta)] [\mathbb{Q}(\theta):\mathbb{Q}]=2\times 4=8$, the Galois group $G=\Gal(L/\mathbb{Q})$ is a group of order $8$. We need to determine its structure.

$G$ contains the order $2$ subgroup $\Gal(L/\mathbb{Q}(\theta))$. This is generated by complex conjugation $\tau\in G$ where $\tau(i)=-i$ and $\tau(\theta)=\theta$. \[\Gal(L/\mathbb{Q}(\theta))=\{\id,\tau\}=\langle\,\tau\,\rangle\cong\mathbb{Z}/2.\]
$G$ contains the order $4$ subgroup $H=\Gal(L/\mathbb{Q}(i))$. This is generated by an automorphism $\sigma\in G$ where $\sigma(i)=i$ and $\sigma(\theta)=i\theta$. \[H=\Gal(L/\mathbb{Q}(i))=\{\id,\sigma,\sigma^2,\sigma^3\}=\langle\,\sigma\,\rangle\cong\mathbb{Z}/4.\]

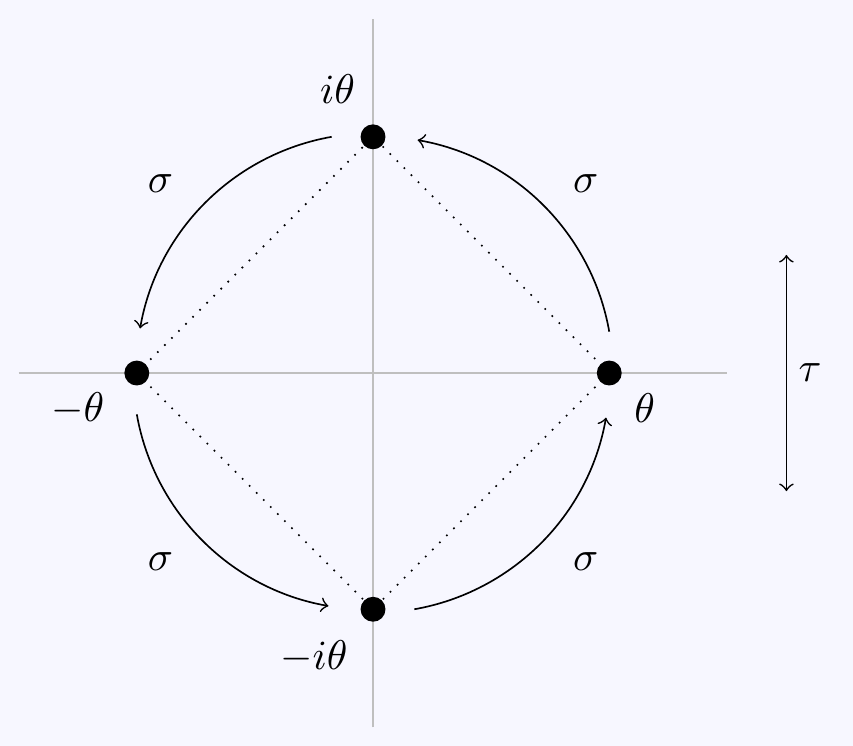
Now $L^H=\mathbb{Q}(i)$ is Galois over $\mathbb{Q}$ and as a result, $H$ is a normal subgroup of $G$. Since $|G|/|H|=2$ and $\tau\not\in H$, we see that $G$ is the disjoint union of two cosets $G=H\cup\tau H$ \[G=\{\id,\sigma,\sigma^2,\sigma^3,\tau,\tau\sigma, \tau\sigma^2,\tau\sigma^3\}.\] Notice these are distinct elements of $G$ since no two have the same effects on both $\theta$ and $i$. We clearly have $\tau^2=\sigma^4=\id$. There is also a relation $\sigma\tau=\tau\sigma^3$, which we check by seeing how each side acts on $\theta$ and $i$: \[\begin{cases}\;\;\sigma\tau(\theta)=\sigma(\theta)=i\theta \\ \;\;\sigma\tau(i)=\sigma(-i)=-i\end{cases} \qquad\text{and}\qquad \begin{cases}\;\;\tau\sigma^3(\theta)=\tau(-i\theta)=i\theta \\ \;\;\tau\sigma^3(i)=\tau(i)=-i\end{cases}\] Note we can use this to find the product of any two elements in $G$ (as another element in $G$). We could also write this relation as $\tau^{-1}\sigma\tau=\sigma^{-1}$ and we recognise that $G$ is isomorphic to the dihedral group $D_4$. \[G=\langle\,\sigma,\tau\,\mid\,\sigma^4=\tau^2=\id,\;\tau^{-1}\sigma\tau=\sigma^{-1}\,\rangle\cong D_4. \]

Remark: We can visualise $G$ as the symmetry group $D_4$ of a square by plotting the four roots in the complex plane and seeing how they are moved by $G$. Notice complex conjugation $\tau$ is a reflection of the whole field $L\subset\mathbb{C}$, However, the other automorphism $\sigma$ does not rotate the whole field as, for instance, rational numbers on the real line are not moved by $\sigma$. It is only rotating the 4 roots…

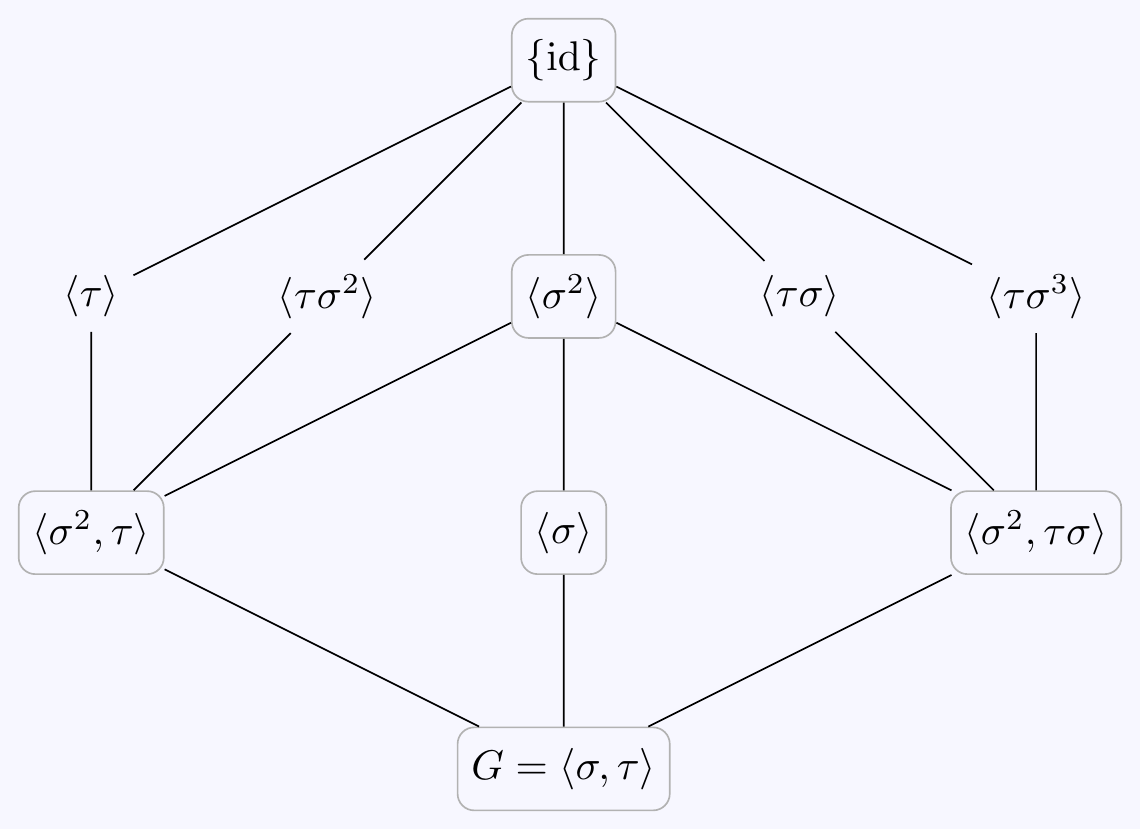
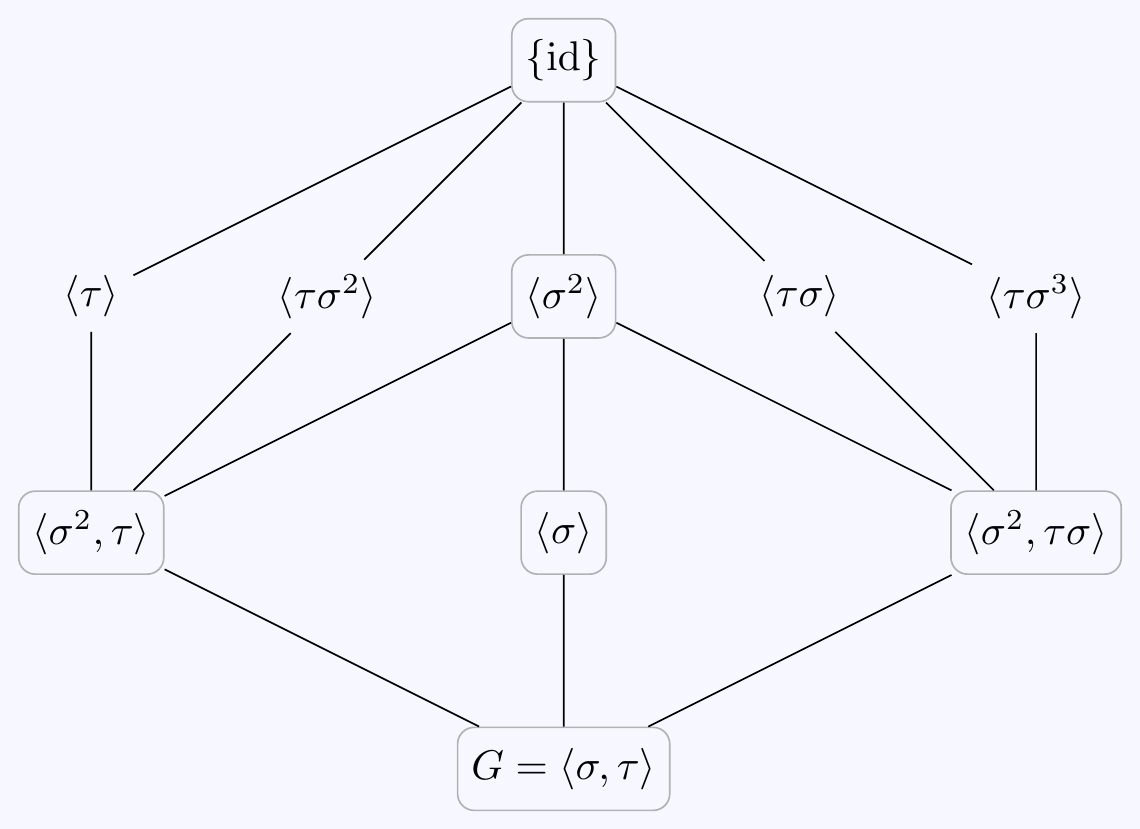
$(c)$ The proper subgroups of $D_4$ have order $2$ or $4$:

There are five elements of $G$ having order $2$ and each generates a subgroup isomorphic to $\mathbb{Z}/2$: \[\langle\,\sigma^2\,\rangle=\{\id,\sigma^2\},\quad \langle\,\tau\,\rangle=\{\id,\tau\},\] \[\langle\,\tau\sigma\,\rangle=\{\id,\tau\sigma\},\quad \langle\,\tau\sigma^2\,\rangle=\{\id,\tau\sigma^2\},\quad \langle\,\tau\sigma^3\,\rangle=\{\id,\tau\sigma^3\}\]
There are two elements of $G$ having order $4$, namely $\sigma$ and $\sigma^3=\sigma^{-1}$. These both generate the same subgroup isomorphic to $\mathbb{Z}/4$: \[H=\langle\,\sigma\,\rangle=\{\id,\sigma,\sigma^2,\sigma^3\}.\]
Any other subgroup of order $4$ must be isomorphic to $\mathbb{Z}/2\times\mathbb{Z}/2$. Such a subgroup has no order $4$ elements so cannot contain $\sigma$ or $\sigma^3$. However, it must contain $\sigma^2$ since the product of any two elements of the coset $\tau H$ gives an element in $H$. Therefore, it is generated by $\sigma^2$ and one of the order two elements in $\tau H$. There are two possibilities: \[\langle\,\sigma^2,\tau\,\rangle=\{\id,\sigma^2,\tau,\tau\sigma^2\},\quad \langle\,\sigma^2,\tau\sigma\,\rangle=\{\id,\sigma^2,\tau\sigma,\tau\sigma^3\}.\]

We’ll now find which of these are normal subgroups of $G$.

The order $4$ subgroups are automatically normal as they have index $2$ in $G$.
Also, $\tau\sigma^2=\sigma^2\tau$ so the the element $\sigma^2$ commutes with everything. That means the left and right cosets of $\langle\,\sigma^2\,\rangle$ are equal and this subgroup is normal in $G$.
However, the remaining four subgroups $\langle\,\tau\sigma^r\,\rangle$ for $r\in\mathbb{Z}$ are not normal in $G$. Indeed \[\sigma(\tau\sigma^r)\sigma^{-1}=\sigma\tau\sigma^{r-1}=\tau\sigma^3\sigma^{r-1}=\tau\sigma^{r+2}\not\in\langle\,\tau\sigma^r\,\rangle.\]

The full diagram of subgroups is as follows, with the normal ones being in boxes:

$(d)$ As $[L:\mathbb{Q}]=8$, the proper intermediate fields will have $[M:\mathbb{Q}]=2$ or $4$. By the Galois correspondence, they will be the fixed fields of the proper subgroups of $G$ we just described.

The order $4$ subgroups $\langle\sigma\rangle$, $\langle\sigma^2,\tau\rangle$, $\langle\sigma^2,\tau\sigma\rangle$ correspond to quadratic extensions of $\mathbb{Q}$ in $L$ so we just need to find a single degree $2$ element that is fixed.

We clearly have $L^{\langle\sigma\rangle}=\mathbb{Q}(i)$.
$\sigma^2(\theta)=\sigma(i\theta)=-\theta$ so $\sigma^2(\theta^2)=\theta^2$. Also $\tau(\theta^2)=\theta^2$, so $L^{\langle\sigma^2,\tau\rangle}=\mathbb{Q}(\theta^2)=\mathbb{Q}(\sqrt{5})$.
Similarly, $\sigma^2(i\theta^2)=i\theta^2$ and $\tau\sigma(i\theta^2)=i\theta^2$. Hence $L^{\langle\sigma^2,\tau\sigma\rangle}=\mathbb{Q}(i\theta^2)=\mathbb{Q}(i\sqrt{5})$.

The order $2$ subgroups correspond to degree $4$ extensions of $\mathbb{Q}$ in $L$. Some of these are easy to find, \[L^{\langle\,\tau\,\rangle}=\mathbb{Q}(\theta),\qquad L^{\langle\,\tau\sigma^2\,\rangle}=\mathbb{Q}(i\theta),\qquad L^{\langle\,\sigma^2\,\rangle}=\mathbb{Q}(\theta^2,i)=\mathbb{Q}(\sqrt{5},i).\] For the remaining subgroups $\langle\,\tau\sigma\,\rangle$ and $\langle\,\tau\sigma^3\,\rangle$, it’s less obvious which elements of $L$ are fixed. Consider how automorphisms in the subgroup act on a general element of $L$: \[\alpha=a+b\theta+c\theta^2+d\theta^3+ei+fi\theta+gi\theta^2+hi\theta^3 \quad\text{where $a,b,...,h\in\mathbb{Q}$.}\] Applying $\tau\sigma$ gives \[\tau\sigma(\alpha)=a-bi\theta-c\theta^2+di\theta^3-ei-f\theta+gi\theta^2+h\theta^3 \] so $\tau\sigma(\alpha)=\alpha$ if and only if $b=-f$, $c=-c$, $e=-e$, $d=h$, i.e. \[\alpha=a+b(1-i)\theta+d(1+i)\theta^3+gi\theta^2.\] Picking something simple, e.g. $a=d=g=0$ and $b=1$ gives a degree $4$ element $\beta=(1-i)\theta$ fixed by $\tau\sigma$. Actually, $\beta^2=-2i\theta^2$ and $\beta^3=-2(1+i)\theta^3$, so \[\tau\sigma(\alpha)=\alpha\quad\iff\quad \alpha=a+b\beta-(g/2)\beta^2-(d/2)\beta^3 \quad\text{for arbitrary $a,b,g,d\in\mathbb{Q}$.}\] Hence we have $L^{\langle\,\tau\sigma\,\rangle}=\mathbb{Q}(\beta)=\mathbb{Q}((1-i)\theta)$. Similarly, $\gamma=(1+i)\theta$ is fixed by $\tau\sigma^3$ and we find $L^{\langle\,\tau\sigma^3\,\rangle}=\mathbb{Q}((1+i)\theta)$. Here’s the full diagram of $L$ and its subfields, with the normal extensions of $\mathbb{Q}$ in boxes corresponding to the normal subgroups of $G$:

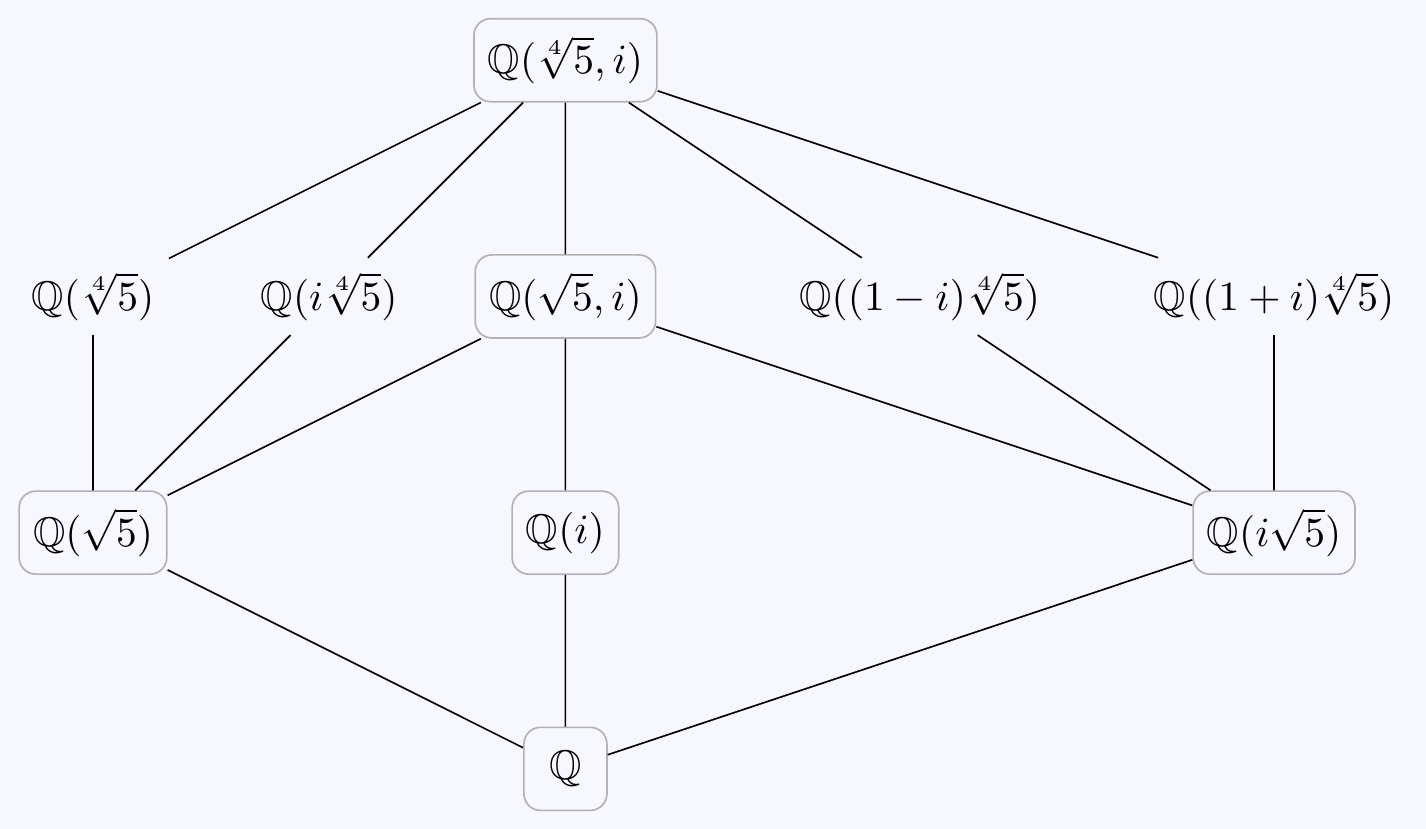
Notice that $\sigma\in G$ flips the non-normal extensions \[\mathbb{Q}(\sqrt[4]{5})\;\leftrightarrows\;\mathbb{Q}(i\sqrt[4]{5})\qquad\text{and}\qquad \mathbb{Q}((1-i)\sqrt[4]{5})\;\leftrightarrows\;\mathbb{Q}((1+i)\sqrt[4]{5}).\]

Exercise 4.4 Show that $\sqrt{7}\not\in L=\mathbb{Q}(\sqrt{2},\sqrt{3},\sqrt{5})$ by considering how automorphisms in the Galois group $\Gal(L/\mathbb{Q})$ act on $\sqrt{7}$.

Solution

We define three generators $\sigma_1,\sigma_2,\sigma_3\in G=\Gal(L/\mathbb{Q})$ via their actions on $\sqrt{2},\sqrt{3},\sqrt{5}$:

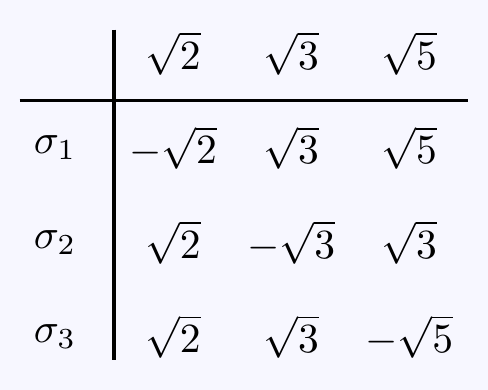
and then $G=\langle\,\sigma_1,\sigma_2,\sigma_3\,\mid\,\sigma_1^2=\sigma_2^2=\sigma_3^3=\id,\;\sigma_i\sigma_j=\sigma_j\sigma_i\;\; \text{for $1\leq i,j\leq 3$}\,\rangle\cong \mathbb{Z}/2\times\mathbb{Z}/2\times\mathbb{Z}/2$.

Consider the chain of subgroups and corresponding fixed fields \[\{\id\}\;\;\subset\;\;H_1=\langle\,\sigma_1\,\rangle\;\;\subset\;\; H_2=\langle\,\sigma_1,\sigma_2\,\rangle\;\;\subset\;\; G \] \[ L=\mathbb{Q}(\sqrt{2},\sqrt{3},\sqrt{5})\;\;\supset\;\; L^{H_1}=\mathbb{Q}(\sqrt{3},\sqrt{5}) \;\;\supset\;\; L^{H_2}=\mathbb{Q}(\sqrt{5})\;\;\supset\;\; L^G=\mathbb{Q}.\] Suppose that $\sqrt{7}\in L$. Then we have $\sigma(\sqrt{7})^2=\sigma(7)=7\;\;\Rightarrow\;\;\sigma(\sqrt{7})=\pm\sqrt{7}$ for each $\sigma\in G$.

Push $\sqrt{7}\in L$ down the tower to obtain two elements in $L^{H_1}=\mathbb{Q}(\sqrt{3},\sqrt{5})$:

Given $\sqrt{7}\in L$, we have \[\sigma_1(\sqrt{7})=\sqrt{7}\;\Rightarrow\;\sqrt{7}\in L^{H_1}\;\;\;\text{and}\;\;\;\sigma_1(\sqrt{7})=-\sqrt{7}\;\Rightarrow\;\sqrt{14}=\sqrt{2}\sqrt{7}\in L^{H_1}.\]

Now push each option $\sqrt{7},\sqrt{14}\in L^{H_1}$ down to $L^{H_2}=\mathbb{Q}(\sqrt{5})$:

Given $\sqrt{7}\in L^{H_1}=\mathbb{Q}(\sqrt{3},\sqrt{5})$, we have $\sqrt{21}=\sqrt{3}\sqrt{7}\in L^{H_1}$. Then \[\sigma_2(\sqrt{7})=\sqrt{7} \;\Rightarrow\; \sqrt{7}\in L^{H_2}\;\;\;\text{and}\;\;\;\sigma_2(\sqrt{7})=-\sqrt{7} \;\Rightarrow\; \sqrt{21}\in L^{H_2}.\]
Given $\sqrt{14}\in L^{H_1}=\mathbb{Q}(\sqrt{3},\sqrt{5})$, we have $\sqrt{42}=\sqrt{3}\sqrt{14}\in L^{H_1}$. Then \[\sigma_2(\sqrt{7})=\sqrt{7} \;\Rightarrow\; \sqrt{14}=\sqrt{2}\sqrt{7}\in L^{H_2}\;\;\;\text{and}\;\;\;\sigma_2(\sqrt{7})=-\sqrt{7} \;\Rightarrow\; \sqrt{42}=\sqrt{2}\sqrt{3}\sqrt{7}\in L^{H_2}\]

Finally push each option $\sqrt{7},\sqrt{21},\sqrt{14},\sqrt{42}\in L^{H_2}$ down to $L^G=\mathbb{Q}$:

Given $\sqrt{7}\in L^{H_2}$, we have $\sqrt{35}=\sqrt{5}\sqrt{7}\in L^{H_2}$. Then \[\sigma_3(\sqrt{7})=\sqrt{7} \;\Rightarrow\; \sqrt{7}\in L^{G}\;\;\;\text{and}\;\;\;\sigma_3(\sqrt{7})=-\sqrt{7} \;\Rightarrow\; \sqrt{35}=\sqrt{5}\sqrt{7}\in L^{G}.\]
Given $\sqrt{21}\in L^{H_2}$, we have $\sqrt{105}=\sqrt{5}\sqrt{21}\in L^{H_2}$. Then \[\sigma_3(\sqrt{7})=\sqrt{7} \;\Rightarrow\; \sqrt{21}\in L^{G}\;\;\;\text{and}\;\;\;\sigma_3(\sqrt{7})=-\sqrt{7} \;\Rightarrow\; \sqrt{105}=\sqrt{3}\sqrt{5}\sqrt{7}\in L^{G}.\]
Given $\sqrt{14}\in L^{H_2}$, we have $\sqrt{70}=\sqrt{5}\sqrt{14}\in L^{H_2}$. Then \[\sigma_3(\sqrt{7})=\sqrt{7} \;\Rightarrow\; \sqrt{14}\in L^{G}\;\;\;\text{and}\;\;\;\sigma_3(\sqrt{7})=-\sqrt{7} \;\Rightarrow\; \sqrt{70}=\sqrt{2}\sqrt{5}\sqrt{7}\in L^{G}.\]
Given $\sqrt{42}\in L^{H_2}$, we have $\sqrt{210}=\sqrt{5}\sqrt{42}\in L^{H_2}$. Then \[\sigma_3(\sqrt{7})=\sqrt{7} \;\Rightarrow\; \sqrt{42}\in L^{G}\;\;\;\text{and}\;\;\;\sigma_3(\sqrt{7})=-\sqrt{7} \;\Rightarrow\; \sqrt{210}=\sqrt{2}\sqrt{3}\sqrt{5}\sqrt{7}\in L^{G}.\]

We find that one of $\sqrt{7}, \sqrt{14},\sqrt{21},\sqrt{35},\sqrt{42},\sqrt{70},\sqrt{105},\sqrt{210}$ is a rational number. But this is false (e.g. by the rational root test) so the initial assumption $\sqrt{7}\in L$ gives a contradiction.

Remark: The above top-down step-by-step approach is instructive. However, looking back at it we can considerably speed up the argument as follows. We balance the $\pm$ signs to directly construct an irrational number fixed by all $\sigma_1, \sigma_2,\sigma_3$.

Suppose $\sqrt{7}\in L$. Then for each $1\leq i\leq 3$, we have \[\sigma_i(\sqrt{7})^2=\sigma_i(7)=7\qquad\implies\qquad \sigma_i(\sqrt{7})=(-1)^{j_i}\sqrt{7}\quad\text{for some integers $0\leq j_i\leq 1$.}\]
Define an integer $m=2^{j_1}3^{j_2}5^{j_3}$. Then we also have \[\sigma_i(\sqrt{m})=(-1)^{j_i}\sqrt{m}\qquad\implies\qquad \sigma_i(\sqrt{7m})=\sigma_i(\sqrt{7})\sigma_i(\sqrt{m})=\sqrt{7m}.\]
In particular, $\sqrt{7m}$ is fixed by all elements of $G$ and $\sqrt{7m}\in L^G=\mathbb{Q}$.

But $7m$ has exactly one prime factor of $7$ so is not a square in $\mathbb{Q}$. In other words, we have constructed an irrational number in $\mathbb{Q}$, giving the contradiction!

Exercise 4.5 $\;(a)$ Prove that $L=\mathbb{Q}\left(\sqrt{-3},\sqrt[3]{2},\sqrt[3]{5}\right)$ is Galois over $\mathbb{Q}$.

$\;(b)$ Let $K=\mathbb{Q}(\sqrt{-3})$. Show that $[L:K]=9$.

$\;(c)$ Find the structure of the group $H=\Gal\left(L/K\right)$.

$\;(d)$ Find all intermediate fields $K\subset M\subset L$ such that $[L:M]=3$.

$\;(e)$ Find the structure of the group $G=\Gal(L/\mathbb{Q})$.

Solution

$(a)$ Let $\omega=e^{2\pi i/3}=(-1+\sqrt{-3})/2$. Then $L=\mathbb{Q}(\sqrt{-3},\sqrt[3]{2},\sqrt[3]{5})=\mathbb{Q}(\omega,\sqrt[3]{2},\sqrt[3]{5})$ is the splitting field of \[(x^3-2)(x^3-5)=\left(x-\sqrt[3]{2}\right)\left(x-\omega\sqrt[3]{2}\right)\left(x-\omega^2\sqrt[3]{2}\right) \left(x-\sqrt[3]{5}\right)\left(x-\omega\sqrt[3]{5}\right)\left(x-\omega^2\sqrt[3]{5}\right)\] over $\mathbb{Q}$. Indeed, this field extension contains and is generated by $\sqrt[3]{2}, \sqrt[3]{5}$ and $\omega=(\omega\sqrt[3]{2})/\sqrt[3]{2}$. Thus $L/\mathbb{Q}$ is normal and, since the characteristic is zero, it is also separable and hence Galois.

$(b)$ We proceed similarly to the case of quadratic fields - things are only slightly more complicated. In the quadratic case, the square roots of unity $\pm 1$ are automatically in the base field. Here we make use of the cube roots of unity $1,\omega,\omega^2$ in $K$.

The extension $K(\sqrt[3]{2})/K$ is Galois (it’s the splitting field of $x^3-2$ over $K$ and has characteristic zero) and has degree at most $3$. Also, there is a non-trivial automorphism $\sigma\in\Gal(K(\sqrt[3]{2})/K)$ of order $3$ defined by $\sigma(\sqrt[3]{2})=\omega\sqrt[3]{2}$. Now $\Gal(K(\sqrt[3]{2})/K)=\langle\,\sigma\,\rangle\cong\mathbb{Z}/3$ and $[(K(\sqrt[3]{2}):K]=3$.

Suppose that $\sqrt[3]{5}\in K(\sqrt[3]{2})$. Then \[\sigma(\sqrt[3]{5})^3=\sigma(5)=5\quad\implies\quad \sigma(\sqrt[3]{5})=\sqrt[3]{5},\;\; \omega\sqrt[3]{5}\;\;\text{or}\;\;\omega^2\sqrt[3]{5}.\]

If $\sigma(\sqrt[3]{5})=\sqrt[3]{5}$ then $\sqrt[3]{5}\in K(\sqrt[3]{2})^{\langle\,\sigma\,\rangle}=K$ and so $\mathbb{Q}(\sqrt[3]{5})\subset K$.
If $\sigma(\sqrt[3]{5})=\omega\sqrt[3]{5}$ then $\sigma(\sqrt[3]{5/2})=(\omega\sqrt[3]{5})/(\omega\sqrt[3]{2})=\sqrt[3]{5/2}$ and $\mathbb{Q}(\sqrt[3]{5/2})=\mathbb{Q}(\sqrt[3]{20})\subset K$.
If $\sigma(\sqrt[3]{5})=\omega^2\sqrt[3]{5}$ then $\sigma(\sqrt[3]{5/4})=(\omega^2\sqrt[3]{5})/(\omega^2\sqrt[3]{4})=\sqrt[3]{5/4}$ and $\mathbb{Q}(\sqrt[3]{5/4})=\mathbb{Q}(\sqrt[3]{10})\subset K$.

In each case, we find a degree $3$ extension of $\mathbb{Q}$ contained in a degree $2$ extension $K/\mathbb{Q}$ which is impossible. Hence $x^3-5$ is irreducible over $K(\sqrt[3]{2})$ and \[ [L:K]=[L:K(\sqrt[3]{2})]\cdot[K(\sqrt[3]{2}):K]=3\cdot 3=9.\]

$(c)$ Define automorphisms $\sigma_1,\sigma_2\in H=\Gal(L/K)$ by their actions on $\sqrt[3]{2}$ and $\sqrt[3]{5}$ as follows (where we note they both act trivially on $\omega\in K$):

$\sigma_1(\sqrt[3]{2})=\omega\sqrt[3]{2}$ and $\sigma_1(\sqrt[3]{5})=\sqrt[3]{2}$. Then $\sigma_1^3=\id$ and we have an order $3$ subgroup \[H_1=\langle\,\sigma_1\,\rangle=\Gal(L/K(\sqrt[3]{5}))\subset H.\]
$\sigma_2(\sqrt[3]{2})=\sqrt[3]{2}$ and $\sigma_2(\sqrt[3]{5})=\omega\sqrt[3]{5}$. Then $\sigma_2^3=\id$ and we have an order $3$ subgroup \[H_2=\langle\,\sigma_2\,\rangle=\Gal(L/K(\sqrt[3]{2}))\subset H.\]

Note $\sigma_2\not\in\langle\sigma_1\rangle$ so $H_1$ and $H_2$ are different subgroups of $H$. Also, $\sigma_1\sigma_2=\sigma_2\sigma_1$ and we obtain $9$ distinct elements $\sigma_1^j\sigma_2^k\in H$ for $0\leq j,k\leq 2$. The Galois group is \[\begin{align*} H=\Gal(L/K)&=\{\sigma_1,\sigma_2\,\mid\, \sigma_1^3=\sigma_2^3=\id,\,\sigma_1\sigma_2=\sigma_2\sigma_1\} \\ &=\langle\,\sigma_1\,\rangle\times\langle\,\sigma_2\,\rangle\cong\mathbb{Z}/3\times\mathbb{Z}/3. \end{align*}\]

$(d)$ The intermediate fields with $[L:M]=3$ are the fixed fields of the order $3$ subgroups of $H$. As well as $H_1$ and $H_2$ above, there are two others: \[H_1=\langle\,\sigma_1\,\rangle, \quad H_2=\langle\,\sigma_2\,\rangle,\quad H_3=\langle\,\sigma_1\sigma_2\,\rangle,\quad H_4=\langle\,\sigma_1\sigma_2^2\,\rangle.\] Any order $3$ element in $H$ will generate exactly one of these four subgroups.

For the fixed fields, we already know $M_1=L^{H_1}=K(\sqrt[3]{5})$ and $M_2=L^{H_2}=K(\sqrt[3]{2})$. For the other two, compute fixed degree $3$ elements over $K$ as follows:

$\sigma_1\sigma_2(\sqrt[3]{2})=\omega\sqrt[3]{2}$ and $\sigma_1\sigma_2(\sqrt[3]{5})=\omega\sqrt[3]{5}$ so $\sigma_1\sigma_2(\sqrt[3]{20})=(\omega\sqrt[3]{2})^2(\omega\sqrt[3]{5})=\sqrt[3]{20}$.
$\sigma_1\sigma_2^2(\sqrt[3]{2})=\omega\sqrt[3]{2}$ and $\sigma_1\sigma_2^2(\sqrt[3]{5})=\omega^2\sqrt[3]{5}$ so $\sigma_1\sigma_2^2(\sqrt[3]{10})=(\omega\sqrt[3]{2})(\omega^2\sqrt[3]{5})=\sqrt[3]{10}$.

and so $M_3=L^{H_3}=K(\sqrt[3]{20})$ and $M_4=L^{H_4}=K(\sqrt[3]{10})$.

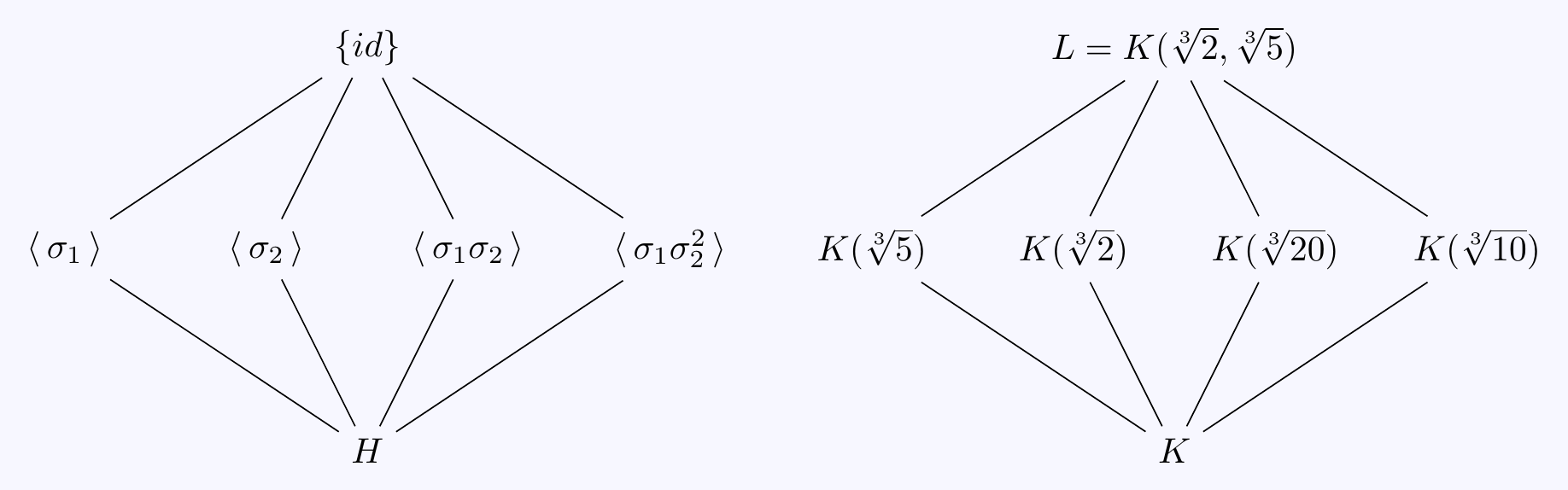
$(e)$ The group $H=\Gal(L/K)$ is a normal subgroup of $G=\Gal(L/\mathbb{Q})$ of index $2$. Define $\tau\in G$ by

$\tau(\omega)=\omega^2$ (equivalently, $\tau(\sqrt{-3})=-\sqrt{3}$) and $\tau(\sqrt[3]{2})=\sqrt[3]{2}$, $\tau(\sqrt[3]{5})=\sqrt[3]{5}$.

Then $H$ and $\tau H$ are disjoint cosets and we have $G=H\cup\tau H$ containing the $18$ distinct elements of the form $\sigma_1^j\sigma_2^k$ and $\tau\sigma_1^j\sigma_2^k$ where $0\leq j,k\leq 2$. We note that $G$ is not abelian - using $\tau(\omega)=\omega^2$, one can check how $\sigma_1\tau$, $\sigma_2\tau$ act on the field generators: \[\sigma_1\tau(\omega)=\omega^2=\tau\sigma_1^2(\omega),\quad \sigma_1\tau(\sqrt[3]{5})=\sqrt[3]{5}=\tau\sigma_1^2(\sqrt[3]{5})\] \[\text{and}\quad \sigma_1\tau(\sqrt[3]{2})=\omega\sqrt[3]{2}=\tau(\omega^2\sqrt[3]{2})=\tau\sigma_1^2(\sqrt[3]{2})\] so $\sigma_1\tau=\tau\sigma_1^2$ and similarly $\sigma_2\tau=\tau\sigma_2^2$. The full structure of $G=\Gal(L/\mathbb{Q})$ is given by \[G=\langle\,\sigma_1,\sigma_2,\tau\,\mid\, \sigma_1^3=\sigma_2^3=\tau^2=\id,\;\sigma_1\sigma_2=\sigma_2\sigma_1,\;\sigma_1\tau=\tau\sigma_1^2,\;\sigma_2\tau=\tau\sigma_2^2\,\rangle.\]

Remark: If you are interested, it turns out there are $5$ types of groups of order $18$.

$G$ is not isomorphic to $\mathbb{Z}/2\times\mathbb{Z}/3\times\mathbb{Z}/3$ or $\mathbb{Z}/2\times\mathbb{Z}/9$ as it is not abelian.
$G$ is not isomorphic to $D_9$ since $G$ doesn’t have any elements of order $9$.
$G$ is not isomorphic to $D_3\times\mathbb{Z}/3$. This group has a non-trivial centre - elements in the subgroup $\{id_{D_3}\}\times\mathbb{Z}/3$ commute with every element in the whole group. However, $G$ has trivial centre - the identity is the only element that commutes with all elements of the group.
Rather, $G$ is isomorphic to the fifth type: the generalised dihedral group of $H=\mathbb{Z}/3\times\mathbb{Z}/3$. One has $h\tau=\tau h^{-1}$ for every $h\in H$.

Exercise 4.6 In each of the following cases, for the field $K$ and polynomial $f(x)\in K[x]$, find the splitting field $L$ of $f(x)$ over $K$. Also find the Galois group $G=\Gal(L/K)$ and all the proper subgroups $H\subset G$.

$\;(a)\;\;K=\mathbb{Q}$ and $f(x)=(x^2-2)(x^2-5),\hspace{1em}$ $\;(b)\;\;K=\mathbb{Q}$ and $f(x)=(x^4+1)(x^2-5),$

$\;(c)\;\;K=\mathbb{Q}$ and $f(x)=x^5-1,\hspace{5.2em}$ $\;(d)\;\;K=\mathbb{Q}(i)$ and $f(x)=x^8-2,$

$\;(e)(\star)\;\;K=\mathbb{Q}$ and $f(x)=x^6-2,\hspace{3.9em}$ $\;(f)\;\;K=\mathbb{Q}(\sqrt{-3})$ and $f(x)=(x^3-2)(x^3-5),$

$\;(g)(\star)\;\;K=\mathbb{Q}$ and $f(x)=x^4+x^2-1,\hspace{1.7em}$ $\;(h)\;\;K=\mathbb{Q}(i)$ and $f(x)=x^8+1.$

Solution

$(a)$ The roots of $f(x)=(x^2-2)(x^2-5)$ are $\pm\sqrt{2},\pm\sqrt{5}$ and the splitting field is $L=\mathbb{Q}(\sqrt{2},\sqrt{5})$.

Define $\sigma,\tau\in G=\Gal(L/\mathbb{Q})$ by $\sigma(\sqrt{2})=-\sqrt{2}$, $\sigma(\sqrt{5})=\sqrt{5}$ and $\tau(\sqrt{2})=\sqrt{2}$, $\tau(\sqrt{5})=-\sqrt{5}$. Then \[G=\langle\,\sigma,\tau\,\mid\, \sigma^2=\tau^2=\id,\; \sigma\tau=\tau\sigma\,\rangle\cong\mathbb{Z}/2\times\mathbb{Z}/2.\] There are 3 proper subgroups, each isomorphic to $\mathbb{Z}/2$: \[H_1=\langle\,\sigma\,\rangle,\qquad H_2=\langle\,\tau\,\rangle,\qquad H_3=\langle\,\sigma\tau\,\rangle.\]

$(b)$ The roots of $f(x)=(x^4+1)(x^2-5)$ are $(\pm 1\pm i)/\sqrt{2}$ and $\pm\sqrt{5}$. We quickly see $i$ and $\sqrt{2}$ are linear combinations of these and the splitting field is $L=\mathbb{Q}(i,\sqrt{2},\sqrt{5})$.

Define $\sigma_1,\sigma_2,\sigma_3\in G=\Gal(L/\mathbb{Q})$ by their actions on $i,\sqrt{2},\sqrt{5}$:

$\sigma_1(\sqrt{i})=-\sqrt{i},\quad\sigma_1(\sqrt{2})=\sqrt{2},\quad\sigma_1(\sqrt{5})=\sqrt{5}$
$\sigma_2(\sqrt{i})=\sqrt{i},\quad\sigma_2(\sqrt{2})=-\sqrt{2},\quad\sigma_2(\sqrt{5})=\sqrt{5}$
$\sigma_3(\sqrt{i})=\sqrt{i},\quad\sigma_3(\sqrt{2})=\sqrt{2},\quad\sigma_3(\sqrt{5})=-\sqrt{5}$

Then check that \[G=\langle\,\sigma_1,\sigma_2,\sigma_3\,\mid\, \sigma_1^2=\sigma_2^2=\sigma_3^2=\id,\; \sigma_i\sigma_j=\sigma_j\sigma_i\;\text{for each $i,j$}\,\rangle\cong\mathbb{Z}/2\times\mathbb{Z}/2\times\mathbb{Z}/2.\] There are $7$ elements of order $2$, each giving a subgroup isomorphic to $\mathbb{Z}/2$: \[\langle\,\sigma_1\,\rangle,\;\; \langle\,\sigma_2\,\rangle,\;\; \langle\,\sigma_3\,\rangle,\;\; \langle\,\sigma_1\sigma_2\,\rangle,\;\; \langle\,\sigma_1\sigma_3\,\rangle,\;\; \langle\,\sigma_2\sigma_3\,\rangle,\;\; \langle\,\sigma_1\sigma_2\sigma_3\,\rangle.\] There are $7$ subgroups of order $4$, each isomorphic to $\mathbb{Z}/2\times\mathbb{Z}/2$. \[\langle\,\sigma_1,\sigma_2\,\rangle,\;\; \langle\,\sigma_1,\sigma_3\,\rangle,\;\; \langle\,\sigma_2,\sigma_3\,\rangle,\;\; \langle\,\sigma_1,\sigma_2\sigma_3\,\rangle,\;\; \langle\,\sigma_2,\sigma_1\sigma_3\,\rangle,\;\; \langle\,\sigma_3,\sigma_1\sigma_2\,\rangle,\;\; \langle\,\sigma_1\sigma_2,\sigma_2\sigma_3\,\rangle.\]

$(c)$ Let $\zeta=e^{2\pi i/5}$, so that \[\begin{align*} f(x)=x^5-1&=(x-1)(x^4+x^3+x^2+x+1) \\ &=(x-1)(x-\zeta)(x-\zeta^2)(x-\zeta^3)(x-\zeta^4) \end{align*}\] and the splitting field is $L=\mathbb{Q}(\zeta)$. Note we have $[L:\mathbb{Q}]=4$ as $g(x)=x^4+x^3+x^2+x+1$ is irreducible over $\mathbb{Q}$ (by using Eisenstein’s Criterion) and so $g(x)$ is the minimal polynomial of $\zeta$. Define

$\sigma\in G=\Gal(L/\mathbb{Q})$ by $\sigma(\zeta)=\zeta^2$. Then
$\sigma^2(\zeta)=\sigma(\zeta^2)=\zeta^4$,
$\sigma^3(\zeta)=\sigma(\zeta^4)=\zeta^8=\zeta^3$,
$\sigma^4(\zeta)=\sigma(\zeta^3)=\zeta^6=\zeta$ so $\sigma^4=\id$.

Thus we have $4$ distinct automorphisms $\id,\sigma,\sigma^2,\sigma^3$ and the Galois group is cyclic of order $4$: \[G=\{\id,\sigma,\sigma^2,\sigma^3\}=\langle\,\sigma\,\rangle\cong\mathbb{Z}/4.\] There is only one proper subgroup $\langle\,\sigma^2\,\rangle\cong\mathbb{Z}/2$ generated by the only order $2$ element $\sigma^2$.

$(d)$ Let $\theta=\sqrt[8]{2}$ and $\zeta=e^{\pi i/4}=(1+i)/\sqrt{2}$ so that the roots of $x^8-2$ are $\theta,\zeta\theta,\zeta^2\theta,...,\zeta^7\theta$.

Notice $\theta$ and $\zeta=(\zeta\theta)/\theta$ are in the splitting field. Furthermore, $\zeta^2=i$ and $i=\zeta\theta^4-1$, so the splitting field is \[L=\mathbb{Q}(\zeta,\theta)=\mathbb{Q}(i,\theta)=K(\theta).\] We have $[L:K]=8$ so need to find $8$ distinct automorphisms in the Galois group.

Define $\sigma\in\Gal(L/K)$ by $\sigma(\theta)=\zeta\theta$ and $\sigma(\zeta)=\zeta$. Notice this is a $K$-automorphism since $\zeta^2=i$ and $\sigma(i)=\sigma(\zeta^2)=\sigma(\zeta)^2=\zeta^2=i$.

Also, $\sigma^j(\theta)=\zeta^j\theta$ for $0\leq j\leq 7$ gives the $8$ distinct roots of $f(x)$. Hence $\sigma$ has order $8$ and the Galois group is cyclic or order $8$: \[\Gal(L/K)=\{\id,\sigma,\sigma^2,...,\sigma^7\}=\langle\,\sigma\,\rangle\cong\mathbb{Z}/8.\] This has two proper subgroups generated by the elements of order $2$ and $4$: \[\langle\,\sigma^2\,\rangle=\langle\,\sigma^6\,\rangle\cong\mathbb{Z}/4\quad\text{and}\quad \langle\,\sigma^4\,\rangle\cong\mathbb{Z}/2.\]

$(e)$ Let $\theta=\sqrt[6]{2}$ and $\zeta=e^{\pi i/3}=(1+\sqrt{-3})/2$. The roots of $f(x)=x^6-2$ are $\theta,\zeta\theta,...,\zeta^5\theta$ and the splitting field is \[L=\mathbb{Q}(\theta,\zeta)=\mathbb{Q}(\theta,\sqrt{-3}).\] To check the degree of $L/\mathbb{Q}$, notice $\sqrt{-3}$ is not real so $\sqrt{-3}\not\in\mathbb{Q}(\theta)$. Hence \[[L:\mathbb{Q}]=[L:\mathbb{Q}(\theta)] [\mathbb{Q}(\theta):\mathbb{Q}]=2\cdot6=12.\] Define $\sigma,\tau\in G=\Gal(L/\mathbb{Q})$ by their actions on $\theta$ and $\sqrt{-3}$:

$\sigma(\theta)=\zeta\theta$ and $\sigma(\sqrt{-3})=\sqrt{-3}$ (or equivalently $\sigma(\zeta)=\zeta$),
$\tau(\theta)=\theta$ and $\tau(\sqrt{3})=-\sqrt{3}$ (or equivalently $\tau(\zeta)=\zeta^{-1}=(1-\sqrt{-3})/2$).

Then $\sigma$ has order $6$ so we have a subgroup $H=\langle\,\sigma\,\rangle\subset G$ of order $6$. as well as a subgroup $\langle\,\tau\,\rangle\in G$ of order $2$. Note that $\tau\not\in H$ since $\tau$ fixes $\theta$, so the cosets $H$ and $\tau H$ are disjoint. We have $12$ distinct automorphisms $\sigma^j, \tau\sigma^j$ for $0\leq j\leq 5$.

Furthermore, there is a relation $\sigma\tau=\tau\sigma^{-1}$ since \[\sigma\tau(\theta)=\sigma(\theta)=\zeta\theta=\tau(\zeta^{-1}\theta)=\tau\sigma^{-1}(\theta),\] \[\sigma\tau(\zeta)=\sigma(\zeta^{-1})=\zeta^{-1}=\tau(\zeta)=\tau\sigma^{-1}(\zeta).\] Hence $G$ is isomorphic to the dihedral group $D_6$ of order $12$, i.e. the symmetry group of a regular hexagon. \[G=\langle\,\sigma,\tau\,\mid\,\sigma^6=\tau^2=\id,\;\tau^{-1}\sigma\tau=\sigma^{-1}\,\rangle\cong D_6. \]

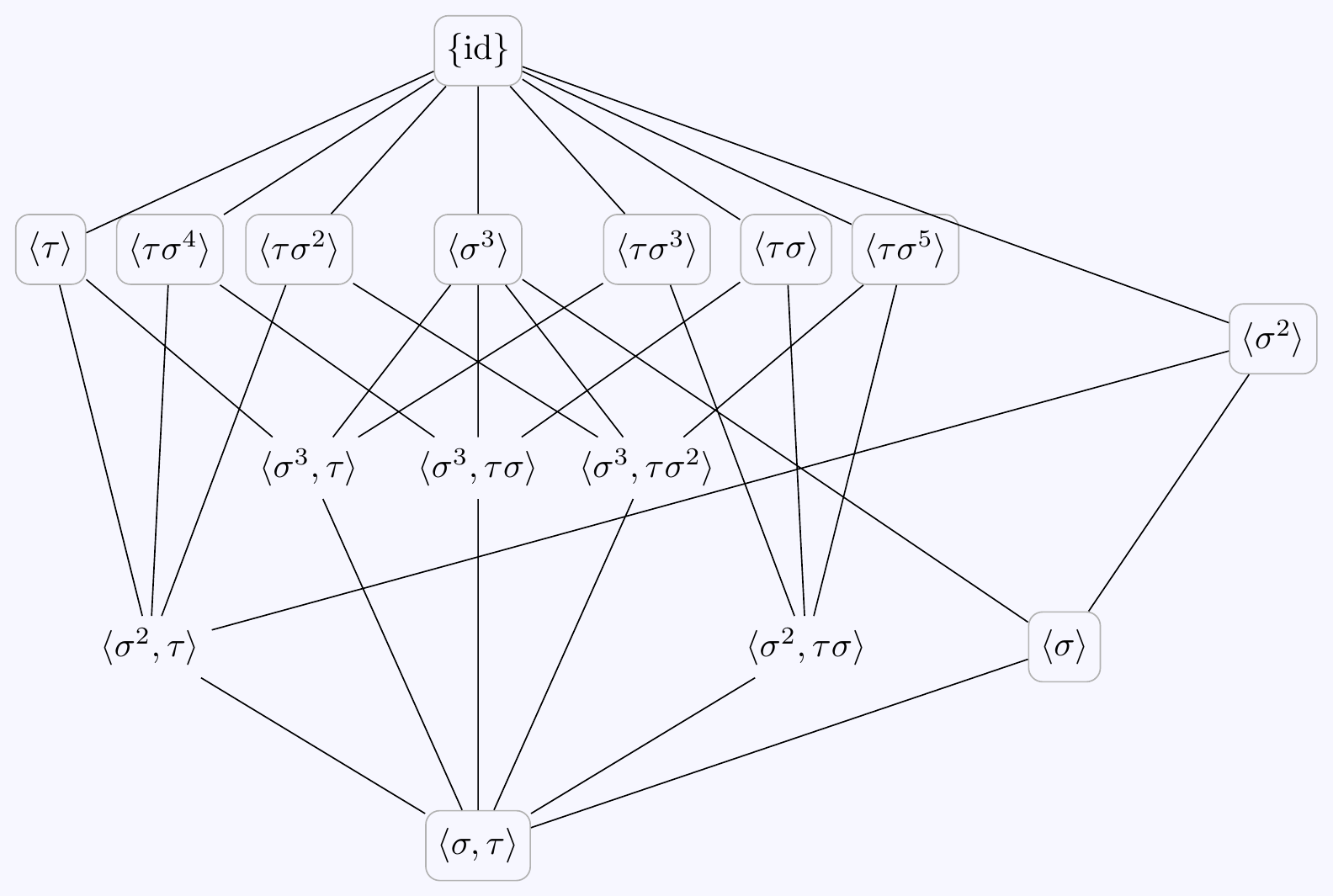
The are seven subgroups isomorphic to $\mathbb{Z}/2$. They are generated by the seven order $2$ elements: \[\langle\,\sigma^3\rangle\quad\text{and}\quad \langle\,\tau\sigma^j\,\rangle\quad\text{for $0\leq j\leq 5$}.\]
There is one subgroup of isomorphic to $\mathbb{Z}/3$. It is generated by the only element of order $3$: \[\langle\,\sigma^2\,\rangle\]
There are three subgroups of order $4$ isomorphic to $\mathbb{Z}/2\times\mathbb{Z}/2$. There are no elements of order $4$, so we need two order $2$ elements. These cannot both be from the coset $\tau H$ so must include $\sigma^3$ and we get \[\langle\,\sigma^3,\tau\rangle=\{\id,\sigma^3,\tau,\tau\sigma^3\},\quad \langle\,\sigma^3,\tau\sigma\rangle=\{\id,\sigma^3,\tau\sigma,\tau\sigma^4\},\quad \langle\,\sigma^3,\tau\sigma^2\rangle=\{\id,\sigma^3,\tau\sigma^2,\tau\sigma^5\}.\]
There are three subgroups of order $6$. They each must include the only order $3$ element $\sigma^2$. There is the abelian subgroup $H=\langle\,\sigma\,\rangle\cong\mathbb{Z}/6$. We also have \[\langle\,\sigma^2,\tau\rangle=\{\id,\sigma^2,\sigma^4,\tau,\tau\sigma^2,\tau\sigma^4\}\;\;\;\text{and}\;\;\; \langle\,\sigma^2,\tau\sigma\rangle=\{\id,\sigma^2,\sigma^4,\tau\sigma,\tau\sigma^3,\tau\sigma^5\}\] which are both isomorphic to $S_3\cong D_3$. (Notice they are not abelian.)

Just for fun, here’s the diagram of subgroups, with the normal ones in boxes. See if you can find some of the corresponding fixed fields…

$(f)$ Let $\omega=e^{2\pi i/3}=(-1+\sqrt{-3})/2\in K$, then the roots of $f(x)=(x^3-2)(x^3-5)$ are $\sqrt[3]{2},\omega\sqrt[3]{2},\omega^2\sqrt[3]{2}$ and $\sqrt[3]{5},\omega\sqrt[3]{5},\omega^2\sqrt[3]{5}$. The splitting field is \[L=\mathbb{Q}(\omega,\sqrt[3]{2},\sqrt[3]{5})=K(\sqrt[3]{2},\sqrt[3]{5}).\] Note we have $[L:K]=9$, by showing $\sqrt[3]{5}\not\in\mathbb{Q}(\sqrt[3]{2})$ as in the lecture notes.

Define $\sigma,\tau\in G=\Gal(L/K)$ by $\sigma(\sqrt[3]{2})=\omega\sqrt{2}$, $\sigma(\sqrt[3]{5})=\sqrt[3]{5}$ and $\tau(\sqrt[3]{2})=\sqrt[3]{2}$, $\tau(\sqrt[3]{5})=\omega\sqrt[3]{5}$. Then \[G=\langle\,\sigma,\tau\,\mid\, \sigma^3=\tau^3=\id,\; \sigma\tau=\tau\sigma\,\rangle\cong\mathbb{Z}/3\times\mathbb{Z}/3.\]

There are four subgroups of order $3$: \[\langle\,\sigma\,\rangle=\{\id,\sigma,\sigma^2\},\quad \langle\,\tau\rangle=\{\id,\tau,\tau^2\},\quad \langle\,\sigma\tau\rangle=\{\id,\sigma\tau,\sigma^2\tau^2\},\quad \langle\,\sigma\tau^2\rangle=\{\id,\sigma\tau^2,\sigma^2\tau\}.\]

$(g)$ We found this splitting field in Exercise 3.1(d), but let’s repeat some of the work:

We have $f(x)=x^4+x^2-1=(x^2-\alpha)(x^2-\beta)$ where $\begin{cases} \alpha=(-1+\sqrt{5})/2, \\ \beta=(-1-\sqrt{5})/2.\end{cases}$.

Notice that $\alpha\beta=-1$ so if we let \[\theta=\sqrt{\alpha}=\sqrt{(-1+\sqrt{5})/2}\] then the four roots are $\pm\theta$ and $\pm i/\theta$. In particular, the splitting field is $L=\mathbb{Q}(\theta,i)$. We saw in Exercise 3.1(d) that $f(x)$ is irreducible over $\mathbb{Q}$. (Another way to see this is to notice it is irreducible modulo $3$.) This means $[\mathbb{Q}(\theta):\mathbb{Q}]=4$ and since $\theta$ is real, $i\not\in\mathbb{Q}(\theta)$ and $[L:\mathbb{Q}(\theta)]=2$. Hence $[L:\mathbb{Q}]=8$ and the Galois group $G=\Gal(L/\mathbb{Q})$ has order $8$. We have the following familiar diagram

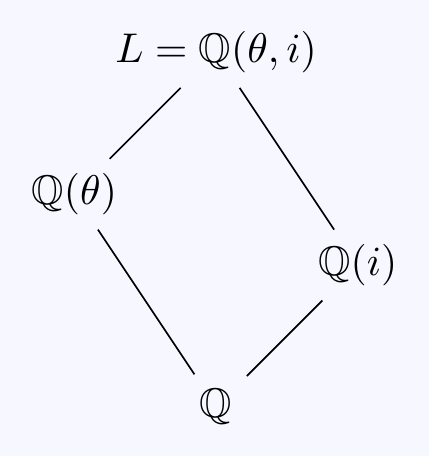
Any $\varphi\in\Gal(L/K)$ is determined by $\varphi(i)$ and $\varphi(\theta)$. Furthermore, there are two choices for $\varphi(i)=\pm i$ and four choices for $\varphi(\theta)=\pm\theta, \pm i/\theta$. As $G=\Gal(L/\mathbb{Q})$ has order $[L:\mathbb{Q}]=8$, all these choices must arise from some $\varphi$:

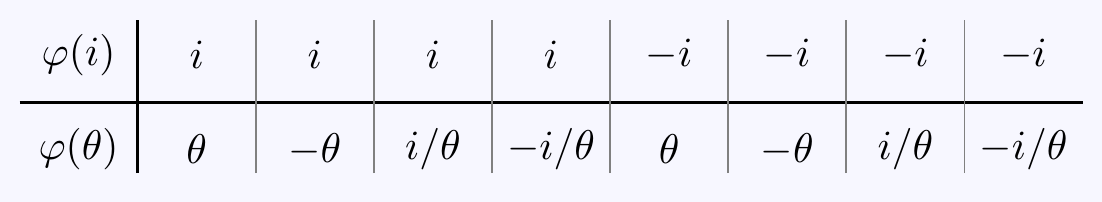
Column 5 is complex conjugation on $L=\mathbb{Q}(i,\theta)$.The only way to get an order $4$ element of $G$ is to choose one of the last two columns (none of the choices with $\varphi(i)=+i$ or $\varphi(\theta)=\pm\theta$ work). So define $\tau$ and $\sigma\in G$ by

$\tau(i)=-i$ and $\tau(\theta)=\theta$. This is order $2$ so gives $\langle\,\tau\,\rangle\cong\mathbb{Z}/2$.
$\sigma(i)=-i$ and $\sigma(\theta)=i/\theta$. Notice $\sigma^2(\theta)=\sigma(i/\theta)=-i/(i/\theta)=-\theta$ and $\sigma^4(\theta)=\theta$ so we do indeed have $\langle\,\sigma\,\rangle\cong\mathbb{Z}/4$.

Also, check that $\sigma\tau=\tau\sigma^3$ and so $G$ is isomorphic to the dihedral group $D_4$: \[G=\langle\,\sigma,\tau\,\mid\,\sigma^4=\tau^2=\id,\;\tau^{-1}\sigma\tau=\sigma^{-1}\,\rangle\cong D_4. \]

The subgroups are exactly as in Exercise 4.3:

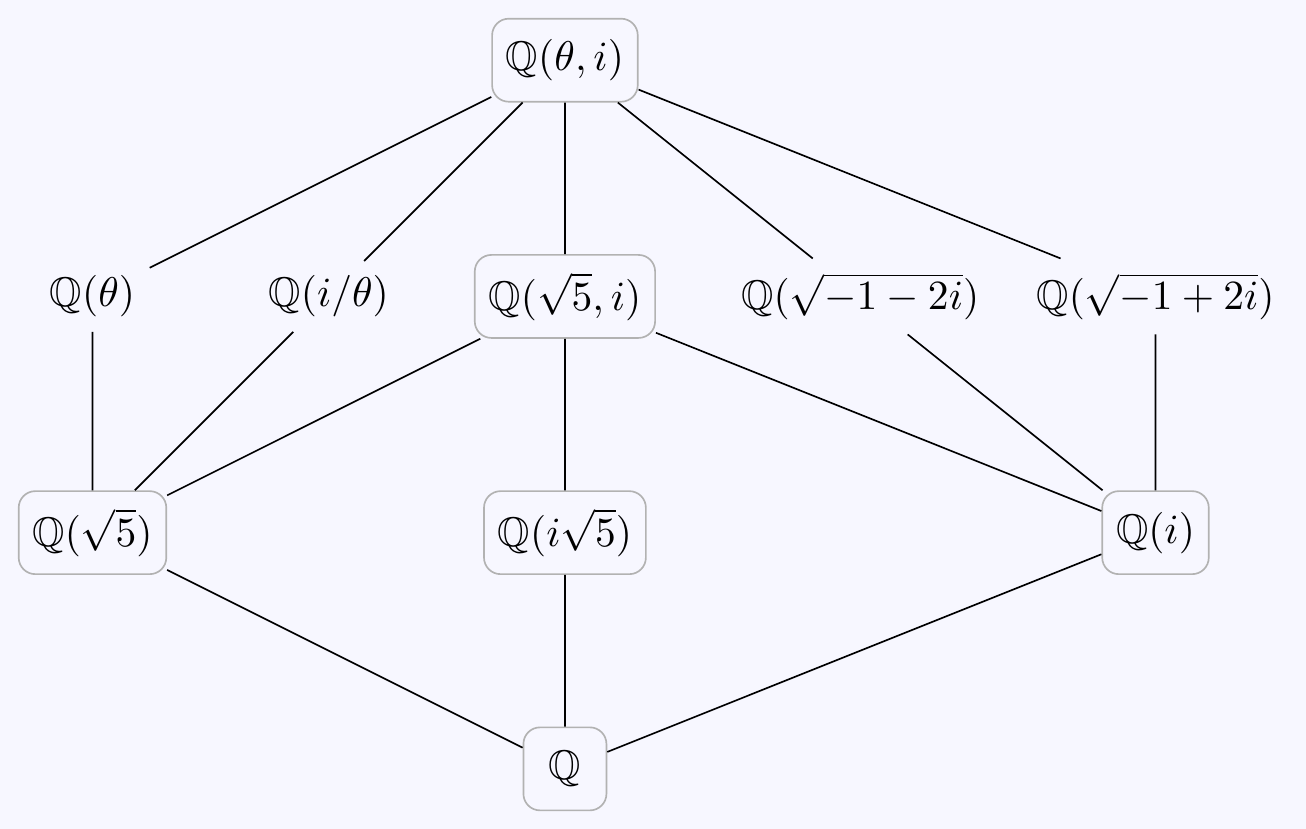
Remark: The question doesn’t ask for this, but it’s a useful exercise to try to find the corresponding fixed fields. This is similar to Exercise 4.3 - one has to find subextensions of the correct degree that are fixed by each subgroup. There are some subtle differences, however. For instance, for the subgroup $\langle\,\tau\sigma\,\rangle$, we find $\tau\sigma(\theta-i/\theta)=\tau\sigma(\theta)-\tau\sigma(i/\theta)=\tau(i/\theta)-\tau(-\theta)=-i/\theta+\theta$.

Furthermore,
\[\left(\theta-\frac{i}{\theta}\right)^2=\theta^2-2i-\frac{1}{\theta^2}=\frac{-1+\sqrt{5}}{2}-2i+\frac{-1-\sqrt{5}}{2}=-1-2i\] and $\theta-i/\theta=\sqrt{-1-2i}$ which is of degree $4$ over $\mathbb{Q}$. Thus $L^{\langle\,\tau\sigma\,\rangle}=\mathbb{Q}(\sqrt{-1-2i})$.

The full diagram of subfields is as follows, with the normal extensions of $\mathbb{Q}$ in boxes:

$(h)$ Let $\zeta=e^{\pi i/8}$ so $\zeta^8=-1$. Then the roots of $f(x)=x^8+1$ are $\pm\zeta, \pm\zeta^3, \pm\zeta^5,\pm\zeta^7$, i.e. the primitive $16th$ roots of unity. Hence the splitting field is $L=\mathbb{Q}(\zeta)=K(\zeta)$.

The minimal polynomial of $\zeta$ over $K=\mathbb{Q}(i)$ is \[x^4-i=(x-\zeta)(x+\zeta)(x-i\zeta)(x+i\zeta)\] so $[L:K]=4$. Define $\sigma\in\Gal(L/K)$ by

$\sigma(\zeta)=i\zeta=\zeta^5$. Note that $\sigma(i)=\sigma(\zeta^4)=(i\zeta)^4=i$ so this is a $K$-automorphism.
Then $\sigma^2(\zeta)=-\zeta$, $\sigma^3(\zeta)=-i\zeta$ and $\sigma^4=\id$. In other words, \[\Gal(L/K)=\{\id,\sigma,\sigma^2,\sigma^3\}=\langle\,\sigma\,\rangle\cong\mathbb{Z}/4.\]
The only proper subgroup is $\{\id,\sigma^2\}=\langle\,\sigma^2\,\rangle\cong\mathbb{Z}/2$.

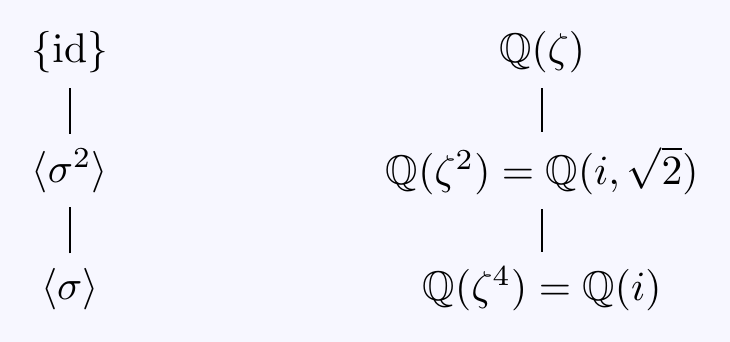
Exercise 4.7 Let $K$ be a field with $\ch(K)\neq 2$.

$\;(a)$ Given $a,b\in K$, show that $[K(\sqrt{a},\sqrt{b}):K]=4$ if and only if $a,b,ab\not\in{K^\times}^2$.

$\;(b)$ We say a set $\{a_1,...,a_n\}\subset K^\times$ is independent modulo squares when \[m_i\in\mathbb{Z}\;\;\text{and}\;\; a_1^{m_1}a_2^{m_2}\cdots a_n^{m_n}\in {K^\times}^2\;\;\implies\;\;\text{all $m_i$ are even}.\] $\;\;\;\;\,$ Let $L=K(\sqrt{a_1},\sqrt{a_2},...,\sqrt{a_n})$ for some $a_i\in K$. Prove by induction that $[L:K]=2^n$ if and only if $\{a_1,...,a_n\}$ is independent modulo squares.

$\;(c)$ In that case, show that $L/K$ is Galois with $\Gal(L/K)=\underbrace{\mathbb{Z}/2\times\cdots\times\mathbb{Z}/2}_\text{$n$ times}$.

Solution

$(a)$ For the “if” part, use a contrapositive proof:

if $a\in {K^\times}^2$, then $K(\sqrt{a},\sqrt{b})=K(\sqrt{b})$.
if $b\in {K^\times}^2$, then $K(\sqrt{a},\sqrt{b})=K(\sqrt{a})$.
if $ab\in {K^\times}^2$, then $\sqrt{b}=c/\sqrt{a}$ for some $c\in K$ so $K(\sqrt{a},\sqrt{b})=K(\sqrt{a})$.
In each case, we have $[K(\sqrt{a},\sqrt{b}):K]\leq 2<4$.

For the “only if” part, suppose that $a,b,ab\not\in {K^\times}^2$. Then $\sqrt{a}\not\in K$ implies $[K(\sqrt{a}):K]=2$. Now $K(\sqrt{a})/K$ is a quadratic Galois extension where $\Gal(K(\sqrt{a})/K)=\langle\,\sigma\,\rangle$ and $\sigma(\sqrt{a})=-\sqrt{a}$. Furthermore, if $\sqrt{b}\in K(\sqrt{a})$ then $\sigma(\sqrt{b})=\pm\sqrt{b}$ but

$\sigma(\sqrt{b})=\sqrt{b}\;\;\Rightarrow\;\;\sqrt{b}\in K(\sqrt{a})^{\langle\,\sigma\rangle}=K$.
$\sigma(\sqrt{b})=-\sqrt{b}\;\;\Rightarrow\;\;\sqrt{ab}\in K(\sqrt{a})^{\langle\,\sigma\rangle}=K$.

These both contradict the assumptions and we must have $\sqrt{b}\not\in K(\sqrt{a})$. In particular, $[K(\sqrt{a},\sqrt{b}):K(\sqrt{a})]=2$ and the Tower Law shows $[K(\sqrt{a},\sqrt{b}):K]=4$.

$(b)$ We show the “if” part by a contrapositive proof again. Suppose that $\{a_1,...,a_n\}\subset K^\times$ are not independent modulo squares. Then there exists $m_1,...m_n\in\mathbb{Z}$ not all even with \[a_1^{m_1}\cdots a_n^{m_n}=b^2\quad\text{for some $b\in K^\times$.}\] Without loss of generality, we can assume $m_n$ is odd, say $m_n=2k-1$ for $k\in\mathbb{Z}$. Then \[b\sqrt{a_n}=(\sqrt{a_1})^{m_1}\cdots (\sqrt{a_{n-1}})^{m_{n-1}} a_n^k\in K(\sqrt{a_1},...,\sqrt{a_{n-1}})\] and so $L=K(\sqrt{a_1},...,\sqrt{a_{n-1}})$. But then $[L:K]\leq 2^{n-1}$ and so $[L:K]\neq 2^n$.

To prove the “only if” part, we proceed by induction on $n$ using an argument as in part $(a)$.

Suppose $\{a_1,...,a_n\}\subset K^\times$ is independent modulo squares. In fact, we will answer part (c) at the same time by showing $L_n=K(\sqrt{a_1},...,\sqrt{a_n})$ is a Galois extension of $K$ with \[\Gal(L_n/K)=\langle\sigma_1\rangle\times\cdots\times\langle\sigma_n\rangle\cong \underbrace{\mathbb{Z}/2\times\cdots\times\mathbb{Z}/2}_\text{$n$ times}\] where $\sigma_i(\sqrt{a_i})=-\sqrt{a_i}$ and $\sigma_i(\sqrt{a_j})=\sqrt{a_j}$ for $j\neq i$. Notice that this will imply that $[L_n:K]=2^n$ as required. Assume the claim is true for $L_{n-1}=K(\sqrt{a_1},...,\sqrt{a_{n-1}})$ and suppose that $\sqrt{a_n}\in L_{n-1}$.

Then $\sigma_i(\sqrt{a_n})=(-1)^{m_i}\sqrt{a_n}$ for some $m_i\in\{0,1\}$ for each $1\leq i\leq n-1$.
Consider the element $\alpha=\sqrt{a_1^{m_1}\cdots a_{n-1}^{m_{n-1}}a_n}\in L_{n-1}$. For each $i$, we have \[\sigma_i(\alpha)=\sigma_i(\sqrt{a_1})^{m_1}\cdots\sigma_i(\sqrt{a_{n-1}})^{m_{n-1}}\sigma_i(\sqrt{a_n})=\alpha.\] In particular, $\alpha$ is fixed by each generator $\sigma_i\in\Gal(L_{n-1}/K)$ so is in the fixed field $K$.
But this means $\alpha^2=a_1^{m_1}\cdots a_{n-1}^{m_{n-1}}a_n\in {K^\times}^2$ which contradicts $\{a_1,...,a_n\}\subset K^\times$ being independent modulo squares since the power of $a_n$ is odd.

Thus $\sqrt{a_n}\not\in L_{n-1}$ and $L_n=L_{n-1}(\sqrt{a_n})$ is a non-trivial quadratic extension with \[\Gal(L_n/L_{n-1})=\langle\sigma_n\rangle\quad\text{where $\;\;\sigma_n(\sqrt{a_n})=-\sqrt{a_n}$.}\] Finally, lifting each of the other $\sigma_i\in\Gal(L_{n-1}/K)$ to $L_n/K$ by letting them act trivially on $\sqrt{a_n}$ gives the result.

Exercise 4.8 Show that the following extensions $L/K$ are Galois. Furthermore, find the Galois group $G=\Gal(L/K)$, the subgroups $H\subset G$ and the corresponding fixed fields $L^H$.

$\;(a)\;$ $L=\mathbb{R}(x)$ over $K=\mathbb{R}(x^2+x^{-2}),$

$\;(b)\;$ $L=\mathbb{R}(x,y)$ over $K=\mathbb{R}(x^2,y^2),$

$\;(c)\;$ $L=\mathbb{R}(x,y)$ over $K=\mathbb{R}(x^2+y^2,xy).$

Solution

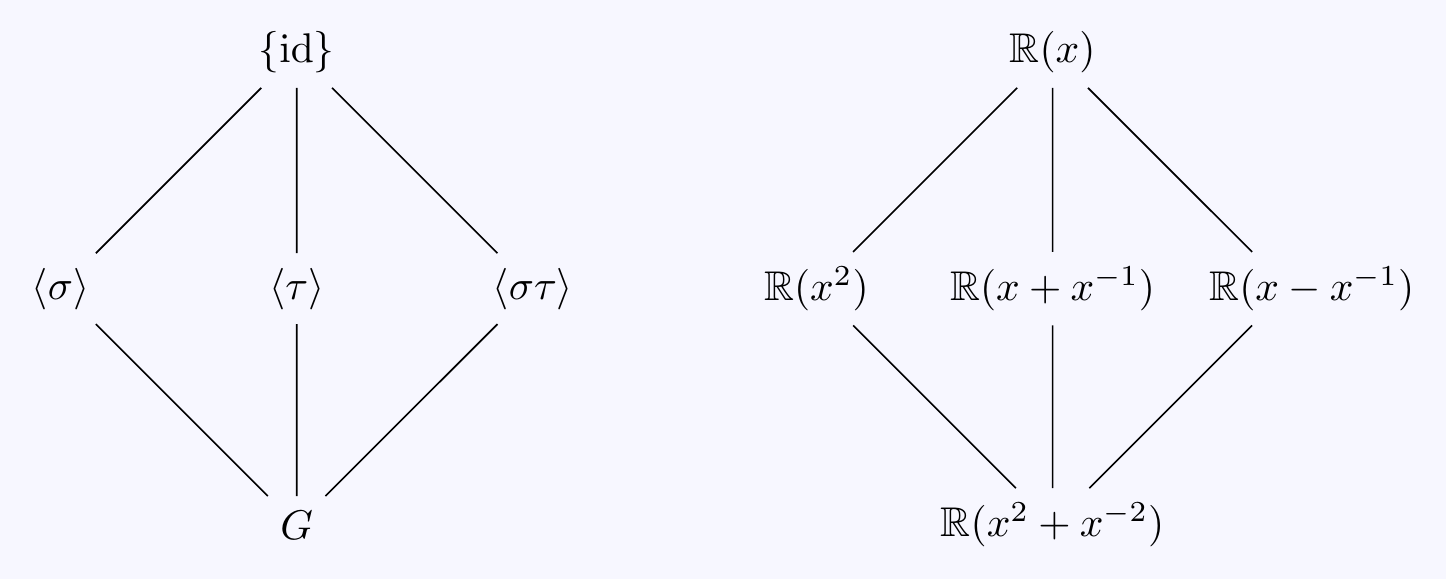
$(a)$ Let $t=x^2+x^{-2}$ so $K=\mathbb{R}(t)$ and $L=K(x)$. Then $x\in L$ is a root of $f(X)=X^4-tX^2+1\in K[X]$ and, in particular, $[L:K]\leq 4$.

Now, we have shown previously (using Gauss’s Lemma) that $f(X)$ is irreducible in $K[X]$, hence is the minimal polynomial of $x$ over $K$ and $[L:K]=4$. However, we now have a more elegant way to see this. Notice that $-x$ is also a root of $f(X)$. Furthermore, so are $\pm x^{-1}$ and so \[f(X)=X^4-tX^2+1=(X-x)(X+x)(X-x^{-1})(X+x^{-1}).\] This means $L=K(x)$ is the splitting field of $f(X)$ over $K$ and so $L/K$ is normal. It is also separable as the characteristic is zero and hence $L/K$ is Galois. We can now define $4$ distinct elements in $G=\Gal(L/K)$ by sending $x$ to the $4$ roots of $f(X)$:

$\id(x)=x$, $\;\sigma(x)=-x$, $\;\tau(x)=x^{-1}\;$ and so $\;\sigma\tau(x)=-x^{-1}$.

Thus we’ve found $[L:K]=|G|\geq 4$ and hence must equal $4$. This implies $f(X)$ is the minimal polynomial of $x$ over $K$ and $[L:K]=4$.

Clearly, $\sigma^2=\tau^2=\id$ and $\sigma\tau=\tau\sigma$ and we now have the structure of the Galois group \[G=\{\id,\sigma,\tau,\sigma\tau\}=\langle\,\sigma,\tau\,\rangle\cong\mathbb{Z}/2\times\mathbb{Z}/2.\] The proper subgroups of $G$ are $\langle\,\sigma\,\rangle$, $\langle\,\tau\,\rangle$, $\langle\,\sigma\tau\,\rangle$ which are each isomorphic to $\mathbb{Z}/2$. For the fixed fields, notice

$\sigma(x^2)=\sigma(x)^2=(-x)^2=x^2$,
$\tau(x+x^{-1})=\tau(x)+\tau(x)^{-1}=x^{-1}+x$,
$\sigma\tau(x-x^{-1})=\sigma(x^{-1}-x)=x-x^{-1}$.

The subgroups and corresponding fixed fields are:

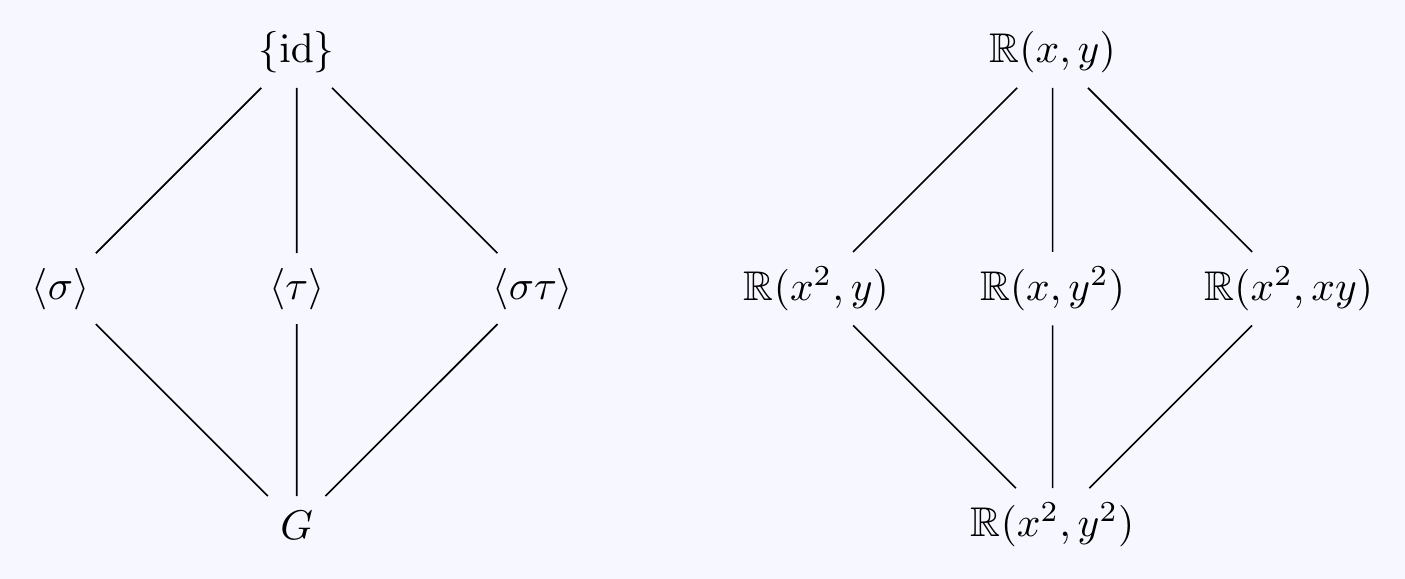
$(b)$ Let $s=x^2$ and $t=y^2$ so $K=\mathbb{R}(s,t)$ and $L=K(\sqrt{s},\sqrt{t})$. Then $\pm x,\pm y$ are roots of the polynomial $f(X)=(X^2-s)(X^2-t)\in K[X]$ and $L$ is the splitting field of $f(X)$ over $K$. We hence have $L/K$ Galois and $[L:K]\leq 4$.

As in part $(a)$, we construct $4$ distinct elements in $G=\Gal(L/K)$ by mapping $x$ and $y$ to roots of $f(X)$:

Define $\sigma,\tau\in\Gal(L/K)$ by $\sigma(x)=-x$, $\sigma(y)=y$ and $\tau(x)=x$, $\tau(y)=-y$.
Note that $\sigma$ and $\tau$ fix $x^2$ and $y^2$ so these are $K$-automorphisms.
We also note that $\sigma\tau(x)=-x$ and $\sigma\tau(y)=-y$ so $\sigma\tau(xy)=xy$.

Now $\sigma^2=\tau^2=\id$ and $\sigma\tau=\tau\sigma$ so once again, the Galois group is \[G=\{\id,\sigma,\tau,\sigma\tau\}=\langle\,\sigma,\tau\,\rangle\cong\mathbb{Z}/2\times\mathbb{Z}/2.\] The subgroups and corresponding fixed fields are as follows:

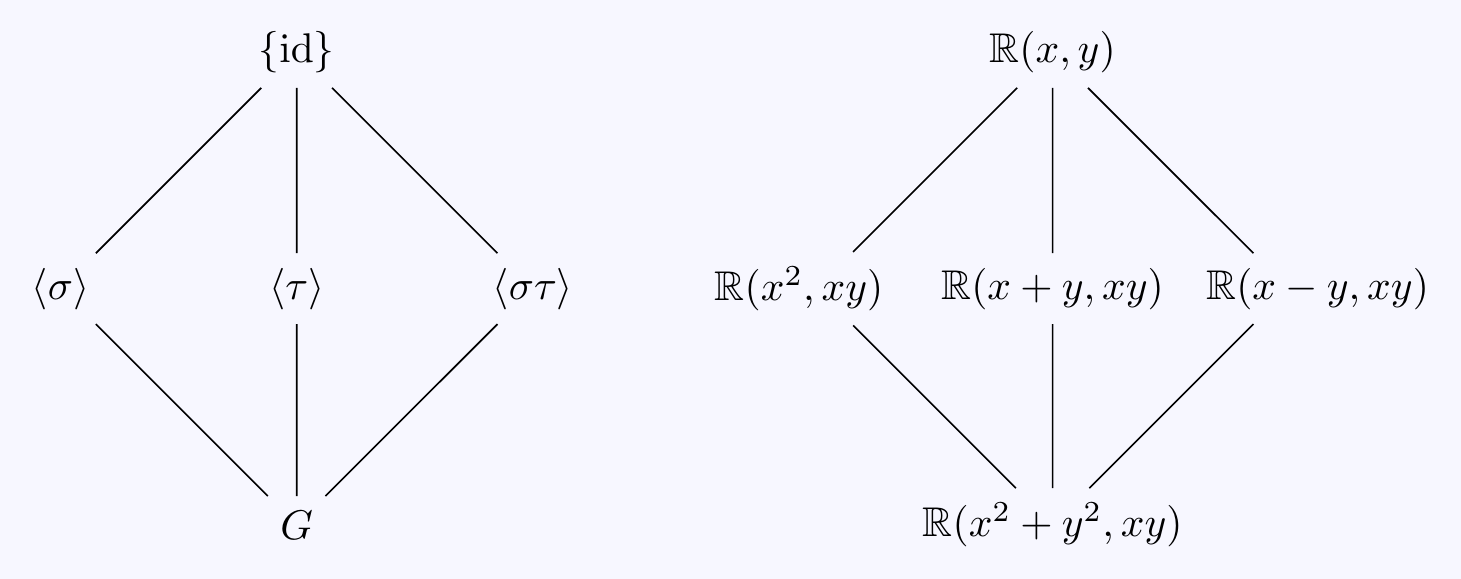
$(c)$ Let $s=x^2+y^2$ and $t=xy$ so $K=\mathbb{R}(s,t)$ and $L=K(x,y)$. Notice that $y=t/x$ so actually, $L=K(x)$. Now $x$ is a root of $f(x)=X^4-sX^2+t^2\in K[X]$ so $[L:K]\leq 4$. Indeed, \[f(X)=(X^2-x^2)(X^2-y^2)=X^4-(x^2+y^2)X^2+x^2y^2=X^4-sX^2+t^2\] and so the four roots are actually $\pm x,\pm y$ and $L$ is the splitting field of $f(X)$ over $K$.

Thus $L/K$ is Galois and we’ll construct $4$ distinct elements in $\Gal(L/K)$ by mapping $x$ and $y$ to roots $\pm x, \pm y$ of $f(X)$. Note that $t=xy\in K$ so these need to fix $xy$ and we can’t take e.g. the choice $\varphi(x)=-x$, $\varphi(y)=y$. Instead,

define $\sigma,\tau\in\Gal(L/K)$ by $\sigma(x)=-x$, $\sigma(y)=-y$ and $\tau(x)=y$, $\tau(y)=x$.
Note that $\sigma$ and $\tau$ fix $x^2+y^2$ and $xy$ so these are $K$-automorphisms. There is also the composition $\sigma\tau\in G$ satisfying $\sigma\tau(x)=-y$ and $\sigma\tau(y)=-x$.

We have $\sigma^2=\tau^2=\id$ and $\sigma\tau=\tau\sigma$ so yet again, we find \[G=\{\id,\sigma,\tau,\sigma\tau\}=\langle\,\sigma,\tau\,\rangle\cong\mathbb{Z}/2\times\mathbb{Z}/2.\] Now find the fixed fields of the order $2$ subgroups $\langle\,\sigma\,\rangle$, $\langle\,\tau\,\rangle$, $\langle\,\sigma\tau\,\rangle$:

We have $\sigma(x^2)=x^2$ and $L^{\langle\,\sigma\,\rangle}=\mathbb{R}(x^2,xy)$.
We have $\tau(x+y)=x+y$ and $L^{\langle\,\tau\,\rangle}=\mathbb{R}(x+y,xy)$. (This is the subfield of symmetric functions in $L$.)
We have $\sigma\tau(x-y)=x-y$ and $L^{\langle\,\sigma\tau\,\rangle}=\mathbb{R}(x-y,xy)$.

Note these are quadratic extensions of $K=\mathbb{R}(x^2+y^2,xy)$ since \[x^2=\sqrt{(x^2+y^2)^2-2(xy)^2}\quad\text{and}\quad x\pm y=\sqrt{(x^2+y^2)\pm2(xy)}.\]

Exercise 4.9 Let $G$ be the group of automorphisms of the field $L=\mathbb{F}_3(x)$ given by \[\sigma_{a,b}:x\mapsto ax+b\quad\text{where $a,b\in\mathbb{F}_3$ and $a\neq 0$.}\] Find all subgroups of $G$ and subfields $M$ with $L^G\subset M\subset L$.

Solution

There are $2$ choices for $a$, $3$ choices for $b$ so $|G|=6$. In particular, $G$ must be isomorphic to either $\mathbb{Z}/2\times\mathbb{Z}/3$ or $S_3\cong D_3$.

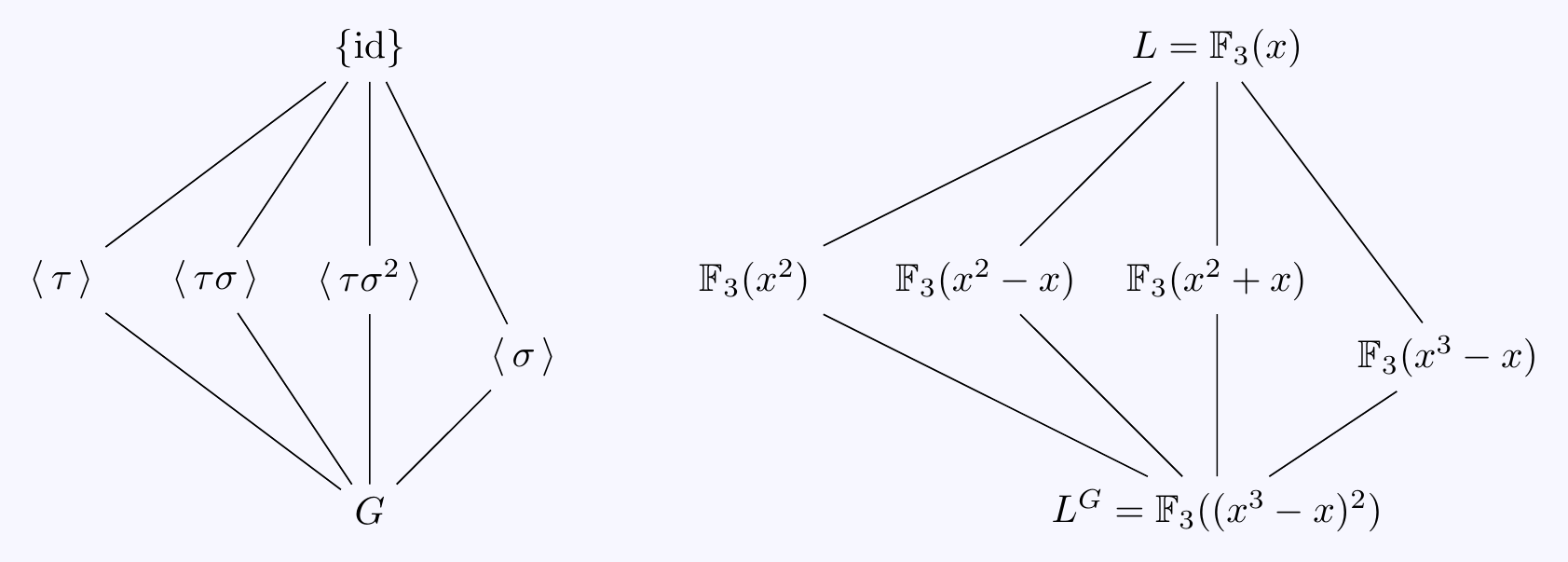
Let $\sigma=\sigma_{1,1}$, i.e. $\sigma(x)=x+1$. This has order $3$ so $G$ has a subgroup \[\langle\,\sigma\,\rangle=\{\id,\sigma,\sigma^2\}\cong\mathbb{Z}/3.\]
Let $\tau=\sigma_{2,0}$, i.e. $\tau(x)=2x=-x$. This has order $2$ so $G$ has a subgroup \[\langle\,\tau\,\rangle=\{\id,\tau\}\cong\mathbb{Z}/2.\]

Notice that $\sigma\tau(x)=\sigma(2x)=2\sigma(x)=2x+2$ and $\tau\sigma^2(x)=\tau(x+2)=2x+2$. Thus we have \[G=\langle\,\sigma, \tau\,\mid\, \sigma^3=\tau^2=\id,\; \tau\sigma\tau=\sigma^{-1}\,\rangle\cong S_3.\]

For the three order $2$ subgroups $\langle\,\tau\,\rangle$, $\langle\,\tau\sigma\,\rangle$, $\langle\,\tau\sigma^2\,\rangle$, the fixed fields will be generated by a quadratic polynomial in $x$ so just see what happens:

$\tau(x^2)=(-x)^2=x^2$.
$\tau\sigma(x)=\tau(x+1)=2x+1$ and $\tau\sigma(x^2)=(2x+1)^2=x^2+x+1$ so $\tau\sigma(x^2-x)=x^2-x$.
$\tau\sigma^2(x)=\tau(x+2)=2x+2$ and $\tau\sigma^2(x^2)=(2x+2)^2=x^2+2x+1$ so $\tau\sigma(x^2+x)=x^2+x$.

Thus we have found fixed fields \[L^{\langle\,\tau\,\rangle}=\mathbb{F}_3(x^2),\qquad L^{\langle\,\tau\sigma\,\rangle}=\mathbb{F}_3(x^2-x),\qquad L^{\langle\,\tau\sigma^2\,\rangle}=\mathbb{F}_3(x^2+x).\]

There is one order $3$ subgroup $\langle\,\sigma\,\rangle$. Now $\sigma(x^3)=(x+1)^3=x^3+1$ so $\sigma(x^3-x)=x^3-x$ and \[L^{\langle\,\sigma\,\rangle}=\mathbb{F}_3(x^3-x).\] Finally, we need to find $L^G$. Notice how $\tau$ operates on $x^3-x$: we have $\tau(x^3-x)=-(x^3-x)$ so $\tau((x^3-x)^2)=(x^3-x)^2$ and \[L^G=\mathbb{F}_3((x^3-x)^2)=\mathbb{F}_3(x^6+x^4+x^2).\]

4 Problem Sheet 4: Computations with Galois groups

4 Problem Sheet 4:
Computations with Galois groups