3 Problem Sheet 3:
Properties of field extensions

Exercise 3.1 Find a basis of the splitting field $L$ of $f(x)$ over $K$ in the following cases:

$\;(a)\;\;f(x)=(x^2-2)(x^2-5)$ over $K=\mathbb{Q},\hspace{2em}$ $\;(b)\;\;f(x)=x^4+1$ over $K=\mathbb{Q},$

$\;(c)\;\;f(x)=x^8-2$ over $K=\mathbb{Q},\hspace{6.15em}$ $\;(d)(\star)\;\;f(x)=x^4+x^2-1$ over $K=\mathbb{Q},$

$\;(e)\;\;f(x)=x^6-2$ over $K=\mathbb{Q}(\sqrt{-3}),\hspace{3.15em}$ $\;(f)\;\;f(x)=x^8-2$ over $K=\mathbb{Q}(i).$

Solution

$(a)\;$ We need the roots $\pm\sqrt{2},\pm\sqrt{5}$ in the splitting field $L$ so $L=\mathbb{Q}(\sqrt{2},\sqrt{5})$. Notice $\sqrt{10}=\sqrt{2}\sqrt{5}\in L$ as well and a $\mathbb{Q}$-basis is $\{1,\sqrt{2},\sqrt{5},\sqrt{10}\}$. Explicitly, the polynomial splits in $L$ as \[(x^2-2)(x^2-5)=(x+\sqrt{2})(x-\sqrt{2})(x+\sqrt{5})(x-\sqrt{5})\] and $L=\left\{a+b\sqrt{2}+c\sqrt{5}+d\sqrt{10} \;\mid\; a,b,c,d\in\mathbb{Q}\right\}$.

$(b)\;$ Let $\zeta=e^{\pi i/4}$. Then $\zeta^2=i$ and the four (distinct) roots are $\zeta$, $-\zeta=\zeta^5$, $i\zeta=\zeta^3$ and $-i\zeta=\zeta^7$ \[x^4+1=(x-\zeta)(x-\zeta^3)(x-\zeta^5)(x-\zeta^7).\] We have $L=\mathbb{Q}(\zeta)$ and a $\mathbb{Q}$-basis is $\{1,\zeta,i,i\zeta\}=\{1,\zeta,\zeta^2,\zeta^3\}$.

Alternatively, since $\zeta=(1+i)/\sqrt{2}$, we can write $L=\mathbb{Q}(i,\sqrt{2})$ and give another basis $\{1,i,\sqrt{2},i\sqrt{2}\}$.

$(c)\;$ The splitting field contains the real root $\theta=\sqrt[8]{2}$. The eight roots are then $\zeta^j\theta$ for $0\leq j\leq 7$ where \[\zeta=e^{\pi i/4}=(1+i)/\sqrt{2}=(1+i)/\theta^4.\] Thus $L=\mathbb{Q}(\theta,\zeta)=\mathbb{Q}(\theta,i)$ and a $\mathbb{Q}$-basis is $\{1,\theta,...,\theta^7,i,i\theta,...,i\theta^7\}$. There are other ways to write down a basis, but it must have $[L:\mathbb{Q}]=16$ linearly independent elements.

$(d)\;$ Notice that $x^4+x^2-1=(x^2-\alpha)(x^2-\beta)$ where $\begin{cases} \alpha=(-1+\sqrt{5})/2, \\ \beta=(-1-\sqrt{5})/2.\end{cases}$.

The splitting field contains $\pm\sqrt{\alpha},\pm\sqrt{\beta}$ and so $L=\mathbb{Q}(\sqrt{\alpha},\sqrt{\beta})$. However, it’s not immediately obvious what $[L:\mathbb{Q}]$ is, and we certainly need to know it since it is the dimension of a basis.

One way is to consider the degrees in the diagram

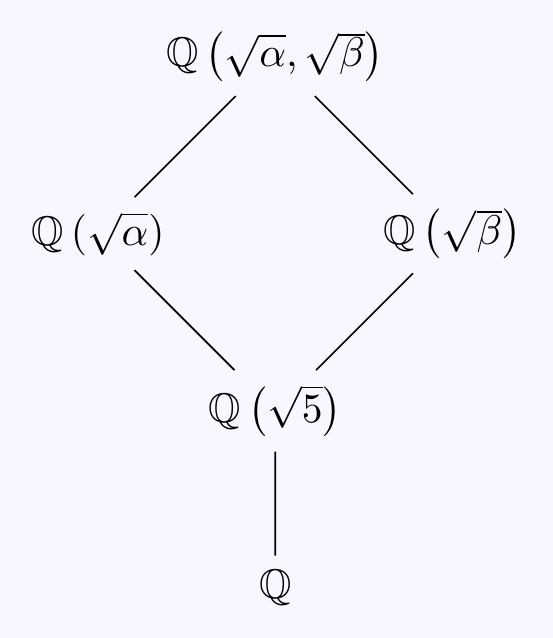
Notice $\beta\in\mathbb{Q}(\beta)=\mathbb{Q}(\sqrt{5})$ but $\beta$ is a negative real number. This means that $\sqrt{\beta}\not\in\mathbb{Q}(\sqrt{5})$ and so $[\mathbb{Q}(\sqrt{\beta}):\mathbb{Q}(\sqrt{5}]=2$. By the Tower Law, \[ [\mathbb{Q}(\sqrt{\beta}):\mathbb{Q}]=[\mathbb{Q}(\sqrt{\beta}):\mathbb{Q}(\sqrt{5})] [\mathbb{Q}(\sqrt{5}):\mathbb{Q}]=4.\]
This implies $x^4+x^2-1\in\mathbb{Q}[x]$ is irreducible (alternatively, this could be shown directly.)
Now $\sqrt{\alpha},\sqrt{\beta}$ are roots of the same irreducible polynomial so $[\mathbb{Q}(\sqrt{\alpha}):\mathbb{Q}]=[\mathbb{Q}(\sqrt{\beta}):\mathbb{Q}]=4$.
Finally, $\mathbb{Q}(\sqrt{\alpha})$ is real so adjoining $\sqrt{\beta}\not\in\mathbb{Q}(\sqrt{\alpha})$ gives $[\mathbb{Q}(\sqrt{\alpha},\sqrt{\beta}):\mathbb{Q}(\sqrt{\alpha})]=2$.
Hence $[\mathbb{Q}(\sqrt{\alpha},\sqrt{\beta}):\mathbb{Q}]=8$ and a $\mathbb{Q}$-basis is \[\left\{1,\sqrt{5},\sqrt{\alpha},\sqrt{5\alpha},\sqrt{\beta},\sqrt{5\beta},\sqrt{\alpha\beta},\sqrt{5\alpha\beta}\right\}.\]
Using $\alpha\beta=-1$, we actually have $\sqrt{\beta}=i/\sqrt{\alpha}$ and we could re-write to get a basis \[\left\{1,i,\sqrt{5},i\sqrt{5},\sqrt{\alpha},i\sqrt{\alpha},\sqrt{5\alpha},i\sqrt{5\alpha}\right\}.\] Notice another way of writing the splitting field is $L=\mathbb{Q}(i,\sqrt{5},\sqrt{\alpha})$.

$(e)\;$ The 6 roots are $\zeta^j\sqrt[6]{2}$ for $0\leq j\leq 5$ where $\zeta=e^{\pi i/3}$ so the splitting field is $L=K(\zeta,\sqrt[6]{2})$.

We have $\zeta=(1+\sqrt{-3})/2$ which is in $K=\mathbb{Q}(\sqrt{-3})$ so actually $L=K(\sqrt[6]{2})$.
To check the degree of $L/K$, notice $\sqrt{-3}$ is not real so $\sqrt{-3}\not\in\mathbb{Q}(\sqrt[6]{2})$. Hence \[[L:\mathbb{Q}]=[L:\mathbb{Q}(\sqrt[6]{2})] [\mathbb{Q}(\sqrt[6]{2}):\mathbb{Q}]=12\] and so $[L:K]=6$. A $K$-basis is $\left\{1,\theta,\theta^2,\theta^3,\theta^4,\theta^5\right\}$ where $\theta=\sqrt[6]{2}$.

$(f)\;$ In a similar way, the roots are $\zeta^j\theta$ for $0\leq j\leq 7$ where $\theta=\sqrt[8]{2}$ and \[\zeta=e^{\pi i/4}=(1+i)/\sqrt{2}=(1+i)/\theta^4.\]

We find $L=\mathbb{Q}(i,\theta)=K(\theta)$, $[L:K]=8$ and a $K$-basis of $L$ is $\left\{1,\theta,...,\theta^7\right\}$.

Exercise 3.2 Let $\theta$ be a root of the polynomial $f(x)=x^3+x+1\in\mathbb{F}_2[x]$. Show that the extension $\mathbb{F}_2(\theta)$ is a splitting field for $f(x)$ over $\mathbb{F}_2$.

Solution

Given that $f(\theta)=\theta^3+\theta+1=0$, we have \[f(\theta^2)=\theta^6+\theta^2+1=(\theta^3+\theta+1)^2=f(\theta)^2=0\] and similarly, $f(\theta^4)=f(\theta)^4=0$. Thus the three distinct roots $\theta$, $\theta^2$ and $\theta^4=\theta+\theta^2$ are contained in $\mathbb{F}_2(\theta)$ and this is the splitting field of $f(x)$ over $\mathbb{F}_2$.

Exercise 3.3 Let $p$ be a prime number. What is the degree of the splitting field of $x^p-1$ over $\mathbb{Q}$?

Solution

Let $\zeta=e^{2\pi i/p}$. Then the roots of $x^p-1$ are $1,\zeta,...,\zeta^{p-1}$ and $\mathbb{Q}(\zeta)$ is the splitting field of $x^p-1$ over $\mathbb{Q}$. Furthermore, $\zeta$ is a root of \[g(x)=\frac{x^p-1}{x-1}=x^{p-1}+x^{p-2}+\cdots+x+1\] which is irreducible over $\mathbb{Q}$ (by applying Eisenstein’s Criterion to $g(x+1)$). Hence the splitting field has degree $[\mathbb{Q}(\zeta):\mathbb{Q}]=\deg(g(x))=p-1$.

Exercise 3.4 Decide whether or not the following pairs of fields are isomorphic:

$\;(a)\;\;\mathbb{Q}(\sqrt[4]{2})$ and $\mathbb{Q}(i\sqrt[4]{2}),\hspace{5em}$ $\;(b)\;\;\mathbb{Q}(\sqrt[3]{1+\sqrt{3}})$ and $\mathbb{Q}(\sqrt[3]{1-\sqrt{3}}),$

$\;(c)\;\;\mathbb{Q}(\sqrt{2})$ and $\mathbb{Q}(\sqrt{3}),\hspace{5.4em}$ $\;(d)\;\;\mathbb{Q}(\pi)$ and $\mathbb{Q}(e)$.

Solution

$(a)$ Yes, since $\sqrt[4]{2}$ and $i\sqrt[4]{2}$ are roots of the same irreducible polynomial $x^4-2\in\mathbb{Q}[x]$.

Note, we are not saying that $\mathbb{Q}(\sqrt[4]{2})$ and $\mathbb{Q}(i\sqrt[4]{2})$ the same subfield of $\mathbb{C}$, and indeed they aren’t - the first one only contains real numbers. However, recall the universal property of simple extensions - it tells us that the two given extensions are both isomorphic to $\mathbb{Q}[x]/(x^4-2)$ as fields and this only depends on the minimal polynomial $x^4-2$.

$(b)$ Again yes, since $\sqrt[3]{1+\sqrt{3}}$ and $\sqrt[3]{1-\sqrt{3}}$ have the same minimal polynomial, namely \[x^6-2x^3-2\in\mathbb{Q}[x]\] (which is irreducible by applying Eisenstein’s Criterion with $p=2$).

$(c)$ No. Suppose that $\sigma:\mathbb{Q}(\sqrt{2})\to\mathbb{Q}(\sqrt{3})$ is an isomorphism. Then $\sigma(\sqrt{2})=a+b\sqrt{3}$ for some $a,b\in\mathbb{Q}$ and \[(a+b\sqrt{3})^2=\sigma(\sqrt{2})^2=\sigma(2)=2 \quad\implies\begin{cases} a^2+3b^2=2 \\ \;\;\;\;\;\;\;2ab=0 \end{cases}\] No such $a,b\in\mathbb{Q}$ exist since $a=0$ implies $\sqrt{2/3}\in\mathbb{Q}$ and $b=0$ implies $\sqrt{2}\in\mathbb{Q}$. Hence there is no such isomorphism.

$(d)$ Yes. Both fields are isomorphic to the field of rational expressions $\mathbb{Q}(t)$ as in Proposition 3.2. Composing these gives an isomorphism \[\begin{align*} \varphi\;:\; \mathbb{Q}(\pi) &\longrightarrow \,\mathbb{Q}(e) \\ \frac{f(\pi)}{g(\pi)} &\longmapsto \frac{f(e)}{g(e)} \qquad\text{for $f(t),g(t)\in K[t]$ with $g(t)\neq 0$} \end{align*}\]

Again, we are not saying they are the same subfield of $\mathbb{R}$. In fact, if you can answer that question, let me know as it is an open problem. It’s not even known if $\pi+e$ is rational or not.

Exercise 3.5 Describe the splitting field of $x^3-11$ over $\mathbb{Q}$. Show that if $\alpha$ is any root of this polynomial then $\mathbb{Q}(\alpha)/\mathbb{Q}$ is not normal.

Solution

Let $\omega=e^{2\pi i/3}=(-1+\sqrt{-3})/2$, then the three roots are $\alpha$, $\omega\alpha$ and $\omega^2\alpha$ and \[x^3-11=(x-\alpha)(x-\omega\alpha)(x-\omega^2\alpha).\] The splitting field is \[L=\mathbb{Q}(\alpha,\omega\alpha,\omega^2\alpha)=\mathbb{Q}(\alpha,\omega)=\mathbb{Q}\left(\alpha,\sqrt{-3}\,\right).\] To fully describe this extension we should also show it has degree $[L:\mathbb{Q}]=6$, which we can do by applying the Tower Law to the diagram

$\mathbb{Q}(\alpha)\subset L$ so $[\mathbb{Q}(\alpha):\mathbb{Q}]=3$ divides $[L:\mathbb{Q}]$ and $\mathbb{Q}(\omega)\subset L$ so $[\mathbb{Q}(\omega):\mathbb{Q}]=2$ divides $[L:\mathbb{Q}]$. Hence we have $[L:\mathbb{Q}]\geq 6$.
However, $[\mathbb{Q}(\omega)(\alpha):\mathbb{Q}(\omega)]\leq 3$ so $[L:\mathbb{Q}]=[\mathbb{Q}(\omega)(\alpha):\mathbb{Q}(\omega)] [\mathbb{Q}(\omega):\mathbb{Q}]\leq 3\cdot 2=6$.
Note we didn’t know that $x^3-11$ was irreducible in $\mathbb{Q}(\omega)[x]$. However, now we know it is since the above implies $[\mathbb{Q}(\omega)(\alpha):\mathbb{Q}(\omega)]=3$

To show that $\mathbb{Q}(\alpha)/\mathbb{Q}$ is not normal:

If it was, then all three roots $\alpha$, $\omega\alpha$, $\omega^2\alpha$ are in $\mathbb{Q}(\alpha)$.
Then $(\omega\alpha)/\alpha=\omega\in\mathbb{Q}(\alpha)$ so $\mathbb{Q}\subset\mathbb{Q}(\omega)\subset\mathbb{Q}(\alpha)$.
But that would imply $[\mathbb{Q}(\omega):\mathbb{Q}]=2$ divides $[\mathbb{Q}(\alpha):\mathbb{Q}]=3$, so we have a contradiction.

Exercise 3.6 Suppose that $K\subset M\subset L$ is a tower of finite extensions. For each of the following, either prove the statement or provide a counterexample.

$\;(a)\;$ If $L/M$ and $M/K$ are both normal, then $L/K$ is normal.

$\;(b)\;$ If $L/K$ is normal, then $M/K$ is normal.

$\;(c)\;$ If $L/K$ is normal, then $L/M$ is normal.

Solution

$(a)$ This is false. Consider the tower \[ K=\mathbb{Q} \;\;\;\subset\;\;\; M=\mathbb{Q}(\sqrt{2}) \;\;\;\subset\;\;\; L=\mathbb{Q}(\sqrt[4]{2}).\] Then $L/M$ and $M/K$ are quadratic extensions so automatically normal. However, the polynomial $x^4-2\in\mathbb{Q}[x]$ is irreducible over $\mathbb{Q}$ (for instance, by Eisenstein’s criterion with $p=2$). This polynomial has two roots $\pm\sqrt[4]{2}$ in $L$ but the other two roots $\pm i\sqrt[4]{2}$ are not in $L$. This means $L/K$ is not normal.

$(b)$ This is also false. Consider the tower \[ K=\mathbb{Q} \;\;\;\subset\;\;\; M=\mathbb{Q}(\sqrt[3]{2}) \;\;\;\subset\;\;\; L=\mathbb{Q}(\sqrt[3]{2},\omega)\] where $\omega=e^{2\pi i/3}$. Then $L/K$ is normal as it is the splitting field of $f(x)=x^3-2$ over $\mathbb{Q}$. Now $f(x)$ is irreducible over $\mathbb{Q}$ (by Eisenstein again or because it is a cubic with no roots in $\mathbb{Q}$). But $f(x)$ has one root $\sqrt[3]{2}\in M$ but the other two roots are not real so not in $M$, and hence $M/K$ is not normal.

$(c)$ This is true. If $L/K$ is normal, then it is the splitting field of some polynomial $f(x)\in K[x]$ over $K$ and there are $\theta_1,...,\theta_n\in L$ with

$f(x)=c(x-\theta_1)\cdots(x-\theta_n)$,
$L=K(\theta_1,...,\theta_n)$.

Clearly, $f(x)\in M[x]$, $f(x)$ splits completely in $L[x]$ and $L=M(\theta_1,...,\theta_n)$. Hence $L$ is the splitting field of $f(x)$ over $M$ and $L/M$ is normal.

Alternatively: suppose $\alpha\in L$ has minimal polynomial $m_K(x)$ over $K$ and minimal polynomial $m_M(x)$ over $M$. Recall that $m_M(x)$ generates the ideal of all polynomials in $M[x]$ which vanish at $\alpha$. Since $m_K(x)\in K[x]\subset M[x]$ and $m_K(\alpha)=0$, this means that $m_M(x)$ divides $m_K(x)$ in $M[x]$. Now $L/K$ being normal implies that $m_K(x)$ splits into linear factors in $L[x]$. Hence $m_M(x)$ does as well and so $L/M$ is normal.

Exercise 3.7 Are the following true or false? Justify your answers.

$\;(a)\;$ A degree $2$ extension $L/K$ is normal.

$\;(b)\;$ A degree $2$ extension $L/K$ is separable.

Solution

$(a)$ Yes. This was shown in lectures as follows: suppose $\theta\in L$ has minimal polynomial $m(x)\in K[x]$. Then $K\subset K(\theta)\subset L$ and so $\deg(m(x))=[K(\theta):K]=1$ or $2$.

If $\deg(m(x))=1$, then there is nothing to prove, as $m(x)$ is already linear.
If $\deg(m(x))=2$, then $m(x)=(x-\theta)m_1(x)$ where $m_1(x)\in L[x]$ is linear. Thus $m(x)$ splits completely in $L[x]$.

$(b)$ No. Consider the field of rational expressions $K=\mathbb{F}_2(t)$ and the quadratic extension $L=K(\theta)$ where $\theta^2=t$. Then $L/K$ is not separable as the element $\theta\in L$ isn’t separable - its minimal polynomial \[x^2-t=x^2-\theta^2=(x-\theta)^2\] has a repeated root.

Exercise 3.8 Suppose $K\subset M\subset L$ be a tower of finite extensions.

$(a)$ Show that if $L/K$ is separable, then both $L/M$ and $M/K$ are separable.

$(b)(\star)$ Show that if $L/M$ and $M/K$ are separable, then $L/K$ is separable.

(For $(b)$, you may use the following characterisation of separable extensions in characteristic $p$: A finite extension $L/K$ is separable if and only if $L=KL^p$, i.e. any $\alpha\in L$ can be written as $\alpha=c\beta^p$ where $c\in K$ and $\beta\in L$.)

Solution

$(a)$ To show $L/K$ separable $\Rightarrow L/M$ separable:

Given $\alpha\in L$, the minimal polynomial $m_K(x)\in K[x]$ of $\alpha$ over $K$ has no repeated roots.
Let $m_M(x)\in M[x]$ be the minimal polynomial of $\alpha$ over $M$. Then $m_K(x)\in M[x]$ and $m_K(\alpha)=0$ so $m_M(x)$ divides $m_K(x)$ in $M[x]$.
Hence $m_M(x)$ has no repeated roots and $L/M$ is separable.

To show $L/K$ separable $\Rightarrow M/K$ separable is almost trivial:

Any $\beta\in M$ is also in $L$, hence its minimal polynomial over $K$ has no repeated roots.

$(b)$ If $\ch(K)=0$ then we already know any finite extension of $K$ is separable. Hence we can restrict to the characteristic $p$ case and use the stated characterisation.

If $L/M$ and $M/K$ are separable, then $L=ML^p$ and $M=KM^p$
Thus $L=ML^p=KM^pL^p\subset KL^p\subset L.$
We must have equality throughout and so $L=KL^p$ which implies $L/K$ is separable.

There are multiple ways to answer $(b)$, however, they are all quite hard or require things we haven’t covered. The stated characterisation can be proved in a similar way to Theorem 4.8 in the notes, but is a little more involved. See Brzezinski’s book (Exercise 8.3) for more details.

Exercise 3.9 Which of the following field extensions $L/K$ are normal? Justify your answers.

$\;(a)\;$ $L=\mathbb{Q}(\sqrt[4]{2})$ over $K=\mathbb{Q},\hspace{5em}$ $\;(b)\;$ $L=K(\sqrt[6]{2})$ over $K=\mathbb{Q}(\sqrt{-3}),$

$\;(c)\;$ $L=K(\sqrt[4]{2},\sqrt[4]{3})$ over $K=\mathbb{Q}(i),\hspace{2.05em}$ $\;(d)\;$ $L=\mathbb{C}$ over $K=\mathbb{R},$

$\;(e)\;$ $L=\mathbb{Q}(\sqrt[8]{2},i)$ over $K=\mathbb{Q},\hspace{4.05em}$ $\;(f)\;$ $L=\mathbb{Q}(\sqrt[14]{2})$ over $K=\mathbb{Q}(\sqrt[7]{2}),$

$\;(g)\;$ $L=\mathbb{Q}(\sqrt[4]{2},i)$ over $K=\mathbb{Q},\hspace{4.05em}$ $\;(h)\;$ $L=\mathbb{Q}(x)$ over $K=\mathbb{Q}(x^3),$

$\;(i)\;$ $L=\mathbb{C}(x)$ over $K=\mathbb{C}(x^5),\hspace{4.15em}$ $\;(j)\;$ $L=\mathbb{F}_5(x)$ over $K=\mathbb{F}_5(x^4).$

Solution

Typical method: show that $L$ is the splitting field of some polynomial $f(x)$ over $K$ or show that the minimal polynomial of some element in $L$ doesn’t split completely in $L[x]$.

$(a)$ This extension is not normal. The element $\sqrt[4]{2}\in L$ has minimal polynomial $f(x)=x^4-2$ over $\mathbb{Q}$ which is irreducible over $\mathbb{Q}$ by e.g. the Rational Root test. But $L\subset\mathbb{R}$ so $L$ doesn’t contain the non-real roots of $f(x)$, e.g. $i\sqrt[4]{2}$.

$(b)$ This extension is normal as $L=K\left(\sqrt[6]{2}\right)$ is the splitting field of $f(x)=x^6-2$ over $K=\mathbb{Q}\left(\sqrt{-3}\right)$. Indeed, the roots of $f(x)$ are $\zeta^{j}\sqrt[6]{2}\in L$ for $0\leq j\leq 5$ where $\zeta=e^{\pi i/3}=(1+\sqrt{-3})/2$. Hence \[L=\mathbb{Q}\left(\sqrt[6]{2},\zeta\sqrt[6]{2},...,\zeta^5\sqrt[6]{2}\right)=\mathbb{Q}(\zeta,\sqrt[6]{2})=\mathbb{Q}(\sqrt{-3},\sqrt[6]{2})=K(\sqrt[6]{2})\] is the splitting field of $f(x)$ over $K$.

$(c)$ This extension is normal as $L=K\left(\sqrt[4]{2},\sqrt[4]{3}\right)$ is the splitting field of $f(x)=(x^4-2)(x^4-3)$ over $K=\mathbb{Q}(i)$. The roots of $f(x)$ are $\pm\sqrt[4]{2},\,\pm i\sqrt[4]{2},\, \pm\sqrt[4]{3},\, \pm i\sqrt[4]{3}\in L$ and \[L=\mathbb{Q}\left(i,\sqrt[4]{2},\sqrt[4]{3}\right)=K\left(\sqrt[4]{2},\sqrt[4]{3}\right).\]

$(d)$ The extension $\mathbb{C}/\mathbb{R}$ is normal as it has degree $2$. (Alternatively, notice $\mathbb{C}=\mathbb{R}(i)$ is the splitting field of $x^2+1$ over $\mathbb{R}$.)

$(e)$ This extension is normal as $L=K\left(\sqrt[8]{2},i\right)$ is the splitting field of $f(x)=x^8-2$ over $K=\mathbb{Q}$. The roots of $f(x)$ are $\zeta^{j}\sqrt[8]{2}\in L$ for $0\leq j\leq 7$ where \[\zeta=e^{\pi i/4}=(1+i)/\sqrt{2}\in\mathbb{Q}(i,\sqrt{2})\subset L\]

$(f)$ This extension is normal as it has degree $2$ - the element $\sqrt[14]{2}$ is a root of $x^2-\sqrt[7]{2}\in K[x]$.

$(g)$ This extension is normal as $L=\mathbb{Q}(i,\sqrt[4]{2})$ is the splitting field of $f(x)=x^4-2$ over $K=\mathbb{Q}$. The roots of $f(x)$ are $\pm\sqrt[4]{2},\pm i\sqrt[4]{2}\in L$ and these roots clearly generate $L$.

$(h)$ This extension is not normal. Let $t=x^3$ so that $K=\mathbb{Q}(t)$ and $L=K(x)$. The minimal polynomial of $x$ over $K$ is \[f(X)=X^3-t\in K[X]=\mathbb{Q}(t)[X].\] This is irreducible over $K$, e.g. by the generalised Eisenstein’s criterion with $p=t$. Also, the roots of $f(X)$ are $x$, $\omega x$, $\omega^2x$ where $\omega=e^{2\pi i/3}$. If $L/K$ was normal, then these would all be in $L$ and so $\omega=(\omega x)/x\in L=\mathbb{Q}(x)$. Now recall Example $3.2(d)$ from the lecture notes: any element of $\mathbb{Q}(x)$ which is algebraic over $\mathbb{Q}$ must be in $\mathbb{Q}$. But $\omega^3-1=0$ so $\omega$ is algebraic over $\mathbb{Q}$. We thus must have $\omega\in\mathbb{Q}$ which is false ($\omega$ isn’t real, never mind rational…)

$(i)$ This extension is normal. Let $t=x^5$ so that $K=\mathbb{C}(t)$, $L=K(x)$ and $x$ is a root of $f(X)=X^5-t\in K[X]=\mathbb{C}(t)[X].$ This polynomial splits completely in $L[X]$: \[f(X)=X^5-t=(X-x)\left(X-\zeta x\right)\left(X-\zeta^2x\right)\left(X-\zeta^3x\right)\left(X-\zeta^4x\right)\] where $\zeta=e^{2\pi i/5}\in\mathbb{C}$. Thus $L=K(\zeta,x)=K(x)$ is the splitting field of $f(x)$ over $K$.

$(j)$ This extension is normal. Let $t=x^4$ so that $K=\mathbb{F}_5(t)$ and $L=K(x)$. The minimal polynomial of $x$ over $K$ is $f(X)=X^4-t\in K[X]=\mathbb{F}_5(t)[X]$ and this polynomial splits completely in $L[X]$: \[\begin{align*} f(X)=X^4-t=X^4-x^4&=(X^2-x^2)(X^2+x^2) \\ &=(X-x)(X+x)(X-2x)(X+2x) \end{align*}\] (Notice that $\pm1, \pm2$ are the four distinct $4\,$th roots of $1$ in $\mathbb{F}_5$.) Thus $L=K(x)$ is the splitting field of $f(x)$ over $K$.

Exercise 3.10 Find a normal closure $N$ for the following extensions $L/K$.

$\;(a)\;$ $L=\mathbb{Q}(\sqrt[4]{2})$ over $K=\mathbb{Q},\hspace{4em}$ $\;(b)\;$ $L=\mathbb{Q}(\sqrt[6]{2},\sqrt{-3})$ over $K=\mathbb{Q}(\sqrt{-3}),$

$\;(c)\;$ $L=\mathbb{Q}(e^{2\pi i/5})$ over $K=\mathbb{Q},\hspace{3.1em}$ $\;(d)\;$ $L=\mathbb{Q}(x)$ over $K=\mathbb{Q}(x^3),$

$\;(e)\;$ $L=\mathbb{Q}(x)$ over $K=\mathbb{Q}(x^4),\hspace{2.95em}$ $\;(f)\;$ $L=\mathbb{F}_3(x)$ over $K=\mathbb{F}_3(x^4),$

$\;(g)\;$ $L=\mathbb{F}_2(x)$ over $K=\mathbb{F}_2(x^4).$

Solution

$(a)$ The normal closure is $N=\mathbb{Q}(\sqrt[4]{2},i)$. Indeed, the minimal polynomial of $\sqrt[4]{2}$ over $\mathbb{Q}$ is $x^4-2$ and this has roots $\pm\sqrt[4]{2}, \pm i\sqrt[4]{2}$. In particular, $L/K$ is not normal but we just need to adjoin $i$ to $L$ to get a normal extension $N/K$.

$(b)$ We have $L=K(\sqrt[6]{2})$ and $\zeta=e^{\pi i/3}=(1+\sqrt{-3})/2\in K$. The six roots of $x^6-2$ are all in $L$ since they are just $\zeta^j\sqrt[6]{2}$ for $0\leq j\leq 5$. In particular, $L$ is the splitting field of this polynomial over $K$, so $L/K$ is already normal and $N=L$.

$(c)$ Again, the normal closure is just $N=L$ since $L$ is already normal over $\mathbb{Q}$. It is the splitting field of $x^5-1$ over $\mathbb{Q}$, which has roots $1,\zeta,\zeta^2,\zeta^3,\zeta^4$ where $\zeta=e^{2\pi i/5}\in L$.

$(d)$ Since $x\in L$ is a root of $X^3-x^3\in K[X]$, we need the cube roots of unity to get all the roots \[X^3-x^3=(X-x)(X-\omega x)(X-\omega^2 x) \quad\text{where $\omega=e^{2\pi i/3}$}.\] This means $N=\mathbb{Q}(\omega,x)$, which is the splitting field of this polynomial over $K=\mathbb{Q}(x^3)$.

$(e)$ Similarly, we now need the fourth roots of unity to get all the roots \[X^4-x^4=(X-x)(X+x)(X-ix)(X+ix)\] and $N=\mathbb{Q}(i,x)$ is the splitting field of this polynomial over $K=\mathbb{Q}(x^4)$.

$(f)$ Likewise, we need fourth roots of unity, but this time we can’t directly use $i\in\mathbb{C}$. Instead, let $\alpha$ be a root of $X^2+1\in\mathbb{F}_3[X]$. Then there are four 4-th roots of unity $\pm 1,\pm\alpha$ contained in $\mathbb{F}_3(\alpha)=\mathbb{F}_9$. In particular, $N=\mathbb{F}_3(\alpha,x)=\mathbb{F}_9(x)$.

$(g)$ Finally, $N=L$ since $L/K$ is already normal - it is the splitting field of $X^4-x^4\in K[X]$ because $X^4-x^4=(X-x)^4$, i.e. $x$ is the only root of of this polynomial. Note the extension is not separable as the root has multiplicity $4$.

Exercise 3.11 Suppose that $\alpha, \beta$ are algebraic over a field $K$ and furthermore, $K(\alpha)/K$ is normal and $K(\alpha)\cap K(\beta)=K$. Show that \[[K(\alpha,\beta):K]=[K(\alpha):K)] [K(\beta):K].\]

Solution

In Section 3.5 of the notes, we showed that for $\alpha,\beta$ algebraic over $K$, we have an inequality \[ [K(\alpha,\beta):K]\leq [K(\alpha):K] [K(\beta):K].\] We have to show that the extra conditions $K(\alpha)/K$ normal and $K(\alpha)\cap K(\beta)=K$ imply this is actually an equality. In particular, a proof must use both of these conditions.

If $\alpha\in K$, then there is nothing to prove, so suppose $\alpha\not\in K$ and let $f(x)\in K[x]$ be its minimal polynomial over $K$. We will show the given conditions imply $f(x)$ is irreducible over $K(\beta)$ and so $f(x)$ is actually the minimal polynomial of $\alpha$ over $K(\beta)$:

As $K(\alpha)/K$ is normal, $f(x)$ splits completely \[f(x)=(x-\alpha_1)(x-\alpha_2)\cdots(x-\alpha_n)\in K(\alpha)[x]\] and so any factor of $f(x)$ has coefficients in $K(\alpha)$.
Any factor of $f(x)$ in $K(\beta)[x]$ also has coefficients in $K(\beta)$, and hence in $K(\alpha)\cap K(\beta)=K$.
In particular, any factor of $f(x)$ in $K(\beta)[x]$ is actually in $K[x]$. But $f(x)$ is irreducible over $K$ so it must also be irreducible when considered as a polynomial in $K(\beta)[x]$.

Hence $[K(\alpha,\beta):K(\beta)]=\deg f(x)=[K(\alpha):K]$ and by the Tower Law, \[\begin{align*} [K(\alpha,\beta):K]&=[K(\alpha,\beta):K(\beta)] [K(\beta):K] \\ &=[K(\alpha):K] [K(\beta):K]. \end{align*}\]

Without the extra two conditions, we can only show that the minimal polynomial of $\alpha$ over $K(\beta)$ divides the minimal polynomial of $\alpha$ over $K$ and so $[K(\alpha,\beta):K(\beta)]\leq[K(\alpha):K]$.

Exercise 3.12 Suppose that $K$ is a field of characteristic $p>0$ and $a\in K$. Given a root $\theta$ of the polynomial $f(x)=x^p-x+a\in K[x]$, show that $K(\theta)/K$ is normal and separable.

Solution

Let $\theta$ be a root of $f(x)=x^p-x+a\in K[x]$. Since $K$ has characteristic $p$, it contains the prime subfield $\mathbb{F}_p$. Then for any $b\in\mathbb{F}_p$ we have $b^p=b$ and \[f(\theta+b)=(\theta+b)^p-(\theta+b)+a=\theta^p+b^p-\theta-b+a=0.\] In other words, the $p$ roots of $f(x)$ are $\theta, \theta+1, \theta+2,...,\theta+p-1$. These are all contained in $K(\theta)$ so $K(\theta)$ is the splitting field of $f(x)$ over $K$ and $K(\theta)/K$ is normal. Furthermore, the $p$ roots of $f(x)$ are distinct. The minimal polynomial of $\theta$ divides $f(x)$ so it also has distinct roots and the extension is separable by Theorem 4.8 in the notes.

Later, we’ll use Galois Theory to see either $\theta\in K$ or the minimal polynomial of $\theta$ is actually $f(x)$, i.e. $f(x)$ is irreducible over $K$.

Exercise 3.13 Let $L=\mathbb{F}_p(s,t)$ be the field of rational expressions in two indeterminates $s, t$ with coefficients in $\mathbb{F}_p$ where $p$ is prime. Consider the subfield $K=\mathbb{F}_p(s^p,t^p)$ of $L$.

$\;(a)\;$ Show that $[L:K]=p^2$.

$\;(b)\;$ Show that if $\gamma\in L$, then $\gamma^p\in K$. Deduce that $L/K$ is not simple.

Solution

$(a)$ Consider the tower $\;\;\;K=\mathbb{F}_p(s^p,t^p)\;\;\subset\;\;M=\mathbb{F}_p(s^p,t)\;\;\subset\;\; L=\mathbb{F}_p(s,t)$.

The polynomial $f(x)=x^p-t^p\in K[x]$ vanishes at $t$ so the minimal polynomial of $t$ over $K$ must divide $f(x)$. Now $f(x)=(x-t)^p$ so this minimal polynomial must be $(x-t)^i$ for some $1\leq i\leq p$.

If $i<p$ then $(x-t)^i=x^i+...+(-1)^it^i$ is not in $K[x]$ as $t^i\not\in K=\mathbb{F}_p(s^p,t^p)$.
Thus $i=p$, the minimal polynomial of $t$ over $K$ is $f(x)$ and $[M:K]=\deg(f(x))=p$.

Similarly, one shows that $[L:M]=p$ and hence $[L:K]=[L:M] [M:K]=p^2$.

$(b)$ If $\gamma\in L$, then $\gamma^p\in L^p\subset K$. In particular, $[K(\gamma):K]\leq p$ and so $K(\gamma)\neq L$.

3 Problem Sheet 3: Properties of field extensions

3 Problem Sheet 3:
Properties of field extensions