Topic 6 - Differential equations

Week 18 Material

Question 6.1 $\;$ Find the general solution of each of the following separable equations:

$\;(a)\;\;\dfrac{dy}{dx}=\dfrac{y}{x},\hspace{2.9cm}$ $\;(b)\;\;\dfrac{dy}{dx}=x^3y^3,\hspace{2.5cm}$ $\;(c)\;\;\dfrac{dy}{dx}=1+y^2$,

$\;(d)\;\;\dfrac{dy}{dx}=\dfrac{5x+7}{3y+2},\hspace{1.8cm}$ $\;(e)\;\;\dfrac{dy}{dx}=\dfrac{3y+2}{5x+7},\hspace{1.85cm}$ $\;(f)\;\;\dfrac{dy}{dx}=\dfrac{1+y^2}{1+x^2},$

$\;(g)\;\;x\dfrac{dy}{dx}=y-xy,\hspace{1.8cm}$ $\;(h)\;\;\dfrac{dy}{dx}=1+x+y+xy.$

Question 6.2 $\;$ Solve the following separable equations with given initial conditions:

$\;(a)\;\;(x^2+1)y\dfrac{dy}{dx}=1\;\;$ where $y(0)=-3,\hspace{0.75cm}$ $\;(b)\;\;\dfrac{dy}{dx}=3x^2e^{-y}\;\;$ where $y(-1)=0$,

$\;(c)\;\;\dfrac{dy}{dx}=\sec y\;\;$ where $y(0)=0,\hspace{2.35cm}$ $\;(d)^*\;\;\dfrac{dy}{dx}=y^2\sin x\;\;$ where $y(\pi)=-1/5$.

Question 6.3 $\;$ A wet porous substance in the open air loses its moisture at a rate proportional to the moisture content. If a sheet hung in the wind loses half its moisture during the first hour, when will it have lost 99%, assuming weather conditions remaining the same?

Question 6.4 $\;$ A hemispherical water tank of radius $R$ metres is filled with water which leaks through a circular hole of radius $r$ metres at the bottom. Torricelli’s law shows that if $h(t)$ is the depth of water in metres left in the tank after $t$ seconds, then $h(t)$ satisfies the differential equation \[\pi(2hR-h^2)\frac{dh}{dt}=-\pi r^2\sqrt{2gh}\] where $g$ is the acceleration due to gravity. Calculate the time the bowl takes to empty.

Question 6.5 $\;$ A common model for population growth is the logistic equation: \[\frac{dy}{dt}=ry(1-y/K)\] where $r$ and $K$ are positive constants. By separating variables, show that \[y(t)=\frac{Ky_0e^{rt}}{K+y_0(e^{rt}-1)}\] where $y_0=y(0)$ is the initial population. (You may assume that $y(t)$ always satisfies $0\leq y(t)<K$.)

Question 6.6 $\;$ Find the general solution of the following homogeneous equations:

$\;(a)\;\;\dfrac{dy}{dx}=\dfrac{y}{x}+\left(\dfrac{y}{x}\right)^2,\hspace{2cm}$ $\;(b)\;\;2\dfrac{dy}{dx}=\left(\dfrac{x+y}{x}\right)^2,$

$\;(c)^*\;\;\dfrac{dy}{dx}=\dfrac{y^2-x^2}{xy},\hspace{2.65cm}$ $\;(d)\;\;\dfrac{dy}{dx}=\dfrac{y^2-2xy}{x^2-2xy}.$

Question 6.7 $\;$ Find the general solution of the following linear equations:

$\;(a)\;\;\dfrac{dy}{dx}+\dfrac{y}{x}=x^2,\hspace{2.5cm}$ $\;(b)\;\;\dfrac{dy}{dx}+y\cot x=2\cos x,$

$\;(c)\;\;\dfrac{dy}{dx}+2y=e^x,\hspace{2.55cm}$ $\;(d)\;\;x\dfrac{dy}{dx}=y+x^3.$

Question 6.8 $\;$ Solve the following linear equations with initial conditions:

$\;(a)\;\;y'-y\tan x=\sec x\;\;$ where $y(0)=1,\hspace{1cm}$ $\;(b)^*\;\;xy'+y-e^x=0\;\;$ where $y(2)=1$.

Question 6.9 $\;$ The circuit pictured is a condenser consisting of a voltage source $V$ volts, a capacitor $C$ farads and two resistors $R$ and $S$ ohms.

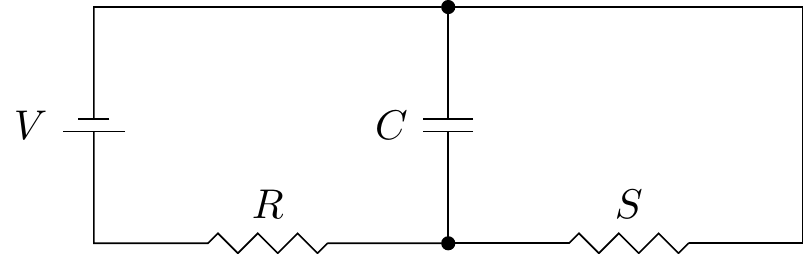
The charge $Q(t)$ at time $t$ in the circuit is known to satisfy an ODE \[RSC\frac{dQ}{dt}+(R+S)Q=SCV.\] Find a formula for $Q(t)$ given that $Q(0)=0$ coulombs, $R=5$ ohms, $S=10$ ohms, $C=10^{-3}$ farads and $V=30$ volts.

Question 6.10 $\;$ Find the general solution of the following Bernoulli equations:

$\;(a)\;\;\dfrac{dy}{dx}+\dfrac{y}{x}=xy^2\sin x,\hspace{1cm}$ $\;(b)\;\;2x\dfrac{dy}{dx}-y=10x^3y^5,\hspace{1cm}$ $\;(c)\;\;\dfrac{dy}{dx}-xy=-e^{-x^2}y^3.$

Question 6.11 $\;$ Check that the following ODEs are exact and solve them.

$\;(a)\;\;\left( x^3+2y\right) \dfrac{dy}{dx}+3x^2y+1=0,\hspace{1cm}$ $\;(b)\;\;2y\left( x^4+1\right) \dfrac{dy}{dx}+4x^3y^2-2x-1=0,$

$\;(c)^*\;\;\left(x^3\cos y\right)\dfrac{dy}{dx}+3x^2\sin y+1=0,\hspace{0.4cm}$ $\;(d)\;\;\left( x^2\sec^2 y+1\right) \dfrac{dy}{dx}+2x\tan y-\sin x=0.$

Question 6.12 $\;$ Determine if the following differential equations are exact and solve those which are:

$\;(a)\;\;(1+x^3)\dfrac{dy}{dx}+3x^2y+1=0,\hspace{1cm}$ $\;(b)\;\;y+(1+y)\dfrac{dy}{dx}=0,\hspace{1cm}$ $\;(c)\;e^{2x}\dfrac{dy}{dx}+2e^{2x}y=0,$

$\;(d)\;\;(5y-2x)\dfrac{dy}{dx}=x+2y,\hspace{1cm}$ $\;(e)\;\;e^{2x}\dfrac{dy}{dx}+2e^{2x}y+1=0.$

Question 6.13 $\;$ Solve the following mixed bag of equations.

$\;(a)\;\;\dfrac{dy}{dx}=(e^xy)^2-y,\hspace{1cm}$ $\;(b)\;\;\dfrac{dy}{dx}=y^2-5y+6,\hspace{1cm}$ $\;(c)\;\;2\dfrac{dy}{dx}=\dfrac{y}{x}+\dfrac{y^2}{x^2},\hspace{1.1cm}$

$\;(d)\;\;\dfrac{dy}{dx}=\dfrac{1+\sin y}{\cos y},\hspace{1cm}$ $\;(e)\;\;x^2\dfrac{dy}{dx}=y(x+y)\;\;$ given that $y(1)=-1,$

$\;(f)\;\;e^{-x}\cos x\dfrac{dy}{dx}-ye^{-x}\sin x=x\;\;$ given that $y(0)=0,\hspace{1cm}$

$\;(g)\;\;x(x-1)\dfrac{dy}{dx}+y=x^2e^{-x}.$

Week 19 Material

Question 6.14 $\;$ Find the general solution of each of the following:

$\;(a)\;\;y''+2y'-15y=0,\hspace{2.9cm}$ $\;(b)\;\;2y''+3y'-2y=0,$

$\;(c)\;\;y''-6y'+25y=0,\hspace{2.9cm}$ $\;(d)\;\;y''+6y'+9y=0,$

$\;(e)\;\;3y''+5y'-2y=0,\hspace{2.9cm}$ $\;(f)\;\;4y''+y=0.$

Question 6.15 $\;$ Solve the following homogeneous second order linear differential equations:

$\;(a)\;\;y''-5y'-6y=0\;\;$ with initial conditions $\;\;y(0)=5$, $y'(0)=12$.

$\;(b)\;\;3y''-8y'-3y=0\;\;$ with initial conditions $\;\;y(0)=2$, $y'(0)=-4$.

$\;(c)\;\;y''+2y'+5y=0\;\;$ with initial conditions $\;\;y(0)=1$, $y'(0)=-3$.

$\;(d)\;\;y''-4y'+29y=0\;\;$ with initial conditions $\;\;y(0)=2$, $y'(0)=-1$.

$\;(e)\;\;y''+2y'+y=0\;\;$ with initial conditions $\;\;y(0)=1$, $y'(0)=2$.

$\;(f)\;\;y''-6y'+9y=0\;\;$ with initial conditions $\;\;y(0)=2$, $y'(0)=7$.

$\;(g)\;\;y''-2y'+2y=0\;\;$ with conditions $\;\;y(0)=3$, $y(\pi/2)=0$.

(In $(g)$, instead of giving initial values for $y$ and $y'$, we have given two values for $y$ at different points - these are sometimes called boundary values.)

Question 6.16 $\;$ Find the general solution of each of the following:

$\;(a)\;\;y''+y'-2y=2e^{-x},\hspace{2.6cm}$ $\;(b)^*\;\;y''+y'-2y=e^x,$

$\;(c)\;\;y''+y'-6y=52\cos 2x,\hspace{1.75cm}$ $\;(d)\;\;2y''+3y'-2y=\sin x,$

$\;(e)\;\;y''+y=2\sin x,\hspace{3.5cm}$ $\;(f)\;\;y''-2y'+2y=e^x\cos x.$

Question 6.17 $\;$ Find complementary functions and particular integrals for the following:

$\;(a)\;\;y''+2y'-3y=4e^{-x}+26e^{2x}\cos{x},\hspace{1cm}$ $\;(b)\;\;y''+4y'+4y=32e^{2x}-2e^{-2x}.$

Question 6.18 $\;$ Solve the following inhomogeneous second order linear differential equations:

$\;(a)\;\;y''-4y'+3y=3x^2-5x+1\;\;$ with initial conditions $y(0)=4$, $y'(0)=8$.

$\;(b)\;\;y''-y'-2y=3e^{2x}\;\;$ with initial conditions $y(0)=0$, $y'(0)=-2$.

$\;(c)\;\;y''-4y'+5y=9\cos(2x)+7\sin(2x)\;\;$ with initial conditions $y(0)=0$, $y'(0)=0$.

$\;(d)\;\;y''+4y=-8\sin(2x)\;\;$ with initial conditions $y(0)=2$, $y'(0)=2$.

$\;(e)\;\;y''+4y'+4y=e^{-x}\;\;$ with initial conditions $y(0)=2$, $y'(0)=0$.

$\;(f)\;\;y''-2y'+y=xe^x \;\;$ with initial conditions $y(0)=-2$, $y'(0)=-1$.

Week 20 Material

Question 6.19 $\;\;$ Let $y(t)$ be the displacement at time $t$ of the mass in a critically damped oscillator with damping constant $c$ and mass $m=1$. If $y(0)=0$ and $y'(0)=v_0$, show that the mass will come to rest when $y=2v_0/ce$.

Question 6.20 $\;$ The differential equation for the current $I(t)$ in a series LCR circuit is \[L\dfrac{d^2I}{dt^2}+R\dfrac{dI}{dt}+\dfrac{I}{C}=\dfrac{dV}{dt}.\]

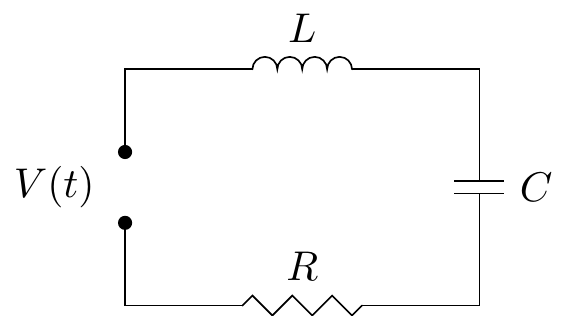
Find the current in the following cases, assuming that $I(0)=I'(0)=0$.

$\;(a)\;\;$ $R=20$, $L=10$, $C=0.05$ and $V(t)=50\sin t$.

$\;(b)\;\;$ $R=240$, $L=40$, $C=10^{-3}$ and $V(t)=369\sin(10t)$.

Question 6.21 $\;$ In an LCR circuit without a capacitor, the differential equation is first order \[L\frac{dI}{dt}+RI(t)=V(t).\] Solve this equation in the cases $\;(a)\;\;V(t)=V_0$ is constant, $\hspace{0.3cm}$ $\;(b)\;\;V(t)=V_0\sin(\omega t)$.

Comment on the long term behaviour of the current $I(t)$ in each case.

Question 6.22 $\;$ A cylindrical buoy 60 cms in diameter and weight $m$ grams floats in water with its axis vertical. When depressed slightly and released, it is found that the period of oscillation is 2 seconds. Archimedes’ principle shows that if $x(t)$ is the length of the cylinder immersed at time $t$ then $x(t)$ satisfies the equation $x''+ax=g$, where $a=900\pi g/m$ and $g=981$. Calculate the weight of the buoy and the depth of the bottom of the buoy below the waterline when the buoy is in the equilibrium position.

Question 6.23 $\;$ Solve the following systems of differential equations:

$\;(a)^*\;\;\left\{\begin{aligned} \dot{x} &= -10x+18y \\ \dot{y}&=-6x+11y \end{aligned}\right.\hspace{2.8cm}$ $\;(b)\;\;\left\{\begin{aligned} \dot{x} &= 3x+4y \\ \dot{y}&=3x+2y \\ &\text{where $x(0)=6$, $y(0)=1$} \end{aligned}\right.$

$\;(c)\;\;\left\{\begin{aligned} \dot{x} &= -x+2y \\ \dot{y}&=2x-y \\ &\text{where $x(0)=3$, $y(0)=1$} \end{aligned}\right.\hspace{0.8cm}$ $\;(d)\;\;\left\{\begin{aligned} \dot{x} &= 2x-2y-z \\ \dot{y}&=5x-3y+z \\ \dot{z}&=-4x+2y-z \end{aligned}\right.$

$\;(e)\;\;\left\{\begin{aligned} \dot{x} &= 5x+3z \\ \dot{y}&=9x+2y+9z \\ \dot{z}&=-6x-4z \end{aligned}\right.\hspace{2.6cm}$ $\;(f)\;\;\left\{\begin{aligned} \dot{x} &= x+2z \\ \dot{y}&=y-z \\ \dot{z}&=x+y+z \\ &\text{where $x(0)=y(0)=1$, $z(0)=4$} \end{aligned}\right.$