4 Galois extensions

4.1 Splitting Fields

Galois constructed his theory by considering certain “nice” symmetries of the roots of a given polynomial. He showed these formed a group (inventing the concept of a group in the process!) and properties of this group determine whether or not the polynomial can be solved in radicals. In the modern formulation of Galois Theory, these symmetries take the form of $K$-automorphisms of field extensions $L/K$. The “nice” extensions are called Galois Extensions and the corresponding $K$-automorphisms form the Galois group of the extension. We just need to decide what “nice” means…

In the last chapter, we saw how to construct field extensions containing (at least) one root of a given polynomial $f(x)\in K[x]$. The next step requires consider extensions containing all of the roots of $f(x)$.

Definition 4.1 Given a field $K$ and non-zero polynomial $f(x)\in K[x]$, a field extension $L/K$ is called a splitting field of $f(x)$ over $K$ if there are $c\in K^\times$ and $\theta_1,...,\theta_n\in L$ such that

$\;\;(i)$ $f(x)=c(x-\theta_1)\cdots(x-\theta_n)$ (we say $f(x)$ splits over $L$) and

$\;(ii)$ $L=K(\theta_1,,...\theta_n)$.

In other words, a splitting field of $f(x)$ over $K$ contains all the roots of $f(x)$ and is no bigger than it needs to be for this to happen.

Example 4.1 $(a)\;$ $\mathbb{C}$ is a splitting field for $f(x)=x^2+1$ over $\mathbb{R}$. Indeed, $f(x)=(x+i)(x-i)$ and $\mathbb{C}=\mathbb{R}(i)$. On the other hand, $\mathbb{C}$ is a not a splitting field for $x^2+1$ over $\mathbb{Q}$. It does contain the roots, but the are many other elements and $\mathbb{C}\neq\mathbb{Q}(i)$. The extension $\mathbb{C}/\mathbb{Q}$ is too big. We do however see that $\mathbb{Q}(i)$ is a splitting field for $x^2+1$ over $\mathbb{Q}$.

$(b)\;$ $\mathbb{C}$ is a splitting field for $x^4+1$ over $\mathbb{R}$. It contains all the roots, since $\mathbb{C}$ does for any polynomial. The polynomial also has non-real roots so we can’t take anything smaller that $\mathbb{C}$.

$(c)\;$ $\mathbb{Q}$ is a splitting field for $x^2-4$ over $\mathbb{Q}$. The roots are rational!

$(d)\;$ $\mathbb{Q}(i,\sqrt{2})$ is a splitting field for $f(x)=x^4-x^2-2$ over $\mathbb{Q}$. Indeed, we have \[f(x)=(x^2+1)(x^2-2)=(x+i)(x-i)(x+\sqrt{2})(x-\sqrt{2}).\]

$(e)\;$ Consider the extension $\mathbb{F}_2(\theta)/\mathbb{F}_2$ where $\theta$ is a root of $f(x)=x^3+x^2+1\in\mathbb{F}_2[x]$. In Exercise 2.7, you are asked to write $f(x)$ is a product of $3$ linear factors and $\mathbb{F}_2(\theta)$ is a splitting field for $f(x)$ over $\mathbb{F}_2$.

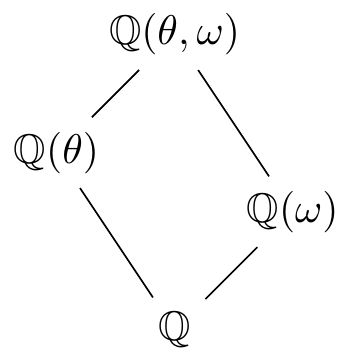
$(f)\;$ Consider a splitting field of $f(x)=x^3-2$ over $\mathbb{Q}$. It contains the three roots $\theta$, $\omega\theta$, $\omega^2\theta$ where $\theta=2^{1/3}$ and $\omega=e^{2\pi i/3}=(-1+\sqrt{-3})/2$. Notice it also contains $\omega=(\omega\theta)/\theta$ so must be $\mathbb{Q}(\theta,\omega)$. Now $\omega$ has minimal polynomial $x^2+x+1$ over $\mathbb{Q}$ so $[\mathbb{Q}(\omega):\mathbb{Q}]=2$. Combining with $[\mathbb{Q}(\theta):\mathbb{Q}]=3$, we find $[\mathbb{Q}(\theta,\omega):\mathbb{Q}]=6$. In other words, adjoining all of the roots of $x^3-2$ gives a strictly bigger extension than just adjoining one of them.

Our goal in this section is to show that every non-zero polynomial $f(x)\in K[x]$ has exactly one splitting field over a given $K$. We take the common approach to this type of problem - show there is at least one and show there is at most one. Now, showing splitting fields exist is easy for $f(x)\in\mathbb{Q}[x]$. We have a ready-made set of roots $\theta_1,...,\theta_n\in\mathbb{C}$ and we can just take $L=\mathbb{Q}(\theta_1,...,\theta_n)$. For general fields $K$, we have to do a little more work, but not much. In fact we’ll prove a slightly more precise statement, which also bounds the degree of the splitting field.

Theorem 4.1 Let $K$ be any field and $f(x)$ be a non-zero polynomial in $K[x]$ of degree $n$. Then there is a splitting field $L$ for $f(x)$ over $K$ with $[L:K]\leq n!$.

Proof. We prove this by induction on $n=\deg f(x)$. If $n=0$, then $f(x)$ is a non-zero constant, it has no roots and $K$ is a splitting field of $f(x)$ over $K$.

Now suppose $n=\deg f(x)\geq 1$. Then we can pick an irreducible factor $m(x)$ of $f(x)$ and construct an extension $K_1=K(\theta_1)$ of $K$ where $\theta_1$ is a root of $m(x)$. Notice that $[K_1:K]=\deg m(x)$ and $f(x)=(x-\theta_1)f_1(x)$ for some $f_1(x)\in K_1[x]$. Now $\deg f_1(x)=n-1$ so by the induction hypothesis, there is a splitting field $L$ for $f_1(x)$ over $K_1$ with $[L:K_1]\leq (n-1)!$. That means there are $\theta_2,...,\theta_n$ such that $L=K_1(\theta_2,...,\theta_n)$ and \[f_1(x)=c(x-\theta_2)\cdots(x-\theta_n)\in K_1[x].\] But then $K_1=K(\theta_1)$ implies $L=K(\theta_1,\theta_2,...,\theta_n)$ and \[f(x)=c(x-\theta_1)(x-\theta_2)\cdots(x-\theta_n)\in K[x].\] Finally, using the Tower Law, \[\begin{align*} [L:K] = [L:K_1] [K_1:K] \leq (n-1)!\cdot\deg m(x) \leq (n-1)!\cdot\deg f(x)=n!\tag*{$\square$} \end{align*}\]

We are left with the harder task of proving splitting fields are unique, where as always, we really mean unique up to isomorphism. Again, we will prove this by induction on $\deg f(x)$. First, a bit of notation: given a field homomorphism $\sigma:K\rightarrow K'$ and a polynomial $f(x)\in K[x]$, write $\sigma_* f(x)$ for the polynomial formed by applying $\sigma$ to the coefficients of $f(x)$. Explicitly, \[f(x)=\sum_ia_ix^i\in K[x]\quad\implies\quad \sigma_* f(x)=\sum_i\sigma(a_i)x^i\in K'[x].\] The induction step in our proof will use the following Lemma concerning simple extensions.

Lemma 4.1 Suppose $\sigma:K\to K'$ is a field isomorphism. Let $K(\theta)/K$ be a simple extension where $\theta$ has minimal polynomial $m(x)\in K[x]$ and let $\theta'$ be a root of $\sigma_*m(x)$. Then there is a (unique) field isomorphism $\tau:K(\theta)\to K'(\theta')$ such that $\tau(\theta)=\theta'$ and $\tau(a)=\sigma(a)$ for each $a\in K$.

In other words, an isomorphism $K\;\tilde{\longrightarrow}\; K'$ can be extended to an isomorphism $K(\theta)\;\tilde{\longrightarrow}\; K'(\theta')$.

Proof. Consider $K'(\theta')$ as an extension of $K$ via the composition of $\sigma:K\to K'$ with the inclusion map $K'\to K'(\theta')$. Then the minimal polynomial of $\theta'$ over $K$ is $m(x)$. Using the universal property of simple extensions (Proposition 3.1) then gives a (unique) field isomorphism with the required properties.

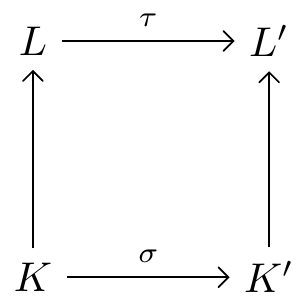
Theorem 4.2 Given an isomorphism of fields $\sigma:K\to K'$ and non-zero polynomial $f(x)\in K[x]$, let $L$ be a splitting field for $f(x)$ over $K$ and $L'$ be a splitting field for $\sigma_*f(x)$ over $K'$. Then there is a field isomorphism $\tau:L\to L'$ such that $\tau(a)=\sigma(a)$ for all $a\in K$.

In other words, an isomorphism $K\;\tilde{\longrightarrow}\; K'$ can be extended to an isomorphism $L\;\tilde{\longrightarrow}\; L'$. We can show this in the following diagram where the vertical arrows are the natural inclusion maps

Proof. We proceed by induction on $n=\deg f(x)=\deg \sigma_*f(x)$. If $n=0$, then these polynomials have no roots so $L=K$, $L'=K'$ and we can take $\tau=\sigma$.

Now suppose $n=\deg f(x)\geq 1$. Choose an irreducible factor $m(x)$ of $f(x)$. This implies $\sigma_*m(x)$ is an irreducible factor of $\sigma_*f(x)$. Choose a root $\theta$ of $m(x)$ in $L$ and a root $\theta'$ of $\sigma_*m(x)$ in $L'$. The previous Lemma then provides a field isomorphism \[\tau_1:K(\theta)\to K'(\theta')\qquad\text{where $\;\tau_1(\theta)=\theta'$, $\;\tau_1(a)=\sigma(a)$ for each $a\in K$.}\] We will use this to construct the required isomorphism $\tau:L\to L'$ as in the following diagram:

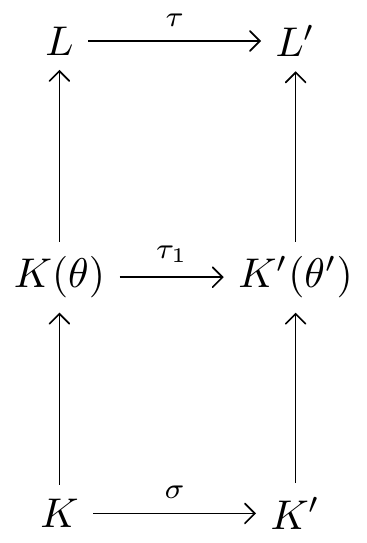
Now $\theta$ is a root of $f(x)$ so write $f(x)=(x-\theta)f_1(x)$ for some $f_1(x)\in K(\theta)[x]$. Then \[\sigma_*f(x)=\tau_{1*}f(x)=(x-\theta')\tau_{1*}f_1(x)\] where $\tau_{1*}f_1(x)\in K'(\theta')[x]$. We now notice that $L$ is the splitting field of $f_1(x)$ over $K(\theta)$ and $L'$ is the splitting field of $\tau_{1*}f_1(x)$ over $K'(\theta')$. Since $\deg f_1(x)=n-1$, the induction hypothesis gives an isomorphism $\tau:L\to L'$ with $\tau(\alpha)=\tau_1(\alpha)$ for $\alpha\in K(\theta)$. This is the isomorphism we require, since $\tau(a)=\sigma(a)$ for all $a\in K$.

In the particular case where $K=K'$ and $\sigma$ is the identity map, we obtain the uniqueness of the splitting field of $f(x)$ over $K$.

Remark. By being more careful, one can show that there are at most $[L:K]$ isomorphisms $\tau:L\to L'$ extending $\sigma:K\to K'$ as in the Theorem.

4.2 Normal extensions

The first (and most important) “nice” property we want our field extensions to have is normality:

Definition 4.2 A field extension $L/K$ is called normal if the following condition holds:

whenever $f(x)\in K[x]$ is irreducible and has a root in $L$, then all of its roots are in $L$. In particular, $f(x)$ splits completely as a product of linear factors in $L[x]$.

In other words, the minimal polynomial over $K$ of any $\theta\in L$ has all of its roots in $L$, and can be written as a product of linear factors in $L[x]$.

Example 4.2 $(a)$ If $[L:K]=1$, then $L/K$ is normal. This should be clear since $L=K$.

$(b)$ If $[L:K]=2$, then $L/K$ is normal. This only requires a short argument: suppose $\theta\in L$ has minimal polynomial $m(x)\in K[x]$. Then $K\subset K(\theta)\subset L$ and so $\deg m(x)=[K(\theta):K]=1$ or $2$.

If $\deg m(x)=1$, then there is nothing to prove, as $m(x)$ is already linear.
If $\deg m(x)=2$, then $m(x)=(x-\theta)m_1(x)$ where $m_1(x)\in L[x]$ is linear. Thus $m(x)$ splits completely in $L[x]$.

$(c)$ If $[L:K]=3$, then $L/K$ might not be normal. Indeed, we’ve already seen the example $\mathbb{Q}(\theta)/\mathbb{Q}$ where $\theta$ is a root of $m(x)=x^3-2$.

The other two roots are $\omega\theta$, $\omega^2\theta$ where $\omega=e^{2\pi i/3}$ and if $\omega\theta\in\mathbb{Q}(\theta)$, then $\omega=(\omega\theta)/\theta\in\mathbb{Q}(\theta)$ as well. This implies $\mathbb{Q}\subset\mathbb{Q}(\omega)\subset\mathbb{Q}(\theta)$ which is impossible as $[\mathbb{Q}(\omega):\mathbb{Q}]=2$ doesn’t divide $[\mathbb{Q}(\theta):\mathbb{Q}]=3$.

$(d)$ Suppose $\theta\in\mathbb{C}$ is any root of the irreducible cubic $f(x)=x^3-3x-1\in\mathbb{Q}[x]$. Let’s show directly that $L=\mathbb{Q}(\theta)$ contains all of the roots of $f(x)$, using Cardano’s formulas (the method for solving cubic equations in the Introduction section 1.2).

Recall we set $\theta=u+v$ and use the identity $(u+v)^3-3uv(u+v)-(u^3+v^3)=0$. In this case, we require $uv=1$ and $u^3+v^3=1$ and find $u^3,v^3$ by solving the quadratic equation \[(y-u^3)(y-v^3)=y^2-y+1=0\quad\implies u^3, v^3=\frac{1}{2}(1\pm i\sqrt{3})=e^{\pm\pi i/3}.\] The three roots of our cubic polynomial are then $u+v$, $\omega u+\omega^2 v$, $\omega^2u+\omega v$ where $\omega=e^{2\pi i/3}$. Explicitly, these are \[e^{\pi i/9}+e^{-\pi i/9},\quad e^{7\pi i/9}+e^{-7\pi i/9},\quad\text{and}\quad e^{13\pi i/9}+e^{-13\pi i/9}.\] We can write these in trigonometric form as $\theta_1=2\cos(\pi/9)$, $\theta_2=2\cos(7\pi/9)$ and $\theta_3=2\cos(13\pi/9)$, and, using the double angle formula, \[\theta_2=2\cos(\pi-2\pi/9)=-2\cos(2\pi/9)=-2[2\cos^2(\pi/9)-1]=-\theta_1^2+2.\] Also, $\theta_1+\theta_2+\theta_3=0$ so $\theta_3=\theta_1^2-\theta_1-2$ and we’ve found that $\theta_2,\theta_3\in\mathbb{Q}(\theta_1)$. We could similarly show $\theta_i\in\mathbb{Q}(\theta_j)$ for each $i,j$, and hence if a field extension contains one root, then it contains them all.

Unfortunately, this doesn’t tell us that $L=\mathbb{Q}(\theta)/\mathbb{Q}$ is normal. We’ve checked that all the roots of $f(x)=x^3-3x-1$ are in $L$, but for normality, we need every irreducible polynomial with a root in $L$ to have all its roots in $L$. Fortunately, the splitting fields from the last section come to our rescue.

Theorem 4.3 (Normality Criterion) A field extension $L/K$ is finite and normal if and only if $L$ is the splitting field for some non-zero polynomial $f(x)\in K[x]$ over $K$.

Proof. Suppose that $L/K$ is finite and normal. By finiteness, there is a basis of $L/K$ consisting of elements $\theta_1,...,\theta_n\in L$ which are algebraic over $K$. Let $m_i(x)\in K[x]$ be the minimal polynomial of $\theta_i$ and consider the product \[f(x)=m_1(x)\cdots m_n(x)\in K[x].\] Since $L/K$ is normal, each $m_i(x)$ splits completely as a product of linear factors in $L[x]$, so $f(x)$ does as well. The set of roots of $f(x)$ in $L$ contains $\theta_1,...,\theta_n$ and $L=K(\theta_1,...,\theta_n)$, so $L$ is generated by the set of roots of $f(x)$ in $L$. Hence, $L$ is a splitting field for $f(x)$ over $K$.

In the other direction, suppose $L$ is a splitting field for some $f(x)\in K[x]$ over $K$. Then $f(x)=c(x-\theta_1)\cdots(x-\theta_n)$ for some $\theta_1,...,\theta_n\in L$ and $L=K(\theta_1,...,\theta_n)$. Each $\theta_i$ is algebraic (since it is the root of a polynomial) and so $L/K$ is finite.

Now to prove normality: given $\delta\in L$ with minimal polynomial $m(x)\in K[x]$, we need to show that $m(x)$ splits into linear factors in $L[x]$. In other words, for any other root $\varepsilon$ of $m(x)$, we need to show $\varepsilon\in L$.

Step 1: As $\delta$, $\varepsilon$ are roots of $m(x)$, the universal property of simple extensions gives an isomorphism \[\sigma: K(\delta)\to K(\varepsilon) \quad\text{with $\sigma(\delta)=\varepsilon$ and $\sigma(a)=a$ for $a\in K$.}\] Notice $[K(\delta):K]=[K(\varepsilon):K]=\deg m(x)$.

Step 2: We have $\begin{cases} L(\delta)=K(\delta,\theta_1,...,\theta_n)=K(\delta)(\theta_1,...,\theta_n) \\ L(\varepsilon)=K(\varepsilon,\theta_1,...,\theta_n)=K(\varepsilon)(\theta_1,...,\theta_n) \end{cases}$

so we see $L(\delta)$ is a splitting field for $f(x)$ over $K(\delta)$ and $L(\varepsilon)$ is a splitting field for $f(x)$ over $K(\varepsilon)$.

Step 3: By the uniqueness of splitting fields theorem, the isomorphism $\sigma:K(\delta)\to K(\varepsilon)$ extends to an isomorphism $\tau:L(\delta)\to L(\varepsilon)$. In particular, $[L(\delta):K(\delta)]=[L(\varepsilon):K(\varepsilon)]$. Using $\delta\in L$ and the Tower Law, we have \[\begin{align*} [L:K]=[L(\delta):K] &= [L(\delta):K(\delta)] [K(\delta):K] \\ &=[L(\varepsilon):K(\varepsilon)] [K(\varepsilon):K] \\ &=[L(\varepsilon):K] \\ &=[L(\varepsilon):L] [L:K]. \end{align*}\] We’ve found that $[L(\varepsilon):L]=1$, i.e. $L(\varepsilon)=L$ and so $\varepsilon\in L$ as required.

Example 4.3 $(a)$ The extension $\mathbb{Q}(\sqrt{2},\sqrt{3},\sqrt{5},\sqrt{7})/\mathbb{Q}$ is normal. Indeed it is the splitting field of \[f(x)=(x^2-2)(x^2-3)(x^2-5)(x^2-7)\in\mathbb{Q}[x].\]

$(b)$ The extension $\mathbb{Q}(\sqrt[3]{2})/\mathbb{Q}$ is not normal. The irreducible polynomial $x^3-2\in\mathbb{Q}[x]$ has only one root in $\mathbb{Q}(\sqrt[3]{2})$. However, the extension $\mathbb{Q}(\sqrt[3]{2},\omega)/\mathbb{Q}$ is normal (where as usual, $\omega=e^{2\pi i/3}$) since it is the splitting field of $x^3-2\in\mathbb{Q}$.

$(c)$ Similarly, the extension $\mathbb{Q}(\sqrt[4]{2})/\mathbb{Q}$ is not normal whereas $\mathbb{Q}(\sqrt[4]{2},i)/\mathbb{Q}$ is normal.

$(d)$ Let $\theta$ be any root of $f(x)=x^3-3x-1\in\mathbb{Q}[x]$. We showed earlier that $\mathbb{Q}(\theta)$ contains all the roots of $f(x)$, so is the splitting field of $f(x)$ and hence $\mathbb{Q}(\theta)/\mathbb{Q}$ is normal.

$(e)$ Similarly, let $\theta$ be any root of $f(x)=x^3+x^2+1\in\mathbb{F}_2[x]$. In Exercise 2.7, you show that $\mathbb{F}_2(\theta)$ contains all the roots of $f(x)$, so is the splitting field of $f(x)$ and the extension $\mathbb{F}_2(\theta)/\mathbb{F}_2$ is normal. (Next term, we will see that all finite extensions of $\mathbb{F}_p$ are normal.)

$(f)$ Let $K=\mathbb{F}_p(t)$ be the field of rational expressions over $\mathbb{F}_p$ with indeterminate $t$. Then the polynomial $f(x)=x^p-t\in K[x]$ is irreducible and, for a root $\theta$ of $f(x)$, the extension $L=K(\theta)$ is normal over $K$. Indeed, since we are in characteristic $p$, \[f(x)=x^p-t=x^p-\theta^p=(x-\theta)^p\] and so $f(x)$ splits into linear factors in $L[x]$. That means $L$ is the splitting field for $f(x)$ over $K$ and so $L/K$ is normal.

In examples $(b)$ and $(c)$, there was a non-normal extension embedded in a larger, normal extension. We call a field $N$ a normal closure of $L/K$ if $K\subset L\subset N$ with $N/K$ normal and furthermore, $N$ is minimal in the sense that $K\subset L\subset N'\subset N$ with $N'/K$ normal implies $N'=N$. Just as with splitting fields, these are unique.

Theorem 4.4 Let $L/K$ be a finite extension. Then there is a normal closure of $L/K$ and it is unique up to a $K$-isomorphism.

Proof. We have $L=K(\alpha_1,...,\alpha_n)$ where $\alpha_1,...,\alpha_n$ are algebraic over $K$. Let $m_i(x)\in K[x]$ be the minimal polynomial of $\alpha_i$ and set $f(x)=m_1(x)\cdots m_n(x)$. It’s not hard to see that the splitting field $N$ of $f(x)$ over $K$ is a normal closure. Each $m_i(x)$ splits in $N$ so it contains their splitting fields and furthermore, we couldn’t take any smaller field $N$. The uniqueness up to $K$-isomorphism follows from the uniqueness of splitting fields discussed earlier.

We’ve mentioned before that the symmetries in Galois theory are given by certain automorphisms. Recall that a $K$-automorphism of a field extension $L/K$ is a field isomorphism $\sigma:L\to L$ where $\sigma|_K=\id$, i.e. the restriction of $\sigma$ to $K$ is the identity: $\sigma(a)=a$ for all $a\in K$. It’s straight-forward to check that the set of $K$-automorphisms of $L/K$ forms a group under composition (check that it includes the identity map and is closed under composition and taking inverses).

Definition 4.3 We write $\Aut(L/K)$ for the group of $K$-automorphisms of $L/K$ with composition as the group operation.

Example 4.4 $(a)$ The group $\Aut(\mathbb{C}/\mathbb{R})$ contains at least two elements: as always, there is the identity map $\id(a+bi)=a+bi$ and we also have complex conjugation $\sigma(a+bi)=a-bi$ for $a,b\in\mathbb{R}$. In fact, there are no others. Indeed, suppose we have any $\mathbb{R}$-automorphism $\tau:\mathbb{C}\to\mathbb{C}$. Then \[\tau(i)^2=\tau(i^2)=\tau(-1)=-1 \quad\implies\quad \tau(i)=\pm i.\] Then for $a,b\in\mathbb{R}$, we have $\tau(a+bi)=\tau(a)+\tau(b)\tau(i)=a\pm bi$ leading to either the identity or complex conjugation. In particular, $\Aut(\mathbb{C}/\mathbb{R})=\{\id, \sigma\}\cong\mathbb{Z}/2$.

$(b)$ Similarly, we find $\Aut(\mathbb{Q}(\sqrt{2})/\mathbb{Q})=\{\id, \sigma\}\cong\mathbb{Z}/2$ where $\id(a+b\sqrt{2})=a+b\sqrt{2}$ and $\sigma(a+b\sqrt{2})=a-b\sqrt{2}$ for $a,b\in\mathbb{Q}$. More generally, look back at Section 1.4. There we had an irreducible $f(x)=x^2+px+q\in\mathbb{Q}[x]$ with distinct roots $\theta,\theta'\in\mathbb{C}$ and considered the quadratic extension $\mathbb{Q}(\theta)/\mathbb{Q}$. We then constructed a $\mathbb{Q}$-automorphism $\sigma(a+b\theta)=a+b\theta'$ for $a,b\in\mathbb{Q}$. As above, we can show any $\mathbb{Q}$-automorphism $\tau:\mathbb{Q}(\theta)\to\mathbb{Q}(\theta)$ must have $\tau(\theta)=\theta$ or $\theta'$ so $\tau$ must be either the identity or $\sigma$. Again we have $\Aut(\mathbb{Q}(\theta)/\mathbb{Q})=\{\id, \sigma\}\cong\mathbb{Z}/2$.

$(c)$ Let $\theta=\sqrt[3]{2}$ and consider $\sigma\in\Aut(\mathbb{Q}(\theta)/\mathbb{Q})$. Then \[\sigma(\theta)^3=\sigma(\theta^3)=\sigma(2)=2\] and $\sigma(\theta)\in\mathbb{Q}(\theta)\subset\mathbb{R}$. Hence we have $\sigma(\theta)=\theta$ and so $\sigma$ is the identity! $\Aut(\mathbb{Q}(\theta)/\mathbb{Q})$ is the trivial group with one element. This isn’t a very useful situation, given that we hope to use automorphisms to study field extensions. The issue is that $\mathbb{Q}(\theta)/\mathbb{Q}$ is not normal and so not nice enough. Later, we will rectify this by considering the normal closure $\mathbb{Q}(\sqrt[3]{2},\omega)/\mathbb{Q}$ where $\omega=e^{2\pi i/3}$.

$(d)$ Let $\theta^p=t$ and consider $\sigma\in\Aut(\mathbb{F}_p(\theta)/\mathbb{F}_p(t))$. Then \[\sigma(\theta)^p=\sigma(\theta^p)=\sigma(t)=t=\theta^p\] and so $(\sigma(\theta)-\theta))^p=\sigma(\theta)^p-\theta^p=0$ so $\sigma(\theta)=\theta$. Arbitrary elements of $\mathbb{F}_p(\theta)$ are of the form $c_0+c_1\theta+\cdots+c_{p-1}\theta^{p-1}$ and we find that $\sigma$ doesn’t change them! In other words, $\Aut(\mathbb{F}_p(\theta)/\mathbb{F}_p(t))$ is the trivial group. We won’t be able to fix this by taking a normal closure, since $\mathbb{F}_p(\theta)/\mathbb{F}_p(t)$ is already normal.

$(e)$ Consider the infinite extension $\mathbb{R}/\mathbb{Q}$ and a $\mathbb{Q}$-automorphism $\sigma:\mathbb{R}\to\mathbb{R}$. What can we say about this? The answer is quite surprising, once we remember the special properties of $\mathbb{R}$ - it is a complete ordered field. Given $\alpha, \beta\in\mathbb{R}$, we have \[\begin{align*} \alpha\leq\beta &\quad\implies\quad \beta-\alpha=\gamma^2\quad\text{for some $\gamma\in\mathbb{R}$} \\ &\quad\implies\quad \sigma(\beta)-\sigma(\alpha)=\sigma(\beta-\alpha)=\sigma(\gamma^2)=\sigma(\gamma)^2\geq 0 \\ &\quad\implies\quad \sigma(\alpha)\leq\sigma(\beta). \end{align*}\] Now given $\alpha\in\mathbb{R}$, let $r_n,s_n\in\mathbb{Q}$ be sequences of rational numbers with $r_n\leq\alpha\leq s_n$ and $r_n\to\alpha$, $s_n\to\alpha$ as $n\to\infty$. Then \[r_n=\sigma(r_n)\leq\sigma(\alpha)\leq\sigma(s_n)=s_n\] and using the Squeezing Theorem, we find $\sigma(\alpha)=\alpha$. In other words, $\Aut(\mathbb{R}/\mathbb{Q})$ is the trivial group! On the other hand $\Aut(\mathbb{C}/\mathbb{Q})$ is not the trivial group since it contains complex conjugation. Actually this automorphism group is infinite, though it’s hard to explicitly find automorphisms other than the identity and complex conjugation. (It relies heavily on the Axiom of choice.)

For simple algebraic extensions as in examples $(a),(b),(c),(d)$, we have the following result bounding the number of $K$-automorphisms.

Theorem 4.5 Suppose $L=K(\theta)$ where $\theta$ is a root of an irreducible polynomial $f(x)\in K[x]$ of degree $n=\deg f(x)$. Then $|\Aut(L/K)|\leq n$ and we have equality precisely when $f(x)$ has $n$ distinct roots in $L$.

Proof. Any element $\alpha\in L$ can be written (uniquely) as \[\alpha=c_0+c_1\theta+...+c_{n-1}\theta^{n-1} \quad\text{where $c_0,...,c_{n-1}\in K$.}\] Applying $\sigma\in\Aut(L/K)$ to this gives \[\sigma(\alpha)=c_0+c_1\sigma(\theta)+...+c_{n-1}\sigma(\theta)^{n-1}.\] In other words, $\sigma(\alpha)$ is completely determined by $\sigma(\theta)$. However, $\sigma(\theta)\in L$ and $\sigma(\theta)$ is also a root of $f(x)$ since, \[\begin{align*} f(x)=a_nx^n+a_{n-1}x^{n-1}&+\cdots+a_1x+a_0\in K[x] \\ \implies f(\sigma(\theta))&=a_n\sigma(\theta)^n+a_{n-1}\sigma(\theta)^{n-1}+\cdots+a_1\sigma(\theta)+a_0 \\ &=\sigma(a_n\theta^n+a_{n-1}\theta^{n-1}+\cdots+a_1\theta+a_0)=\sigma(f(\theta))=0. \end{align*}\] Thus $\sigma$ is completely determined by choosing one of the roots of $f(x)$. There are at most $n$ of these, and there are exactly $n$ choices for $\sigma$ precisely when $f(x)$ has $n$ distinct roots in $L$.

This result can be generalised to arbitrary field extensions of finite degree.

Theorem 4.6 Suppose $L/K$ is a field extension of finite degree. Then $|\Aut(L/K)|\leq [L:K]$ and we have equality exactly when $L/K$ is normal and the minimal polynomial of any $\theta\in L$ over $K$ has no repeated roots.

We won’t prove this, but point out it is done via a more detailed version of the uniqueness of splitting fields proof in Theorem 4.2.

4.3 Separable extensions

In order to fully exploit the symmetries of a field extension $L/K$, it would be nice to have many $K$-automorphisms available. The previous Theorem 4.6 suggests we should consider when minimal polynomials have no repeated roots. This is our second “nice” property of field extensions:

Definition 4.4 Let $L/K$ be a field extension of finite degree.

$\;(i)$ An element $\theta\in L$ is separable over $K$ if its minimal polynomial over $K$ has no repeated roots (in its splitting field).

$(ii)$ The extension $L/K$ is called separable if every element of $L$ is separable over $K$.

In particular, Theorem 4.6 then says a finite extension $L/K$ has the maximal possible number $[L:K]$ of $K$-automorphisms exactly when $L/K$ is both normal and separable.

Separability might seem to be a strange condition - how can an irreducible polynomial $f(x)\in K[x]$ have a factor $(x-\theta)^2$ for some $\theta$ in the splitting field of $f(x)$ over $K$? We’ve actually already seen an example in the last section.

Example 4.5 Let $K=\mathbb{F}_p(t)$ be the field of rational expressions over $\mathbb{F}_p$ with indeterminate $t$. Then the polynomial $f(x)=x^p-t\in K[x]$ is irreducible (e.g. by Eisenstein’s Criterion) and \[f(x)=x^p-t=x^p-\theta^p=(x-\theta)^p\] so $\theta$ is a root of multiplicity $p\geq 2$. Hence the extension $\mathbb{F}_p(\theta)/\mathbb{F}_p(t)$ is normal but not separable.

We will see that this is pretty much the simplest example exhibiting this behaviour and that most of the extensions we’ve met are separable. First, recall in real analysis we can detect when a function $f(x)$ has repeated roots via differentiation - look for where $f(x)$ and $df/dx$ both vanish. Now, there is no general notion of a limit (and hence derivative) over a general field $K$. However, since we only need to consider polynomials, we can restrict to a purely algebraic version.

Definition 4.5 Given a polynomial $f(x)=\sum_{i=0}^na_ix^i\in K[x]$, the formal derivative of $f(x)$ is \[Df(x)=\sum_{i=1}^n ia_ix^{i-1}\in K[x]\]

We use this notation $Df$ rather than $f'$ to remind ourselves not to accidentally take the familiar properties of derivatives for granted. Now it’s easy to check the most useful properties do hold, for instance, try showin that \[D(f+g)=Df+Dg,\quad D(fg)=f\cdot Dg+Df\cdot g,\quad D(a)=0\;\;\text{for $a\in K$.}\] It’s also clear that $\deg Df(x)<\deg f(x)$. However, if $K$ has positive characteristic $p$, we don’t necessarily have $\deg Df(x)=(\deg f(x))-1$. For instance, $D(x^p)=px^{p-1}=0$.

We can use this formal derivative tool to show that finite extensions are separable under quite general conditions.

Theorem 4.7 (Sufficient conditions for separability) A finite extension $L/K$ is automatically separable in the following cases:

$\;\;\;(i)$ $\ch(K)=0$,

$\;\;(ii)$ $\ch(K)=p$ and $K=K^p$, i.e. every element $a\in K$ is a $p\,$th power $a=b^p$ for some $b\in K$,

$\;(iii)$ $\ch(K)=p$ and $[L:K]$ is not divisible by $p$.

Proof. Under each condition, we need to show that for any element $\theta\in L$, its minimal polynomial over $K$ \[f(x)=x^n+a_{n-1}x^{n-1}+\cdots+a_1x+a_0\in K[x]\] has no repeated roots. Suppose on the contrary that $f(x)$ has a repeated root $\alpha$ in the splitting field of $f(x)$ over $K$. Note that $\alpha$ has the same minimal polynomial $f(x)$ as $\theta$ since $f(\alpha)=0$ and $f(x)$ is irreducible.

We have $f(x)=(x-\alpha)^2g(x)$ for some $g(x)$ with coefficients in the splitting field of $f(x)$ over $K$. Then \[Df(x)=(x-\alpha)^2Dg(x)+2(x-\alpha)g(x)\quad\implies\quad Df(\alpha)=0.\] But $f(x)$ is the minimal polynomial of $\alpha$ and $\deg Df(x)<\deg f(x)$. Hence \[Df(x)=nx^{n-1}+(n-1)a_{n-1}x^{n-2}+\cdots+2a_2x+a_1\] must be the zero polynomial and its coefficients $n$ and $ia_i$ for $1\leq i\leq n-1$ must all equal zero in $K$.

$(i)$ When $\ch(K)=0$, it is impossible to have $n=0$ in $K$ and so $f(x)$ cannot have a repeated root.

$(ii)$ When $\ch(K)=p$, we see that $ia_i=0$ implies $a_i=0$ when $i$ is not a multiple of $p$ and so $f(x)$ is actually a polynomial in $x^p$. Thus $n=mp$ and \[f(x)=x^{mp}+a_{(m-1)p}x^{(m-1)p}+\cdots+a_{2p}x^{2p}+a_px^p+a_0.\] If every element of $K$ is a $p\,$th power, then $a_{jp}=b_j^p$ for some $b_j\in K$ and \[\begin{align*} f(x)&=x^{mp}+b_{m-1}^px^{(m-1)p}+\cdots+b_2^px^{2p}+b_1^px^p+b_0^p \\ &=\left(x^m+b_{m-1}x^{(m-1)}+\cdots+b_2x^{p^2}+b_1x^p+b_0\right)^p. \end{align*}\] This means $f(x)$ is not irreducible in $K[x]$ and we get a contradiction.

$(iii)$ Finally, if $\ch(K)=p$ and $[L:K]$ is not divisible by $p$, then neither is \[n=\deg f(x)=[K(\alpha):K]\] since this divides $[L:K]$. But then $n\neq 0$ in $K$ which again gives a contradiction.

Remark. Fields satisfying either condition $(i)$ or $(ii)$ are sometimes called perfect and we’ve shown finite extensions of perfect fields are always separable. As well as characteristic $0$ fields, this includes $K=\mathbb{F}_p$ for $p$ prime since Fermat’s Little Theorem says $a=a^p$ for every $a\in\mathbb{F}_p$. Next term, we’ll see that every finite field ($\mathbb{F}_q$ where $q$ is a power of a prime) is also perfect. Thus, the only chance we have to find an extension which isn’t separable is to take an infinite field of characteristic $p$, e.g. $K=\mathbb{F}_p(t)$. Furthermore, taking condition $(iii)$ into account, we should look at extensions which have degree a multiple of $p$. The first example we might try is $\mathbb{F}_p(\theta)/\mathbb{F}_p(t)$ where $\theta^p=t$ and indeed this isn’t separable.

Proving necessary and sufficient conditions for separability is somewhat harder.

Theorem 4.8 Let $L=K(\alpha)$ where $\alpha\in L$ has minimal polynomial $m(x)\in K[x]$. Then $L/K$ is separable if and only if $\alpha$ is separable over $K$, i.e. $m(x)$ has no repeated roots in the splitting field of $m(x)$ over $K$. More generally, $L=K(\alpha_1,...,\alpha_n)/K$ is separable if and only if each $\alpha_i$ is separable over $K$.

Proof. The “only if” part of the general case follows directly from the definition of separability.

The “if” part is not at all straight-forward! We will only prove it for the simple case $L=K(\alpha)$ - for the general case, see one of the texts in the reading list.

We are given $L=K(\alpha)$ where the minimal polynomial $m(x)\in K[x]$ of $\alpha$ has no repeated roots and need to show the minimal polynomials of any element of $L$ has no repeated roots.

Suppose on the contrary that some $\theta\in L$ has minimal polynomial $f(x)\in K[x]$ with a repeated root. As in the proof of the previous Theorem, this is quite exceptional - it can only happen when $\ch(K)=p>0$ and $f(x)=g(x^p)$ for some $g(x)\in K[x]$. Notice that $g(x)$ is the minimal polynomial of $\theta^p$ over $K$ since $g(\theta^p)=f(\theta)=0$ and $g(x)$ is irreducible (if it was reducible, then $f(x)$ would be as well). Hence \[ [K(\theta):K]=\deg f(x)=p\cdot\deg g(x)=p\cdot[K(\theta^p):K] \] and so $[K(\theta):K(\theta^p)]=p$. Here is how the fields fit together:

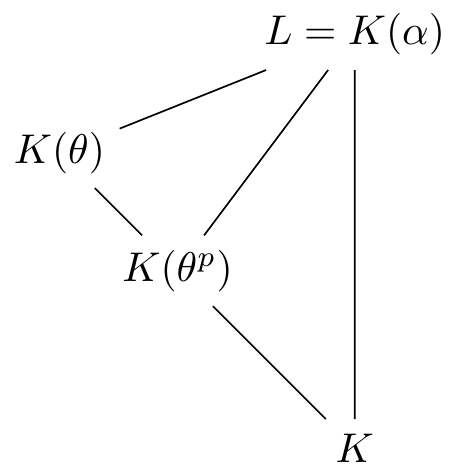
Now let $m_1(x)\in K(\theta)[x]$ be the minimal polynomial of $\alpha$ over $K(\theta)$. Consider $m_1(x)^p$ and notice

it has coefficients in $K(\theta^p)$ and has $\alpha$ as a root,
it has degree $p\cdot\deg m_1(x)=p\cdot [L:K(\theta)]=[L:K(\theta)] [ K(\theta):K(\theta^p)]=[L:K(\theta^p)]$.

This means $m_1(x)^p$ is actually the minimal polynomial of $\alpha$ over $K(\theta^p)$. Finally, we notice $m_1(x)^p$ now divides $m(x)$ in $L[x]$. But then $m(x)$ has repeated factors, contradicting the initial assumption that it has no repeated roots.

Remark. Separability works nicely in towers. Using the methods of this section, we can show that given finite extensions $K\subset M\subset L$, then $L/K$ is separable if and only if both $L/M$ and $M/K$ are separable (see Exercise 3.8 on the Problems Sheet). On the other hand, normality in towers isn’t quite so well-behaved (see Exercise $3.6$).

We end the section by stating (without proof) the following very nice fact about separable extensions.

Theorem 4.9 (Theorem of the Primitive Element) Suppose that $L/K$ is finite and separable. Then $L/K$ is simple, i.e. there exists $\alpha\in L$ such that $L=K(\alpha)$.

We’ve already seen an example of this at the end of the last chapter where we showed that $\mathbb{Q}(\sqrt{2},\sqrt{7})=\mathbb{Q}(\sqrt{2}+\sqrt{7})$. More generally, the proof of the above theorem shows that if $\alpha,\beta$ are algebraic over $\mathbb{Q}$, then $\mathbb{Q}(\alpha,\beta)=\mathbb{Q}(\alpha+c\beta)$ for some $c\in \mathbb{Q}$.

Considering the sufficient conditions for separability from earlier, we have to go out of our way to find examples of extensions $L/K$ where there is no $\alpha\in L$ such that $L=K(\alpha)$. Here’s one: let $L=\mathbb{F}_2(s,t)$ be the field of rational expressions in two indeterminates $s, t$ and $K=\mathbb{F}_2(s^2,t^2)$. Try showing that $L/K$ is not simple (see Exercise 3.13 in the Problem Sheets).

4.4 The Fundamental Theorem of Galois Theory

Definition 4.6 A finite extension $L/K$ is called a Galois extension if it is both normal and separable. In that case, we write $\Gal(L/K)$ for the automorphism group $\Aut(L/K)$ and call it the Galois group of the extension.

Equivalently, by Theorem 4.6, a finite extension is Galois if and only if $|\Aut(L/K)|=[L:K]$. Recall an intermediate field of an extension $L/K$ is a subfield of $L$ containing $K$. The Fundamental Theorem of Galois Theory relates the set of intermediate fields \[\mathcal{F}=\{\text{intermediate fields of $L/K$}\}\] with the set of subgroups of $\Gal(L/K)$ \[\mathcal{G}=\{\text{subgroups of $\Gal(L/K)$}\}.\] We’ll draw corresponding diagrams of fields and groups as follows

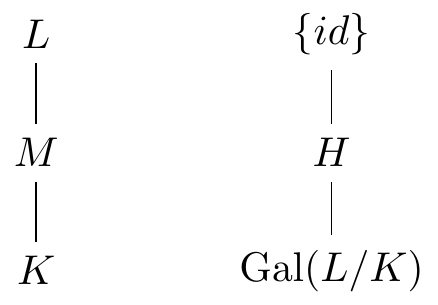
On the field side, the bigger fields are drawn higher up as usual. However, on the group side, the bigger groups are lower down and it will soon become clear why we do this. To move from intermediate fields to subgroups, we consider the $M$-automorphisms of $L$. Since $K\subset M$, these are also $K$-automorphisms so are in $\Gal(L/K)$ and it’s easy to check they form a subgroup. Furthermore, since $L/K$ is finite, normal and separable, so is $L/M$ (see Exercises 3.6 and 3.8) and hence this group is $\Gal(L/M)$. We thus have a map \[\begin{align*} \Gamma:\mathcal{F} & \longrightarrow \mathcal{G} \\ M & \longmapsto\Gal(L/M) \end{align*}\]

Remark. Note that $\Gamma$ maps $M$ to $\Gal(L/M)$, not to $\Gal(M/K)$. Both subextensions matter, but it’s not clear (or even true!) that $M/K$ is necessarily Galois or that $\Gal(M/K)$ is a subgroup of $\Gal(L/K)$. There’s no reason why $K$-automorphisms of $M$ should extend uniquely to give $K$-automorphisms of $L$. We will, however, see that under the right conditions, $\Gal(M/K)$ is a quotient of $\Gal(L/K)$ and that’s where the link between normal extensions and normal subgroups will come into play.

Something to notice is that $\Gamma$ is inclusion-reversing. The bigger the intermediate field is, the harder it is for an automorphism to fix everything in that field and, given $K\subset M_1\subset M_2\subset L$, we have $\Gal(L/M_1)\supset\Gal(L/M_2)$. This is why we draw field and group diagrams in opposite directions.

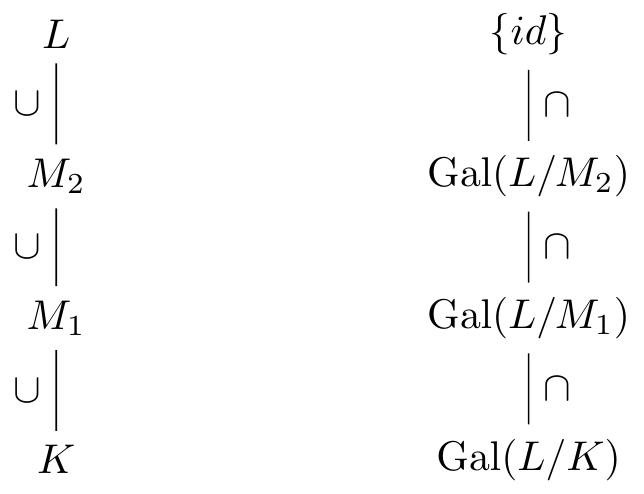
In the other direction, we construct a map from subgroups to intermediate fields via the following concept.

Definition 4.7 Let $L$ be a field and $G$ be a group of automorphisms of $L$. The fixed field $L^G$ of $G$ is the set of elements in $L$ which are invariant under all automorphisms in $G$, i.e. \[L^G=\left\{ \alpha\in L \;\mid\; \sigma(\alpha)=\alpha\;\;\text{for all $\sigma\in G$} \right\}.\]

The first important properties of fixed fields are the following:

Theorem 4.10 If $G$ is a finite group of automorphisms of $L$, then $L^G$ is a subfield of $L$ and furthermore, we have $[L:L^G]=|G|$

Proof. We will check that $L^G$ is a subfield of $L$ by showing it is closed under the field operations in $L$. Given $\alpha,\beta\in L^G$ and $\sigma\in G$,

we have $\sigma(\alpha\pm\beta)=\sigma(\alpha)\pm\sigma(\beta)=\alpha\pm\beta$ so $\alpha\pm\beta\in L^G$,
we have $\sigma(\alpha\beta)=\sigma(\alpha)\sigma(\beta)=\alpha\beta$ so $\alpha\beta\in L^G$
when $\alpha\neq 0$, we have $\sigma(\alpha^{-1})=\sigma(\alpha)^{-1}=\alpha^{-1}$ so $\alpha^{-1}\in L^G$.

To prove $[L:L^G]=|G|$, we first prove $[L:L^G]\leq |G|$, which is sometimes called Artin’s Lemma. Proving this technical result involves some quite ingenious linear algebra so don’t be too worried about completely following the details.

Let $G=\{\sigma_1,...,\sigma_n\}$ where $\sigma_1=\id$. It will suffice to show that every set $\{\alpha_1,...,\alpha_m\}\subset L$ with $m>n$ is linearly dependent over $K=L^G$. Consider the system of $n$ linear homogeneous equations in $m$ unknowns $x_1,...,x_m$: \[\begin{align*} \sigma_1(\alpha_1)x_1+\hspace{0.1em}\sigma_1(\alpha_2)x_2+\cdots+\hspace{0.1em}\sigma_1(\alpha_m)x_m &=0 \\ \sigma_2(\alpha_1)x_1+\hspace{0.1em}\sigma_2(\alpha_2)x_2+\cdots+\hspace{0.1em}\sigma_2(\alpha_m)x_m &=0 \\ \vdots\hspace{6.2em} & \tag{$\star$} \\ \sigma_n(\alpha_1)x_1+\sigma_n(\alpha_2)x_2+\cdots+\sigma_n(\alpha_m)x_m &=0 \end{align*}\] As $m>n$, we have more unknowns than equations and so there must be non-trivial solutions $(x_1,...,x_m)=(c_1,...,c_m)$ with $c_j\in L$ not all zero. Choose one having minimal number of non-zero terms $c_j$, renumber so that $c_1\neq 0$ and multiply by a non-zero scalar so that $c_1\in K^\times$. We will show that actually all $c_j\in K$ and then, since $\sigma_1=\id$, the first equation is \[\alpha_1c_1+\alpha_2c_2+\cdots+\alpha_mc_m=0,\] giving a linear relation between the $\alpha_j$ with coefficients in $K$.

If there is some $c_j\not\in K=L^G$, then $\sigma_k(c_j)\neq c_j$ for some $j\neq 1$ and $k\neq 1$. Applying $\sigma_k$ to the system of equations \[\begin{align*} \sigma_1(\alpha_1)c_1+\hspace{0.1em}\sigma_1(\alpha_2)c_2+\cdots+\hspace{0.1em}\sigma_1(\alpha_m)c_m &=0 \\ \sigma_2(\alpha_1)c_1+\hspace{0.1em}\sigma_2(\alpha_2)c_2+\cdots+\hspace{0.1em}\sigma_2(\alpha_m)c_m &=0 \\ \vdots\hspace{6em} &\\ \sigma_n(\alpha_1)c_1+\sigma_n(\alpha_2)c_2+\cdots+\sigma_n(\alpha_m)c_m &=0 \end{align*}\] and using the fact that $\{\sigma_k\sigma_1,...,\sigma_k\sigma_n\}=\{\sigma_1,...,\sigma_n\}$, we find \[\begin{align*} \sigma_1(\alpha_1)c_1+\hspace{0.1em}\sigma_1(\alpha_2)\sigma_k(c_2)+\cdots+\hspace{0.1em}\sigma_1(\alpha_m)\sigma_k(c_m) &=0 \\ \sigma_2(\alpha_1)c_1+\hspace{0.1em}\sigma_2(\alpha_2)\sigma_k(c_2)+\cdots+\hspace{0.1em}\sigma_2(\alpha_m)\sigma_k(c_m) &=0 \\ \vdots\hspace{8em} &\\ \sigma_n(\alpha_1)c_1+\sigma_n(\alpha_2)\sigma_k(c_2)+\cdots+\sigma_n(\alpha_m)\sigma_k(c_m) &=0 \end{align*}\] so $(c_1,\sigma_k(c_2),...,\sigma_k(c_m))$ is also a solution of the system $(\star)$. Subtracting this from the solution $(c_1,c_2,...,c_m)$ gives another solution with strictly more non-zero terms, contradicting the minimality condition. We conclude that $[L:L^G]\leq |G|$ as required.

Finally, since $G\subset\Aut(L/L^G)$, we have \[ [L:L^G]\leq |G| \leq \left|\Aut(L/L^G)\right|\leq [L:L^G] \] using Artin’s Lemma and Theorem 4.6. The inequalities must all be equalities and the result follows.

Corollary 4.1 If $L/K$ is a finite Galois extension, then $L^{\Gal(L/K)}=K$. Furthermore, if $L^G=K$ for some group $G$ of $K$-automorphisms of $L$, then $G=\Gal(L/K)$.

Proof. Notice that for $\sigma\in \Gal(L/K)$ we have $\sigma(a)=a$ for all $a\in K$. Hence $K$ is a subfield of $L^{\Gal(L/K)}$ and we have a tower \[K\subset L^{\Gal(L/K)}\subset L.\] Also, $L/K$ is Galois so $[L:K]=|\Gal(L/K)|$ and by the previous Theorem, we have $[L:L^{\Gal(L/K)}]=|\Gal(L/K)|$. Applying the Tower Law gives \[ [L^{\Gal(L/K)}:K]=[L:K]/[L:L^{\Gal(L/K}]=1 \] so $L^{\Gal(L/K)}=K$. Furthermore, if $L^G=K$ for some $G$, then the inclusion $G\subset\Gal(L/K)$ and the Theorem again implies $G=\Gal(L/K)$.

Remark. An immediate consequence of this is that if $L/K$ is Galois and $\alpha\in L$ but $\alpha\not\in K$, then there is an automorphism $\sigma\in\Gal(L/K)$ such that $\sigma(\alpha)\neq\alpha$.

For any subgroup $H\subset \Gal(L/K)$, we can also consider the fixed field \[L^H=\left\{ \alpha\in L \;\mid\; \sigma(\alpha)=\alpha\;\;\text{for all $\sigma\in H$} \right\}.\] This is a subfield of $L$ containing $K$ so is an intermediate field of $K\subset L^H\subset L.$ We have the following map from subgroups to intermediate fields \[\begin{align*} \Phi:\mathcal{G} & \longrightarrow \mathcal{F} \\ H & \longmapsto L^H \end{align*}\] Just like $\Gamma$, this map $\Phi$ is inclusion-reversing. Bigger subgroups produce smaller fields since it’s harder for an element in $L$ to be fixed by more automorphisms, and \[\{\id\}\subset H_1\subset H_2\subset \Gal(L/K)\quad\implies\quad L\supset L^{H_1}\supset L^{H_2}\supset K.\]

We can now state the first part of the Fundamental Theorem.

Theorem 4.11 Given a finite Galois extension $L/K$,

$\;\;\;(i)$ $\Gamma:\mathcal{F}\to\mathcal{G}$ and $\Phi:\mathcal{G}\mapsto \mathcal{F}$ are mutually inverse bijections (the Galois correspondence).

$\;\;(ii)$ For $M\in\mathcal{F}$, we have $L/M$ Galois and $|\Gal(L/M)|=[L:M]$.

$\;(iii)$ For $H\in\mathcal{G}$, we have $L/L^H$ Galois and $\Gal(L/L^H)=H$.

Proof. Suppose we have an intermediate field $K\subset M\subset L$. Since $L/K$ is Galois, it is normal and separable. This implies $L/M$ is normal and separable, hence Galois. Applying the previous Corollary to this Galois extension shows \[\Phi\circ\Gamma(M)=\Phi(\Gal(L/M)=L^{\Gal(L/M)}=M.\] On the other side, $\Gal(L/L^H)=H$ by the same Corollary and \[\Gamma\circ\Phi(H)=\Gamma(L^H)=\Gal(L/L^H)=H.\] For part $(ii)$, we already know $L/M$ is Galois so $\Gal(L/M)|=[L:M]$. For $(iii)$, by the correspondence $L/L^H$ is Galois so $[L:L^H]=|H|$ and $\Gal(L/L^H)=H$ by the previous Theorem.

Remark. Something interesting to notice is how $G=\Gal(L/K)$ acts on the set of intermediate fields $\mathcal{F}$. Given an automorphism $\sigma\in G=\Gal(L/K)$ and intermediate field $K\subset M\subset L$, consider \[\sigma(M)=\{\sigma(\alpha)\mid \alpha\in M\}.\] This is a subfield of $L$ and it contains $K$, since $\sigma$ fixes elements of $K$. Thus we have another intermediate field $K\subset\sigma(M)\subset L$ and in fact we can relate their Galois groups. They are conjugate subgroups in $\Gal(L/K)$: \[\Gal(L/\sigma(M))=\sigma\Gal(L/M)\sigma^{-1}.\] Indeed, given an automorphism $\tau:L\to L$, \[\begin{align*} \tau\in\Gal(L/\sigma(M)) &\iff \tau(\sigma(\alpha))=\sigma(\alpha)\quad\text{for all $\alpha\in M$} \\ &\iff \sigma^{-1}\tau\sigma(\alpha)=\alpha\quad\text{for all $\alpha\in M$} \\ &\iff \sigma^{-1}\tau\sigma\in\Gal(L/M) \\ &\iff \tau\in\sigma\Gal(L/M)\sigma^{-1} \end{align*}\]

The second part of the Fundamental Theorem concerns the lower extension $M/K$ in $K\subset M\subset L$. We know that $L/M$ is automatically Galois when $L/K$ is. However, $M/K$ isn’t always Galois. (Recall from the Problem sheets that $L/K$ separable implies $M/K$ separable but $L/K$ normal doesn’t imply $M/K$ normal.) So what can we do? Let $G=\Gal(L/K)$ and $H=\Gal(L/M)$ so that $H$ is a subgroup of $G$. If $M/K$ was Galois then \[|\Gal(M/K)|=[M:K]=\frac{[L:K]}{[L:M]}=\frac{|G|}{|H|}.\] This looks like $\Gal(M/K)$ is trying to be the quotient group $G/H$. But remember that quotients $G/H$ only work nicely when $H$ is a normal subgroup of $G$. We recall that a subgroup $H$ in a group $G$ is normal if and only if $g^{-1}Hg=H$ for all $g\in G$. Look back at Section 0.2.2 for further details.

Theorem 4.12 Suppose we have a finite Galois extension $L/K$ with $G=\Gal(L/K)$ and an intermediate field $K\subset M\subset L$. Then the following are equivalent:

$\;\;\;(i)$ $M/K$ is a Galois extension,

$\;\;(ii)$ $\sigma(M)=M$ for all $\sigma\in G$,

$\;(iii)$ $H=\Gal(L/M)$ is a normal subgroup of $G=\Gal(L/K)$.

Furthermore, when these conditions hold, we have $\Gal(M/K)\cong G/H$.

Proof. $(ii)\Leftrightarrow(iii)$: Using the previous remark $\sigma H\sigma^{-1}=\sigma\Gal(L/M)\sigma^{-1}=\Gal(L/\sigma(M))$ for $\sigma\in G$. Then \[\begin{align*} \text{$H$ is a normal subgroup of $G$} &\iff \sigma H\sigma^{-1}=H \quad\text{for all $\sigma\in G$} \\ &\iff \Gal(L/\sigma(M))=\Gal(L/M) \quad\text{for all $\sigma\in G$} \\ &\iff \sigma(M)=M \quad\text{for all $\sigma\in G$} \end{align*}\] by the Galois correspondence.

$(i)\Rightarrow(ii)$: Now suppose $M/K$ is Galois, hence normal. Given $\alpha\in M$ and $\sigma\in G=\Gal(L/K)$, we need to show $\sigma(\alpha)\in M$. Let $f(x)$ be the minimal polynomial of $\alpha$ over $K$. We have $f(\sigma(\alpha))=\sigma(f(\alpha))=0$ and so $\sigma(\alpha)$ is another root of $f(x)$. But $M/K$ is normal so $\sigma(\alpha)\in M$.

$(ii)\Rightarrow(i)$: Conversely, suppose $\sigma(M)=M$ for all $\sigma\in G$. The minimal polynomial $f(x)$ of $\alpha\in M$ splits over $L$ by the normality of $L/K$. Now every root of $f(x)$ in $L$ is of the form $\sigma(\alpha)$ for some $\sigma\in G$. But $\sigma(\alpha)\in\sigma(M)=M$ so every root of $f(x)$ is actually in $M$. In particular, $M/K$ is normal and it is also separable, since $L/K$ is.

Finally, suppose that $\sigma(M)=M$ for all $\sigma\in G=\Gal(L/K)$. Then the restriction $\sigma|_M$ of $\sigma$ to $M$ is a $K$-automorphism of $M$ and we have a group homomorphism \[\begin{align*} \varphi:\Gal(L/K) & \longrightarrow \Gal(M/K) \\ \sigma & \longmapsto \sigma|_M \end{align*}\] Now $\varphi$ is surjective since every automorphism $\tau\in\Gal(M/K)$ can be extended to an automorphism $\sigma\in\Gal(L/K)$ (as in the proof of Theorem 4.2). Furthermore, the kernel of $\varphi$ consists of automorphisms of $L$ with $\sigma|_M=\id_m$, i.e. $\ker(\varphi)=H=\Gal(L/M)$. Hence by the First Isomorphism Theorem for groups, we have $\Gal(M/K)\cong G/H$

Remark. Note that in the special case where a Galois extension $L/K$ has abelian Galois group $G=\Gal(L/K)$, then every subgroup $H\subset G$ is automatically normal. This means that for any intermediate extension $K\subset M\subset L$, we automatically find both subextensions $L/M$ and $M/K$ are Galois.

Example 4.6 Let $L/K$ be a normal and separable extension of prime degree $p$.

For any intermediate field $K\subset M\subset L$, the Tower Law tells us we have $[L:M]=1$ or $p$ so $M=L$ or $K$. In either case, $M$ is a normal extension of $K$.
Since $L/K$ is a Galois extension, we have $|\Gal(L/K)|=[L:K]=p$. A group of prime order is necessarily cyclic and $\Gal(L/K)\cong\mathbb{Z}/p$. By Lagrange’s Theorem, the only subgroups $H\subset\Gal(L/K)$ are $H=\{\id\}$ or $\Gal(L/K)$. In either case, $H$ is a normal subgroup of $\Gal(L/K)$.

To really understand the important results in this section and their consequences, we need to look at several more examples. We will spend the rest of the chapter (and the rest of term) doing just this.

4.5 Computations with Galois groups

4.5.1 A quadratic extension

Consider the extension $\mathbb{Q}(\sqrt{2})/\mathbb{Q}$. It is normal (every degree $2$ extension is) and separable (the characteristic is zero) so is a Galois extension. The action of any element of $\Gal(\mathbb{Q}(\sqrt{2})/\mathbb{Q})$ is determined by the image of the generator $\sqrt{2}$. We have

the identity map $\id:\sqrt{2}\mapsto\sqrt{2}$ and conjugation $\sigma:\sqrt{2}\mapsto -\sqrt{2}$.
$\sigma^2=\id$ since $\sigma^2(\sqrt{2})=\sigma(-\sqrt{2})=\sqrt{2}$.

The Galois group is $G=\Gal(\mathbb{Q}(\sqrt{2})/\mathbb{Q})=\{\id,\sigma\}\cong \mathbb{Z}/2$ and the only subgroups of $G$ are $G$ itself and the trivial group:

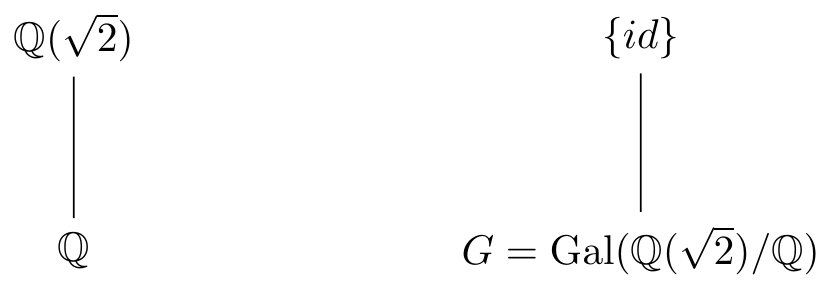
Remark. More generally, given a field $K$ with $\ch(K)\neq 2$ and an element $a\in K^\times$ with $a\not\in{K^\times}^2$, we have an extension $L=K(\sqrt{a})$ over $K$. It is normal since $[L:K]=2$, and is separable since either $\ch(K)=0$ or $\ch(K)=p$ and $p\nmid [L:K]$. Everything is the same as above. We have $\sigma(\sqrt{a})=-\sqrt{a}$ and \[\Gal(L/K)=\{\id,\sigma\}\cong\mathbb{Z}/2.\]

4.5.2 A biquadratic extension

Consider the extension $L=\mathbb{Q}(\sqrt{2},\sqrt{3})$ over $\mathbb{Q}$. It is normal (it’s the splitting field of $(x^2-2)(x^2-3)$ over $\mathbb{Q}$) and separable (the characteristic is zero) so is a Galois extension.

Let’s forget that we know $[L:\mathbb{Q}]=4$ and prove it again using our new knowledge of Galois Theory:

Suppose $\sqrt{3}\in\mathbb{Q}(\sqrt{2})$ so that $L=\mathbb{Q}(\sqrt{2})$.
We have $\Gal(\mathbb{Q}(\sqrt{2})/\mathbb{Q})=\{\id,\sigma\}$ as in the previous example, where $\sigma(\sqrt{2})=-\sqrt{2}$. Then \[\sigma(\sqrt{3})^2=\sigma(3)=3\quad\implies\quad \sigma(\sqrt{3})=\pm\sqrt{3}.\]
If $\sigma(\sqrt{3})=\sqrt{3}$, then $\sqrt{3}\in\mathbb{Q}(\sqrt{2})^{\{\id,\sigma\}}=\mathbb{Q}$.
If $\sigma(\sqrt{3})=-\sqrt{3}$, then $\sigma(\sqrt{6})=\sigma(\sqrt{2})\sigma(\sqrt{3})=(-\sqrt{2})(-\sqrt{3})=\sqrt{6}$ so $\sqrt{6}\in\mathbb{Q}(\sqrt{2})^{\{\id,\sigma\}}=\mathbb{Q}$.
Thus we have either $\sqrt{3}$ or $\sqrt{6}$ in $\mathbb{Q}$ which we know is false. In particular, $\sqrt{3}\not\in\mathbb{Q}(\sqrt{2})$ and \[[L:\mathbb{Q}]=[L:\mathbb{Q}(\sqrt{2})] [\mathbb{Q}(\sqrt{2}):\mathbb{Q}]=4.\]

Now that we know $G=\Gal(L/\mathbb{Q})$ has order $[L:\mathbb{Q}]=4$, let’s determine its structure. Any group of order $4$ is isomorphic to $\mathbb{Z}/4$ or $\mathbb{Z}/2\times\mathbb{Z}/2$, so which is it?

For any $\varphi\in G$, we have \[\begin{cases}\;\;\varphi(\sqrt{2})^2=\varphi(2)=2 \\ \;\;\varphi(\sqrt{3})^2=\varphi(3)=3\end{cases} \quad\implies\quad \begin{cases}\;\;\varphi(\sqrt{2})=\pm\sqrt{2} \\ \;\;\varphi(\sqrt{3})=\pm\sqrt{3}\end{cases}\] The two choices of $\pm$ signs determine $\varphi$ completely. Furthermore, these four possibilities will give us each of the $|G|=[L:\mathbb{Q}]=4$ distinct $\mathbb{Q}$-automorphisms of $L$. Explicitly, we have $G=\{\id,\sigma,\tau,\sigma\tau\}$ where

$\id\in G$ is given by $\id(\sqrt{2})=\sqrt{2}\;$ and $\id(\sqrt{3})=\sqrt{3}$.
$\sigma\in G$ is given by $\sigma(\sqrt{2})=-\sqrt{2}$ and $\sigma(\sqrt{3})=\sqrt{3}$.
$\tau\in G$ is given by $\tau(\sqrt{2})=\sqrt{2}\;\;\;$ and $\tau(\sqrt{3})=-\sqrt{3}$.
The composition $\sigma\tau\in G$ satisfies $\sigma\tau(\sqrt{2})=-\sqrt{2}$ and $\sigma\tau(\sqrt{3})=-\sqrt{3}$.

Notice that $\sigma^2=\tau^2=(\sigma\tau)^2=\id$ and $\sigma\tau=\tau\sigma$. The three order $2$ elements generate cyclic subgroups of order $2$ in $G$: \[H_1=\langle\sigma\rangle=\{\id,\sigma\},\quad H_2=\langle\tau\rangle=\{\id,\tau\},\quad H_3=\langle\sigma\tau\rangle=\{\id,\sigma\tau\}\] and furthermore, these are the only proper subgroups of $G$. In particular, we have \[G=\langle\sigma,\tau\rangle=\langle\sigma\rangle\times\langle\tau\rangle\cong \mathbb{Z}/2\times\mathbb{Z}/2\] and the subgroups fit together as follows:

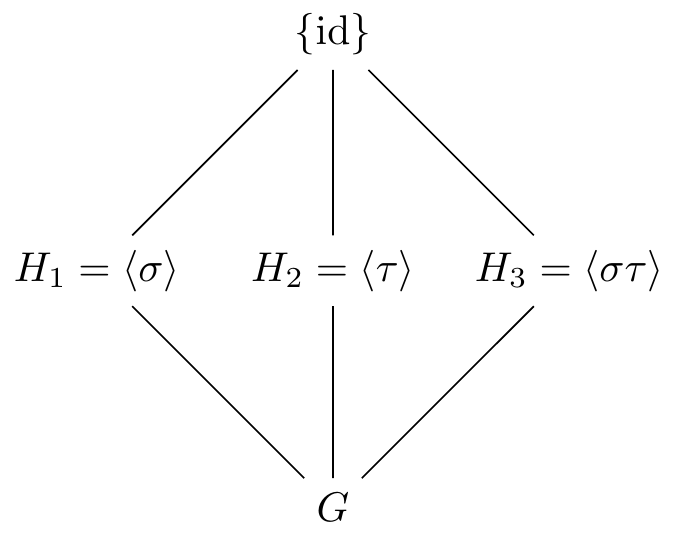
The Galois correspondence tells us the intermediate fields in $L/\mathbb{Q}$ are the fixed fields of these subgroups. Notice that $\sigma(\sqrt{3})=\sqrt{3}$ so $\mathbb{Q}(\sqrt{3})\subset L^{H_1}$. But by the Fundamental Theorem, \[ [L:\mathbb{Q}(\sqrt{3})]=2=|H_1|=[L:L^{H_1}] \quad\implies\quad L^{H_1}=\mathbb{Q}(\sqrt{3})\] Similarly we find $L^{H_2}=\mathbb{Q}(\sqrt{2})$. For $L^{H_3}$, notice $\sigma\tau(\sqrt{6})=\sigma\tau(\sqrt{2})\sigma\tau(\sqrt{3})=(-\sqrt{2})(-\sqrt{3})=\sqrt{6}$ so we get $L^{H_3}=\mathbb{Q}(\sqrt{6})$. The intermediate fields fit together as follows:

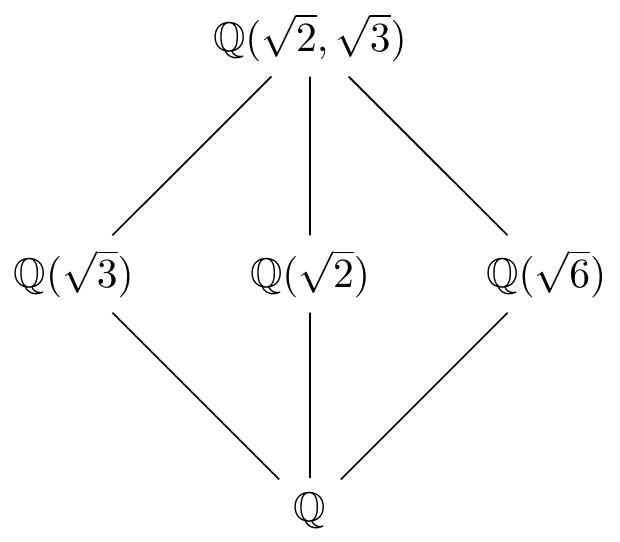
Remark. We can generalise the above to arbitrary base fields $K$ with $\ch(K)\neq 2$ and other square roots. Given $a,b\in K^\times$ with $a,b\not\in {K^\times}^2$, notice that it is not generally true that $[K(\sqrt{a},\sqrt{b}):K]=4$. For instance, we have $\mathbb{Q}(\sqrt{2},\sqrt{8})=\mathbb{Q}(\sqrt{2})$ so $[\mathbb{Q}(\sqrt{2},\sqrt{8}):\mathbb{Q}]=2$.

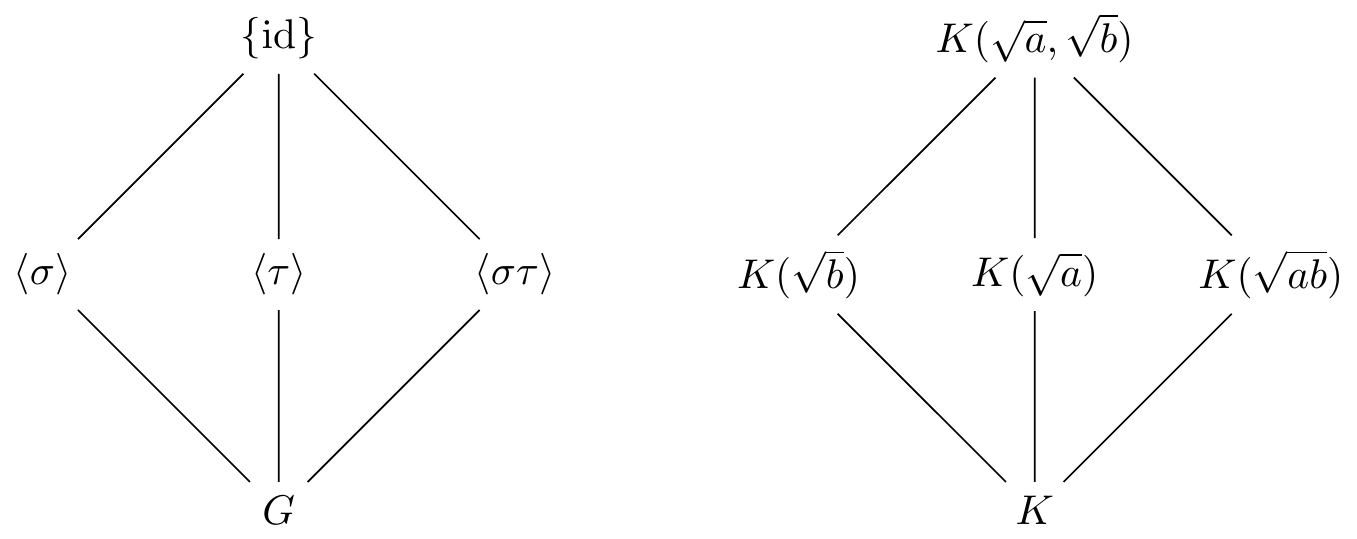
However, if $a,b$ and $ab\not\in {K^\times}^2$, then we will have $[K(\sqrt{a},\sqrt{b}):K]=4$ and can follow the same strategy as with $\mathbb{Q}(\sqrt{2},\sqrt{3})/\mathbb{Q}$. One defines automorphisms by

$\sigma(\sqrt{a})=-\sqrt{a}$, $\;\sigma(\sqrt{b})=\sqrt{b}\;$ and $\;\tau(\sqrt{a})=\sqrt{a}$, $\;\tau(\sqrt{b})=-\sqrt{b}$,
Then $\sigma^2=\tau^2=(\sigma\tau)^2=\id\;$ and $\;\sigma\tau=\tau\sigma$,
The Galois group is $\Gal(K(\sqrt{a},\sqrt{b})/K)=\langle\,\sigma\,\rangle\times\langle\,\tau\,\rangle\cong\,\mathbb{Z}/2\times\mathbb{Z}/2$.

4.5.3 A degree $8$ extension

Let’s do something similar and find the structure of the Galois group of $L=\mathbb{Q}(\sqrt{2},\sqrt{3},\sqrt{5})$ over $\mathbb{Q}$. This is a Galois extension since it’s the splitting field of $(x^2-2)(x^2-3)(x^2-5)$ over the characteristic zero field $\mathbb{Q}$. First we find its degree using the subfield $M=\mathbb{Q}(\sqrt{2},\sqrt{3})$ and the Galois group constructed earlier: \[\Gal(M/\mathbb{Q})=\langle\,\sigma\,\rangle\times\langle\,\tau\,\rangle\] where $\sigma(\sqrt{2})=-\sqrt{2}$, $\sigma(\sqrt{3})=\sqrt{3}$ and $\tau(\sqrt{2})=\sqrt{2}$, $\tau(\sqrt{3})=-\sqrt{3}$.

Suppose $\sqrt{5}\in M$. Notice we have $\sigma(\sqrt{5})=\pm\sqrt{5}$ and $\tau(\sqrt{5})=\pm\sqrt{5}$. We’ll show each of the four choices of signs creates an irrational number in $M^{\langle\,\sigma,\tau\,\rangle}=\mathbb{Q}$. First consider how $\sigma$ acts on $\sqrt{5}$: \[\begin{align*} \sigma(\sqrt{5})&=\sqrt{5}\;\;\Rightarrow\;\;\sqrt{5}\in M^{\langle\,\sigma\,\rangle}=\mathbb{Q}(\sqrt{3}) \\ \sigma(\sqrt{5})&=-\sqrt{5}\;\;\Rightarrow\;\;\sigma(\sqrt{10})=\sigma(\sqrt{2})\sigma(\sqrt{5})=\sqrt{10} \;\;\Rightarrow\;\;\sqrt{10}\in M^{\langle\,\sigma\,\rangle}=\mathbb{Q}(\sqrt{3}). \end{align*}\]
Suppose $\sqrt{5}\in M^{\langle\,\sigma\,\rangle}=\mathbb{Q}(\sqrt{3})$. Then \[\begin{align*} \tau(\sqrt{5})&=\sqrt{5}\;\;\Rightarrow\;\;\sqrt{5}\in M^{\langle\,\sigma,\tau\,\rangle}=\mathbb{Q} \\ \tau(\sqrt{5})&=-\sqrt{5}\;\;\Rightarrow\;\;\tau(\sqrt{15})=\tau(\sqrt{3})\tau(\sqrt{5})=\sqrt{15} \;\;\Rightarrow\;\;\sqrt{15}\in M^{\langle\,\sigma,\tau\,\rangle}=\mathbb{Q}. \end{align*}\] Suppose $\sqrt{10}\in M^{\langle\,\sigma\,\rangle}=\mathbb{Q}(\sqrt{3})$. Then $\sqrt{30}=\sqrt{3}\sqrt{10}\in M^{\langle\,\sigma\,\rangle}$ and \[\begin{align*} \tau(\sqrt{5})&=\sqrt{5}\;\;\Rightarrow\;\;\tau(\sqrt{10})=\tau(\sqrt{2})\tau(\sqrt{5})=\sqrt{10} \;\;\Rightarrow\;\;\sqrt{10}\in M^{\langle\,\sigma,\tau\,\rangle}=\mathbb{Q} \\ \tau(\sqrt{5})&=-\sqrt{5}\;\;\Rightarrow\;\;\tau(\sqrt{30})=\tau(\sqrt{2})\tau(\sqrt{3})\tau(\sqrt{5})=\sqrt{30} \;\;\Rightarrow\;\;\sqrt{30}\in M^{\langle\,\sigma,\tau\,\rangle}=\mathbb{Q}. \end{align*}\]
We’ve found that one of $\sqrt{5},\sqrt{10},\sqrt{15},\sqrt{30}$ is in $\mathbb{Q}$ which we know is false. Hence $\sqrt{5}\not\in M$ and we have \[[L:\mathbb{Q}]=[L:M] [M:\mathbb{Q}]=8.\]

To find the Galois group, $G=\Gal(L/\mathbb{Q})$, we need to write down $8$ distinct elements. They will be determined by the choices of $\sqrt{2}\mapsto\pm\sqrt{2}$, $\sqrt{3}\mapsto\pm\sqrt{3}$, $\sqrt{5}\mapsto\pm\sqrt{5}$ and we can define them as follows:

The quadratic extension $L/\mathbb{Q}(\sqrt{3},\sqrt{5})$ gives $\sigma_1\in G$ where \[\sigma_1(\sqrt{2})=-\sqrt{2},\quad\sigma_1(\sqrt{3})=\sqrt{3},\quad\sigma_1(\sqrt{5})=\sqrt{5}\]
The quadratic extension $L/\mathbb{Q}(\sqrt{2},\sqrt{5})$ gives $\sigma_2\in G$ where \[\sigma_2(\sqrt{2})=\sqrt{2},\quad\sigma_2(\sqrt{3})=-\sqrt{3},\quad\sigma_2(\sqrt{5})=\sqrt{5}\]
The quadratic extension $L/\mathbb{Q}(\sqrt{2},\sqrt{3})$ gives $\sigma_3\in G$ where \[\sigma_3(\sqrt{2})=\sqrt{2},\quad\sigma_3(\sqrt{3})=\sqrt{3},\quad\sigma_3(\sqrt{5})=-\sqrt{5}\]

These satisfy $\sigma_i^2=\id$ and $\sigma_i\sigma_j=\sigma_j\sigma_i$ for $1\leq i,j\leq 3$. The various products produce the required $8$ distinct elements \[\begin{align*} \Gal(L/\mathbb{Q})&=\left\{\id,\sigma_1,\sigma_2,\sigma_3,\sigma_1\sigma_2,\sigma_1\sigma_3,\sigma_2\sigma_3,\sigma_1\sigma_2\sigma_3\right\} \\ &=\langle\,\sigma_1\,\rangle\times\langle\,\sigma_2\,\rangle\times\langle\,\sigma_3\,\rangle \\ &\cong\mathbb{Z}/2\times\mathbb{Z}/2\times\mathbb{Z}/2. \end{align*}\] How about the subgroups and intermediate fields? There are $7$ subgroups of order $2$ in $G$ and these have corresponding fixed fields of degree $4$ over $\mathbb{Q}$:

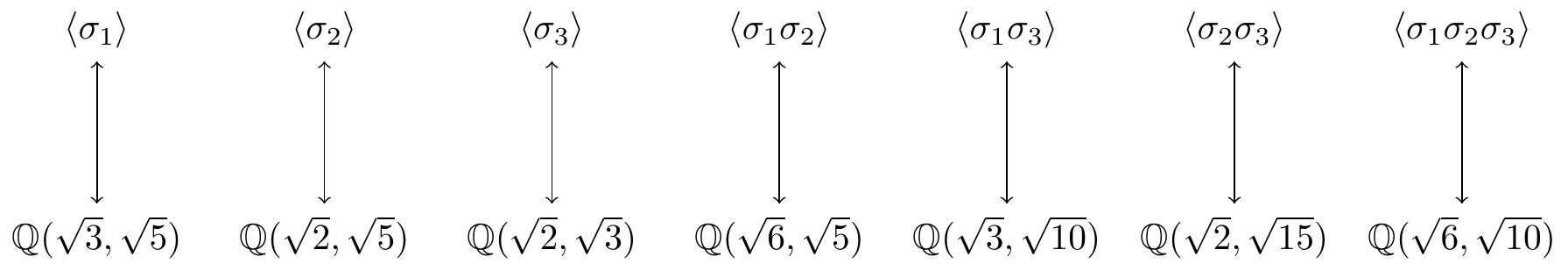
There are $7$ subgroups of order $4$ in $G$ and these have corresponding fixed fields of degree $2$ over $\mathbb{Q}$:

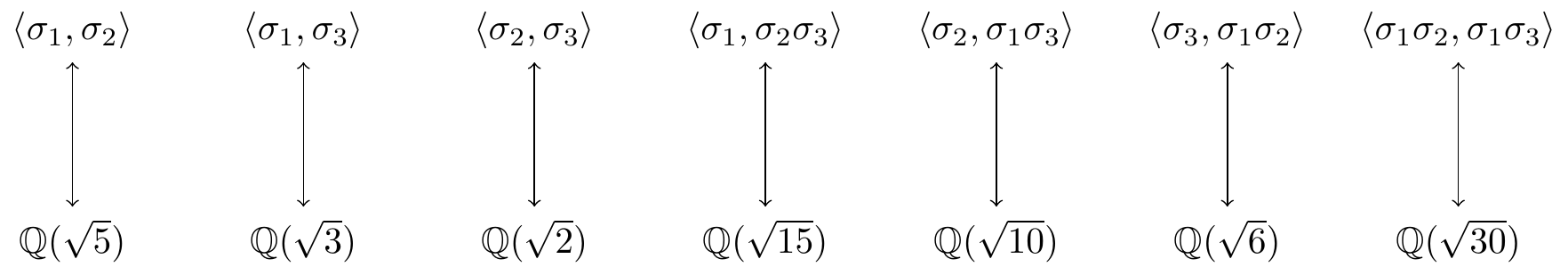
Drawing the full subgroup/subfield diagrams is possible but is a bit of a mess. Each subgroup of order $2$ is contained in three subgroups of order $4$ and we get a cobweb of inclusions…

4.5.4 A cubic extension and its normal closure

Let $L=\mathbb{Q}(\theta)$ where $\theta$ is a root of $x^3-2\in\mathbb{Q}[x]$. This isn’t a Galois extension since it isn’t normal. However, we can embed it in its normal closure \[N=\mathbb{Q}(\theta,\omega)=\mathbb{Q}(\theta,\sqrt{-3})\] where as usual, $\omega=e^{2\pi i/3}=(-1+\sqrt{-3})/2$. Let $M=\mathbb{Q}(\omega)$ so that $[M:\mathbb{Q}]=2$. We also have $[L:\mathbb{Q}]=3$, $[N:\mathbb{Q}]=6$ and the familiar diagram

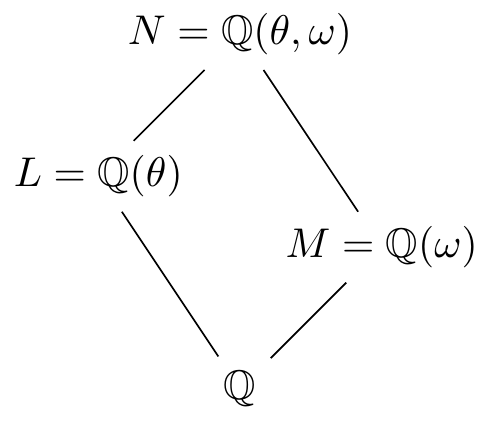
The extension $N/\mathbb{Q}$ is Galois so let’s determine the structure of its Galois Group $G=\Gal(N/\mathbb{Q})$. Since it has order $|G|=[N:\mathbb{Q}]=6$, we know that $G$ must be isomorphic to either the cyclic group $\mathbb{Z}/6$ or the symmetric group $S_3$ (which is the same as the dihedral group $D_3$). Now,

$G$ contains the subgroup $\Gal(N/L)$. As $N=L(\omega)=L(\sqrt{-3})$ is a quadratic extension, we can describe this easily: \[\Gal(N/L)=\{\id,\tau\}=\langle\,\tau\rangle\cong\mathbb{Z}/2\] where $\tau(\sqrt{-3})=-\sqrt{-3}$, or equivalently, $\tau(\omega)=\omega^2$. Also note that $\tau(\theta)=\theta$ as $\theta\in L$.
$G$ contains the subgroup $H=\Gal(N/M)$. This has order $[N:M]=3$ so is a cyclic group of order $3$ and we can describe it as \[H=\Gal(N/M)=\{\id,\sigma,\sigma^2\}=\langle\,\sigma\,\rangle\cong\mathbb{Z}/3\] where $\sigma(\theta)=\omega\theta$. Also note that $\sigma(\omega)=\omega$ as $\omega\in M$ and $\sigma^2(\theta)=\sigma(\omega\theta)=\omega^2\theta$. In particular, $H$ is permuting the three roots of $x^3-2$.

Clearly, $\tau\not\in H$ and there are disjoint cosets $H=\{\id,\sigma,\sigma^2\}$ and $\tau H=\{\tau,\tau\sigma,\tau\sigma^2\}$ in $G$. Thus we have $|G|=6$ elements (each having a different image of the pair $\theta$, $\omega$) \[G=H\cup \tau H=\{\id,\sigma,\sigma^2,\tau,\tau\sigma,\tau\sigma^2\}.\] Furthermore, notice \[\sigma\tau(\omega)=\sigma(\omega^2)=\omega^2=\tau(\omega)=\tau\sigma^2(\omega),\] \[\sigma\tau(\theta)=\sigma(\theta)=\omega\theta=\tau(\omega^2\theta)=\tau\sigma^2(\theta).\] The generators $\tau$ and $\sigma$ in $G$ satisfy the relations $\tau^2=\sigma^3=\id$ and $\sigma\tau=\tau\sigma^2$. That means $G$ is isomorphic to the non-abelian group $S_3\cong D_3$ of order $6$.

Now consider the subgroups of $G$ and corresponding intermediate fields in $N/\mathbb{Q}$.

There is only one subgroup of order $3$, namely $H=\langle\,\sigma\,\rangle$ and the fixed field is $N^{\langle\,\sigma\,\rangle}=M=\mathbb{Q}(\omega)$. Also, note that $H$ is the only proper normal subgroup in $G$. Correspondingly, $M$ is the only normal extension of $\mathbb{Q}$ in $N$.
The elements $\tau$, $\tau\sigma$ and $\tau\sigma^2$ have order $2$ and we have three cyclic subgroups of order $2$ in $G$, namely $\langle\,\tau\,\rangle$, $\langle\,\tau\sigma\,\rangle$ and $\langle\,\tau\sigma^2\,\rangle$. The corresponding fixed fields are \[N^{\langle\,\tau\,\rangle}=\mathbb{Q}(\theta),\qquad N^{\langle\,\tau\sigma\,\rangle}=\mathbb{Q}(\omega\theta),\qquad N^{\langle\,\tau\sigma^2\,\rangle}=\mathbb{Q}(\omega^2\theta).\] These three subgroups are not normal in $G$ and their fixed fields are not normal extensions of $\mathbb{Q}$. Notice that these intermediate fields are precisely $L$, $\sigma(L)$ and $\sigma^2(L)$.

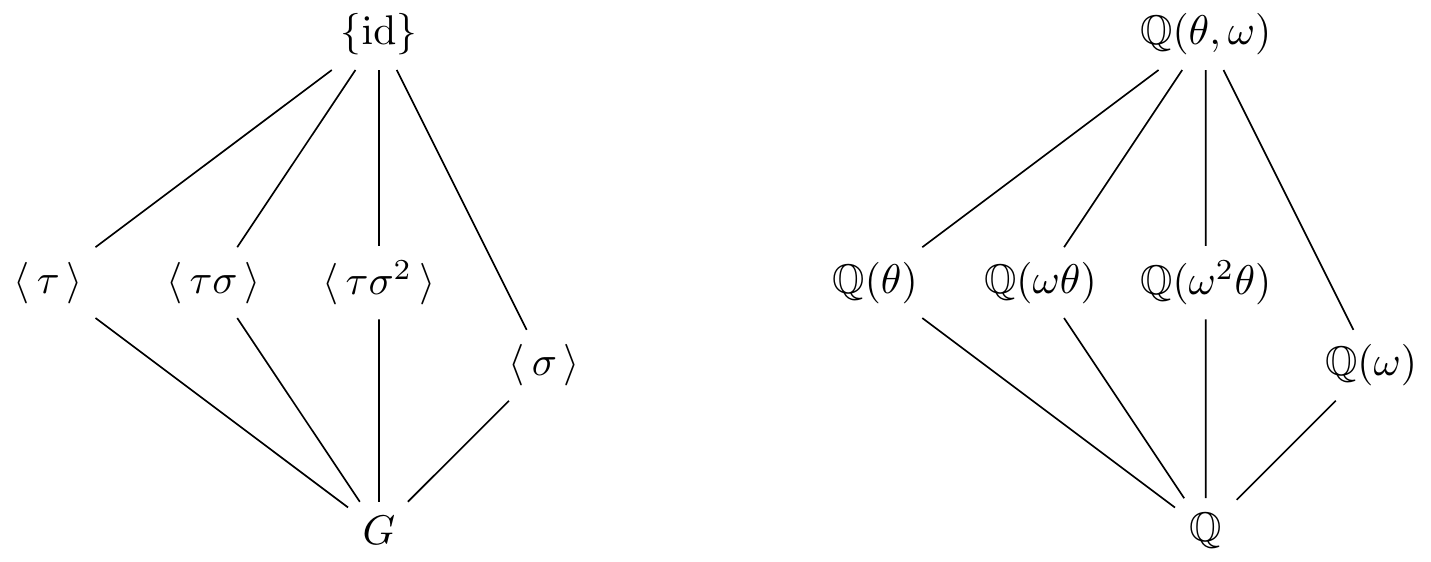
Here’s an exercise using the above Galois Theory to prove something we should already expect.

Example 4.7 Let’s show that $\sqrt[3]{3}\not\in\mathbb{Q}(\sqrt[3]{2})$ by considering fields and automorphisms.

Suppose on the contrary, that $\sqrt[3]{3}\in\mathbb{Q}(\sqrt[3]{2})$. Then $\sqrt[3]{3}$ is in the normal closure $\mathbb{Q}(\omega,\sqrt[3]{2})$. As above, we have $\sigma\in\Gal(N/\mathbb{Q})$ with $\sigma(\sqrt[3]{2})=\omega\sqrt[3]{2}$ and $N^{\langle\,\sigma\,\rangle}=\mathbb{Q}(\omega)$. Also, \[\sigma(\sqrt[3]{3})^3=\sigma(3)=3\quad\implies\quad \sigma(\sqrt[3]{3})=\sqrt[3]{3},\; \omega\sqrt[3]{3}\;\text{or}\;\omega^2\sqrt[3]{3}. \]

If $\sigma(\sqrt[3]{3})=\sqrt[3]{3}$ then $\sqrt[3]{3}\in \mathbb{Q}(\omega)$ and so \[\mathbb{Q}(\sqrt[3]{3})\subset N^{\langle\,\sigma\,\rangle}=\mathbb{Q}(\omega).\]
If $\sigma(\sqrt[3]{3})=\omega\sqrt[3]{3}$ then $\sigma(\sqrt[3]{3/2})=(\omega\sqrt[3]{3})/(\omega\sqrt[3]{2})=\sqrt[3]{3/2}$ and so \[\mathbb{Q}(\sqrt[3]{3/2})=\mathbb{Q}(\sqrt[3]{12})\subset N^{\langle\,\sigma\,\rangle}=\mathbb{Q}(\omega).\]
If $\sigma(\sqrt[3]{3})=\omega^2\sqrt[3]{3}$ then $\sigma(\sqrt[3]{3/4})=(\omega^2\sqrt[3]{3})/(\omega^2\sqrt[3]{4})=\sqrt[3]{3/4}$ and so \[\mathbb{Q}(\sqrt[3]{3/4})=\mathbb{Q}(\sqrt[3]{6})\subset N^{\langle\,\sigma\,\rangle}=\mathbb{Q}(\omega).\]

In each case, we find a degree $3$ extension $\mathbb{Q}(\sqrt[3]{m})$ of $\mathbb{Q}$ contained in a degree $2$ extension $\mathbb{Q}(\omega)/\mathbb{Q}$ which is impossible.

Remark. We can examine the isomorphism $G=\Gal(N/\mathbb{Q})\cong S_3$ from the perspective of the roots $\theta_1=\sqrt[3]{2}$, $\theta_2=\omega\sqrt[3]{2}$ and $\theta_3=\omega^2\sqrt[3]{2}$ of $x^3-2\in\mathbb{Q}[x]$ in the splitting field \[N=\mathbb{Q}(\theta_1,\theta_2,\theta_3)=\mathbb{Q}(\sqrt[3]{2},\omega).\]

In fact, if we plot the roots in the complex plane, we have the symmetry group $S_3\cong D_3$ of an equilateral triangle.

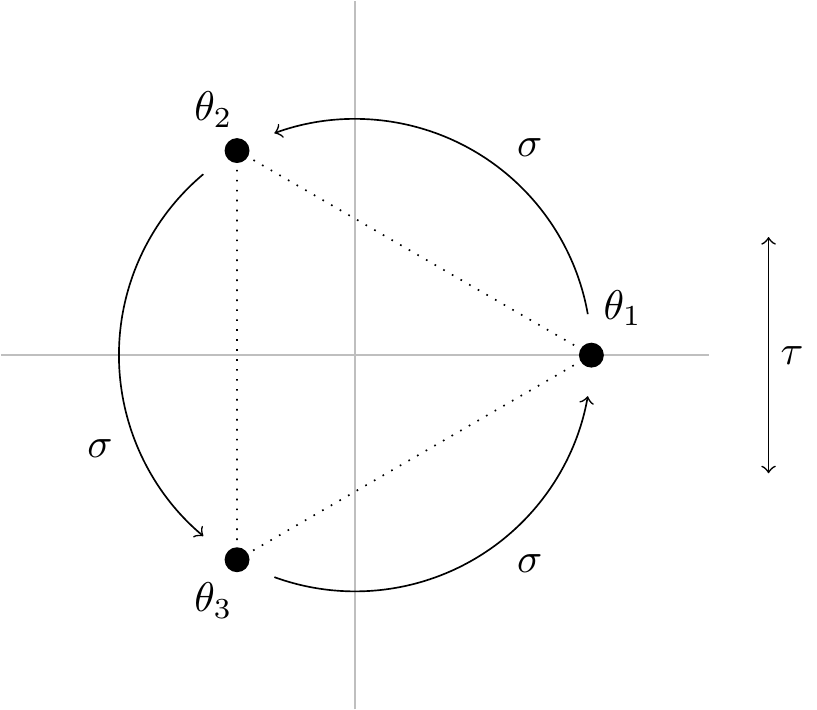
Note, whilst $\tau$ does reflect elements of $N\subset\mathbb{C}$, the other automorphism $\sigma$ doesn’t rotate $N$, it only rotates the roots. Indeed, elements of $\mathbb{Q}\subset N\subset\mathbb{C}$ are fixed by $\sigma$.

For $g\in G=\langle\,\sigma,\tau\,\rangle$, we have $\{g(\theta_1),g(\theta_2),g(\theta_3)\}=\{\theta_1,\theta_2,\theta_3\}$, i.e. $g$ permutes the three roots. Thus $g$ gives a permutation $\pi\in S_3$ where $g(\theta_i)=\theta_{\pi(i)}$ and we have a map \[\begin{align*} \varphi\;:\; G &\longrightarrow \,S_3 \\ g &\longmapsto \pi \end{align*}\] The group operation in $G$ is given by composing field automorphisms and the group operation in $S_3$ is given by composing permutations. These are compatible and $\varphi$ is a group homomorphism. The kernel of $\varphi$ consists of $g\in G$ such that $g(\theta_i)=\theta_i$ for $i=1,2,3$ and therefore is trivial. As a result, this group homomorphism $\varphi$ is an injection. However, the two groups $G$ and $S_3$ have the same order and so $\varphi$ is an isomorphism.

More generally, given a polynomial $f(x)\in K[x]$ of degree $n\geq 1$, we define the Galois group of $f(x)$ to be Galois group of the splitting field of $f(x)$ over $K$ (provided this is separable). Elements of this group give certain permutations of the roots of $f(x)$ and the Galois group of $f(x)$ can be embedded in the symmetric group $S_n$. We thus have a general pattern \[\text{polynomial}\;\;\longmapsto\;\;\text{field extension}\;\;\longmapsto\;\;\text{permutation group} \] In Galois’ original formulation of the Theory, he managed this by going straight from polynomials to groups. The modern approach involving field extensions both simplifies and generalises this.

To test your understanding, a very instructive example illustrating all the ideas from this chapter is Exercise 4.3, which investigates the Galois group of the splitting field of $x^4-5$ over $\mathbb{Q}$.

Galois Theory III (MATH3041)