Background Material from Algebra II

Galois Theory is a very algebraic subject and we will make extensive use of many of the important concepts from Algebra II. We’ll take the same slightly odd approach of discussing rings before groups (even though the definition of a ring uses groups!) as we will require the ring theory first in our course.

0.1 Rings and polynomials

0.1.1 The concept of a ring

Recall the definition of a ring from Algebra II. In this course, our rings will always be commutative and unital. That means when we say “ring”, the multiplication is commutative and there is a multiplicative identity (though we don’t assume multiplicative inverses). The full formal definition is as follows.

Definition 0.1 A ring is a set $R$ with two binary operations “addition” $+_R$ and “multiplication” $\cdot_R$ which satisfy the following properties.

$(1)$ The set $R$ is an abelian group under addition $+_R$, i.e.

$\quad\;\;$(associativity): $(a+_Rb)+_Rc=a+_R(b+_Rc)$ for any $a, b, c\in R$,

$\quad\;\;$(commutativity): $a+_Rb=b+_Ra$ for any $a, b\in R$,

$\quad\;\;$(identity): there exists an additive identity $0_R\in R$ such that $a+_R0_R=a$ for all $a\in R$,

$\quad\;\;$(inverses): every element $a\in R$ has an additive inverse $a'\in R$ such that $a+_Ra'=0_R$.

$(2)$ The set $R$ is “almost” an abelian group under multiplication $\cdot_R$, i.e.

$\quad\;\;$(associativity): $(a\cdot_R b)\cdot_Rc=a\cdot_R(b\cdot_R c)$ for any $a, b, c\in R$,

$\quad\;\;$(commutativity): $a\cdot_R b=b\cdot_R a$ for any $a, b\in R$,

$\quad\;\;$(identity): there exists a multiplicative identity $1_R\in R$ such that $a\cdot_R 1_R=a$ for all $a\in R$

$(3)$ The two operations are compatible with brackets, i.e.

$\quad\;\;$(distributivity): $a\cdot_R(b+_Rc)=a\cdot_R b+_Ra\cdot_R c$.

Remark. It can be easily proved from the above definition that:

there can be only one additive identity $0_R\in R$ and only one multiplicative identity $1_R\in R$,
the additive inverse of an element $a\in R$ is uniquely determined and we denote it by $-a$,
for any $a\in R$, we have $0_R\cdot_R a=0_R$, $1_R\cdot_R a=a$ and $(-1_R)\cdot_Ra=-a$.

Now that we’ve got this precise definition out of the way, we remark that almost all of the time, the ring we are working in will be clear from the context. To save ink and notation overload, we’ll often forget to write the subscripts on the symbols $+_R$, $\cdot_R$, $0_R$, $1_R$. In fact, the multiplication symbol is often omitted completely and we’ll just write $ab$ to mean $a\cdot_R b$.

Example 0.1 We should already be familiar with many rings:

The ring of integers $\mathbb{Z}$,
The ring of rational numbers $\mathbb{Q}$,
The ring of real numbers $\mathbb{R}$,
The ring of Gaussian integers $\mathbb{Z}[i]=\left\{a+bi\;|\;a,b\in\mathbb{Z}\right\}$,
The ring of complex numbers $\mathbb{C}=\left\{a+bi\;|\;a,b\in\mathbb{R}\right\}$,
The finite ring $\mathbb{Z}/n$ of integers modulo $n$ for a given $n\in\mathbb{N}$.
The trivial ring $\{0\}$. This is a strange one, not least because we must have $1=0$. In fact, this is the only ring with $1=0$. (Can you prove this?)

0.1.2 New rings from old

Given some rings we know about, there are various ways to create new ones, such as

$(a)$ Subrings: Given a ring $R$, a subring is a subset $S\subset R$ which is itself a ring with the addition and multiplication induced from $R$. Note that since our definition of a ring includes the existence of $1_R\in R$, we demand that $S$ has the same multiplicative identity, i.e. $1_R\in S$.

$(b)$ Direct products: Given rings $R$ and $S$, we can form the direct product $R\times S$ consisting of all pairs $(r,s)$ with $r\in R$ and $s\in S$. This can be given the structure of a ring by letting addition and multiplication act component-wise: \[\begin{align*} &(r_1,s_1)+_{R\times S}(r_2,s_2)=(r_1+_Rr_2,s_1+_Ss_2) \\ \text{and}\;\;\; &(r_1,s_1)\cdot_{R\times S}(r_2,s_2)=(r_1\cdot_Rr_2,s_1\cdot_Ss_2) \end{align*}\] Note the additive identity is $(0_R,0_S)$ and the multiplicative identity is $(1_R,1_S)$. You should be able to see how to extend the definition naturally for a product of a finite number of rings.

$(c)$ Ring-valued functions: Given a set $S$ and a ring $R$, we write $\Map(S,R)$ for the set of all functions $f:S\to R$. This can be given the structure of a ring by using the operations \[(f+g)(s)=f(s)+g(s)\quad\text{and}\quad (fg)(s)=f(s)g(s)\quad\text{for all $s\in S$.} \]

$(d)$ Polynomial rings: Given a ring $R$, we can form the ring of polynomials $R[x]$ with coefficients in $R$ and a variable $x$. This is the set \[\left\{a_nx^n+\cdots+a_1x+a_0 \;|\; a_i\in R,\; n\in\mathbb{N}_0\right\}\] together with the obvious addition and multiplication.

For a polynomial $f(x)=a_nx^n+\cdots+a_1x+a_0$ with $a_n\neq 0$, the degree of $f(x)$ is $\deg f(x)=n$. We call this $a_n\neq 0$ the leading coefficient and $f(x)$ is monic if its leading coefficient is $1$.

There is also the zero polynomial $f(x)=0$ having all coefficients equal to zero and we set $\deg(0)=-\infty$.

0.1.3 Integral domains and fields

A field is an especially nice ring where division works as well as you could expect and these will be central objects in Galois Theory.

Definition 0.2 An element $a$ in a ring $R$ is called

$(1)$ a zero divisor if there is a non-zero $b\in R$ such that $ab=0$.

$(2)$ a unit if there is $b\in R$ such that $ab=1$. (We say these elements are invertible.)

We will use the notation $R^\times$ for the subset of invertible elements. These are also called the units in $R$. Try to prove this subset always forms a group under multiplication (or look back at Algebra II notes). In particular, the multiplicative inverse of any $a\in R^\times$ is unique and we write it as $a^{-1}$.

Definition 0.3 A ring $R$ is called

$(1)$ an integral domain if $1\neq 0$ and there are no zero divisors in $R\setminus\{0\}$.

$(2)$ a field if $1\neq 0$ and each non-zero element $a\in R\setminus \{0\}$ is invertible, i.e. $R^\times=R\setminus\{0\}$.

An immediate consequence is that fields are always integral domains. To see this, notice if $a\neq 0$ was a zero divisor in a field, then there is $b\neq 0$ such that $ab=0$ and $c$ such that $ac=1$. But then we have $b=b(ac)=(ab)c=0$ contradicting $b\neq 0$.

Example 0.2 $(a)$ The rings $\mathbb{Z}$, $\mathbb{Q}$, $\mathbb{R}$ and $\mathbb{C}$ are all integral domains. Furthermore, they are all fields except for $\mathbb{Z}$ which has non-invertible elements, e.g. $2\in\mathbb{Z}$ is not invertible in $\mathbb{Z}$. Similarly, $\mathbb{Z}[i]$ is an integral domain but isn’t a field (as again, e.g. $2$ is not invertible).

$(b)$ The direct product $\mathbb{Z}\times\mathbb{Z}$ is not an integral domain. It has non-trivial zero divisors, such as \[(1,0)\cdot(0,1)=(0,0).\] Perhaps you can identify all the zero divisors in this ring?

In a similar way, a direct product of fields is not a field since it contains non-trivial zero divisors so isn’t even an integral domain.

$(c)$ The ring $\mathbb{Z}/n$ is an integral domain (and in fact is a field) if and only if $n$ is prime. One way is easy: if $n$ is not prime, say $n=ab$ with $1<a,b<n$, then we get zero divisors. For the other way, we can use the extended Euclidean algorithm (see the Algebra II notes). When considering the ring $\mathbb{Z}/p$ with a prime number $p$ of elements as a field, the notation $\mathbb{F}_p=\mathbb{Z}/p$ is commonly used.

(There are actually finite fields $\mathbb{F}_q$ with $q$ elements for any prime power $q=p^r$ which we’ll see more of next term. However, one needs to be careful since $\mathbb{F}_q$ is not the same as $\mathbb{Z}/q$ unless $q$ itself is prime.)

$(d)$ The polynomial rings $\mathbb{Z}[x]$ and $\mathbb{R}[x]$ are integral domains. More generally, if $R$ is an integral domain, then so is $R[x]$. To see this, suppose we have two non-zero polynomials \[f(x)=a_mx^m+\cdots+a_1x+a_0 \quad\text{and}\quad g(x)=b_nx^n+\cdots+b_1x+b_0\] in $R[x]$ where $a_m$ and $b_n$ are non-zero. The coefficient of $x^{m+n}$ in $f(x)g(x)$ is $a_mb_n$ which is non-zero since $R$ is an integral domain. But that means $f(x)g(x)$ is non-zero, implying that $R[x]$ is an integral domain. However, $R[x]$ is not a field since it doesn’t contain $x^{-1}$.

$(e)$ If $R$ is an integral domain with non-zero $f(x), g(x)\in R[x]$, then looking at the leading coefficient as above shows that $\deg(f(x)g(x))=\deg f(x)+\deg g(x)$. This nice “multiplicative property” of degrees explains why we made the convention about the degree of the zero polynomial being $-\infty$. We want $\deg(0)=\deg(0\cdot g(x))=\deg(0)+\deg g(x)$ for any $n=\deg g(x)$.

However, notice this multiplicative property does not necessarily hold when $R$ is not an integral domain. For instance, if $R=\mathbb{Z}/6$, what is the degree of $(2x+1)(3x+1)$ in $R[x]$? All we can say generally is that $\deg(f(x)g(x))\leq(\deg f(x))(\deg g(x))$.

0.1.4 Homomorphisms of rings

Some maps between objects are nicer than others, in that they preserve some specific structure. Recall the definition of a ring homomorphism from Algebra II. Since we are working with a modified definition of rings which are commutative and have a multiplicative identity, it’s convenient to modify the definition of a ring homomorphism accordingly - we include an extra condition that ring homomorphisms preserve the multiplicative identity.

Definition 0.4 Let $R$ and $S$ be rings. A map $\varphi:R\to S$ is a called a ring homomorphism if it preserves the additive and multiplicative structures. In other words, for any $a, b\in R$, we have \[\varphi(a+_Rb)=\varphi(a)+_S\varphi(b),\qquad \varphi(a\cdot_Rb)=\varphi(a)\cdot_S\varphi(b)\] \[\text{and}\quad \varphi(1_R)=1_S.\] Furthermore, if $\varphi$ is also a bijection then it is called an isomorphism (and $R$ and $S$ are said to be isomorphic, which we write as $R\cong S$).

Example 0.3 $(a)$ There is always the zero homomorphism defined by $\varphi(r)=0_S$ for all $r\in R$.

$(b)$ There is always the identity homomorphism from a ring to itself, i.e. $\id_R:R\to R$ mapping $r\mapsto r$ for all $r\in R$. More generally, if $R$ is a subring of $S$ then the inclusion map $\iota_R:R\to S$ mapping $r\mapsto r$ is a ring homomorphism.

$(c)$ There are specialisation homomorphisms formed by substituting values into polynomials: given a ring $S$, a subring $R\subset S$ and any $a\in S$, the map \[\begin{align*} \varphi_a\;:\; R[x] &\longrightarrow \;\,S \\ f(x) &\longmapsto f(a) \end{align*}\] is a ring homomorphism from the polynomial ring $R[x]$ to $S$. A particular example of this (that we’ll return to later) is the ring homomorphism \[\begin{align*} \varphi\;:\; \mathbb{R}[x] &\longrightarrow \;\,\mathbb{C} \\ f(x) &\longmapsto f(i). \end{align*}\]

$(d)$ Here is a map that isn’t a ring homomorphism: multiplication of integers by $2$. Can you see why? \[\begin{align*} \varphi\;:\; \mathbb{Z} &\longrightarrow \mathbb{Z} \\ n &\longmapsto 2n. \end{align*}\]

Let’s record some direct properties from the definition, showing that ring homomorphisms work nicely with identities and inverses:

Lemma 0.1 Suppose $\varphi:R\to S$ is a ring homomorphism. Then

$\;\;(i)$ we have $\varphi(0_R)=0_S$ and $\varphi(-r)=-\varphi(r)$ for any $r\in R$.

$\;\;(ii)$ we have $\varphi(1_R)=1_S$ and $\varphi(r^{-1})=\varphi(r)^{-1}$ for any $r\in R^\times$. (Notice we need $r$ invertible here.)

Proof. $(i)$ Just notice that \[\varphi(0_R)+\varphi(0_R)=\varphi(0_R+0_R)=\varphi(0_R) \quad\implies\quad \varphi(0_R)=0_S.\]

Now using this, for any $r\in R$ we have \[\varphi(r)+\varphi(-r)=\varphi(r+(-r))=\varphi(0_R)=0_S.\] This property uniquely determines the additive inverse of $\varphi(r)$ so we must have $\varphi(-r)=-\varphi(r)$ as required.

$(ii)$ The condition $\varphi(1_R)=1_S$ is part of our definition of a ring homomorphism (but see the Exercises for an alternative way to deal with this - it follows from the other axioms when $\varphi$ is non-zero and $S$ is an integral domain).

Now using this, for any $r\in R^{\times}$ we have \[\varphi(r)\cdot\varphi(r^{-1})=\varphi(r\cdot r^{-1})=\varphi(1_R)=1_S.\] This property uniquely determines the multiplicative inverse of $\varphi(r)$ so we must have $\varphi(r^{-1})=\varphi(r)^{-1}$ as required.

0.1.5 Kernels and ideals

Given a ring homomorphism $\varphi:R\to S$, we can define its kernel and image \[\begin{align*} \ker(\varphi) &= \left\{r\in R \;|\; \varphi(r)=0_S\right\} \\ \text{and}\quad\im(\varphi) &= \left\{s\in S \;|\; s=\varphi(r)\text{ for some $r\in R$}\right\}. \end{align*}\] Just like with vector space homomorphisms, these two objects measure how far a ring homomorphism is from being an isomorphism:

Lemma 0.2 A ring homomorphism $\varphi:R\to S$ is

$\;(i)$ surjective if and only if $\im(\varphi)=S$,

$\;(ii)$ injective if an only if $\ker(\varphi)=\left\{0_R\right\}$.

The first part is essentially the definition of surjectivity (and surjective homomorphisms are sometimes called epimorphisms). The second part takes a short argument - see if you can prove it or look back at the Algebra II notes. (Injective homomorphisms are sometimes called embeddings or monomorphisms.)

It is straightforward to check that $\im(\varphi)$ is a subring of $S$, as long as $\varphi(1_R)=1_S$ - one just has to verify that it is closed with respect to the operations.

On the other hand, $\ker(\varphi)$ is not usually a subring of $R$ (at least not with our definitions - remember our rings all contain a multiplicative identity $1$). However, it is something close - it is an ideal. This is an additive subgroup of $R$ which “absorbs” elements of $R$, i.e. $I\cdot R\subset I$. Formally,

Definition 0.5 A subset $I\subset R$ of a ring $R$ is called an ideal in $R$ if:

$\;\;(i)$ $0_R\in I$, (this ensures that $I$ is non-empty)

$\;\;(ii)$ if $r, s\in I$ then $r\pm s\in I$,

$\;\;(iii)$ if $a\in I$ and $r\in R$ then $a\cdot r\in I$.

Example 0.4 Recall the following examples from Algebra II (along with the proofs…)

$(a)$ Every ring $R$ has the trivial ideals $\{0\}$ and $R$. In fact, $R$ is a field if and only if these are the only ideals in $R$.

$(b)$ The ideals in $\mathbb{Z}$ are precisely $a\mathbb{Z}=\left\{an \;|\; n\in\mathbb{Z}\right\}$ for each $a\in\mathbb{N}_0$.

$(c)$ More generally, a ring $R$ has the ideals $(a)=aR=\left\{ar \;|\; r\in R\right\}$ for each $a\in R$. These ideals generated by a single element are called principal ideals. An integral domain in which all ideals are principal (such as $\mathbb{Z}$ above) is called a principal ideal domain.

$(d)$ If $K$ is a field, then the non-trivial ideals in the polynomial ring $K[x]$ are all principal ideals, that is, $\left(f(x)\right)=\left\{f(x)g(x) \;|\; g(x)\in K[x]\right\}$ where $f(x)\in K[x]$ is any polynomial of degree at least $1$.

$(e)$ For any ring homomorphism $\varphi:R\to S$, the kernel $\ker(\varphi)$ is an ideal in $R$.

0.1.6 Quotient rings

Given a ring $R$ and an ideal $I\subset R$, we can define the quotient ring $R/I$. It is constructed as follows:

The elements of $R/I$ are cosets $r+I=\left\{r+i \;|\; i\in I\right\}$ where $r\in R$. These are “translates” of $I$ inside $R$ and two cosets $r+I$ and $s+I$ are equal precisely when $r-s\in I$.
One can verify that $R$ decomposes into a disjoint union of cosets. These include $0+I$ which will be the additive identity in $R/I$ and $1+I$ which will be the multiplicative identity in $R/I$.
The operations on $R/I$ are induced from those on $R$: given two cosets $r+I$ and $s+I$, we set \[(r+I)+(s+I)=(r+s)+I\quad\text{and}\quad (r+I)\cdot(s+I)=(rs)+I.\]

Verifying that this gives a well-defined ring structure takes some (quite tedious) effort but boils down to the fact that $I+I=I$ and $I\cdot R\subset I$.

Question: Does every ideal in a ring $R$ appear in the form $I=\ker(\varphi)$ for a suitable ring homomorphism $\varphi$ from $R$ to another ring? (In other words, we know kernels are always ideals, but are ideals always kernels?)

The quotient ring construction tells us the answer is yes - the canonical projection \[\begin{align*} \pi_I\;:\; R &\longrightarrow R/I \\ r &\longmapsto r+I. \end{align*}\] is a surjective ring homomorphism with kernel $\ker(\pi_I)=I$. This canonical projection satisfies a “universal property”: given any ring $S$ and homomorphism $\varphi:R\to S$ with $I\subset\ker(\varphi)$, there is another ring homomorphism $\overline{\varphi}:R/I\to S$ making the following diagram “commute”.

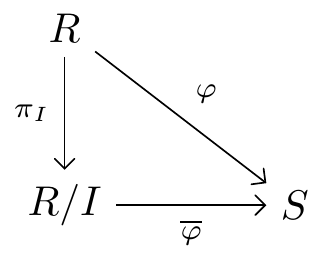
This means that following the two different paths from $R$ to $S$ gives the same thing, i.e. $\varphi=\overline{\varphi}\circ\pi_I$. In fact, the map $\overline{\varphi}$ is uniquely defined by $\overline{\varphi}(r+I)=\varphi(r)$. The First Isomorphism Theorem states that if $\varphi$ is surjective and $I$ equals $\ker(\varphi)$, then $\overline{\varphi}$ is an isomorphism. So $\pi_I:R\to R/I$ is essentially the only surjective homomorphism from $R$ with kernel $I$.

Theorem 0.1 (First Isomorphism Theorem for rings) Let $\varphi:R\to S$ be a surjective ring homomorphism. Then the map \[\begin{align*} R/\ker(\varphi) &\;\tilde{\longrightarrow} \; S \\ r+\ker(\varphi) &\longmapsto \varphi(r) \end{align*}\] is an isomorphism.

The above is quite abstract and involves a fair bit of checking to prove the details. It’s much easier to get the idea via examples:

Example 0.5 $\,$

$(a)$ Consider the reduction modulo $n$ map for integer $n\geq 2$: \[\begin{align*} \varphi_n\;:\; \mathbb{Z} &\longrightarrow \mathbb{Z}/n \\ a &\longmapsto a\bmod n \end{align*}\] This is a clearly a surjective ring homomorphism with kernel $\ker(\varphi_n)=n\mathbb{Z}$. As a result, the above theorem tells us $\mathbb{Z}/n\mathbb{Z}\cong \mathbb{Z}/n$ as one would hope! (Actually, $\mathbb{Z}/n\mathbb{Z}$ is a very common notation for the ring of integers modulo $n$.)

$(b)$ Consider the specialisation homomorphism \[\begin{align*} \varphi_2\;:\; \mathbb{R}[x] &\longrightarrow \;\mathbb{R} \\ f(x) &\longmapsto f(2) \end{align*}\] It’s clearly surjective since constant polynomials give every element in $\mathbb{R}$. The kernel consists of polynomials having $2$ as a root. In other words, $\ker(\varphi_2)=(x-2)$, i.e. the ideal of polynomials divisible by $x-2$. We obtain an isomorphism $\mathbb{R}[x]/(x-2)\cong\mathbb{R}$.

Similarly, we can show $R[x]/(x-a)\cong R$ for any polynomial ring $R[x]$ and $a\in R$.

$(c)$ Consider the specialisation homomorphism \[\begin{align*} \varphi_i\;:\; \mathbb{R}[x] &\longrightarrow \;\mathbb{C} \\ f(x) &\longmapsto f(i) \end{align*}\] Again, this is surjective since an arbitrary complex number $a+bi$ is the image of at least one polynomial, e.g. $a+bx\mapsto a+bi$. Furthermore, if $f(x)\in\ker(\varphi_i)$ then $i$ is a root of $f(x)$. But since $f(x)$ has real coefficients, the conjugate $-i$ is also a root and so $f(x)$ is divisible by $(x-i)(x+i)=x^2+1$. In particular, we find that $\ker(\varphi_i)=(x^2+1)$ and $\varphi_i$ induces a ring isomorphism \[\mathbb{R}[x]/(x^2+1)\cong\mathbb{C}.\]

$(d)$ Let’s determine the structure of the quotient ring $\mathbb{R}[x]/(x^2-3x+2)$ using the Theorem.

First of all, notice $x^2-3x+2=(x-1)(x-2)$ has roots $1$ and $2$. Now consider the map \[\begin{align*} \varphi\;:\; \mathbb{R}[x] &\longrightarrow \;\;\;\mathbb{R}\times\mathbb{R} \\ f(x) &\longmapsto \left(f(1),f(2)\right) \end{align*}\] The zero element in $\mathbb{R}\times\mathbb{R}$ is $(0,0)$ so any $f(x)\in\ker(\varphi)$ must have $f(1)=f(2)=0$. This happens precisely when $f(x)$ is divisible by $(x-1)(x-2)=x^2-3x+2$ and so $\ker(\varphi)=(x^2-3x+2)$.

On the other hand, $\varphi$ is surjective. To see this, let’s just write down a specific polynomial that maps to an arbitrary element $(a,b)\in\mathbb{R}\times\mathbb{R}$. We want $f(1)=a$ and $f(2)=b$ and there’s always a linear polynomial that interpolates two values. After a tiny bit of algebra we find \[f(x)=(b-a)x+(2a-b) \quad\implies\quad \varphi(f(x))=(a,b).\] In particular, we’ve discovered that \[\mathbb{R}[x]/(x^2-3x+2)\cong\mathbb{R}\times\mathbb{R}.\]

Compare this with the previous example: $\mathbb{R}[x]/(x^2+1)$ is a field whereas $\mathbb{R}[x]/(x^2-3x+2)$ is not. This different behaviour is due to $x^2+1$ being irreducible over $\mathbb{R}$, whereas $x^2-3x+2$ is not.

Note, example $(d)$ is essentially a special case of the Chinese Remainder Theorem for (commutative) rings that we saw in Algebra II: if $I$ and $J$ are ideals in a ring $R$ such that $I+J=R$, then we have ring isomorphism \[\begin{align*} R/(I\cap J) &\;\;\;\tilde{\longrightarrow} \;\;\; R/I \times R/J \\ r+(I\cap J) &\;\;\longmapsto \left(r+I,r+J\right) \end{align*}\] In our example, we have $R=\mathbb{R}[x]$, $I=(x-1)$, $J=(x-2)$ and so $I\cap J=\left(x^2-3x+2\right)$. From example $(b)$ above, we know that $R/I\cong R/J\cong\mathbb{R}$.

0.2 Group Theory

0.2.1 Definitions and basic facts

Definition 0.6 A group is a set $G$ with a binary operation $\circ$ which maps each (ordered) pair $g, h\in G$ to another element $g\circ h\in G$, where we demand the following properties.

$\quad\;\;$(associativity): $(a\circ b)\circ c=a\circ(b\circ c)$ for any $a, b, c\in G$,

$\quad\;\;$(identity): there exists an additive identity $e\in G$ such that $e\circ g=g\circ a=a$ for all $g\in G$,

$\quad\;\;$(inverses): every element $g\in G$ has an inverse $h\in G$ such that $g\circ h=h\circ g=e$.

One easily checks that in any group, there is only one identity $e$ and each element $g$ has only one inverse, which we write as $g^{-1}$.

Definition 0.7 A group $G$ is called abelian if the operation $\circ$ is commutative, i.e.

$\quad\;\;$(commutativity): $g\circ h=h\circ g$ for any $g, h\in G$.

Remark. Multiplicative notation is usually more convenient and we’ll just write $gh$ for $g\circ h$ in a general group. However, in the abelian case we more often use additive notation $g+h$ and write the identity as $0\in G$ and inverses as $-g$.

Definition 0.8 A subset $H$ of a group $G$ is called a subgroup if it is itself a group under the same group operation as $G$.

In Galois Theory, it will be very important to be able to list all the subgroups of a given finite group $G$. From the definition, a subset $H$ is a subgroup if

$\quad(i)$ $h_1, h_2\in H\implies h_1h_2\in H$, $\quad(ii)$ $e\in H$, $\quad(iii)$ $h\in H\implies h^{-1}\in H$.

When $H$ is finite, the first of these actually implies the other two:

Lemma 0.3 A non-empty finite subset $H$ of a group $G$ is a subgroup if and only if it is closed under the group operation in $G$, i.e. for any $h_1,h_2\in H$ we have $h_1h_2\in H$.

Proof. There is an identity $e$ in $G$ and any $h\in H$ is in $G$ so $h^{-1}$ does exist in $G$. We need to show that $e$ and $h^{-1}$ actually lie in the subset $H$.

Consider the elements $h, h^2, h^3,...$. By closure, they all belong to $H$. But since $H$ is finite, they can’t all be distinct and so $h^i=h^j$ for some $i, j\in\mathbb{N}$ with $i>j$.

Now $h^j$ has an inverse in $G$, namely$\left(h^j\right)^{-1}=h^{-j}\in G$. Hence we have $h^{i-j}=h^{i}h^{-j}=e$ in $G$. But $i-j\in\mathbb{N}$ so $h^{i-j}=e$ is in $H$ as required. Furthermore, we obtain $h^{-1}=h^{i-j-1}$ is in $H$ as well so we are done.

Notice how the finiteness of $H$ was crucial in this argument.

In the rest of this section, we will assume that all groups are finite and write $|G|$ for the order of $G$, i.e. the number of elements in $G$. The order of subgroups is very restricted:

Theorem 0.2 (Lagrange's Theorem) If $H$ is a subgroup of a finite group $G$, then $|H|$ divides $|G|$.

This is proved using the concept of left cosets of $H$ in $G$, i.e. the subsets \[gH=\left\{ gh \;|\; h\in H\right\}\quad\text{for $g\in G$.}\] Using the group axioms, one shows these all have $|H|$ elements and $G$ is a disjoint union of the distinct left cosets so $|H|$ divides $|G|$.

Similarly, one has right cosets $Hg=\left\{ hg \;|\; h\in H\right\}$ for $g\in G$ and the number of distinct right cosets equals the number of distinct left cosets. This number is called the index of $H$ in $G$ and is denoted by $(G:H)=|G|/|H|$.

For Galois Theory, not only do we need to know the subgroups of a given group $G$, it will also be important to know when they are normal.

Definition 0.9 A subgroup $H$ of a group $G$ is normal if $gH=Hg$ for any $g\in G$. Equivalently, the sets of left cosets and right cosets coincide.

Example 0.6 $\,$

$(a)$ If $(G:H)=1$, i.e. $H=G$ then $H$ is normal in $G$.

Indeed, there is only one (left or right) coset $H=G$ and $gH=Hg=G$ for all $g\in G$.

$(b)$ If $(G:H)=2$, the $H$ is a normal subgroup in $G$.

In this case, we can quite easily list all the cosets. Choose $g\in G\setminus H$ (that is $g\in G$ with $g\not\in H$). Then $gH=G\setminus H$ and $G$ is the disjoint union of the two distinct left cosets $H=eH$ and $gH$.

Furthermore, $He=H=eH$ but also, $Hg=G\setminus H=gH$. As a result, the left and right cosets coincide and $H$ is normal.

$(c)$ If $G$ is an abelian group, then every subgroup $H$ in $G$ is normal since clearly $gH=Hg$ always.

Due to this fact, normality is only a non-trivial issue for non-abelian groups.

$(d)$ Let’s write down a non-normal subgroup. We know we need a non-abelian group so take the smallest one $G=S_3$. This is the group of permutations of three elements $1, 2, 3$ and we’ll take $H$ to be a subgroup of order $2$. Using cycle notation, let’s define $H=\left\{e, (1\,2)\right\}$. Then (with right-to-left composition as in Algebra II),

$(1\,3)H=\left\{(1\,3), (1\,2\,3)\right\}$ whereas $H(1\,3)=\left\{(1\,3), (1\,3\,2)\right\}$

but the $3$-cycles $(1\,2\,3)$ and $(1\,3\,2)$ are not equal. (In fact, they’re inverses of each other.)

0.2.2 Homomorphisms and quotient groups

A group homomorphism is a map between groups that is compatible with the group structures (just like the ring homomorphisms earlier but easier!)

Definition 0.10 A group homomorphism between two groups $G$, $H$ with respective operations $\circ_G$ and $\circ_H$ is a map $\varphi:G\to H$ satisfying \[\varphi(g_1\circ_G g_2)=\varphi(g_1)\circ_H\varphi(g_2)\quad\text{for all $g_1, g_2\in G$.}\] Furthermore, if $\varphi$ is also a bijection then it is called an isomorphism (and $G$ and $H$ are said to be isomorphic, which we write as $G\cong H$).

This definition automatically implies that $\varphi(e_G)=e_H$ and $\varphi(g^{-1})=\varphi(g)^{-1}$ for any $g\in G$.

We define the kernel and image of a group homomorphism $\varphi:G\to H$ by \[\begin{align*} \ker(\varphi) &= \left\{g\in G \;|\; \varphi(g)=e_H\right\} \\ \text{and}\quad\im(\varphi) &= \left\{h\in H \;|\; h=\varphi(g)\text{ for some $g\in G$}\right\}. \end{align*}\] One easily checks that $\ker(\varphi)$ is a subgroup of $G$ and $im(\varphi)$ is a subgroup of $H$. However, the kernel is nicer in that it is always a normal subgroup of $G$.

This leads us to the concept of a quotient group, which is similar to the case of quotient rings where the role of ideals is played by normal subgroups. Given a group $G$ and a normal subgroup $N\in G$, the quotient group $G/N$ is constructed as follows:

The elements of $G/N$ are the cosets $gN$ where $g\in G$.
The composition on $G/N$ is induced from that of $G$: given cosets $g_1N$ and $g_2N$ we set \[(g_1N)(g_2N)=(g_1g_2)N.\]
The identity element is just $eN=N$ and inverses are given by $(gN)^{-1}=g^{-1}N$ for $g\in G$.

Note it is very important that $N$ is normal, otherwise the above construction doesn’t make sense.

Question: Does every normal subgroup in a group $G$ appear in the form $N=\ker(\varphi)$ for a suitable group homomorphism $\varphi$ from $G$ to another group? (In other words, we know kernels are always normal subgroups, but are normal subgroups always kernels?)

As in the ring case, the answer is positive. Given a normal subgroup $N$ in $G$, there is a group homomorphism (the canonical projection) \[\begin{align*} \pi_N\;:\; G &\longrightarrow G/N \\ g &\longmapsto gN. \end{align*}\] Moreover, this is surjective and has kernel $\ker(\pi_N)=N$. Finally, we also have the First Isomorphism Theorem linking the kernel and image of a group homomorphism.

Theorem 0.3 (First Isomorphism Theorem for groups) Let $\varphi:G\to G'$ be a group homomorphism. Then the map \[\begin{align*} G/\ker(\varphi) &\;\tilde{\longrightarrow} \; \im(\varphi) \\ g\ker(\varphi) &\longmapsto \varphi(g) \end{align*}\] is an isomorphism.

0.2.3 Direct products of groups

Given groups $G$ and $H$, the direct product $G\times H$ is the set of pairs $(g,h)$ with $g\in G$, $h\in H$ with group structure defined component-wise by \[(g_1,h_1)(g_2,h_2)=(g_1g_2,h_1h_2).\] Note that associativity follows from the associativity in $G$ and $H$, the identity element is $(e_G,e_H)$ and inverses are given by $(g,h)^{-1}=(g^{-1},h^{-1})$.

This is a very natural construction that allows us to create lots of new groups from ones we know. We’ll see some examples soon, but for now we’ll just record a couple of nice general properties.

A direct product $G\times H$ contains isomorphic copies of $G$ and $H$ as subgroups: \[\left\{(g,e_H) \;|\; g\in G\right\}\cong G \quad\text{and}\quad \left\{(e_G,h) \;|\; h\in H\right\}\cong H.\] Furthermore, elements from these two subgroups commute: \[ (g,e_H)(e_G,h)=(g,h)=(e_G,h)(g,e_H)\quad\text{for all $g\in G$, $h\in H$.}\]

One also has a “uniqueness property” for direct products of subgroups:

Suppose $G_1$ and $G_2$ are subgroups of a group $G$ with trivial intersection $G_1\cap G_2=\{e_G\}$.
Further, suppose that elements of $G_1$ and $G_2$ commute, i.e. $g_1g_2=g_2g_1$ for all $g_1\in G_1$, $g_2\in G_2$. Then $G$ has a unique minimal subgroup containing both $G_1$ and $G_2$ and this subgroup is isomorphic to $G_1\times G_2$.

As a consequence of the above, we have the following very useful fact for in studying subgroups of finite abelian groups:

If $|G|=mn$ where $\gcd(m,n)=1$, then there are unique subgroups $G_1$, $G_2$ of $G$ with \[|G_1|=m,\quad |G_2|=n\quad\text{and}\quad G\cong G_1\times G_2.\]

0.2.4 Typical examples of groups

We’ll end this recap of facts from Algebra II with a list of examples of finite groups you should be familiar with already, as well as some of their properties.

$(a)$ Cyclic groups.

If there is an element $g\in G$ such that $G=\left\{e, g, g^2,...,g^{n-1}\right\}$, then $G$ is a cyclic group of order $|G|=n$ and $g$ is a generator. We often use the notation $G=\langle\, g\,\rangle$ for the cyclic group with generator $g$.

Note that cyclic groups are always abelian.
We also have $g^n=e$ and a power $g^k$ is another generator precisely when $\gcd(k,n)=1$.
Any subgroup of $G$ is also cyclic and has order $d$ for some $d$ dividing $n$. Conversely, for any $d$ dividing $n$, there is a unique subgroup of order $d$ in $G$ and this subgroup is generated by $g^{n/d}$.
Since $G$ is abelian, all of its subgroups are normal.
A cyclic group of order $n$ is isomorphic $\mathbb{Z}/n$, i.e. the integers modulo $n$ with addition. An explicit isomorphism is given by the map \[\begin{align*} \mathbb{Z}/n\;\;\; &\longrightarrow G \\ m\bmod n &\longmapsto g^m \end{align*}\]
If the order of a group $G$ is prime $|G|=p$, then $G$ is cyclic (and so is isomorphic to $\mathbb{Z}/p$).

$(b)$ Direct products of cyclic groups.

The fundamental property here is that

Lemma 0.4 If $gcd(m,n)=1$, then $\mathbb{Z}/(mn)\cong\mathbb{Z}/n\,\times\,\mathbb{Z}/m$.

Proof. This is a consequence of the Chinese Remainder Theorem for rings, where we “forget” about the multiplicative structure in the rings.

Alternatively, we can prove it using the general properties of direct products given earlier. Since $G=\mathbb{Z}/(mn)$ is cyclic and $m$, $n$ clearly divide $mn$, we know there are unique subgroups \[G_1\cong\mathbb{Z}/m\quad\text{and}\quad G_2\cong\mathbb{Z}/n\quad\text{in $G$.}\] Now, the order of $G_1\cap G_2$ must divide $m$ and $n$, but since $\gcd(m,n)=1$, that means $G_1\cap G_2$ is trivial. Furthermore, elements from these two subgroups commute with one another (since they live in the abelian group $G$).

Hence using the property stated earlier about direct products, $G_1\times G_2$ is (isomorphic to) a subgroup of $G$. Finally, by considering the orders $|G_1\times G_2|=mn=|G|$, we see $G\cong G_1\times G_2$ as required.

For instance, $\mathbb{Z}/15\cong\mathbb{Z}/3\,\times\,\mathbb{Z}/5$. We do need to take care with the $\gcd$ property, though. For instance, $\mathbb{Z}/18\not\cong\mathbb{Z}/3\,\times\,\mathbb{Z}/6$. (Can you see why? Think about orders of elements…)

We can extend this to products of more than two cyclic groups, e.g. $\mathbb{Z}/30\cong\mathbb{Z}/2\,\times\,\mathbb{Z}/3\,\times\,\mathbb{Z}/5$ and more generally, we can classify all finite abelian groups in the following way:

Theorem 0.4 Any finite abelian group $G$ is a product of cyclic groups, i.e. there are $d_1,...,d_k\in\mathbb{N}$ such that $G$ is isomorphic to a group of the form \[\mathbb{Z}/d_1\,\times\,...\,\times\,\mathbb{Z}/d_k.\] Furthermore, if we demand that $d_1>1$ and $d_1\,|\,d_2\,|\,...\,|\,d_k$, then this form is unique.

For instance, (up to isomorphism) there are

two different abelian groups $\mathbb{Z}/4$ and $\mathbb{Z}/2\times\mathbb{Z}/2$ of order $4$,
three different abelian groups $\mathbb{Z}/8$, $\mathbb{Z}/2\times\mathbb{Z}/4$ and $\mathbb{Z}/2\times\mathbb{Z}/2\times\mathbb{Z}/2$ of order $8$.

$(c)$ Dihedral groups

For $n\geq 3$, the dihedral group $D_n$ (of order $2n$) is the group of symmetries (i.e. reflections and rotations) of the regular $n$-gon.

It is generated by two elements $r$ and $s$ with three relations $r^n=e$, $s^2=e$ and $rs=sr^{-1}$ (and since $n\geq 3$, it is non-abelian). We sometimes use the generator-relation notation \[D_n=\langle\, r,s\,\mid r^n=e, s^2=e, rs=sr^{-1}\,\rangle\] or more succinctly, $\langle\, r,s \,\rangle$ where the relations are implicitly understood.
We can list the elements $D_n=\left\{e, r,..., r^{n-1}, s, sr,..., sr^{n-1}\right\}$.
Clearly $D_n$ contains the cyclic subgroup $\langle\,r\,\rangle=\left\{e, r,..., r^{n-1}\right\}\cong\mathbb{Z}/n$ of order $n$. This is a normal subgroup since it has index $2$ in $D_n$. Also notice that this subgroup is the kernel of of the surjective homomorphism $D_n\to\mathbb{Z}/2$ that maps $s^ir^j\mapsto j\mod 2$.
The elements $s, sr, ...,sr^{n-1}$ all have order $2$ so $D_n$ contains $n$ different cyclic subgroups of order $2$ given by $H_i=\left\{e,sr^i\right\}\cong\mathbb{Z}/2$ for each $0\leq i\leq n-1$. However, these are not normal subgroups. Indeed, notice \[rH_i=H_ir\quad\implies\quad rsr^{i}=sr^{i+1}\quad\implies\quad rs=sr.\] But also $rs=sr^{-1}$ so this implies $r^2=1$ which is false for $n\geq 3$.

$(d)$ Symmetric and alternating groups

For $n\in\mathbb{N}$, the symmetric group $S_n$ is the group of all permutations of $n$ symbols $\{1,...,n\}$.

When $n>1$, the alternating group $A_n$ is the subgroup of even permutations in $S_n$.

We have $|S_n|=n!$ and $S_n$ is generated by $2$-cycles. It is non-abelian when $n\geq 3$.
We have $|A_n|=n!/2$ (note $n>1$) and $A_n$ is generated by $3$-cycles. It is non-abelian when $n\geq 4$.
The subgroup structure of $S_n$ is generally very complicated. In fact, any group of order $n$ is isomorphic to some subgroup of order $n$. (This is Cayley’s Theorem.)
On the other hand, $S_n$ doesn’t have very many normal subgroups. Note that $A_n$ is always a normal subgroup of $S_n$ since it has index $(S_n:A_n)=2$. However, one can show that $A_n$ is the only normal subgroup of $S_n$ when $n\geq 5$.

For (very) small $n$, we can identify these groups in terms of others:

$S_1=\{e\}$, $S_2\cong\mathbb{Z}/2$ and $S_3\cong D_3$.
$A_2=\{e\}$ and $A_3\cong\mathbb{Z}/3$.

The group $S_4$ has order $|S_4|=4!=24$ so is already quite big and complicated. As noted above, it contains the normal subgroup $A_4$ of order $12$. We can “realise” $S_4$ as the group of symmetries of a regular tetrahedron (rotations and reflections) and in that case, $A_4$ appears as the subgroup of rotations.

However, $S_4$ also contains one other normal subgroup which has order $4$ (isomorphic to the Klein $4$-group): \[N=\left\{ e, (1\,2)(3\,4), (1\,3)(2\,4), (1\,4)(2\,3)\right\}\cong\mathbb{Z}/2\times\mathbb{Z}/2.\] To check that $gN=Ng$ for all $g\in S_4$, remember that $S_4$ is generated by $2$-cycles. Alternatively, write down a surjective homomorphism $\varphi:S_4\to S_3$ with $N=\ker(\varphi)$ so $N$ is automatically normal.