3 Field extensions

3.1 Definition and examples

A field extension $L/K$ (read as “$L$ over $K$”) is a field $L$ containing another field $K$ as a subfield. Warning: despite the notation, $L/K$ is not a quotient and alternative notations are $L:K$ or more simply $K\subset L$. Field extensions are the central objects in Galois Theory in a similar way to how vector spaces are the central objects in Linear Algebra.

Remark. Strictly speaking, we should say exactly how the field $K$ sits inside $L$. This can be done by also including a homomorphism $\iota:K\to L$ in the definition which, by Lemma 2.2, is automatically an injection. Across mathematics, we often blur the distinction between injections and subsets. Given a set $B$ and a subset $A\subset B$, there’s the inclusion map $\iota:A\to B$ which is injective. On the other hand, an injective map $\varphi:A\to B$ between sets $A$, $B$ gives a subset $\im(\varphi)\subset B$ which is an (isomorphic) copy of $A$ inside $B$.

Example 3.1 $(a)\;$ The field $\mathbb{C}$ containing $\mathbb{R}$ in the natural way is a field extension $\mathbb{C}/\mathbb{R}$. Similarly, we have field extensions $\mathbb{C}/\mathbb{Q}$ and $\mathbb{R}/\mathbb{Q}$.

$(b)\;$ As in section 2.1, any field $L$ contains a unique prime subfield $K$, which is either $\mathbb{Q}$ or $\mathbb{F}_p$ for prime $p$. This is an extension $L/K$.

$(c)\;$ Let $L=\mathbb{Q}(\sqrt{2})=\{a+b\sqrt{2} \;|\; a,b\in\mathbb{Q}\}$. This contains $K=\mathbb{Q}$ (as the set of elements with $b=0$) and we have a field extension $\mathbb{Q}(\sqrt{2})/\mathbb{Q}$.

More generally, we saw in Section 1.4 of the Introduction that if $\theta\in\mathbb{C}$ is a root of an irreducible quadratic polynomial $f(x)=x^2+px+q\in\mathbb{Q}[x]$, then \[\mathbb{Q}(\theta)=\{a+b\theta \;|\; a,b\in\mathbb{Q}\}\] is a field extension over $\mathbb{Q}$.

$(d)\;$ Let $L=\mathbb{Q}(\sqrt[3]{2})$ be the minimal subfield of $\mathbb{R}$ containing $K=\mathbb{Q}$ and $\sqrt[3]{2}$, the real cube root of $2$. Then $\mathbb{Q}(\sqrt[3]{2})/\mathbb{Q}$ is a field extension and later on we’ll see its elements can be written uniquely in terms of $3$ parameters \[\mathbb{Q}(\sqrt[3]{2})=\{a+b\sqrt[3]{2}+c\sqrt[3]{4} \;|\; a,b,c\in\mathbb{Q}\}.\]

$(e)\;$ Given a field $K$, consider the field $L=K(t)$ of rational expressions (ratios of polynomials with indeterminate $t$ and coefficients in $K$). This contains a copy of $K$ as the constant rational expressions $a/1$ for $a\in K$, so we have a field extension $K(t)/K$.

Examples $(c)$, $(d)$ and $(e)$ above involve “adjoining” a single element to the base field $K$ to construct $L$. These are called simple field extensions. We can generalise the idea with consistent notation in the following definition.

Definition 3.1 Let $L/K$ be a field extension and $S$ be a subset of $L$. We write $K(S)$ for the minimal subfield of $L$ that contains both $K$ and $S$, and call it “$K$ with $S$ adjoined”.

As an example, we can consider adjoining $S=\{\sqrt{2},\sqrt{7}\}$ to $\mathbb{Q}$ to obtain an extension $\mathbb{Q}(\sqrt{2},\sqrt{7})/\mathbb{Q}$. Later on, we’ll see that elements of this can be written uniquely in terms of $4$ parameters: \[\mathbb{Q}(\sqrt{2},\sqrt{7})=\left\{ a+b\sqrt{2}+c\sqrt{7}+d\sqrt{14} \;|\; a,b,c,d\in\mathbb{Q} \right\}.\] In Galois Theory, we will be very interested in “towers” of field extensions \[K\subset M\subset L\] where we fix the top and bottom fields $L$ and $K$ and let the middle field $M$ vary in between. For instance, in the extension $\mathbb{Q}(\sqrt{2},\sqrt{7})/\mathbb{Q}$ above, we have intermediate fields $\mathbb{Q}(\sqrt{2})$, $\mathbb{Q}(\sqrt{7})$ and $\mathbb{Q}(\sqrt{14})$. We can display this in a diagram as follows, where the lines denote inclusions and “bigger” fields appear higher up:

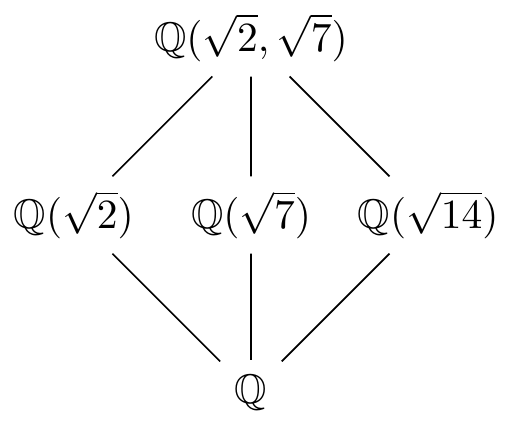
Interestingly, $\mathbb{Q}(\sqrt{2},\sqrt{7})/\mathbb{Q}$ is actually a simple extension - it can be written in the form $\mathbb{Q}(\alpha)$ for some $\alpha\in\mathbb{C}$. Can you find such an $\alpha$? On the other hand, the extension $\mathbb{C}/\mathbb{Q}$ is not simple - there is no $\alpha\in\mathbb{C}$ such that $\mathbb{C}=\mathbb{Q}(\alpha)$. Can you prove this?

Remark. For a field extension $L/K$, we’ll generally use Roman letters $a,b,...$ for elements of the smaller field $K$ and Greek letters $\alpha,\beta,...$ for elements of the big field $L$ not in $K$.

3.2 Algebraic elements and minimal polynomials

Our focus in Galois Theory is on roots of polynomial equations so it’s a good idea to have some general terminology for them:

Definition 3.2 Let $L/K$ be a field extension and $\theta\in L$. Then $\theta$ is algebraic over $K$ if there exists a non-zero polynomial $f(x)\in K[x]$ such that $f(\theta)=0$, and transcendental over $K$ otherwise.

Example 3.2 $(a)\;$ Let $n\geq 1$ and set $\theta=e^{2\pi i/n}\in\mathbb{C}$. Then $\theta$ is a root of $f(x)=x^n-1$ and so $\theta$ is algebraic over $\mathbb{Q}$.

$(b)\;$ The numbers $\pi$ and $e$ are famously transcendental over $\mathbb{Q}$. Showing that specific numbers are transcendental can be quite hard, but if you’re interested, there are proofs for $e$ and $\pi$ in Stewart’s book. Also, you’ve probably seen Cantor’s diagonal argument which shows in a precise sense that almost all real numbers are transcendental over $\mathbb{Q}$.

$(c)\;$ On the other hand, $\pi$ and $e$ are algebraic over $\mathbb{R}$ since they are both real numbers! For instance, $\pi$ is a root of $f(x)=x-\pi\in\mathbb{R}[x]$ and more generally, any $a\in K$ is algebraic over $K$. This shows it’s important to specify the field $K$ where the coefficients of our polynomials are allowed to live.

$(d)\;$ In the field $K(t)$ of rational expressions over a field $K$, the element $t\in K(t)$ is transcendental over $K$. In fact, we can prove rather more: given $\theta\in K(t)$ with $\theta\not\in K$, then $\theta$ is transcendental over $K$.

Proof. Suppose on the contrary that $\theta$ is algebraic over $K$ and so satisfies a polynomial equation \[f(\theta)=a_n\theta^n+a_{n-1}\theta^{n-1}+\cdots+a_1\theta+a_0=0\] with $a_i\in K$ and $a_0,a_n\neq 0$. Let $\theta=r/s$ where $r=r(t), s=s(t)\neq 0$ are in $K[t]$. By cancelling, we can assume they have no common factors (as polynomials in $t$). Substituting and multiplying by $s^n$ gives \[\begin{equation} 0=s^nf(\theta)=a_nr^n+a_{n-1}r^{n-1}s+\cdots+a_1rs^{n-1}+a_0s^n \tag{3.1} \end{equation}\] \[\implies r^n=-\frac{s}{a_n}\left(a_{n-1}r^{n-1}+\cdots+a_1rs^{n-2}+a_0s^{n-1} \right)\] which implies $r^n$ is divisible by $s$ in $K[t]$. Now $K[t]$ is a unique factorisation domain so actually $r$ is divisible by $s$. But since $r$, $s$ have no common factors, this means $s=s(t)$ must be a constant polynomial $s=s_0\in K$. Furthermore, (3.1) now shows the constant $a_0s_0^n$ is divisible by $r$ so $r=r(t)$ is constant $r=r_0\in K$ as well. Hence $\theta=r_0/s_0\in K$ gives the required contradiction.

As well as asking if an element is a root of a non-zero polynomial, it’s natural to consider the set of all polynomials which have the element as a root. Given a field extension $L/K$ and an element $\theta\in L$, define the following subset of $K[x]$ \[I_K(\theta)=\left\{f(x)\in K[x] \;|\; f(\theta)=0 \right\}.\] In other words, $I_K(\theta)$ is the set of polynomials which have $\theta$ as a root.

Lemma 3.1 The set $I_K(\theta)$ is an ideal in $K[x]$. Moreover,

$\;\;\,(i)$ if $\theta$ is transcendental over $K$, then $I_K(\theta)=\{0\}$,

$\;(ii)$ if $\theta$ is algebraic over $K$, then there is a unique irreducible monic polynomial $m(x)\in K[x]$ which generates $I_K(\theta)$. In particular, every polynomial in $f(x)\in K[x]$ with $f(\theta)=0$ is divisible by $m(x)$.

Proof. We can easily check directly that $I_K(\theta)$ fits the Definition 0.5 of an ideal.

It clearly contains the zero polynomial.
Given $f_1(x), f_2(x)\in I_K(\theta)$, then $f_1(\theta)=f_2(\theta)=0$ so $(f_1\pm f_2)(\theta)=0$. This means that $(f_1\pm f_2)(x)\in I_K(\theta)$.
Given $f(x)\in I_K(\theta)$ and $g(x)\in K[x]$, then $f(\theta)=0$ so $(fg)(\theta)=f(\theta)g(\theta)=0$. This means that $(fg)(x)\in I_K(\theta)$.

$(i)$ If $\theta$ is transcendental over $K$, then by definition, it isn’t a root of a non-zero polynomial so $I_K(\theta)=\{0\}$.

$(ii)$ If $\theta$ is algebraic over $K$, then by definition $I_K(\theta)\neq \{0\}$. Recall the important fact that $K[x]$ is a principal ideal domain. That means the ideal $I_K(\theta)$ can be generated by a single non-zero polynomial $m(x)\in K[x]$ and since it has a root $\theta$, we must have $\deg m(x)\geq 1$.

Furthermore, $m(x)$ must have minimal degree amongst all polynomials in $I_K(\theta)$, otherwise it couldn’t generate them all. This implies that $m(x)$ must be irreducible since, if $m(x)=g(x)h(x)$ with $\deg g(x),\deg h(x)\geq 1$, then $\theta$ is a root of one of the factors contradicting the minimality of the degree $\deg m(x)$.

Finally, multiplying the generator by a non-zero constant $c\in K^\times$ doesn’t change the ideal: $\left(m(x)\right)=\left(cm(x)\right)$ and so we can assume that $m(x)$ is monic. This uniquely determines the generator $m(x)$ and every polynomial $f(x)\in K[x]$ with $f(\theta)=0$ is divisible by $m(x)$.

This leads us to the important definitions of degrees and minimal polynomials of elements:

Definition 3.3 Let $L/K$ be a field extension and suppose that $\theta\in L$ is algebraic over $K$. The minimal polynomial of $\theta$ over $K$ is the unique monic polynomial $m(x)\in K[x]$ with $I_K(\theta)=(m(x))$. In this case, we say the degree of $\theta$ over $K$ is the degree of its minimal polynomial $\deg m(x)$.

Note transcendental elements don’t have minimal polynomials by definition.

A really useful consequence of the above lemma is that if a monic polynomial $f(x)\in K[x]$ satisfying $f(\theta)=0$ is irreducible over $K$, then $f(x)$ is automatically the minimal polynomial of $\theta$. Indeed, suppose $m(x)$ is the minimal polynomial, then the lemma tells us $m(x)|f(x)$. But if $f(x)$ is itself irreducible then it must then be a constant multiple of $m(x)$ and since they are both monic, we have $f(x)=m(x)$.

Example 3.3 $(a)$ Any $\theta\in K$ has minimal polynomial $m(x)=x-\theta\in K[x]$. In particular, all elements of $K$ are algebraic of degree $1$ over $K$.

$(b)$ The element $i=\sqrt{-1}\in\mathbb{C}$ has minimal polynomial $m(x)=x^2+1$ over $\mathbb{R}$ and has degree $2$. (There are clearly no linear polynomials with real coefficients with $i$ as a root.) Similarly $\sqrt{2}$ has minimal polynomial $x^2-2$ over $\mathbb{Q}$ and has degree $2$.

$(c)$ The minimal polynomial of $\theta=\sqrt[3]{2}$ over $\mathbb{Q}$ is $m(x)=x^3-2$ and $\theta$ has degree $3$. We know this because $x^3-2$ vanishes at $\theta$ and is irreducible over $\mathbb{Q}$ (e.g. by seeing it has no linear factors). Without knowing the above theory, this would be quite awkward. Try showing directly that $\theta$ doesn’t satisfy a quadratic polynomial over $\mathbb{Q}$, i.e. there are no $a,b\in\mathbb{Q}$ such that $\sqrt[3]{4}=a+b\sqrt[3]{2}$ - unless you’re careful, it easily turns into a mess!

3.3 Constructing simple field extensions

Our goal in Galois Theory is to study the solutions of polynomial equations so it’s important to find where these might live. Given a field $K$ and a polynomial $f(x)\in K[x]$, how can we find a field extension $L/K$ containing some root $\theta$ of $f(x)$?

When $K\subset\mathbb{C}$, we know the Fundamental Theorem of Algebra ensures that all roots of $f(x)$ are in $\mathbb{C}$ and so we could simply take $L=\mathbb{C}$. However, this is a really big extension - it contains lots of transcendental elements that are of no use in our goal. So perhaps we can avoid introducing these unnecessary elements by just adjoining the element $\theta\in\mathbb{C}$ to give the simple extension $K(\theta)/K$. Recall this is the minimal subfield of $\mathbb{C}$ containing $K$ and the particular root $\theta$.

But we now have a problem: what if $K$ is not a subfield of $\mathbb{C}$, for instance $K=\mathbb{F}_p$ or $K=\mathbb{Q}(t)$? Then we don’t have a ready-made big field like $\mathbb{C}$ which automatically contains all the roots we want. Our job is thus to build an extension over arbitrary $K$ from scratch purely using the polynomial $f(x)$. Actually, since a root $\theta$ of $f(x)$ is automatically a root of the minimal polynomial of $\theta$ over $K$, we lose nothing by only considering the minimal polynomial $m(x)\in K[x]$ of $\theta$, i.e. a monic and irreducible polynomial.

The key observation is that we can construct the required big fields abstractly via quotients of polynomial rings.

Lemma 3.2 Let $K$ be a field and $f(x)\in K[x]$ be a non-zero polynomial. Then \[\text{$f(x)$ is irreducible over $K$}\quad\iff\quad\text{$K[x]/\left(f(x)\right)$ is a field.}\]

Remark. This result is actually a special case of a theorem from Algebra II Michaelmas term: given a ring $R$ and ideal $I\subset R$, then $I$ is a maximal ideal in $R$ if and only if the quotient ring $R/I$ is a field. Here, $I=(f(x))$ being a maximal ideal in $K[x]$ corresponds exactly to $f(x)$ being irreducible.

Proof. Suppose $f(x)$ is irreducible over $K$ and consider the canonical projection \[\pi: K[x]\longrightarrow K[x]/\left(f(x)\right).\] We want to show that $L=K[x]/\left(f(x)\right)$ is a field. Firstly, $f(x)$ has degree at least $1$ so there is no $g(x)\in K[x]$ such that $f(x)g(x)=1$. In particular, the unit polynomial $1\not\in \left(f(x)\right)$ and \[1_L=\pi(1_K)\neq 0_L.\]

Secondly, we need to show every non-zero element in $L$ has a multiplicative inverse or equivalently, if $g(x)\in K[x]$ is not a multiple of $f(x)$, then $\pi\left(g(x)\right)$ is invertible in $L$. Now $f(x)$ is irreducible, so any factor of $f(x)$ is either $f(x)$ or $1$. But $f(x)\nmid g(x)$ so the greatest common divisor $\gcd\left(f(x),g(x)\right)=1$. By the Euclidean algorithm for polynomials, there are thus $a(x), b(x)\in K[x]$ such that \[a(x)f(x)+b(x)g(x)=1.\] Applying the ring homomorphism $\pi$ to both sides of this and using $\pi\left(f(x)\right)=0$ gives \[\pi\left(a(x)\right)\pi\left(f(x)\right)+\pi\left(b(x)\right)\pi\left(g(x)\right)=\pi(1)\quad\implies\quad \pi\left(b(x)\right)\pi\left(g(x)\right)=1\] and we’ve found $\pi\left(g(x)\right)$ is indeed invertible.

In the other direction, suppose that $L=K[x]/\left(f(x)\right)$ is a field. Then $\pi(1_K)=1_L\neq 0_L$ so $1_K\not\in\ker(\pi)=\left(f(x)\right)$. In particular, $f(x)$ is not a constant polynomial.

Suppose $f(x)=g(x)h(x)$ for some $g(x), h(x)\in K[x]$. Then \[\pi\left(g(x)\right)\pi\left(h(x)\right)=\pi\left(f(x)\right)=0\] and since $L$ is an integral domain, either $\pi\left(g(x)\right)=0$ or $\pi\left(h(x)\right)=0$. Without loss of generality, assuming $\pi\left(g(x)\right)=0$ we have $f(x)|g(x)$ so $g(x)=f(x)h'(x)$ for some $h'(x)\in K[x]$. Thus, using the fact that $f(x)$ is non-zero, \[f(x)=g(x)h(x)=f(x)h(x)h'(x)\quad\implies\quad h'(x)h(x)=1\] and so $h(x)\in K[x]$ must be a constant polynomial. Hence $f(x)$ is irreducible as required.

With this in hand, we obtain the construction we are looking for.

Theorem 3.1 Let $m(x)\in K[x]$ be a monic irreducible polynomial.

$\;\;(i)$ Then $K_m=K[x]/\left(m(x)\right)$ is a field extension over $K$.

$\;(ii)$ Let $\theta$ denote the image of $x$ under the canonical projection $\pi:K[x]\to K_m$. Then $\theta$ has minimal polynomial $m(x)$ and $K_m=K(\theta)$.

Proof. $(i)$ We’ve just shown that $K_m$ is a field in the previous lemma. Furthermore, there is the natural inclusion map $K\to K[x]$ sending $a\in K$ to the constant polynomial $a\in K[x]$. Composing this with the canonical projection $\pi:K[x]\to K_m=K[x]/\left(m(x)\right)$ gives a ring homomorphism \[K\longrightarrow K[x]\overset{\pi}\longrightarrow K_m.\] This is a homomorphism between fields so is injective and we agree to identify $K$ with its image in $K_m$, giving a field extension $K_m/K$.

$(ii)$ Explicitly, the canonical projection $\pi:K[x]\to K_m=K[x]/\left(m(x)\right)$ maps polynomials in $x$ to polynomials in $\theta$: \[\pi\left(\sum_i a_ix^i\right)=\sum_ia_i\theta^i.\] This is surjective with kernel equal to the set of polynomials that vanish at $\theta$. But $\ker(\pi)=\left(m(x)\right)$ so by the definition of minimal polynomials, $m(x)$ must be the minimal polynomial of $\theta$.

Any subfield of $K_m$ containing $K$ and $\theta$ contains every polynomial in $\theta$ with coefficients in $K$ as it is closed under addition and multiplication. But $K_m$ consists of exactly these, so is the minimal such subfield, and by definition that means $K_m=K(\theta)$ .

Using this, given a monic irreducible polynomial $m(x)\in K[x]$, we can always build a field extension of $K_m/K$ containing a root of $m(x)$. Now, there are many such extensions, for instance $m(x)=x^2-2$ has a root in $\mathbb{Q}(\sqrt{2})/\mathbb{Q}$ but also in $\mathbb{R}/\mathbb{Q}$ and in $\mathbb{C}/\mathbb{Q}$. But in some sense, $K_m$ is the canonical and minimal choice, as it satisfies a certain “universal property”. To make this precise, we introduce the following terminology.

Definition 3.4 Let $L_1$ and $L_2$ be extensions of a given field $K$ and $\varphi:L_1\to L_2$ be a field homomorphism. Then $\varphi$ is called a $K$-homomorphism if $\varphi(a)=a$ for all $a\in K$, i.e. $\varphi$ fixes elements of $K$. If furthermore $\varphi$ is an isomorphism of fields then it is called a $K$-isomorphism.

Example 3.4 Complex conjugation $z\mapsto\overline{z}$ is an $\mathbb{R}$-isomorphism $\mathbb{C}\to\mathbb{C}$. It’s a field isomorphism (it respects the field operations in $\mathbb{C}$) and $\overline{a}=a$ for all $a\in\mathbb{R}$. In a similar way, let $K$ be a field with characterstic not 2 and not containing a square root of $2$. Then \[m(x)=x^2-2\in K[x]\] is irreducible over $K$ and we can adjoin a root $\sqrt{2}$ to give an extension $K(\sqrt{2})/K$. We have a $K$-isomorphism \[\begin{align*} \sigma\;:\; K(\sqrt{2}) &\longrightarrow \,K(\sqrt{2}) \\ a+b\sqrt{2} &\longmapsto a-b\sqrt{2} \qquad\text{for $a,b\in K$}. \end{align*}\] These examples are actually $K$-isomorphisms between a field and itself - we call these $K$-automorphisms.

Here is the promised universal property of the extension $K_m/K$. As above, write $\theta$ for the image of $x$ under the canonical projection $\pi:K[x]\to K_m=K[x]/(m(x))$. Now suppose $L/K$ is some field extension with an element $\theta'\in L$ satisfying $m(\theta')=0$. Let $K_L(\theta')$ denote the minimal subfield in $L$ containing $K$ and $\theta'$. Note this field $K_L(\theta)$ depends on the choice of the bigger field, as well as on the choice of the root $\theta'\in L$. Indeed, it may be that $m(x)$ has several roots in $L$. The point is these choices don’t really matter and $K_L(\theta)$ is isomorphic to the field $K_m$ which is defined abstractly using just $K$ and $m(x)$. More precisely,

Proposition 3.1 There is a unique $K$-isomorphism $\varphi:K_m\rightarrow K_L(\theta')$ such that $\varphi(\theta)=\theta'$.

Proof. Recall the specialisation homomorphism $\psi:K[x]\to L$ which maps $f(x)\mapsto f(\theta')$. This is a ring homomorphism and its kernel \[\ker(\psi)=\{f(x)\in K[x] \;|\; f(\theta')=0\}.\] contains the irreducible polynomial $m(x)$, so $\ker(\psi)=(m(x))$.

We also have the canonical projection $\pi:K[x]\to K_m=K[x]/(m(x))$ and there is a homomorphism $\overline{\psi}:K_m\to L$ making the following diagram commute.

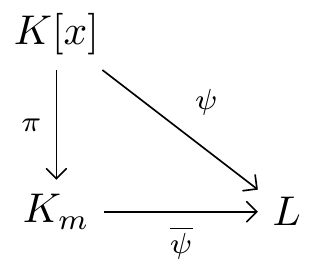
Explicitly,

for $a\in K$, we have $\overline{\psi}(a)=\overline{\psi}(\pi(a))=\psi(a)=a$, i.e. $\overline{\psi}$ is a $K$-homomorphism
and $\overline{\psi}(\theta)=\overline{\psi}(\pi(x))=\psi(x)=\theta'$.

Since $\overline{\psi}$ is a homomorphism between fields, it is automatically injective and its image is a subfield of $L$. This image is the minimal subfield of $K$ containing $K$ and $\theta'$ so equals $K_L(\theta')$. The First Isomorphism Theorem for rings gives the required $K$-isomorphism $\varphi:K_m\to K_L(\theta')$.

To prove uniqueness, recall that $K_m=K(\theta)$. One checks that given $K$-homomorphisms $\varphi_1,\varphi_2:K(\theta)\to M$ for a field extension $M/K$, if $\varphi_1(\theta)=\varphi_2(\theta)$, then $\varphi_1=\varphi_2$. We leave the details to the cautious reader.

In the above, we have described simple extensions $K(\theta)/K$ where $\theta$ is algebraic over $K$, i.e. where $\theta$ is a root of a polynomial $m(\theta)\in K[x]$. We can also consider a simple extensions $K(\theta)/K$ where $\theta$ is transcendental over $K$, i.e. where $\theta$ is not the root of any polynomial in $K[x]$. This is somewhat easier to describe and we have

Proposition 3.2 Let $\theta$ be transcendental over $K$ and consider the field $K(t)$ of rational expressions with indeterminate $t$. Then there is a unique $K$-isomorphism $\varphi:K(t)\to K(\theta)$ such that $\varphi(t)=\theta$.

We’ll just sketch the idea of the proof. One checks that the properties $\varphi(t)=\theta$ and $\varphi(a)=a$ for $a\in K$ lead to a field isomorphism \[\begin{align*} \varphi\;:\; K(t) &\longrightarrow \,K(\theta) \\ \frac{f(t)}{g(t)} &\longmapsto \frac{f(\theta)}{g(\theta)} \qquad\text{for $f(t),g(t)\in K[t]$ with $g(t)\neq 0$} \end{align*}\] and this is the unique field isomorphism with the required properties.

3.4 Explicit examples of simple extensions

Quadratic extensions

First, let’s consider some quadratic extensions, i.e. field extensions $K(\theta)/K$ where $\theta$ is a root of an irreducible quadratic polynomial. A typical situation is as follows:

Suppose $r\in K^\times$ is not a square in $K$ and $\ch(K)\neq 2$. Then $x^2-r\in K[x]$ is irreducible and we have a quadratic extension of $K$ given by \[K[x]/(x^2-r)=K(\sqrt{r})=\left\{ a+b\sqrt{r} \;|\; a,b \in K\right\}\]

Well-studied examples are $\mathbb{Q}(\sqrt{2})/\mathbb{Q}$, $\mathbb{Q}(\sqrt{-3})/\mathbb{Q}$ and $\mathbb{C}/\mathbb{R}$ (which is just $\mathbb{R}(i)/\mathbb{R}$). These all live in the big field $\mathbb{C}$ which provides a ready-made source of roots of the polynomial $x^2-r$.

For an example where the previous section provides something new, consider the field of rational expressions $K=\mathbb{Q}(t)$ with indeterminate $t$. The element $t$ isn’t a square in $K$ and $f(x)=x^2-t$ is irreducible in $K[x]$. This has a root which we might as well call $\sqrt{t}$ and we obtain a quadratic extension of $K$ given by \[K(\sqrt{t})=\left\{ a+b\sqrt{t} \;|\; a,b \in K\right\}.\] Notice this is actually just $\mathbb{Q}(t)(\sqrt{t})=\mathbb{Q}(s)$, the field of rational expressions with coefficients in $\mathbb{Q}$ and an indeterminate $s$ satisfying $s^2=t$.

Another new example is a quadratic extension of $\mathbb{F}_3$. Notice that $2\in\mathbb{F}_3$ is not a square in $\mathbb{F}_3$ (and in fact it is the only non-square element). We obtain a quadratic extension of $\mathbb{F}_3$ by adjoining a root $\theta$ of the irreducible polynomial $f(x)=x^2-2$ \[\mathbb{F}_3[x]/(x^2-2)=\mathbb{F}_3(\theta)=\left\{ a+b\theta \;|\; a,b \in\mathbb{F}_3\right\}\] and every element can be written uniquely in the form $a+b\theta$ with $a,b\in\mathbb{F}_3$. In particular, it is a field with $9$ elements, which we call $\mathbb{F}_9$.

Explicitly, its elements are \[\mathbb{F}_9=\{0,\, 1,\, 2,\, \theta,\, 1+\theta,\, 2+\theta,\, 2\theta,\, 1+2\theta,\, 2+2\theta\}. \]
We add elements by remembering that $3=0$ in $\mathbb{F}_3$ so, for example, \[(1+\theta)+(2+\theta)=3+2\theta=2\theta.\]
We multiply elements by remembering that $\theta^2=2$ so, for example, \[(1+\theta)(2+\theta)=2+3\theta+\theta^2=1.\]
The $8$ non-zero elements have multiplicative inverses, for example $(1+\theta)^{-1}=2+\theta$.
Warning: $\mathbb{F}_9$ is not the same as $\mathbb{Z}/9$. The ring $\mathbb{Z}/9$ is not a field as it has zero divisors.
Later we will see that $\mathbb{F}_9$ is the unique field with $9$ elements (up to isomorphism).
Amusing fact: since $2=-1$ in $\mathbb{F}_3$, we have actually adjoined a square root of $-1$, so $\mathbb{F}_9/\mathbb{F}_3$ is analogous to the construction of $\mathbb{C}/\mathbb{R}$.

Now consider a quadratic extension of $\mathbb{F}_2$. Since $0=0^2$ and $1=1^2$, we have $\mathbb{F}_2(\sqrt{r})=\mathbb{F}_2$ for each $r\in\mathbb{F}_2$ so we can’t obtain a non-trivial extension by adjoining a square root. However, there is an irreducible quadratic polynomial, namely $f(x)=x^2+x+1\in\mathbb{F}_2[x]$ (and in fact it is the only one.) Letting $\theta$ be a root, we obtain a field \[\mathbb{F}_4=\mathbb{F}_2[x]/(x^2+x+1)=\mathbb{F}_2(\theta)=\left\{ a+b\theta \;|\; a,b \in\mathbb{F}_2\right\}\]

It has $4$ elements and $\mathbb{F}_4=\{0,\, 1,\, \theta,\, 1+\theta\}$.
We add elements by remembering that $2=0$ so, for example, $(1+\theta)+\theta=1$.
We multiply elements by remembering that $\theta^2=-\theta-1=\theta+1$, for example, \[\theta\cdot\theta=\theta+1,\quad\, \theta\cdot(\theta+1)=\theta^2+\theta=1,\quad \text{etc.}\]
Check that for each non-zero element $\alpha\in\mathbb{F}_4^\times$, we we have $\alpha^3=1$. This shouldn’t be so surprising since the non-zero elements in a field form an abelian group under multiplication. In this case, there are $3$ elements so this is isomorphic to the cyclic group of order $3$.
Warning: $\mathbb{F}_4$ is not the same as $\mathbb{Z}/4$. The ring $\mathbb{Z}/4$ is not a field as it has zero divisors.
Amusing fact: Notice that for each $\alpha\in\mathbb{F}_4$ (including zero) we have $\alpha^4=\alpha$. Compare this with Fermat’s Little Theorem 2.2 which stated $a^p=a$ for all $a\in\mathbb{F}_p$ when $p$ is prime.

Higher degrees

Adjoining an algebraic element of degree $n\geq 2$ to a field gives a simple extension in a similar way:

Proposition 3.3 Let $K(\theta)/K$ be a simple extension where $\theta$ is algebraic over $K$ with minimal polynomial $m(x)\in K[x]$ of degree $n$. Then \[K(\theta)=\left\{ c_0+c_1\theta+\cdots+c_{n-1}\theta^{n-1} \;|\; c_j\in K\right\}\] and the elements are written uniquely in this form, i.e. $K(\theta)$ is a vector space over $K$ of dimension $n$ with a basis $\{1,\theta,...,\theta^{n-1}\}$.

Proof. By Theorem 3.1 and Proposition 3.1, we can take $K(\theta)=K[x]/(m(x))$ where $\theta=\pi(x)$ and $\pi:K[x]\to K[x]/(m(x))$ is the canonical projection.

Since $\pi$ is surjective, every element of $K(\theta)$ equals $\pi(f(x))$ for some $f(x)\in K[x]$. The Division Algorithm says there are unique $q(x),r(x)\in K[x]$ such that $f(x)=q(x)m(x)+r(x)$ with $\deg r(x)<n$. So \[r(x)=c_0+c_1x+\cdots+c_{n-1}x^{n-1}\] where the $c_j\in K$ are uniquely determined. Finally, \[\pi(f(x))=\pi(r(x))=r(\theta)=c_0+c_1\theta+\cdots+c_{n-1}\theta^{n-1}\] where the $c_j$ are uniquely determined.

We’ve already seen an example: \[\mathbb{Q}(\sqrt[3]{2})=\left\{ a+b\sqrt[3]{2}+c\sqrt[3]{4} \;|\; a,b,c \in\mathbb{Q}\right\}.\] This is formed by adjoining the real root $\theta=\sqrt[3]{2}$ of the irreducible cubic $f(x)=x^3-2\in\mathbb{Q}[x]$ to $\mathbb{Q}$. It can also be defined abstractly by $\mathbb{Q}[x]/(x^3-2)$ using the methods of the previous section. But notice that $f(x)$ has 3 roots $\theta, \omega\theta, \omega^2\theta\in\mathbb{C}$ where $\omega=e^{2\pi i/3}$. We obtain fields \[\mathbb{Q}(\omega^j\theta)=\left\{ a+b\omega^j\theta+c\omega^{2j}\theta^2 \;|\; a,b,c \in\mathbb{Q}\right\}\] for $j=0,1,2$ which are different as subsets of $\mathbb{C}$. One of them is contained in the real numbers $\mathbb{R}$ but the other two aren’t. However, they are all isomorphic as abstract field extensions of $\mathbb{Q}$ since $\theta, \omega\theta, \omega^2\theta$ have the same minimal polynomial.

Now consider degree $3$ polynomials in $\mathbb{F}_2[x]$ and recall exactly two of them are irreducible, namely \[ f_1(x)=x^3+x+1\quad\text{and}\quad f_2(x)=x^3+x^2+1.\] If $\theta_j$ is a root of $f_j(x)$ for $j=1,2$, we apparently have two fields \[\mathbb{F}_2(\theta_i)=\left\{ a+b\theta_i+c\theta_i^2 \;|\; a,b,c \in\mathbb{F}_3\right\}\] each having $8$ elements. In fact, these are essentially the same field since there is a (unique) field isomorphism $\varphi:\mathbb{F}_2(\theta_1)\to\mathbb{F}_2(\theta_2)$ such that $\varphi(\theta_1)=\theta_2^{-1}$. (Exercise: check this by using the fact that $\theta_2^{-1}$ is a root of $f_1(x)$.)

Remark. Next term, we’ll see that when $q$ is a power of a prime, there is a (unique up to isomorphism) field $\mathbb{F}_q$ with $q$ elements. These finite fields are sometimes called Galois fields, in honour of the hero of our story.

3.5 Degrees of field extensions

We would like some way of measuring how big a given field extension is. We’ve already seen the idea in the last section where we considered simple extensions $K(\theta)/K$ as vector spaces over $K$. This works more generally, and for an arbitrary field extension $L/K$, we can consider $L$ as a vector space over $K$ in a natural way. Addition and subtraction are the same as in the field $L$ and scalar multiplication is multiplication of elements of $L$ by the “scalars” which are just the elements of $K\subset L$. It’s easy to check that this does satisfy the axioms of a vector space over $K$.

Remark. In other words, we are essentially “forgetting” how to multiply elements of $L$ that aren’t in $K$. This idea of forgetting some structure can be a surprisingly useful mathematical technique. We do it for instance, when we plot complex numbers in the plane $\mathbb{R}^2$. It’s just that in $\mathbb{C}$, we also have a special way of multiplying arbitrary complex numbers.

Definition 3.5 The degree of a field extension $L/K$ is the dimension of $L$ as a vector space over $K$, and is denoted by $[L:K]$.

Example 3.5 $(a)$ When $\theta$ is algebraic over $K$ of degree $n$, Proposition 3.3 says $[K(\theta):K]=n$ and $\{1,\theta,...,\theta^{n-1}\}$ is a basis. In particular, \[[\mathbb{C}:\mathbb{R}]=2,\quad [\mathbb{Q}(\sqrt{2}):\mathbb{Q}]=2,\quad[\mathbb{Q}(\sqrt[3]{2}):\mathbb{Q}]=3.\]

$(b)$ Consider the rational expressions $K(t)/K$ with coefficients in a field $K$ and indeterminate $t$. The elements $\{1,t,t^2,...\}$ are linearly independent so this vector space is infinite dimensional and we write $[K(t):K]=\infty$. In view of Proposition 3.2, if $\theta$ is transcendental over $K$, then $[K(\theta):K]=\infty$ as well.

To signify that an extension $L/K$ has finite degree, we’ll write $[L:K]<\infty$. This finiteness condition actually implies there are no transcendental elements. If every element in $L$ is algebraic over $K$ we call $L/K$ an algebraic extension and

Proposition 3.4 If $[L:K]<\infty$, then $L/K$ is an algebraic extension and $L=K(\alpha_1,...,\alpha_n)$ for some finite set of elements $\alpha_1,...,\alpha_n\in L$.

Proof. Suppose $[L:K]=n$ is finite. Then it has a finite basis $\alpha_1,...,\alpha_n$ and $L=K(\alpha_1,...,\alpha_n)$. Furthermore, any $n+1$ elements of $K$ must be linearly dependent over $K$. In particular, given $\theta\in L$, the $n+1$ elements $\{1,\theta,...,\theta^n\}$ must satisfy a non-trivial linear relationship \[c_0+c_1\theta+\cdots+c_n\theta^n=0\] with $c_i\in K$ not all zero. In other words, $\theta$ is a root of the non-zero polynomial \[f(x)=c_0+c_1x+\cdots+c_nx^n\in K[x]\] and hence every $\theta\in L$ is algebraic over $K$.

Remark. The converse of this result is also true and follows directly from the next Theorem. However, there are algebraic extensions of infinite degree (which necessarily can not generated by adjoining finitely many elements). A very interesting example is the field of all algebraic numbers over $\mathbb{Q}$ \[\overline{\mathbb{Q}}=\left\{\alpha\in\mathbb{C} \mid \text{$\alpha$ is algebraic over $\mathbb{Q}$}\right\}.\] It’s easy to construct arbitrarily many elements in here which are linearly independent over $\mathbb{Q}$. (E.g. consider $1,2^{1/n},2^{2/n},...,2^{(n-1)/n}$ for arbitrary fixed $n$.) What is not so easy is to show that $\overline{\mathbb{Q}}$ is a field. Try showing that if $\alpha,\beta$ are algebraic over $\mathbb{Q}$, then so are $\alpha\pm\beta$, $\alpha\beta$ and $\alpha/\beta$ (when $\beta\neq 0$). Without the next theorem, it’s really awkward.

Let’s consider extensions formed by adjoining multiple elements, i.e. an extension $K(\theta_1,...,\theta_r)/K$. It should be clear that $K(\theta_1,...,\theta_r)=K(\theta_1)(\theta_2)...(\theta_r)$ and we can iteratively use the following very useful fact.

Theorem 3.2 (Tower Law) Let $K\subset M\subset L$ be field extensions.

$\;\;(i)\;\;[L:K]<\infty\iff[L:M]<\infty$ and $[M:K]<\infty$.

$\;(ii)$ $[L:K]=[L:M][M:K]$

Proof. We claim the following: if $\{\alpha_i \mid i\in I \}$ is a basis of $M/K$ and $\{\beta_j\mid j\in J\}$ is a basis of $L/M$, then $\{\alpha_i\beta_j\; \mid i\in I, j\in J \}$ is a basis of $L/K$. The result follows by counting elements in these bases.

To prove the claim, first check that any $\gamma\in L$ is in the span of $\{\alpha_i\beta_j\; \mid i\in I, j\in J \}$.

$\{\beta_j\mid j\in J\}$ spans $L/M$ so there are $c_j\in M$ such that $\displaystyle\gamma=\sum_{j} c_j\beta_j$.
$\{\alpha_i \mid i\in I \}$ spans $M/K$ so there are $d_{ij}\in K$ such that $\displaystyle c_j=\sum_{i} d_{ij}\alpha_i$ for each $j$.
Combining shows $\displaystyle\gamma=\sum_{i,j} d_{ij}\alpha_i\beta_j$ is in the span of $\{\alpha_i\beta_j\; \mid i\in I, j\in J \}$.

For linear independence, suppose $\displaystyle\sum_{i,j} d_{ij}\alpha_i\beta_j=0$ for some $d_{ij}\in K$.

Write $\displaystyle e_j=\sum_{i} d_{ij}\alpha_i\in M$, so that $\displaystyle\sum_{j} e_j\beta_j=0$.
$\{\beta_j\mid j\in J\}$ is linearly independent over $M$ so $e_j=0$, i.e. $\displaystyle\sum_{i} d_{ij}\alpha_i=0$ for each $j$.
$\{\alpha_i \mid i\in I \}$ is linearly independent over $K$ so $d_{ij}=0$ for each $i,j$.

Example 3.6 $(a)$ Let’s check explicitly how this is working in the case \[K=\mathbb{Q}\;\;\;\subset\;\;\; M=\mathbb{Q}\left(\sqrt{2}\right)\;\;\;\subset\;\;\; L=\mathbb{Q}\left(\sqrt{2},\sqrt{7}\right).\]

We already know $M=\left\{a+b\sqrt{2} \mid a,b\in\mathbb{Q}\right\}$ and $[M:K]=2$.
For the extension $L/M$, we adjoin the root $\sqrt{7}$ of $f(x)=x^2-7$. Now, $f(x)$ is clearly irreducible over $\mathbb{Q}$ but we need to know its irreducibility over $M=\mathbb{Q}(\sqrt{2})$. We check this by showing that it has no roots in $M$. Suppose $c+d\sqrt{2}\in\mathbb{Q}(\sqrt{2})$ and $(c+d\sqrt{2})^2=7$. Then \[\begin{align*} (c^2+2d^2)+2cd\sqrt{2}=7 \quad &\implies\quad c^2+2d^2=7 \;\;\text{and}\;\;2cd=0 \\ \quad &\implies\quad c=0,\;d^2=7/2 \;\;\text{or}\;\; d=0,\;c^2=7. \end{align*}\] This is clearly impossible for $c,d\in\mathbb{Q}$ and we have $[L:M]=2$.
Finally, \[\begin{align*} L&=\left\{\alpha+\beta\sqrt{7} \mid \alpha,\beta\in M\right\} =\left\{ a+b\sqrt{2}+c\sqrt{7}+d\sqrt{14} \mid a,b,c,d\in\mathbb{Q} \right\} \end{align*}\] and elements are uniquely expressible as $a+b\sqrt{2}+c\sqrt{7}+d\sqrt{14}$. This implies $[L:K]=4$.

$(b)$ Let $L=\mathbb{Q}\left(\sqrt{2},\sqrt[3]{15}\right)$, then we can use the Tower Law to show $[L:\mathbb{Q}]=6$.

Both $x^2-2$ and $x^3-15$ are irreducible in $\mathbb{Q}[x]$, so $[\mathbb{Q}(\sqrt{2}):\mathbb{Q}]=2$ and $[\mathbb{Q}(\sqrt[3]{15}):\mathbb{Q}]=3$.
But $\mathbb{Q}(\sqrt{2})$ and $\mathbb{Q}(\sqrt[3]{15})$ are subfields of $L$ so the Tower Law implies $[L:\mathbb{Q}]$ is divisible by $2$ and $3$, hence is divisible by $6$.
On the other hand, $\mathbb{Q}\subset\mathbb{Q}(\sqrt{2})\subset L$ and $[L:\mathbb{Q}(\sqrt{2})]\leq 3$ so $[L:\mathbb{Q}]\leq 2\times 3=6$. Hence we’ve found $[L:\mathbb{Q}]=6$. Notice that this means we actually have $[L:\mathbb{Q}(\sqrt{2})]=3$ so $x^3-15$ is irreducible in $\mathbb{Q}(\sqrt{2})[x]$. Similarly, $x^2-2$ is irreducible in $\mathbb{Q}(\sqrt[3]{15})[x]$.

$(c)$ Let $L=\mathbb{Q}\left(\sqrt[3]{7},\sqrt[5]{7}\right)$. Then $[L:\mathbb{Q}]=15$.

This follows as above: $[\mathbb{Q}(\sqrt[3]{7}):\mathbb{Q}]=3$ and $[\mathbb{Q}(\sqrt[5]{7}):\mathbb{Q}]=5$ are coprime and we find $[L:\mathbb{Q}]=15$.
This could also be seen by noticing that $L=\mathbb{Q}\left(\sqrt[15]{7}\right)$. Indeed, let $\theta=\sqrt[15]{7}$. Then $\theta^5=\sqrt[3]{7}$ and $\theta^3=\sqrt[5]{7}$ so $L\subset\mathbb{Q}(\theta)$. On the other hand, $\theta=(\theta^3)^2/\theta^5$ so $\mathbb{Q}(\theta)\subset L$.

The following two simple consequences of the Tower Law are often useful:

If $K\subset M\subset L$, then $[M:K]$ and $[L:M]$ both divide $[L:K]$.
For $\alpha,\beta$ algebraic over $K$, we have \[[K(\alpha,\beta):K]\leq [K(\alpha):K] [K(\beta):K].\] Indeed, consider the minimal polynomial $m(x)$ of $\alpha$ over $K$ and the minimal polynomial $m_1(x)$ of $\alpha$ over $K(\beta)$. These might not be equal, but we do know that $m(x)\in K[x]\subset K(\beta)[x]$ vanishes at $\alpha$ so $m_1(x)|m(x)$. In particular, \[[K(\alpha,\beta):K(\beta)]=\deg m_1(x)\leq\deg m(x)=[K(\alpha):K].\]

Computing minimal polynomials

We’ll end the chapter with a series of computations of minimal polynomials, using everything we know about degrees.

$(a)$ Find the minimal polynomial of $\theta=\sqrt{2}-1$ over $\mathbb{Q}$.

We have $\mathbb{Q}(\theta)=\mathbb{Q}(\sqrt{2})$ which has degree $2$ over $\mathbb{Q}$, so the minimal polynomial has degree $2$.
Now $(\theta+1)^2=2\;\implies\;\theta^2+2\theta-1=0$ so the minimal polynomial is $x^2+2x-1$.

$(b)$ Find the minimal polynomial of $\theta=1+\sqrt[3]{4}$ over $\mathbb{Q}$.

We have $\mathbb{Q}(\theta)=\mathbb{Q}(\sqrt[3]{4})$ which has degree $3$ over $\mathbb{Q}$, so the minimal polynomial has degree $3$.
Now $(\theta-1)^3=4\;\implies\;\theta^3-3\theta^2+3\theta-5=0$ so the minimal polynomial is $x^3-3x^2+3x-5$.

$(c)$ Find the minimal polynomial of $\theta=\sqrt{2}+\sqrt{7}$ over $\mathbb{Q}(\sqrt{2})$.

Notice $\mathbb{Q}(\sqrt{2})(\theta)=\mathbb{Q}(\sqrt{2},\sqrt{7})$, which we already saw has degree $2$ over $\mathbb{Q}(\sqrt{2})$. So the minimal polynomial has degree $2$.
Now $\theta-\sqrt{2}=\sqrt{7}\;\implies\;(\theta-\sqrt{2})^2=7\;\implies\;\theta^2-2\sqrt{2}\theta-5=0$ so the minimal polynomial over $\mathbb{Q}(\sqrt{2})$ is $x^2-2\sqrt{2}x-5$.

$(d)$ Find the minimal polynomial of $\theta=\sqrt{2}+\sqrt{7}$ over $\mathbb{Q}$.

Since $\mathbb{Q}\subset\mathbb{Q}(\theta)\subset\mathbb{Q}(\sqrt{2},\sqrt{7})$, the degree of the minimal polynomial, i.e. $[\mathbb{Q}(\theta):\mathbb{Q}]$ divides $[\mathbb{Q}(\sqrt{2},\sqrt{7}):\mathbb{Q}]=4$ so is $1$, $2$ or $4$.
The degree is not $1$. If it was, then we would have $\theta\in\mathbb{Q}$.
The degree is not $2$. If it was, then $1,\theta,\theta^2$ would be linearly dependent over $\mathbb{Q}$. But \[\begin{align*} c_0+c_1\theta+c_2\theta^2=0 \quad &\implies\quad (c_0+9c_2)+c_1\sqrt{2}+c_1\sqrt{7}+2c_2\sqrt{14}=0 \\ \quad &\implies\quad c_0=c_1=c_2=0. \end{align*}\]
Hence the degree is $4$. To find the minimal polynomial explicitly, eliminate the irrationalities as follows \[\begin{align*} \theta^2=(\sqrt{2}+\sqrt{7})^2=9+2\sqrt{14} \quad &\implies\quad (\theta^2-9)^2=56 \\ \quad &\implies\quad \theta^4-18\theta^2+25=0 \end{align*}\] and the minimal polynomial is $x^4-18x^2+25$. Notice this factorises as $(x^2-2\sqrt{2}x-5)(x^2+2\sqrt{2}x-5)$ in $\mathbb{Q}(\sqrt{2})[x]$ and compare with example $(c)$.
Something interesting has happened here. We’ve found $\mathbb{Q}(\theta)\subset\mathbb{Q}(\sqrt{2},\sqrt{7})$, and $\mathbb{Q}(\theta)$ and $\mathbb{Q}(\sqrt{2},\sqrt{7})$ are vector spaces of the same dimension. That means they are equal so \[\mathbb{Q}(\sqrt{2},\sqrt{7})=\mathbb{Q}(\sqrt{2}+\sqrt{7})\] is actually a simple extension! We could prove this directly by showing $\sqrt{2},\sqrt{7}\in\mathbb{Q}(\theta)$. This can be done in many ways by multiplying elements to construct linear combinations. For instance, \[\begin{align*} \theta^3&=2\sqrt{2}+3\cdot 2\cdot\sqrt{7}+3\cdot\sqrt{2}\cdot 7+7\sqrt{7} \\ &= 23\sqrt{2}+13\sqrt{7} =\begin{cases} \;\;\,10\sqrt{2}+13\theta \;\;\implies\;\; \sqrt{2}=(\theta^3-13\theta)/10 \\ -10\sqrt{7}+23\theta \;\;\implies\;\; \sqrt{7}=(23\theta-\theta^3)/10 \end{cases} \end{align*}\] Surprisingly many field extensions are simple, even if they don’t appear so at first. In fact, one can show that if $K$ has characteristic zero, then every finite extension $L/K$ is simple. (This is a special case of the Theorem of the Primitive element.)

Finally, considering degrees give a slick way to prove the set of algebraic numbers $\overline{\mathbb{Q}}$ is a subfield of $\mathbb{C}$.

First notice $\overline{\mathbb{Q}}=\left\{\alpha\in\mathbb{C} \;\mid\; [\mathbb{Q}(\alpha):\mathbb{Q}]<\infty\right\}$.
For $\alpha,\beta\in\overline{\mathbb{Q}}$, we have $\alpha+\beta\in \mathbb{Q}(\alpha,\beta)$ so $\mathbb{Q}(\alpha+\beta)\subset\mathbb{Q}(\alpha,\beta)$.
Then $[\mathbb{Q}(\alpha+\beta):\mathbb{Q}] \leq [\mathbb{Q}(\alpha,\beta):\mathbb{Q}] \leq [\mathbb{Q}(\alpha):\mathbb{Q}] [\mathbb{Q}(\beta):\mathbb{Q}]<\infty$ and so $\alpha+\beta\in\overline{\mathbb{Q}}$.
Similarly, we obtain $-\alpha\in\overline{\mathbb{Q}}$, $\alpha\beta\in\overline{\mathbb{Q}}$ and $\alpha/\beta\in\overline{\mathbb{Q}}$ (when $\beta\neq 0$).