6 SL₂ 6.2 Classification of representations of sl_2,C.6.4 Real forms and complete decomposability

6.3 Decomposing representations

Theorem 6.19.

Let $V$ be any finite-dimensional complex-linear representation of $\mathfrak{sl}_{2,\mathbb{C}}$ . Then $V$ is completely reducible, that is, splits into a direct sum of irreducible representations.

Proof.

We will prove this later (Theorem 6.30) using the compact Lie group $\mathrm{SU}(2)$ . ∎

It is easy to decompose a representation $V$ of $\mathfrak{sl}_{2,\mathbb{C}}$ into irreducibles by looking at the weights. Firstly, look at the maximal weight $k$ of $V$ . Then there must be a weight vector $v$ of weight $k$ , which is necessarily a highest weight vector, and so $V$ must contain a copy of $\operatorname{Sym}^{k}(\mathbb{C}^{2})$ — namely, the subspace $\left\langle v,Yv,\ldots,Y^{k}v\right\rangle$ . By complete reducibility we have

V\cong\operatorname{Sym}^{k}(\mathbb{C}^{2})\oplus W.

The weights of $W$ are then obtained by removing the weights of $\operatorname{Sym}^{k}(\mathbb{C}^{2})$ from the weights of $V$ , and we repeat the process.

In particular, this shows that a finite-dimensional representation of $\mathfrak{sl}_{2,\mathbb{C}}$ is determined, up to isomorphism, by its multiset of weights.

Proposition 6.20.

If $V$ , $W$ are representations of $\mathfrak{sl}_{2,\mathbb{C}}$ then:

•

$\{$ weights of $V\otimes W\}=\{$ weights of $V\}+\{$ weights of $W\}$ .
•

$\{$ weights of $\operatorname{Sym}^{k}(V)\}=\{$ sums of unordered $k$ -tuples of weights of $V\}$ .
•

$\{$ weights of $\Lambda^{k}(V)\}=\{$ sums of unordered ‘distinct’ $k$ -tuples of weights of $V\}$ .

Proof.

Omitted: try it yourself! For a similar result, see section 7.5 below. ∎

Example 6.21.

We should illustrate what is meant by ‘distinct’: it is ‘distinct’ as elements of the multiset. Suppose that the weights of $V$ are $\{2,0,0,-2\}$ . Then to obtain the weights of $\Lambda^{2}(V)$ we add together unordered, distinct, pairs of these in every possible way, getting:

\{2+0,2+0,2+-2,0+0,0+-2,0+-2\}=\{2,2,0,0,-2,-2\}.

Example 6.22.

Let $\mathbb{C}^{2}$ be the standard representation of $\operatorname{SL}_{2}(\mathbb{C})$ with weight basis $e_{1}$ , $e_{-1}$ . Consider $V=\operatorname{Sym}^{2}(\mathbb{C}^{2})\otimes\operatorname{Sym}^{2}(\mathbb{% C}^{2})$ . Let $v_{2}=e_{1}^{2}$ , $v_{0}=e_{1}e_{-1}$ and $v_{-2}=e_{-1}^{2}$ be weight vectors in $\operatorname{Sym}^{2}(\mathbb{C}^{2})$ corresponding to the weights $2$ , $0$ and $-2$ . Then the weights of $V$ are

•

$4$ , multiplicity one, weight vector: $v_{2}\otimes v_{2}$ .
•

$2$ , multiplicity two, weight space: $\left\langle v_{2}\otimes v_{0},v_{0}\otimes v_{2}\right\rangle$ .
•

$0$ , multiplicity three, weight space: $\left\langle v_{2}\otimes v_{-2},v_{0}\otimes v_{0},v_{-2}\otimes v_{2}\right\rangle$ .
•

$-2$ , multiplicity two, weight space: $\left\langle v_{0}\otimes v_{-2},v_{-2}\otimes v_{0}\right\rangle$ .
•

$-4$ , multiplicity one, weight vector: $\left\langle v_{-2}\otimes v_{-2}\right\rangle$ .

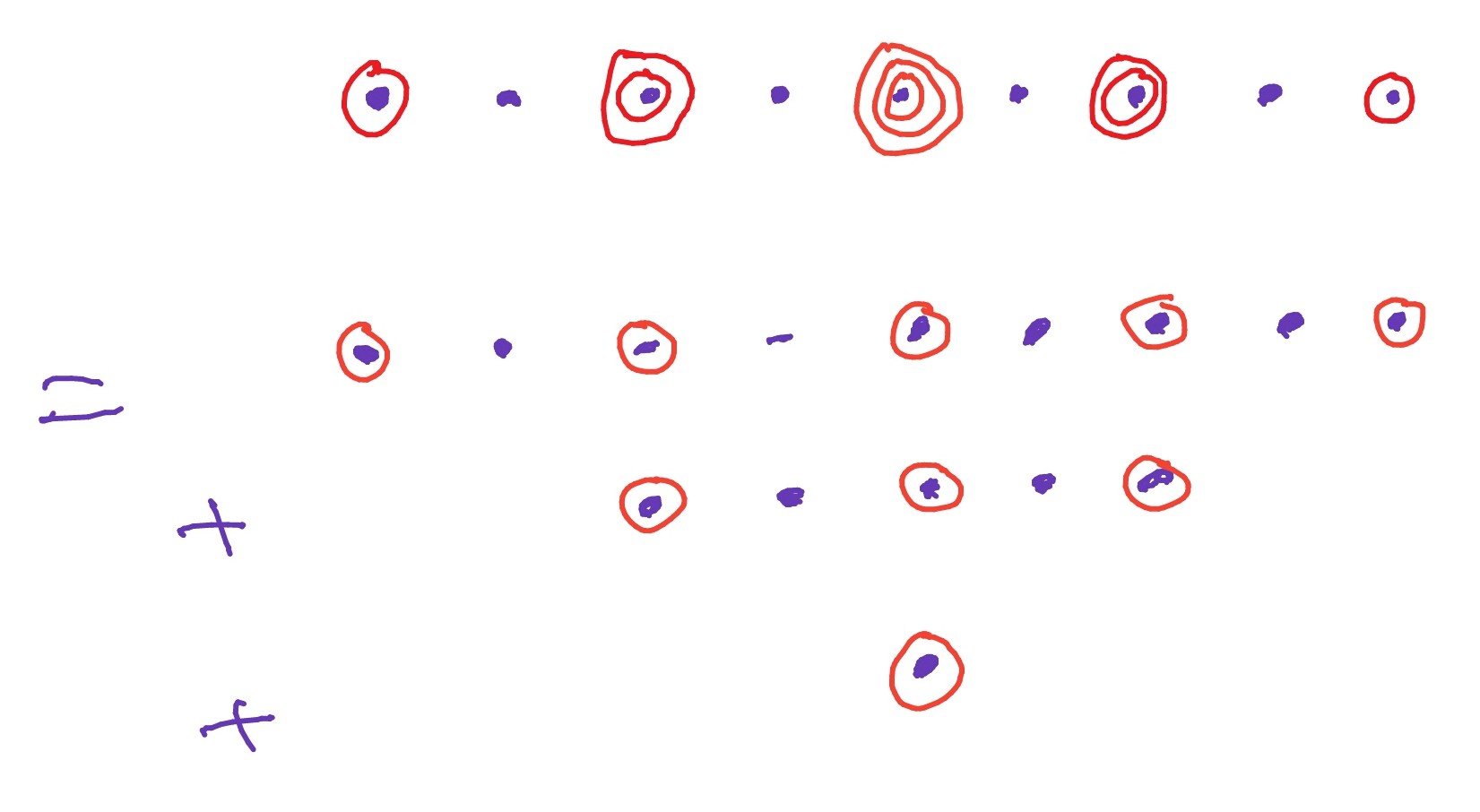
Figure 6: Decomposing $\operatorname{Sym}^{2}(\mathbb{C}^{2})\otimes\operatorname{Sym}^{2}(\mathbb{C}% ^{2})$ .

The weights of $\operatorname{Sym}^{2}(\mathbb{C}^{2})$ are $\{-2,0,2\}$ and so the weights of $V\otimes V$ are

\{-2,0,2\}+\{-2,0,2\}=\{-4,-2,-2,0,0,0,2,2,4\}.

This is the same as the set of weights of

\operatorname{Sym}^{4}(\mathbb{C}^{2})\oplus\operatorname{Sym}^{2}(\mathbb{C}^% {2})\oplus\mathbb{C}

and so this is the required decomposition into irreducibles.

We can go further, and decompose $V$ into irreducible *sub*representations. This means finding irreducible subrepresentations of $V$ such that $V$ is their direct sum.

The copy of $\operatorname{Sym}^{4}(\mathbb{C}^{2})$ in $V$ has highest weight vector $v_{2}\otimes v_{2}$ . We can find a basis by repeatedly hitting this with $Y$ (writing $\propto$ for ‘equal up to a nonzero scalar’):

	$\displaystyle Y(v_{2}\otimes v_{2})$	$\displaystyle=2(v_{2}\otimes v_{0}+v_{0}\otimes v_{2})\propto v_{2}\otimes v_{% 0}+v_{0}\otimes v_{2}$
	$\displaystyle Y^{2}(v_{2}\otimes v_{2})$	$\displaystyle\propto v_{2}\otimes v_{-2}+4v_{0}\otimes v_{0}+v_{-2}\otimes v_{2}$
	$\displaystyle Y^{3}(v_{2}\otimes v_{2})$	$\displaystyle\propto 6(v_{0}\otimes v_{-2}+v_{-2}\otimes v_{0})\propto v_{0}% \otimes v_{-2}\otimes v_{-2}\otimes v_{0}$
	$\displaystyle Y^{4}(v_{2}\otimes v_{2})$	$\displaystyle\propto v_{-2}\otimes v_{-2}.$

These vectors are a basis for the copy of $\operatorname{Sym}^{4}(\mathbb{C}^{2})$ in $V$ .

Next, we find the copy of $\operatorname{Sym}^{2}(\mathbb{C}^{2})$ in $V$ . We start by looking for a highest weight vector of weight 2:

v_{2}\otimes v_{0}-v_{0}\otimes v_{2}

does the trick. Hitting this with $Y$ gives $v_{2}\otimes v_{-2}-v_{-2}\otimes v_{2}$ , and doing so again gives $v_{-2}\otimes v_{0}-v_{0}\otimes v_{-2}$ (up to scalar). These vectors are a basis for the copy of $\operatorname{Sym}^{2}(\mathbb{C}^{2})$ in $V$ .

Finally, we find the trivial representation $\mathbb{C}$ in $V$ . We need only find a weight vector of weight 0 which is killed by $X$ , and

v_{2}\otimes v_{-2}-2v_{0}\otimes v_{0}+v_{-2}\otimes v_{2}

does the job: this vector spans a copy of the trivial representation.