5  Questions for Chapter 5

5.1 Warm-up

Exercise 5.1 The diagrams below represent systems with components that fail independently: the probability that component \(i\) works is \(p_i \in [0,1]\). For each system: i. find the probability that the system works, as a function of \(p_1\), \(p_2\), and \(p_3\); ii. find the probability that the system works in case \(p_1 = p_2 = p_3 = 0.7\); iii. find the conditional probability that component \(1\) works, given that the system works, in case \(p_1 =p_2 = p_3 =0.7\).

(a) Two components in series
(b) Three components in parallel
(c) A system with four components
Figure 5.1

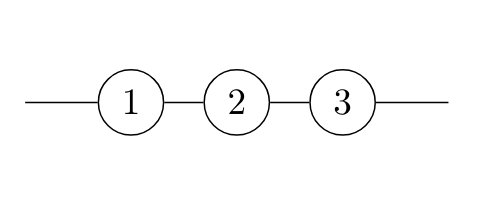
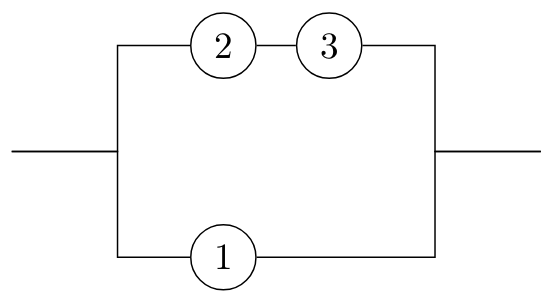
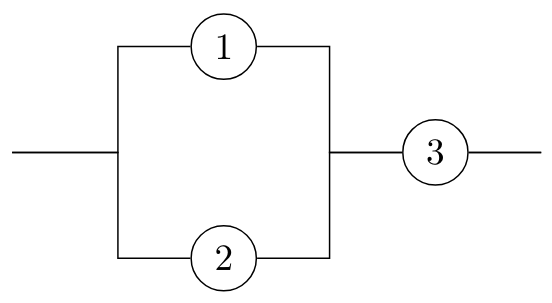
5.2 Workout

Exercise 5.2 The colour of a certain kind of mouse is determined by the inheritance of allele pairs of a gene, which are denoted BB, Bb and bb. B is dominant (BB or Bb give a black mouse, while bb gives a brown mouse). When mating, each parent passes one of its allele pair (each choice being equally likely) independently for each offspring.

In a certain experiment, two mice of type Bb are mated to produce an offspring, Mickey.

  1. Find the probability that Mickey is black.

For parts (b)–(d) suppose that Mickey is indeed black.

  1. What is the probability that Mickey is type BB?

  2. Mickey is mated with a brown mouse. They have three offspring. Find the probability that all the offspring are black.

  3. Suppose that all three offspring of part (c) are indeed black. What is the probability now that Mickey is of type BB?

  4. Finally, suppose that in the original experiment the genotypes of Mickey’s parents are unknown. However, each of the two mice, independently, has probability 1/3 of genotype BB, and probability 2/3 of genotype Bb.

Repeat parts (a), (b), (c) and (d) using this information.

Exercise 5.3 Suppose a (homologous) gene has two alleles A and a, of which a is recessive and also harmful, so aa individuals have some genetic disorder. Suppose the proportion of individuals of genotype Aa in the healthy population (i.e. those not of type aa) is \(\lambda\). Suppose a married couple, assumed to have come together by random mate selection, are both healthy. Suppose they have one healthy child. If they then decide to have a second child, what is the probability that it will also be healthy:

  1. as a function of \(\lambda\), and

  2. in the special case \(\lambda=0.1\).

5.3 Stretch

Exercise 5.4 The diagram below represents a system with components that fail independently. Suppose that component \(i\) works with probability \(\mathbb{P} ( W_i ) = p_i\). Find the probability that the system works as a function of \(p_1, \ldots, p_5\).

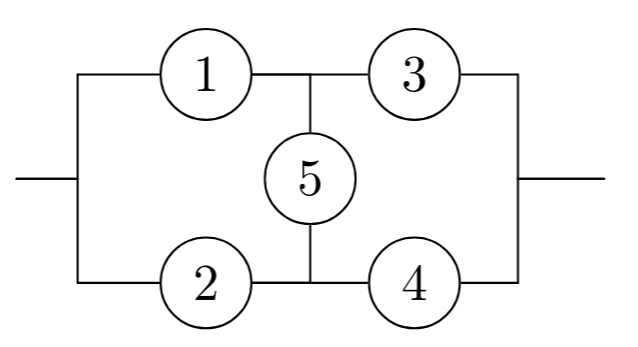
Figure 5.2: A system with five components

hint: Use the partition theorem with \(\{W_5,W_5^\mathrm{c}\}\)

Exercise 5.5 Suppose that a certain sex-linked gene has genotypes AA, Aa, aa in females, and genotypes A, a in males. Suppose that, for a particular generation, the genotypes AA, Aa, aa occur with frequencies \(u, 2v, w.\) Let \[p = u+v, \qquad q = v+w\] (so that \(p\), \(q\) with \(p + q = 1\) are the proportions of A and a in the female population). Suppose that the frequencies of the two genotypes A, a in the male population are \(p'\), \(q'\) (where \(p' + q' =1\)).

Assume random mating between males and females in a large population. Remember that, for a sex-linked gene, the son receives one gene from the mother and none from the father. Let \(p_1\), \(q_1\) be the proportions of A, a in females of the next generation, and let \(p'_1\), \(q'_1\) be the proportion of A, a in males of the next generation.

Show that \[p'_1 - p_1 =\frac{p-p'}{2} \quad\mbox{and}\quad \frac{2}{3}\, p_1 + \frac{1}{3}\, p'_1 = \frac{2}{3}\, p + \frac{1}{3}\, p'.\] Interpret these results.