Introduction

 

Consider the collection , and suppose that we take a sample of size over this collection. Let be the observation on , and collect the observations into the vector . Collect all the quantities together into the collection . Suppose that we might observe . (Actual observations are not essential.) The following expectations and covariances summarise our requirements for second-order exchangeability:

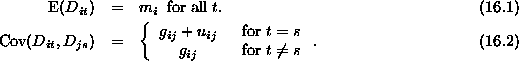
Arrange the and as the entries of the matrices , .

Such representations follow by explicitly writing the observation on the quantity

as the sum of a mean component plus a residual component, where the residual components are uncorrelated with all other quantities. In principle, we can now specify

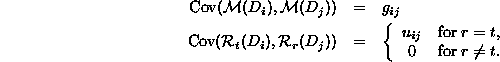
Then the variance matrix for the vector of averages

is . This variance matrix is coherent if both G and U are nonnegative definite.

In the context of the specifications one might actually make, it is often more natural to specify G and G+U, rather than G and U. This follows because is the variance of a typical member of the exchangeable sequence. It is for this reason that the commands involving exchangeable sequences typically demand that there are two belief stores, one containing G and the other G+U, pointed to by the modelvar  and infovar  controls respectively.

Various operators can be used to generate output related to exchangeable adjustments. See §21.4 for details.