The bearing is a quantity which summarises the actual effects of adjustment. Its principal properties are that
having the largest
standardised squared change in expectation; is equal to
the prior covariance between the quantity and the bearing;
The bearing for this adjustment is the linear combination
or, standardising the 
's,
We noted above the property that the changes from prior expectation to
adjusted expectation for quantities in 
are equivalent to the
covariances of the quantities with the bearing. For example, for
,
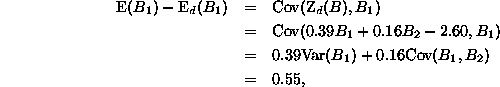
can be seen to be the difference between its expectation
and its adjusted expectation 
.
In this way, changes in expectation are expressible solely through a
covariance with the bearing, and so the magnitude of a change in
expectation for any quantity depends only upon the strength of
correlation between the quantity and the bearing, and upon the length
(i.e. the variance) of the bearing.
The variance of the bearing is a quantity that we refer to as the size of the adjustment. Here it is
We define the expected size of the adjustment to be the prior
expectation (where we replace 
by 
) for the size
of the adjustment. For our example, it is
We can show that the size of the adjustment always turns out to be equal
to the resolved uncertainty for the belief structure, 
, as
seen in section 4.3. In this sense we have that the
expected magnitude of change in expectation is equal to the expected
reduction in uncertainty over the entire base.
The ratio of the size of the adjustment to its expected size is termed the size ratio. Its value here is
We interpret the three size statistics as follows. The size of the
adjustment (here equal to 0.3179) summarises the magnitude of actual
change over the entire belief structure 
. Relative to its prior
variance, every linear combination in has an actual squared
change in expectation no greater than this value. For example, we can
be sure that the actual change in expectation in the quantity
is bounded according to
where 
. (In fact the actual change in expectation
turns out to be rather close to this bound, being
.) We contrast the value for the size of the
adjustment to its expectation by calculating their ratio, the size
ratio. For our example the value is 0.9389, very close to its
expectation of unity. Generally, the magnitude of the size ratio serves
as a further diagnostic test: a size ratio distant from unity may cause
us to reconsider our specifications, or to check our data values for
spurious entries, and so forth.