Recurrence and rates of convergence
Recall that the total variation distance between two probability distributions \(\mu\) and \(\nu\) on \(\mathcal{X}\) is given by \[\text{dist}_{\text{TV}}(\mu, \nu) \;=\; \sup_{A \subseteq \mathcal{X}}\{\mu(A)-\nu(A)\}\,.\] Show that this is equivalent to the distance (note the absolute value signs!) \[\sup_{A \subseteq \mathcal{X}}|\mu(A)-\nu(A)|\,.\]
Show that if \(\mathcal{X}\) is discrete, then \[\text{dist}_{\text{TV}}(\mu, \nu) = \tfrac12 \sum_{y\in\text{X}}|\mu(y)-\nu(y)|\,.\] (Here we do need to use the absolute value on the RHS!)
Hint: consider \(A=\{y: \mu(y)>\nu(y)\}\).Suppose now that \(\mu\) and \(\nu\) are density functions on \(\mathbb{R}\). Show that \[\text{dist}_{\text{TV}}(\mu, \nu) = 1 - \int_{-\infty}^\infty \min\{\mu(y),\nu(y)\} dy \,.\] Hint: remember that \(|\mu-\nu| = \mu+\nu - 2\min\{\mu,\nu\}\).
Consider a Markov chain \(X\) with continuous transition density kernel. Show that it possesses many small sets of lag 1.
Consider a Vervaat perpetuity \(X\), where \[X_0=0; \qquad X_{n+1} = U_{n+1}(X_n+1) \,,\] and where \(U_1,U_2,\dots\) are independent Uniform\((0,1)\) (simulated below).
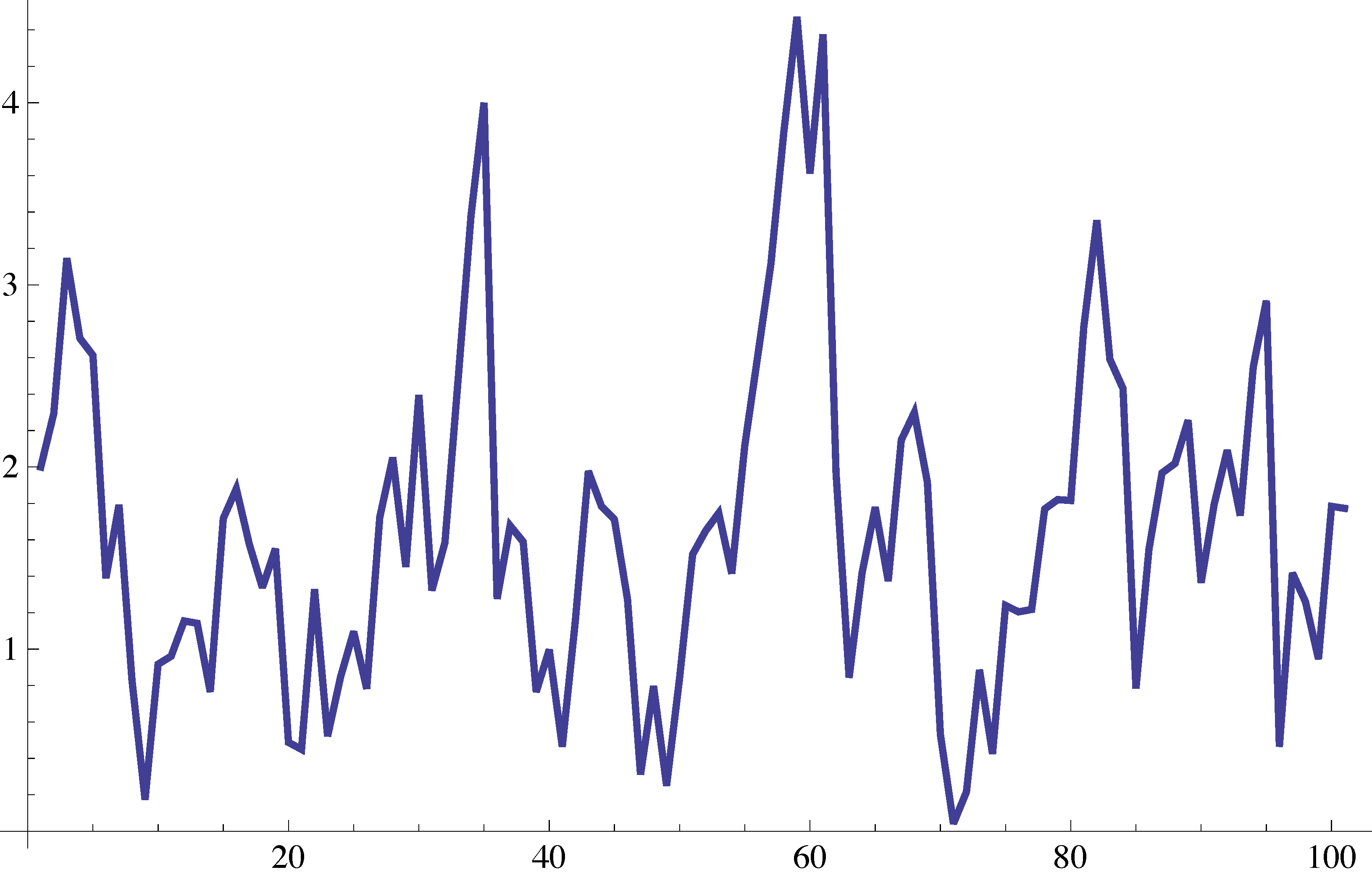
Find a small set for this chain.
- Recall the idea of regenerating when our chain hits a small set: suppose that \(C\) is a small set for a \(\phi\)-irreducible chain \(X\), i.e. for \(x \in C\),
\[\operatorname{\mathbb{P}}\left(X_1\in A| X_0=x\right) \geq \alpha \nu(A).\]
Suppose that \(X_n\in C\). Then with probability \(\alpha\) let \(X_{n+1} \sim \nu\), and otherwise let it have transition distribution
\(\tfrac{p(x,\cdot)-\alpha\nu(\cdot)}{1-\alpha}\).
- Check that the latter expression really gives a probability distribution.
- Check that \(X_{n+1}\) constructed in this manner obeys the correct transition distribution from \(X_n\).
- Define a reflected random walk as follows: \(X_{n+1}=\max\{X_n+Z_{n+1},0\},\) for \(Z_1, Z_2, \ldots\) i.i.d. with continuous density \(f(z)\), \[ \operatorname{\mathbb{E}}\left[Z_{1}\right]<0 \quad\text{and}\quad \operatorname{\mathbb{P}}\left(Z_{1}>0\right)>0 \,. \] Show that the Foster-Lyapunov criterion for positive recurrence holds, using \(\Lambda(x)=x\).