7 SL₃ 7.2 Weights 7.4 Representations and weights

7.3 Visualising weights

Shortly we will prove that, if $(\rho,V)$ is a finite dimensional representation of $\mathfrak{sl}_{3,\mathbb{C}}$ , then its weights are integer linear combinations of the $L_{i}$ . In other words, they lie in the weight lattice

\Lambda_{W}=\{a_{1}L_{1}+a_{2}L_{2}+a_{3}L_{3}:a_{1},a_{2},a_{3}\in\mathbb{Z}\}.

Exercise 7.10.

Show that $a_{1}L_{1}+a_{2}L_{2}+a_{3}L_{3}\in\Lambda_{W}$ if and only if $a_{1}-a_{2},a_{2}-a_{3}\in\mathbb{Z}$ . Must the $a_{i}$ be integers?

We want to visualise this in a way that treats $L_{1},L_{2},L_{3}$ symmetrically. Noticing that they sum to zero, we regard them them as the position vectors of the vertices an equilateral triangle with unit side length, centred on the origin. The weight lattice $\Lambda_{W}$ is then the set of vertices of equilateral triangles tiling the plane. For any representation $(\rho,V)$ , its weight diagram is then obtained by circling the weights that occur in that representation.

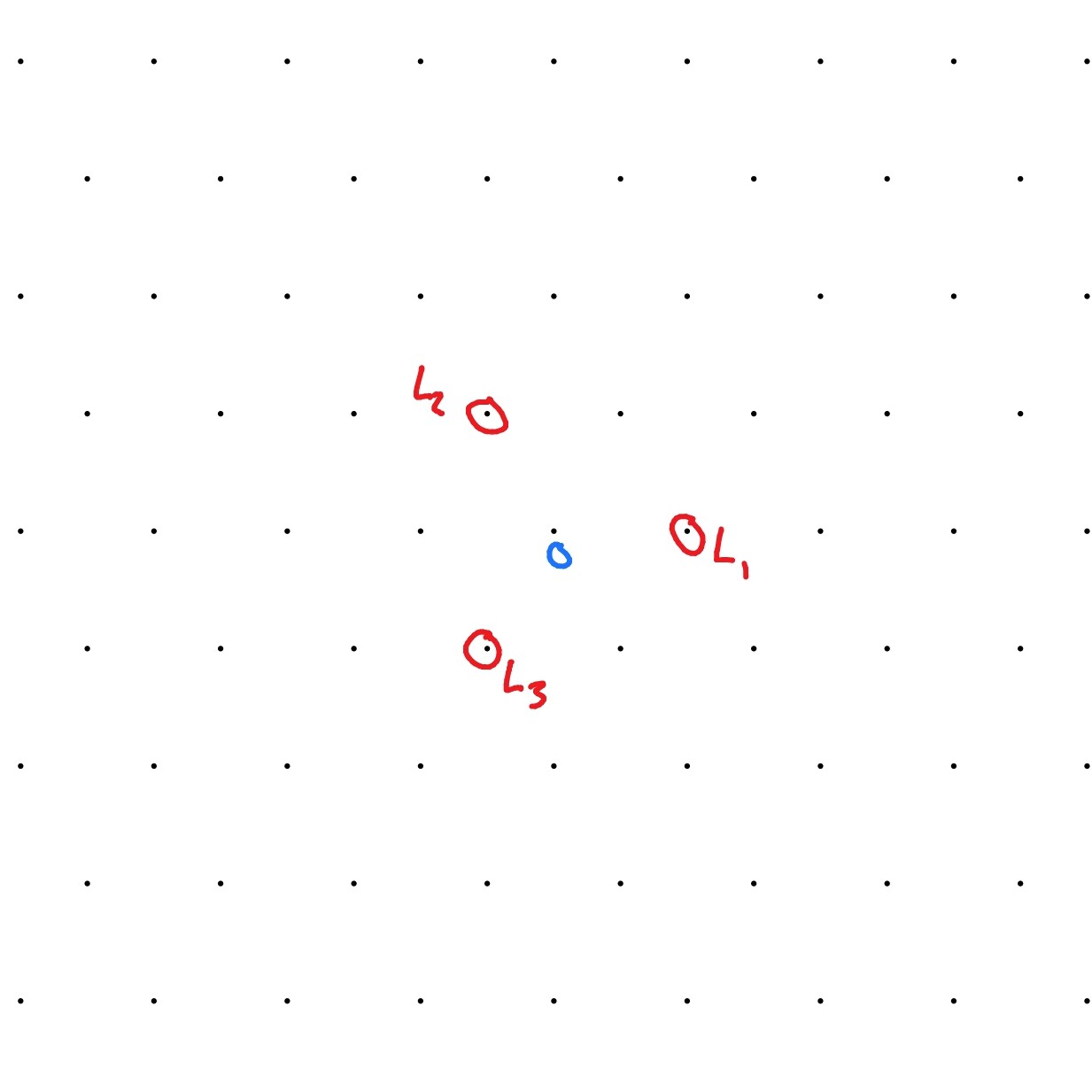
Example 7.11.

We draw the weight diagram for the standard representation, in Figure 7.

Figure 7: Weights for $\mathbb{C}^{3}$ .

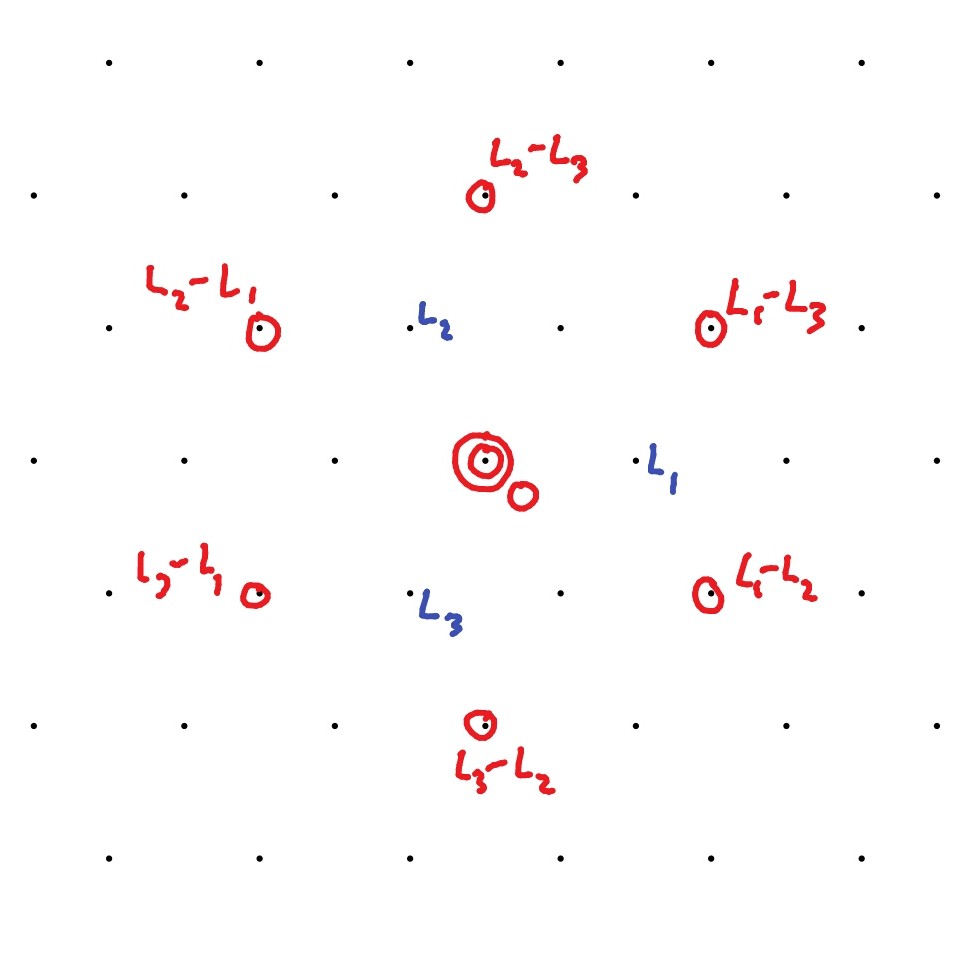
Example 7.12.

We draw the weight diagram for the adjoint representation in Figure 8. Note that in this case the dimension of the weight space for the weight $0$ is two. We say the weight has multiplicity two, and indicate this on the weight diagram by circling the weight twice. If the multiplicity was much higher, we would need another method (like writing the multiplicity next to the circle as a number).

Figure 8: Weights for the adjoint representation.