7 SL₃ 7.5 Tensor constructions 7.7 Weyl symmetry — not examinable

7.6 Highest weights

We now develop the theory of highest weights, analogous to that for $\mathfrak{sl}_{2,\mathbb{C}}$ . We first carry out the fundamental weight calculation (the analogue of Lemma 6.10).

Lemma 7.18.

(Fundamental Weight Calculation). Let $V$ be a representation of $\mathfrak{sl}_{3,\mathbb{C}}$ and let $v\in V_{\beta}$ be a weight vector with weight $\beta\in\mathfrak{h}^{*}$ . Let $\alpha\in\mathfrak{h}^{*}$ be a root and let $X_{\alpha}\in\mathfrak{g}_{\alpha}$ be a root vector. Then

X_{\alpha}(v)\in V_{\alpha+\beta}.

Thus we obtain a map

X_{\alpha}:V_{\beta}\longrightarrow V_{\alpha+\beta}.

Proof.

Let $H\in\mathfrak{h}$ . Then

H(X(v))=([H,X]+XH)(v)=\alpha(H)X(v)+X(\beta(H)v)=(\alpha+\beta)(H)X(v).\qed

Example 7.19.

We work this out for the adjoint representation. Recall that, for $i\neq j$ , we have the root $\alpha_{ij}=L_{i}-L_{j}$ with root vector $E_{ij}$ . The above calculation shows that, if $\alpha$ and $\beta$ are roots, then $[\mathfrak{g}_{\alpha},\mathfrak{g}_{\beta}]\subset\mathfrak{g}_{\alpha+\beta}$ . Here are some examples:

•

If $\alpha=\alpha_{12}$ , $\beta=\alpha_{13}$ , then $\alpha+\beta$ is not a root so $\mathfrak{g}_{\alpha+\beta}=0$ . Thus $[E_{12},E_{23}]=0$ (which could also be checked directly).
•

If $\alpha=-\beta$ then we get

$[\mathfrak{g}_{\alpha},\mathfrak{g}_{-\alpha}]\subset\mathfrak{g}_{0}=% \mathfrak{h}.$
•

If $\alpha=\alpha_{12}$ , $\beta=\alpha_{23}$ , then $\alpha+\beta=\alpha_{13}$ and we get

$[E_{12},E_{23}]\in\mathfrak{g}_{\alpha_{13}}=\left\langle E_{13}\right\rangle.$

In fact, you can check that $[E_{12},E_{23}]=E_{13}$ .

Exercise 7.20.

Let $V$ be a finite-dimensional irreducible representation of $\mathfrak{sl}_{3,\mathbb{C}}$ . Then the weights occurring in $V$ all differ by integral linear combinations of the roots of $\mathfrak{sl}_{3,\mathbb{C}}$ , that is, by integral linear combinations of $L_{i}-L_{j}$ .

With regard to the weight diagram, we observe that the ’positive’ root vectors $E_{12}$ , $E_{23}$ , $E_{13}$ move in the ’northeast’ direction while the ’negative’ root vectors move in the ’southwest’ direction (roughly speaking). See Figure 9.

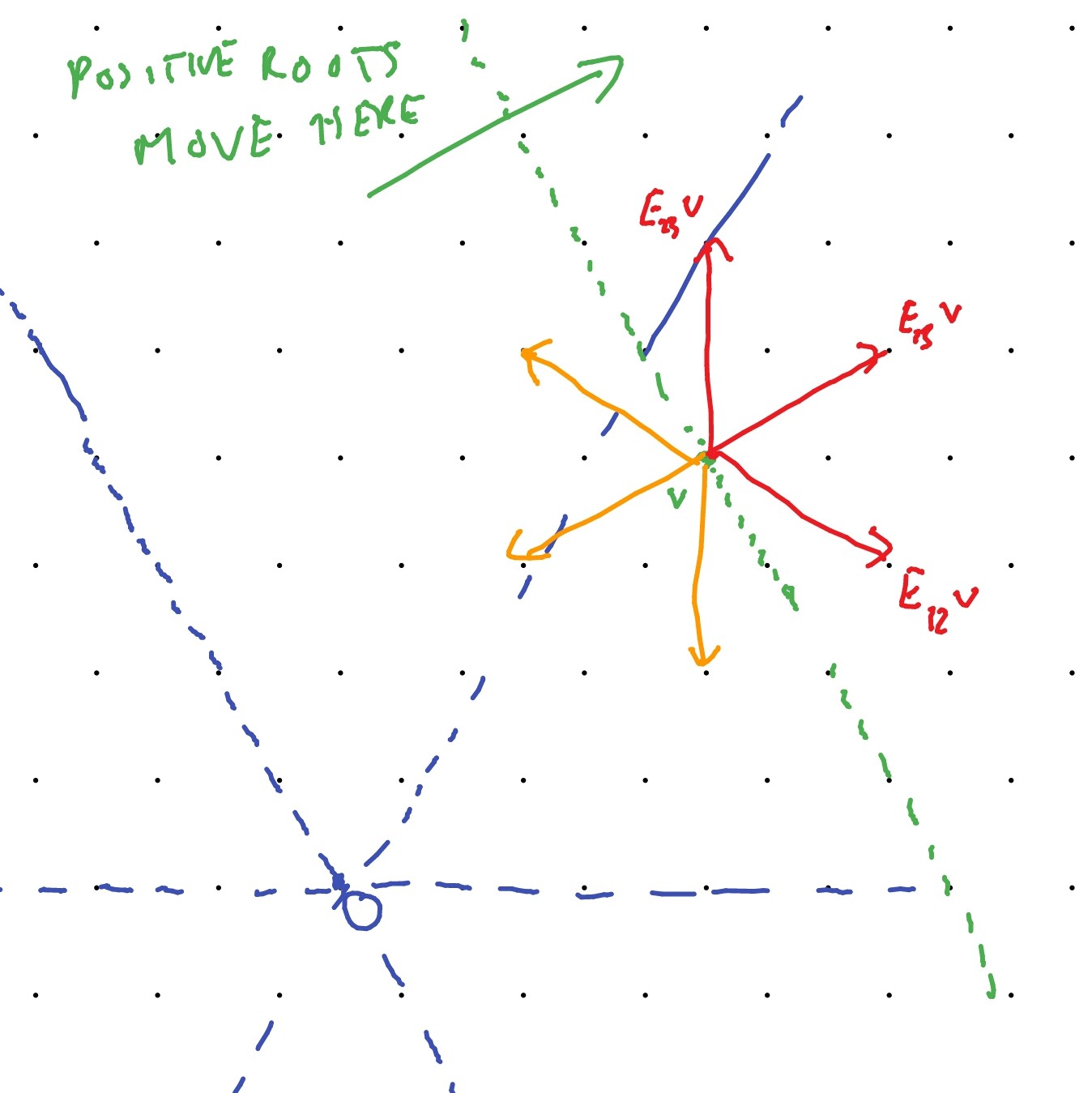
Definition 7.21.

Let $(\rho,V)$ be a representation of $\mathfrak{sl}_{3,\mathbb{C}}$ . A highest weight vector in $V$ is a vector $v\in V$ such that:

1.

$v$ is a weight vector; and
2.

$\rho(E_{12})v=\rho(E_{23})v=0$ .

The weight of $v$ is then a highest weight for $V$ .

Remark 7.22.

Since $[E_{12},E_{23}]=E_{13}$ , it follows that a highest weight vector is also killed by $E_{13}$ . So it is killed by all the positive root vectors.

Example 7.23.

1.

The standard representation $V$ has highest weight $L_{1}$ with highest weight vector $e_{1}$ .
2.

The dual $V^{*}$ has highest weight $-L_{3}$ with highest weight vector $e_{3}^{*}$ .
3.

The adjoint representation has highest weight $L_{1}-L_{3}$ with highest weight vector $E_{13}$ .
4.

The symmetric square $\operatorname{Sym}^{2}(\mathbb{C}^{3})$ has highest weight $2L_{1}$ with highest weight vector $e_{1}^{2}$ .

Lemma 7.24.

Let $V$ be a finite-dimensional representation of $\mathfrak{sl}_{3,\mathbb{C}}$ . Then $V$ has a highest weight vector.

Proof.

For a weight $\alpha=\alpha_{1}L_{1}+\alpha_{1}L_{2}+\alpha_{3}L_{3}$ , define $l(\alpha)=\alpha_{1}-\alpha_{3}$ . Of all the finitely many weights of $V$ , choose a weight $\alpha$ such that $l(\alpha)$ is maximal.

Let $v$ be a weight vector with this weight. Then $E_{12}v$ , if nonzero, has weight

\alpha+L_{1}-L_{2}

and

l(\alpha+L_{1}-L_{2})=l(\alpha)+l(L_{1}-L_{2})=l(\alpha)+1>l(\alpha).

This is not a weight of $V$ by maximality of $l(\alpha)$ . Thus $E_{12}v=0$ . Similarly $E_{23}v$ , if nonzero, has weight

\alpha+L_{2}-L_{3}

and $l(\alpha+L_{2}-L_{3})=l(\alpha)+1$ , so $E_{23}v=0$ . ∎