2 Character theory 2.4 Inner products and homomorphisms 2.6 Linear algebra constructions

2.5 Universal projections

The map $\pi$ constructed in step 1 of the proof of Theorem 2.28 has an interesting feature: for every representation $V$ , the map $\pi$ is a $G$ -homomorphism $V\rightarrow V^{G}$ . We can generalise this substantially.

Let $\alpha:G\rightarrow\mathbb{C}$ be any class function. Then define

\pi_{\alpha}=\frac{1}{|G|}\sum_{g\in G}\overline{\alpha}(g)[g]\in\mathbb{C}[G].

For every representation $(\rho,V)$ , $\pi_{\alpha}$ acts on $V$ , and we also call this $\pi_{\alpha}$ :

\pi_{\alpha}(v)=\frac{1}{|G|}\sum_{g\in G}\overline{\alpha}(g)\rho(g).

If we take $\alpha$ to be the constant function with value 1, then $\pi_{\alpha}$ is the projection $\pi:V\rightarrow V^{G}$ .

Lemma 2.30.

If $V$ is any representation, then $\pi_{\alpha}:V\rightarrow V$ is a $G$ -homomorphism.

Proof.

Let $g\in G$ . Then we have

	$\displaystyle\pi_{\alpha}(\rho(g)v)$	$\displaystyle=\frac{1}{\|G\|}\sum_{h\in G}\overline{\alpha}(h)\rho(h)\rho(g)v$
		$\displaystyle=\rho(g)\frac{1}{\|G\|}\sum_{h\in G}\overline{\alpha}(h)\rho(g^{-1}% hg)v$
		$\displaystyle=\rho(g)\frac{1}{\|G\|}\sum_{h\in G}\overline{\alpha}(g^{-1}hg)\rho% (g^{-1}hg)v$
as $\alpha$ is a class function
		$\displaystyle=\rho(g)\pi_{\alpha}(v)$
replacing $h$ by $g^{-1}hg$ . ∎

Since $\pi_{\alpha}$ is a $G$ -homomorphism $V\rightarrow V$ for every $V$ , we could call it a universal $G$ -homomorphism.

What happens when we take $V$ to be an irreducible representation?

Proposition 2.31.

Let $\alpha$ be a class function and let $V$ be an irreducible representation with character $\chi$ . Then $\pi_{\alpha}$ acts as the scalar

\frac{1}{\dim(V)}\left\langle\alpha,\chi\right\rangle

on $V$ .

In particular, if $\psi$ is the character of an irreducible representation $W$ , then $\pi_{\psi}$ acts as $\frac{1}{\dim W}$ on $W$ and as 0 on all other irreducible representations.

Proof.

If $V$ is irreducible, then by Schur’s lemma $\pi_{\alpha}\in\operatorname{Hom}_{G}(V,V)$ must be a scalar. But its trace is

\operatorname{tr}\pi_{\alpha}=\frac{1}{|G|}\sum_{g\in G}\overline{\alpha}(g)% \chi(g)=\left\langle\alpha,\chi\right\rangle.

Since the trace of a scalar matrix is just the dimension times that scalar, we get the proposition. ∎

Recall now that, if $\rho$ is an irreducible representation of $G$ and $V$ is another representation of $G$ , then $V(\rho)$ denotes the subrepresentation of $V$ generated by all the subrepresentations of $V$ isomorphic to $\rho$ .

Corollary 2.32.

Let $\rho$ be an irreducible representation of $G$ with character $\chi$ and dimension $d$ . Then the operator $d\pi_{\psi}$ acts, on any $G$ -representation $V$ , as the $G$ -equivariant projection

V\rightarrow V(\rho).

Proof.

We have $V\cong\bigoplus_{\sigma\in\mathrm{Irr}(G)}V(\sigma)$ by Maschke’s Theorem. By the proposition, $d\pi_{\psi}$ kills $V(\sigma)$ for $\sigma\not\cong\rho$ , and acts as the identity on $V(\rho)$ , as required. ∎

So $\dim(\rho)\pi_{\psi}$ projects any representation $V$ onto its $\rho$ -isotypic component. In particular, if $V$ has a unique subrepresentation isomorphic to $\rho$ , then $\dim(\rho)\pi_{\psi}$ is a projection onto that subrepresentation.

Corollary 2.33.

The irreducible characters are a basis for the space of class functions.

Proof.

We already know that they are linearly independent (since they are mutually orthogonal vectors in a Hermitian inner product space), so we have to show that they span. Let $C$ be the space of class functions, and let $X$ be the subspace spanned by the irreducible characters. Then $C=X\oplus X^{\perp}$ , and we must show $X^{\perp}=0$ . Suppose that $\alpha\in X^{\perp}$ , so $\left\langle\chi,\alpha\right\rangle=0$ for every irreducible character $\chi$ .

We consider the operator $\pi_{\alpha}=\frac{1}{|G|}\sum_{g\in G}\overline{\alpha}(g)[g]$ . This acts as (a multiple of)

\left\langle\alpha,\chi\right\rangle=\left\langle\chi,\alpha\right\rangle=0

on every irreducible representation $V$ with character $\chi$ . As every representation is a direct sum of irreducibles, we see that $\pi_{\alpha}$ acts as zero on all representations of $V$ .

However, considering the action of $\pi_{\alpha}$ on the regular representation $\mathbb{C}[G]$ , we see that

\pi_{\alpha}([e])=\frac{1}{|G|}\sum_{g\in G}\overline{\alpha}(g)[g].

Since this must be zero, we have $\alpha(g)=0$ for all $g\in G$ , as required. ∎

Corollary 2.34.

Parts (2) and (3) of Theorem 2.17 are true.

Proof.

Part (2) follows from the obvious fact that the dimension of the space of class functions is the number of conjugacy classes, together with Corollary 2.33.

For part (3), consider the matrix obtained by multiplying each entry of the character table by $\sqrt{|\mathcal{C}_{i}|/|G|}$ , where $\mathcal{C}_{i}$ is the conjugacy class labeling the column. Then row orthogonality says that this is a (square) unitary matrix. But the transpose of a unitary matrix is unitary, which gives the column orthogonality. ∎

Example 2.35.

We give an example of how to use the projection operators. Let $G=S_{4}$ , and let $(\sigma,V)$ be the permutation representation on the set of eight vertices of the cube. Its character $\theta$ is given below.

\begin{array}[h]{c|rrrrr}&e&(12)&(12)(34)&(123)&(1234)\\ &1&6&3&8&6\\ \hline\cr\theta&8&0&0&2&0\\ \chi&3&1&-1&0&-1.\end{array}

Then we compute $\left\langle\theta,\theta\right\rangle=4$ , and (by inspection) that $\chi=\mathbbm{1}\oplus\epsilon\oplus\rho\oplus\rho\epsilon$ where $\rho$ is the standard three-dimensional representation of $S_{4}$ whose character $\chi$ is also shown in the table. We label the vertices as in Figure 2, where the labels are shown in red: the labels on the top face are $1,2,3,4$ running counterclockwise, and the label on the vertex opposite $i$ is $i+4$ , and look for a subspace of $V$ isomorphic to $\rho$ .

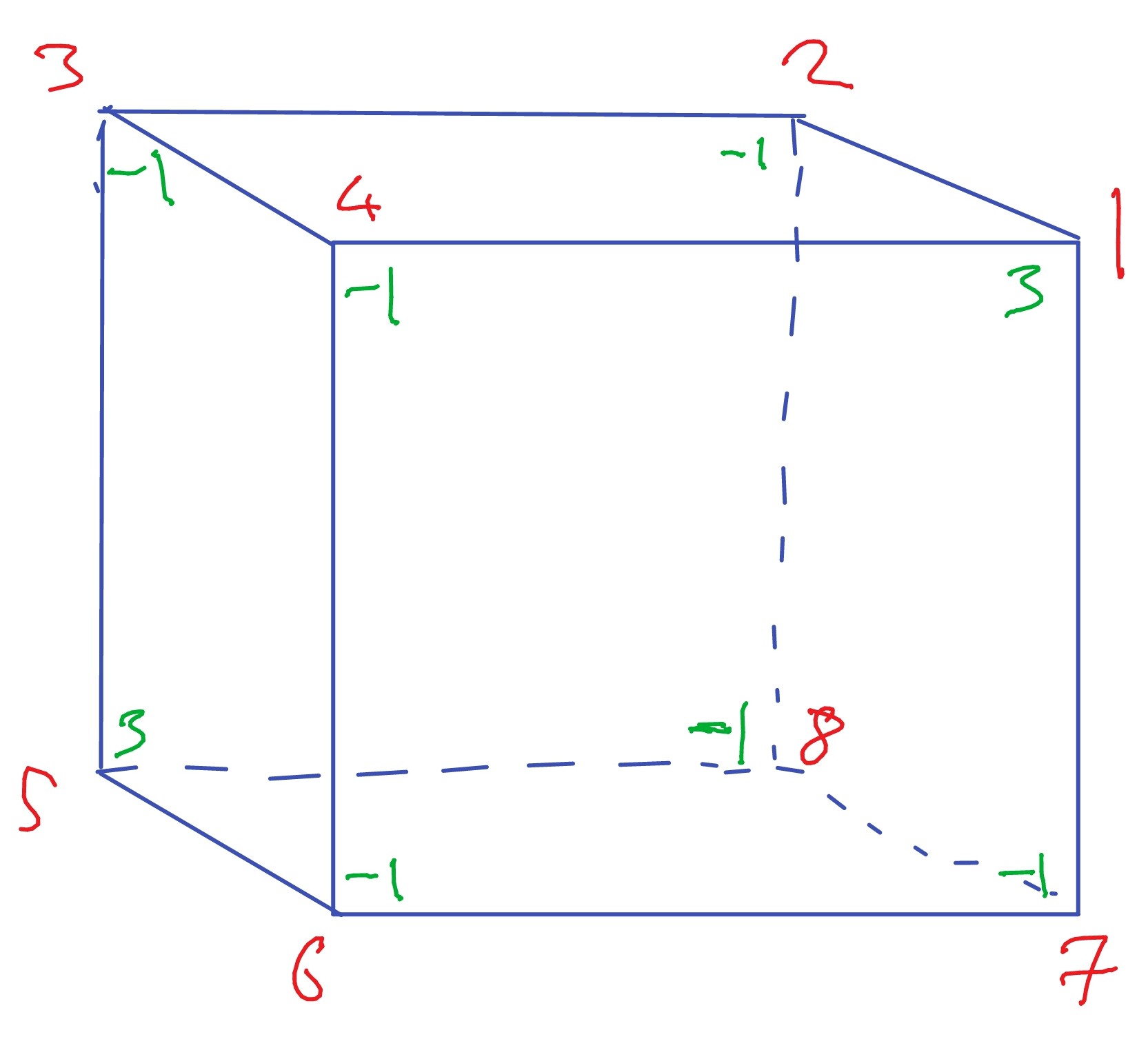
To do this we use the projection operator $\dim(\rho)\pi_{\chi}=\frac{3}{24}\sum_{g\in S_{4}}\overline{\chi}(g)\sigma(g)$ . Applying this to $e_{1}$ , we obtain:

\frac{3}{24}(3e_{1}+e_{2}+e_{4}+e_{7}+3e_{5}-e_{3}-e_{6}-e_{8}-2e_{2}-2e_{4}-2% e_{7})

which simplifies to (writing $f_{i}=e_{i}+e_{i+4}$ )

\frac{1}{8}(3f_{1}-f_{2}-f_{3}-f_{4}).

This is illustrated in green in Figure 2. Starting with a different vector $e_{i}$ will permute the roles of the $f_{i}$ , and we see the the image of $\pi_{\chi}$ is the subspace of $V$ where the coefficients of opposite vertices are equal, and the sum of all the coefficients is zero. This is therefore the subspace of $V$ isomorphic to $\rho$ !

Exercise 2.36.

Complete this example by finding the other irreducible subrepresentations of $V$ .