Assignment 1
Exercise 1.11 At time \(T\) a call option has value \((S_T - K)^{+} = \max\{S_T-K,0\}\), a put option has value \((K-S_T)^{+} = \max\{K-S_T,0\}\) and a share of stock has value \(S_T.\) If we have sold assets (so that we are short in those assets) their value to us will be negative. For example, if we are short one share then its value to us is \(-S_T < 0\), since it will cost us something to buy back the share.
Therefore, the time \(T\) portfolio values are:
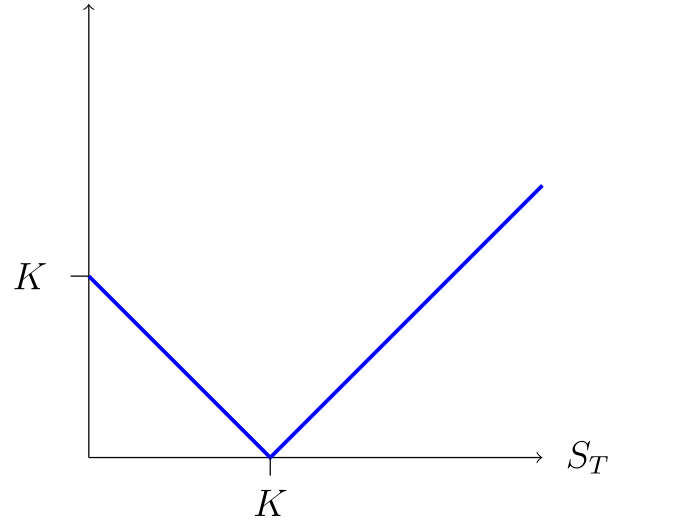
- In the first portfolio, \[(S_T-K)^{+} + (K-S_T)^{+} = \max\{S_T-K,K-S_T\} = |S_T-K| = \begin{cases} K-S_T &\text{if $S_T < K$},\\ S_T-K & \text{if $S_T \geq K$}. \end{cases}\]
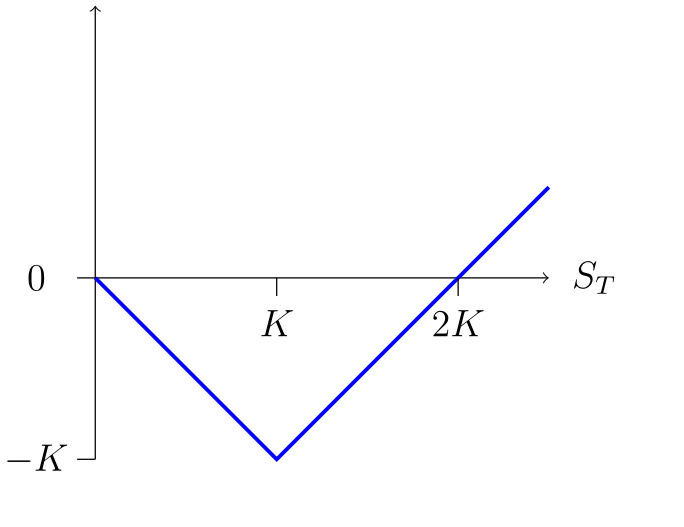
- In the second, \[ 2(S_T-K)^{+} - S_T = \begin{cases} -S_T & \text{if $S_T<K$},\\ S_T-2K & \text{if $S_T \geq K$}. \end{cases}\]
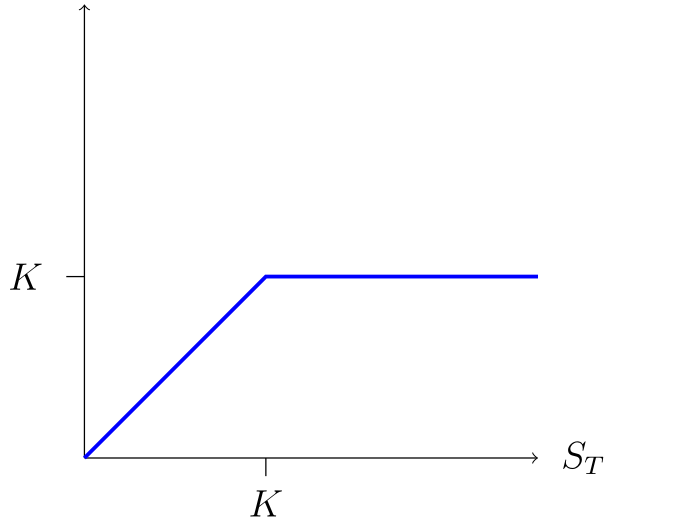
- In the third, \[S_T - (S_T-K)^{+} = \min\{S_T, K\} = \begin{cases} S_T &\text{if $S_T < K$},\\ K & \text{if $S_T \geq K$}. \end{cases}\]
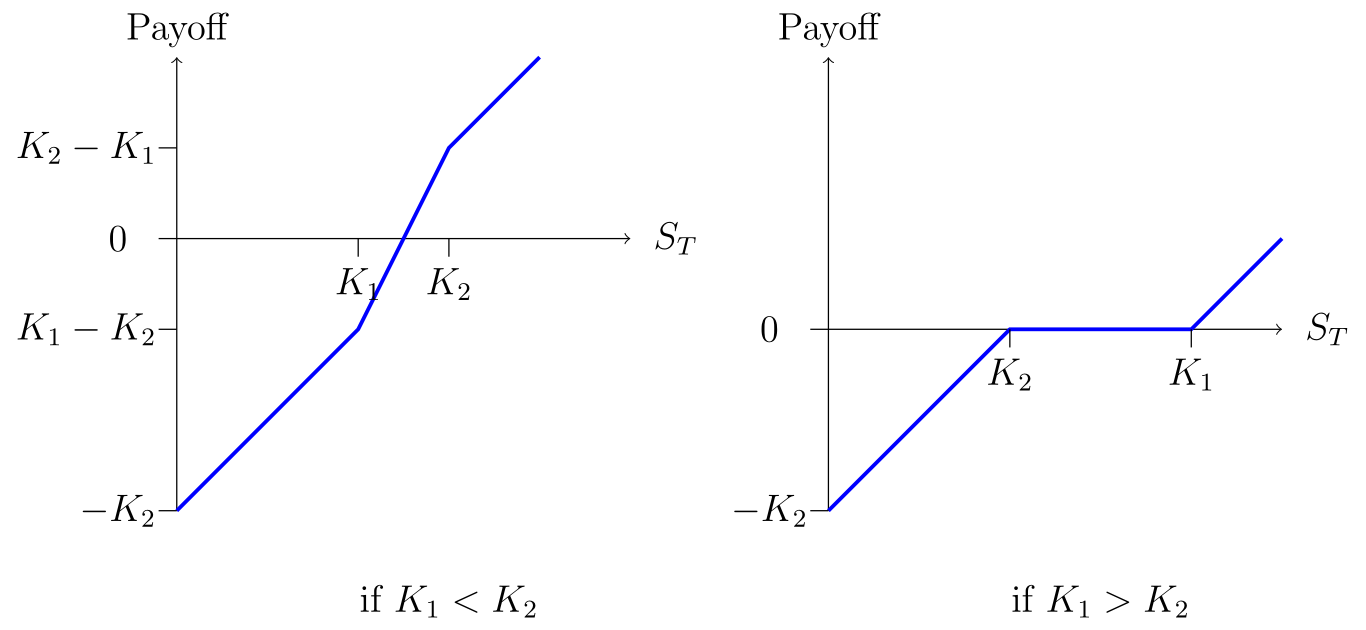
- In the fourth, \[(S_T-K_1)^{+} - (K_2-S_T)^{+} = \begin{cases} S_T-K_2 & \text{if $S_T< \min\{K_1, K_2\}$}, \\ S_T-K_1 & \text{if $S_T> \max\{K_1, K_2\}$}, \\ 2S_T - K_1 - K_2 & \text{if $K_1 \leq S_T \leq K_2$},\\ 0 & \text{if $K_2 \leq S_T \leq K_1$}. \end{cases}\]
Note that typically only one of the last two cases can occur, depending on the values of \(K_1\) and \(K_2.\)
Exercise 1.12 We follow the approach used in Example 1.4, but for an arbitrary time \(t \in (0,T]\), and here interest is compounded continuously.
For all \(t \in (0,T]\), we can just consider what happens over the time interval \([0,t]\) (in other words, since the end point \(T\) is just an arbitrary positive time, we could rename it \(t\)). Then the present value of the profit at time \(t\) of a self-financing portfolio is \(\e^{-rt}V_t - V_0.\)
Consider the portfolio of \(x\) units of the risk-free asset held from time 0 to time \(t\). This is self-financing (there are no trades after time \(0\)), so the present value profit equals \[ \e^{-rt} x B_t - x B_0 = x ( \e^{-rt} B_t - B_0 ) \tag{1.1} \] with certainty. Since \(B_t\) is known to us at time \(0\), we can choose \(x\) strictly positive if \(B_t > \e^{-rt} B_0\) and \(x\) strictly negative if \(B_t < \e^{-rt} B_0\), to ensure that the expression in (1.1) is strictly positive. Hence this portfolio achieves strictly positive profit with certainty (i.e., it is an arbitrage portfolio), unless \(B_t = \e^{rt} B_0\).
If you prefer to work over a fixed time interval \([0,T]\), then for each (fixed) \(t \in (0,T]\) consider the portfolio of \(x\) units bought time 0 and sold at time \(t\). In other words, using \(h_u \in \R\) to denote the amount of the risk-free asset held at (variable) time \(u \in [0,T]\), we have \[ h_u = \begin{cases} x &\text{if $0 \leq u < t$},\\ 0 &\text{if $t \leq u \leq T$}. \end{cases} \] This is not self-financing (because of the trade at time \(t\)), so we need to take care in calculating the present value of the profit at time \(T\). The cash-flow generated by \(h\) is the amount \(-V_0 = -xB_0\) at time 0 and the amount \(V_{t-} - V_{t} = xB_{t}\) at time \(t\); this has present value \[ \e^{0}\cdot(-x B_0) + \e^{-rt} x B_t = x (\e^{-rt} B_t - B_0). \] The final value of \(h\) at time \(T\) is 0 (since the portfolio is empty). Therefore we determine the same expression as in (1.1) for the profit, and we can then continue the argument as above.
Exercise 1.13
The return at time \(T\) from a bull spread using call options is \(\Phi_{\text{BC}}(S_T) = (S_T-K_1)^{+}- (S_T -K_2)^{+}.\) which is always greater than or equal to 0 (because \(K_1 < K_2\)). This means the present value of the return is also greater than or equal to 0, so to avoid arbitrage the price \(C_{\text{BC}}\) at time 0 of the bull spread must be positive and therefore it requires a positive initial investment to purchase it. For this, the investor has the possibility of gaining a greater amount at time \(T.\)
In contrast, a bull spread using put options has return \(\Phi_{\text{BP}}(S_T) = (K_1-S_T)^{+}-(K_2-S_T)^{+}\) which is always less than or equal to 0, so again to avoid arbitrage its price \(C_{\text{BP}}\) at time 0 must be negative, so in this case the investor receives an amount of money at time 0, and for this they have the possibility of losing a greater amount at time \(T.\)
Writing \(C(K)\) and \(P(K)\) for the prices at time 0 of a call and put option with strike price \(K\), we can relate \(C_{\text{BC}} = C(K_1) - C(K_2) \geq 0\) and \(C_{\text{BP}} = P(K_1)-P(K_2) \leq 0\) using put-call parity (assuming continuously compounded interest): \[ \begin{split} C_{\text{BC}} = C(K_1) - C(K_2) &=(P(K_1)+S_0 - K_1\e^{-rT}) - (P(K_2)+S_0-K_2\e^{-rT})\\ &= P(K_1)-P(K_2) +(K_2-K_1)\e^{-rT}\\ &= C_{\text{BP}} + (K_2-K_1)\e^{-rT}. \end{split} \]
We can also get this by considering the difference in the returns: \(\Phi_{\text{BC}}(S_T) - \Phi_{\text{BP}}(S_T) = K_2 -K_1\) always, so to avoid arbitrage the present value of this difference must be the difference in the two prices at time 0. In other words, \(C_{\text{BC}}-C_{\text{BP}} = (K_2-K_1)\e^{-rT}.\)
Exercise 1.14 To say that \(\mathcal{F}\) is a \(\sigma\)-algebra means that \(\mathcal{F}\) is a collection of subsets of \(\Omega\) such that:
- \(\Omega \in \mathcal{F}\).
- If \(A \in \mathcal{F}\) then its complement \(A^\mathrm{c} \in \mathcal{F}\) too.
- If \(A_1, A_2, \ldots \in \mathcal{F}\) then \(\cup_{n=1}^\infty A_n \in \mathcal{F}\) too.