Chapter 3 Questions for Chapter 3
Warm-up
Exercise 3.1 Consider a binomial price tree two periods long with \(S_0 = 100\), \(u = 2\), \(d = 1/2\). Find the price of the call option with expiry 2 and strike price 150 as a function of \(r\), the interest rate per period.
Exercise 3.2 Consider a 3-period binomial model, with \(u=1.5\), \(d=0.7\), \(r=0.1\), and \(S_0 = 100\). What is the Cox–Ross–Rubinstein price at time 0 of a European call option with strike price \(K=90\) and expiry time \(T=3\)? And what is the CRR price of the option at time 1, if the share price at time 1 is \(S_1 = 70\)?
Main problems
Exercise 3.3 Suppose that the stock price \(S_t\) behaviour over two periods is given by the
following tree:
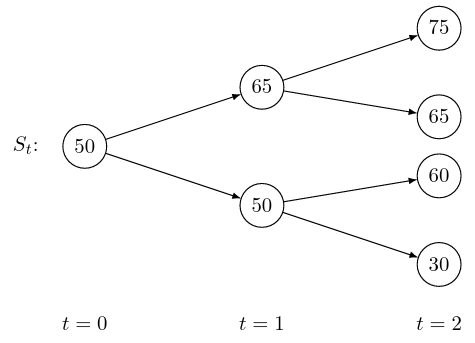and suppose that \(r=0.1\).
Find the martingale probabilities at each node of the tree. Using these probabilities,
find the fair prices of the following digital options:
- a cash-or-nothing call option, with payoff 66 if \(S_2 \geq 50\) and 0 if \(S_2 < 50\),
- an asset-or-nothing call option, with payoff \(S_2\) if \(S_2 \geq 50\) and 0 if \(S_2 < 50\),
Exercise 3.4 On the market defined in the previous question, calculate the no-arbitrage price of a gap option, with payoff \[ \Pi(S_T) = \begin{cases} (S_T - 40) & S_T \geq 65 \\ 0 & S_T < K_t \end{cases}. \]
Exercise 3.5 Suppose that an investor decides to build a self-financing portfolio by investing half of their capital into the risky asset, and the other half into the risk-free asset, at each time step.
Write down a recurrence relation for \(x_{t+1}\) and \(y_{t+1}\) in terms of \(x_{t}\), \(y_{t}\), and \(S_{t+1}\).
Do the same for \(V_{t+1}\), in terms of \(V_{t}\), \(S_{t}\), and \(S_{t+1}\).
Exercise 3.6 Suppose the initial stock price is \(S_0=80\) and that for at each time \(t=1,2,3\) the stock price either increases by 10, or decreases by 10. (So, at time \(t=3\) the stock price can be 50, 70, 90, or 110.) Assume the interest rate is always zero. Can we use the Cox–Ross–Rubinstein formula on this market? What is the fair price of a European call option with strike price 80 and expiry time 3?
Exercise 3.7 Suppose we want to use a multi-period binomial model to model the behaviour of the share price of a risky asset over the course of one year (from \(t=0\) to \(t=1\)). We believe that over this time the most that the share price will increase by is 40% and the most it will decrease by is 20%. We assume that the annual interest rate is 4%, compounded monthly.
What values should we take for \(u, d\) and \(r\) if we wish to model this with a 12-period model, so that the prices change at monthly intervals (\(t=0, 1/12, 2/12, \dots, 1\))?
Is this model arbitrage free?
Supposing the risky asset price at time 0 is 60, what is the price at time 0 of a European put option with strike price 70 and expiry at the end of the year (\(T=1\))?
Exercise 3.8 Find an expression for the price at time \(T-t\) of a European put option with strike price \(K\) and expiry date \(T\), analogous to the Cox–Ross–Rubinstein formula for the price of a call option. Confirm that the CRR prices at time \(T-t\) for a call and put with the same strike price \(K\) and expiry date \(T\) satisfy the put-call parity formula \(P + S_{T-t} = C + K(1+r)^{-t}\).