$$ \def\ab{\boldsymbol{a}} \def\bb{\boldsymbol{b}} \def\cb{\boldsymbol{c}} \def\db{\boldsymbol{d}} \def\eb{\boldsymbol{e}} \def\fb{\boldsymbol{f}} \def\gb{\boldsymbol{g}} \def\hb{\boldsymbol{h}} \def\kb{\boldsymbol{k}} \def\nb{\boldsymbol{n}} \def\tb{\boldsymbol{t}} \def\ub{\boldsymbol{u}} \def\vb{\boldsymbol{v}} \def\xb{\boldsymbol{x}} \def\yb{\boldsymbol{y}} \def\Ab{\boldsymbol{A}} \def\Bb{\boldsymbol{B}} \def\Cb{\boldsymbol{C}} \def\Eb{\boldsymbol{E}} \def\Fb{\boldsymbol{F}} \def\Jb{\boldsymbol{J}} \def\Lb{\boldsymbol{L}} \def\Rb{\boldsymbol{R}} \def\Ub{\boldsymbol{U}} \def\xib{\boldsymbol{\xi}} \def\evx{\boldsymbol{e}_x} \def\evy{\boldsymbol{e}_y} \def\evz{\boldsymbol{e}_z} \def\evr{\boldsymbol{e}_r} \def\evt{\boldsymbol{e}_\theta} \def\evp{\boldsymbol{e}_r} \def\evf{\boldsymbol{e}_\phi} \def\evb{\boldsymbol{e}_\parallel} \def\omb{\boldsymbol{\omega}} \def\dA{\;d\Ab} \def\dS{\;d\boldsymbol{S}} \def\dV{\;dV} \def\dl{\mathrm{d}\boldsymbol{l}} \def\rmd{\mathrm{d}} \def\bfzero{\boldsymbol{0}} \def\Rey{\mathrm{Re}} \def\Real{\mathbb{R}} \def\grad{\boldsymbol\nabla} \newcommand{\dds}[2]{\frac{d{#1}}{d{#2}}} \newcommand{\ddy}[2]{\frac{\partial{#1}}{\partial{#2}}} \newcommand{\pder}[3]{\frac{\partial^{#3}{#1}}{\partial{#2}^{#3}}} \newcommand{\deriv}[3]{\frac{d^{#3}{#1}}{d{#2}^{#3}}} \newcommand{\ddt}[1]{\frac{d{#1}}{dt}} \newcommand{\DDt}[1]{\frac{\mathrm{D}{#1}}{\mathrm{D}t}} \newcommand{\been}{\begin{enumerate}} \newcommand{\enen}{\end{enumerate}}\newcommand{\beit}{\begin{itemize}} \newcommand{\enit}{\end{itemize}} \newcommand{\nibf}[1]{\noindent{\bf#1}} \def\bra{\langle} \def\ket{\rangle} \renewcommand{\S}{{\cal S}} \newcommand{\wo}{w_0} \newcommand{\wid}{\hat{w}} \newcommand{\taus}{\tau_*} \newcommand{\woc}{\wo^{(c)}} \newcommand{\dl}{\mbox{$\Delta L$}} \newcommand{\upd}{\mathrm{d}} \newcommand{\dL}{\mbox{$\Delta L$}} \newcommand{\rs}{\rho_s} $$
1.1 What is a partial differential equation (a PDE)
Let’s write down a famous PDE, the heat/diffusion equation \[ \ddy{u}{t} = D\left(\pder{u}{x}{2} + \pder{u}{y}{2}\right) \] Here we have a scalar function \(u(x,y,t)\), the dependent variable. This function is dependent on two spatial variables, \(x\) and \(y\), and time \(t\). We refer to these as the independent variables. The equation is a balance between various partial derivatives of this function.
A solution to this equation in the above video shows the density \(u\) spreading out. It can be used to model heat diffusing in a room or chemical populations diffusing in solution. The parameter \(D\) is referred to as the diffusion coefficient and represents the rate of spreading (though this is not immediately obvious here).
Let’s be more formal as to what we mean by a PDE:
Definition 1.4 A partial differential equation is an equation containing an unknown function of two or more variables and its partial derivatives with respect to these variables.
We categorise PDE’s by their highest derivative
Definition 1.3 The order of a partial differential equation is the order of its highest-order derivative(s).
They are much easier to tackle if they are linear:
Definition 1.2 A partial differential equation is linear/non-linear if it is respectively linear/non-linear in the dependent variable.
For example, consider the following equations:
\[\begin{align} (a) & \ddy{u}{t} + \pder{u}{x}{3} - 6u\ddy{u}{x} = 0,\\ (b) & \pder{u}{t}{2} + \sin(u)\frac{\partial^2{u}}{\partial x \partial y} =0,\\ (c) & \pder{u}{t}{3} + \sin(x)\frac{\partial^2{u}}{\partial x \partial y}=0. \end{align}\]
Equation (a) is also a famous equation, it is called the Korteweg-DeVries equation. It can be used to model shallow water waves. An example solution is shown below in which a larger faster wave passes through a smaller slower one without them merging
1.2 Solutions to partial differential equations
We have now seen two nice “solutions” to some famous PDE’s. But what do we mean precisely by the term solution?
Definition 1.1 A solution of a PDE in some region \(R\) of the space of the independent variables is a function that possesses all of the partial derivatives that are present in the PDE, in some region containing R, and also satisfies the PDE everywhere in \(R\).
Lets unpack this with an example. Consider again the heat equation: \[ \ddy{u}{t} = D\left(\pder{u}{x}{2} + \pder{u}{y}{2}\right) \] This equation is in two independent spatial variables \(x,y\), so the spatial region \(R\) in our definition should be two dimensional. It should also be true for all time \(t\in(0,\infty]\). Lets assume it is a rectangle of lengths \(Lx,L_y\), so that \(x\in[0,L_x]\) and \(y\in[0,L_y]\) and \(R = [0,L_x]\times[0,L_y]\times(0,\infty]\). Then a solution to the heat equation is
\[ u(x,y,t) = \mathrm{e}^{-D\left(\frac{n^2}{L_x^2} + \frac{m^2}{L_y^2}\right)\pi^2 t}\cos\left(\frac{n\pi x}{L_x}\right)\cos\left(\frac{m\pi y}{L_y}\right), \tag{1.1}\] for some arbitrary integers \((n,m)\). But also so is \[ u(x,y,t) = \mathrm{e}^{-D\left(\frac{n^2}{L_x^2} + \frac{m^2}{L_y^2}\right)\pi^2 t}\sin\left(\frac{n\pi x}{L_x}\right)\sin\left(\frac{m\pi y}{L_y}\right). \tag{1.2}\]
We refer to this as a two-dimensional problem despite \(R = [0,L_x]\times[0,L_y]\times(0,\infty]\) being three dimensional. It is standard practice to refer to the spatial dimension of the domain: this problem is 2D means \(x,y\), and \(t\).
Confirm this by differentiating both solutions and substituting them into the equation.
Since both sides of the equation are equal the equation is satisfied on \(R\). Clearly the derivatives exist everywhere in the domain so it satisfies our definition. But are both valid?
This solution did not appear by magic! It was derived using separation of variables. This was topic 3.3 of Calculus I and problem 2 of the PDF notes was the one-dimensional version of this equation. Problem 3 was the three dimensional version, the 2-d solution method is basically identical. There is an example in your revision quiz but we will also shortly revisit it to go deeper…..
1.2.1 Boundary conditions matter
To fully solve a PDE we must specify boundary conditions. The validity of the solutions Equation 1.2 and Equation 1.1 depend on the boundary conditions used. In this case we must make some statement on what values \(u\) takes on the edges \(x=0,L_x\) and \(y=0,L_y\). We consider two cases:
\[\begin{align} (a)\, & u(0,y,t) = u(L_x,y,t) = u(x,0,t) = u(x,L_y,t)=0.\\ (b)\, & \ddy{u}{x}(0,y,t) = \ddy{u}{x}(L_x,y,t) = \ddy{u}{y}(x,0,t) = \ddy{u}{y}(x,L_y,t)=0. \end{align}\]
We see that, since \(\sin(0) = \sin(n\pi) = 0\), Equation 1.2 satisfies the Dirchlet boundary conditions (a). However, as \(\cos(0)=1\neq 0\) the solution Equation 1.1 does not.
By differentiating the solutions, confirm that Equation 1.2 cannot satisfy boundary conditions (b) and that Equation 1.1 can.
The first set of boundary conditions (a) are an example of Dirichlet boundary conditions, conditions placed on the value of the function on the boundary. The second, (b) are often called Neumann boundary conditions, conditions placed on the derivatives of the function on the boundary. In this case they are homogenous as they are all set equal to zero. If they are not equal to zero they are inhomogeneous. This distinction will come to matter a lot later in the course.
Solutions to partial differential equations (and indeed ordinary differential equations) are not fully defined without their boundary conditions. Later in the course we will see the properties of a differential equation can differ significantly with different boundary conditions and we consider the equation and boundary conditions as one object.
We have seen that boundary conditions can change the solution’s nature. In this case the only obvious change is that there is a non-zero spatially uniform behaviour \(n=m=0\) in the cosine case (no \(x\) or \(y\) dependence), which must be zero in the case of the sin solutions. You will see later this can have significant effects on the behaviour of the system. Throughout this course, when we discuss more general results about differential equations (operators as we shall come to call them), one must always consider the solution and boundary conditions as a single definition.
1.3 Linear equations and the principle of superposition applied to the Heat equation.
A fundamental property of linear PDE’s is that we can add solutions and they will still solve the equation. For example, with Neumann boundary conditions (b) the heat equation has cosine solutions (Equation 1.1) which depended on the choice of arbitrary integers \(n\) and \(m\). We can sum over all the possible values of \(n\) and \(m\) as follows:
\[ u(x,y,t) = \sum_{n=0}^{\infty}\sum_{m=0}^{\infty}C_{nm}\mathrm{e}^{-D\left(\frac{n^2\pi^2 }{L_x^2} +\frac{m^2\pi^2 }{L_y^2} \right)t}\cos\left(\frac{n\pi x}{L_x}\right)\cos\left(\frac{m\pi y}{L_y}\right) \] To see that it is a also a solution to: \[ \ddy{u}{t} = D\left(\pder{u}{x}{2} + \pder{u}{y}{2}\right) \] we differentiate:
\[\begin{align} \pder{u}{x}{2} &= -\frac{n^2\pi^2}{L_x^2}\sum_{n=0}^{\infty}\sum_{m=0}^{\infty}C_{nm}\mathrm{e}^{-D\left(\frac{n^2\pi^2 }{L_x^2} +\frac{m^2\pi^2 }{L_y^2} \right)t}\cos\left(\frac{n\pi x}{L_x}\right)\cos\left(\frac{m\pi y}{L_y}\right) = -\frac{n^2\pi^2}{L_x^2}u,\\ \pder{u}{y}{2} &= -\frac{m^2\pi^2}{L_y^2}\sum_{n=0}^{\infty}\sum_{m=0}^{\infty}C_{nm}\mathrm{e}^{-D\left(\frac{n^2\pi^2 }{L_x^2} +\frac{m^2\pi^2 }{L_y^2} \right)t}\cos\left(\frac{n\pi x}{L_x}\right)\cos\left(\frac{m\pi y}{L_y}\right) = -\frac{m^2\pi^2}{L_y^2}u,\\ \ddy{u}{t} &= -D\left(\frac{n^2\pi^2 }{L_x^2} +\frac{m^2\pi^2 }{L_y^2} \right)\sum_{n=0}^{\infty}\sum_{m=0}^{\infty}C_{nm}\mathrm{e}^{-D\left(\frac{n^2\pi^2 }{L_x^2} +\frac{m^2\pi^2 }{L_y^2} \right)t}\cos\left(\frac{n\pi x}{L_x}\right)\cos\left(\frac{m\pi y}{L_y}\right)\\ &=-D\left(\frac{n^2\pi^2 }{L_x^2} +\frac{m^2\pi^2 }{L_y^2} \right)u. \end{align}\]
Inserting this into the heat equation gives: \[ \ddy{u}{t} = D\left(\pder{u}{x}{2} + \pder{u}{y}{2}\right) \Rightarrow -D\left(\frac{n^2\pi^2 }{L_x^2} +\frac{m^2\pi^2 }{L_y^2} \right)u = -D\left(\frac{n^2\pi^2 }{L_x^2} +\frac{m^2\pi^2 }{L_y^2} \right)u \]
We don’t need to consider negative \(n,m\) due to the symmetry of the sin and cos functions and the fact we have free constants \(C_n\).
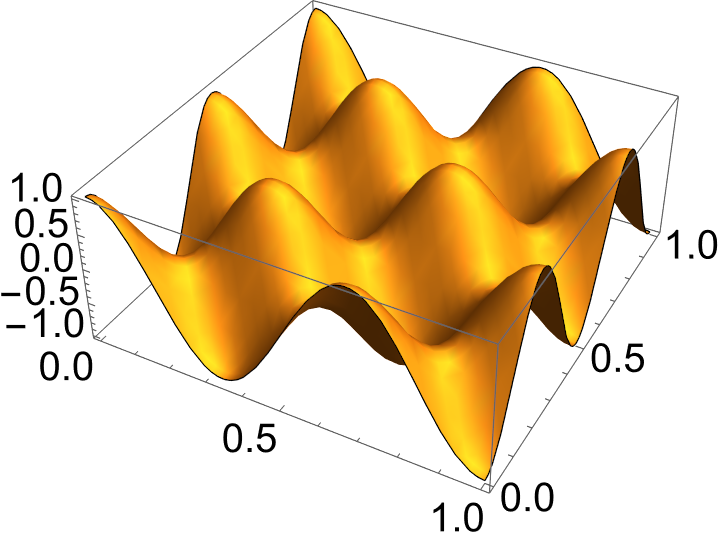
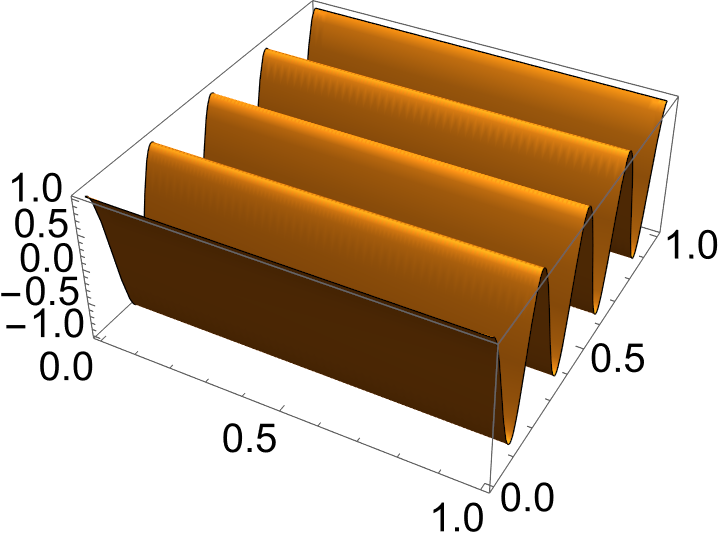
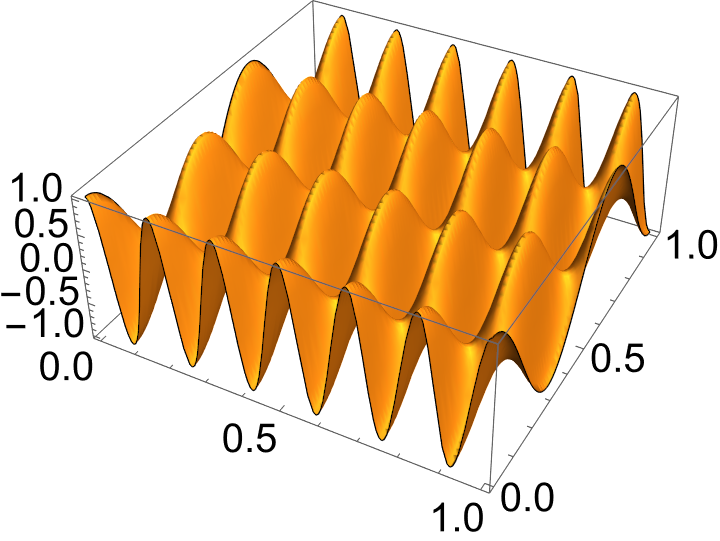
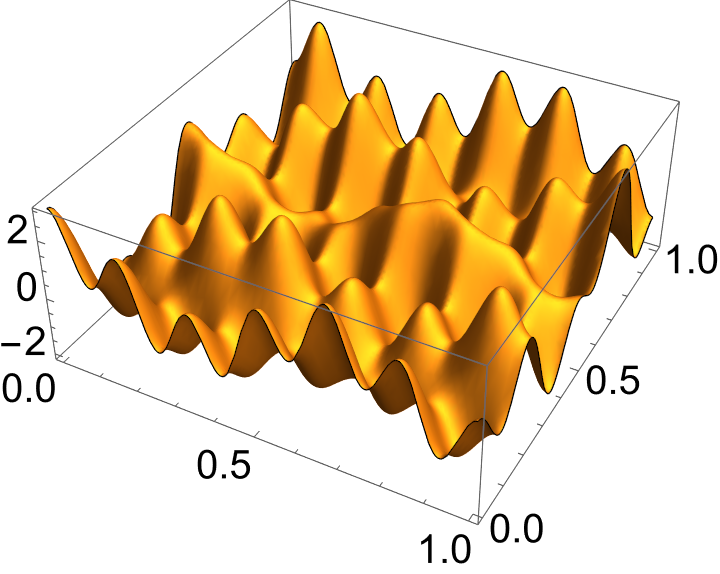
There are a number of points to raise about this sum which we shall repeatedly come back to over the term:
- At \(t=0\) this is just a Fourier series (Chapter 4 in the second term of calculus I). We know these series can represent all the functions we are likely to encounter in this course (more on this later). So the solution can have almost any form initially (at \(t=0\)).
- The terms of a Fourier series are linearly independent: it can only be zero if all terms are individually zero (all \(C_n=0\)). Each “mode” of the system (each component of the sum for \((n,m)\)) has distinct behaviour independent of the others.
The first point means we should expect lots of possible complexity in PDE’s (even a linear one like this)! The second means we can break that complex behaviour down (in the linear case) into the behaviour of simple functions, cosines in this case.
This is an example of the superposition principle, it is visually illustrated in Figure 1.1 where we see three regular modes superimposed to produce a complex and irregular function.
This second observation is fundamental to the mathematics we will explore in this course:
In order to explore important mathematical properties and questions surrounding the superposition principle, we should first remind ourselves of some key Calculus 1 material which I need you to “recall”:
1.4 Fourier series: a recap .
1.4.1 🔁 Recap: General Fourier series on \([0,L]\)
Any suitably smooth function \(f(x)\) defined on \([0,L]\) can be expanded as a full Fourier series \[ f(x)=\frac{a_0}{2} +\sum_{n=1}^{\infty}\left[ a_n\cos\!\Big(\frac{n\pi x}{L}\Big) +b_n\sin\!\Big(\frac{n\pi x}{L}\Big) \right]. \]
The coefficients are \[ a_0=\frac{2}{L}\int_0^L f(x)\,dx,\, a_n=\frac{2}{L}\int_0^L f(x)\cos\!\Big(\frac{n\pi x}{L}\Big)\,dx,\, b_n=\frac{2}{L}\int_0^L f(x)\sin\!\Big(\frac{n\pi x}{L}\Big)\,dx. \]
This form makes no symmetry assumptions about \(f(x)\).
If the function is even or odd, only the cosine or sine terms respectively remain, but the general form above covers both cases automatically.
1.4.2 🔁 Recap: Complete 2D Fourier series on \([0,L_x]\times[0,L_y]\)
\[ \begin{aligned} f(x,y)= &\sum_{m=0}^{\infty}\sum_{n=0}^{\infty}\Big[ a_{mn}\cos\!\Big(\frac{m\pi x}{L_x}\Big)\cos\!\Big(\frac{n\pi y}{L_y}\Big) + b_{mn}\cos\!\Big(\frac{m\pi x}{L_x}\Big)\sin\!\Big(\frac{n\pi y}{L_y}\Big) \\ &\qquad\qquad\qquad\qquad + c_{mn}\sin\!\Big(\frac{m\pi x}{L_x}\Big)\cos\!\Big(\frac{n\pi y}{L_y}\Big) + d_{mn}\sin\!\Big(\frac{m\pi x}{L_x}\Big)\sin\!\Big(\frac{n\pi y}{L_y}\Big)\Big]. \end{aligned} \] Coefficients (uniform half-rectangle formulas): \[ \begin{aligned} a_{00}&=\frac{4}{L_xL_y}\!\int_{0}^{L_x}\!\!\int_{0}^{L_y} f\,dy\,dx,\\ a_{mn}&=\frac{4}{L_xL_y}\!\int_{0}^{L_x}\!\!\int_{0}^{L_y} f\cos\!\Big(\frac{m\pi x}{L_x}\Big)\cos\!\Big(\frac{n\pi y}{L_y}\Big)\,dy\,dx,\\ b_{mn}&=\frac{4}{L_xL_y}\!\int_{0}^{L_x}\!\!\int_{0}^{L_y} f\cos\!\Big(\frac{m\pi x}{L_x}\Big)\sin\!\Big(\frac{n\pi y}{L_y}\Big)\,dy\,dx,\\ c_{mn}&=\frac{4}{L_xL_y}\!\int_{0}^{L_x}\!\!\int_{0}^{L_y} f\sin\!\Big(\frac{m\pi x}{L_x}\Big)\cos\!\Big(\frac{n\pi y}{L_y}\Big)\,dy\,dx,\\ d_{mn}&=\frac{4}{L_xL_y}\!\int_{0}^{L_x}\!\!\int_{0}^{L_y} f\sin\!\Big(\frac{m\pi x}{L_x}\Big)\sin\!\Big(\frac{n\pi y}{L_y}\Big)\,dy\,dx. \end{aligned} \] Here we make it clear the \(a_{00}\) component is the mean value of \(f(x)\), also note some coefficients will be zero as \(\sin(0)=0\) (a minor cost of a compact formula).
Orthogonality and uniqueness of Fourier coefficients
These coefficient formulas reply on the fact trigonometric functions used in a Fourier series are orthogonal over an arbitrary finite interval \([a,b]\) (and hence \([0,L]\)).
Specifically, for integers \(m \neq n\), \[
\int_a^b
\cos\!\left(\frac{n\pi(x-a)}{b-a}\right)
\cos\!\left(\frac{m\pi(x-a)}{b-a}\right)\,dx = \delta_{nm},
\] and likewise for the sine terms.
Also \[ \int_a^b \cos\!\left(\frac{n\pi(x-a)}{b-a}\right) \sin\!\left(\frac{m\pi(x-a)}{b-a}\right)\,dx =0, \] for any \(n,m\).
Orthogonality also provides a practical way to isolate each coefficient and leads to the formulae above.
Multiplying both sides of a Fourier expansion by one of the basis functions and integrating over the domain gives \[\begin{align}
\int_a^b u(x)\cos\!\left(\frac{m\pi(x-a)}{b-a}\right)\,dx
&=\int_a^b\cos\!\left(\frac{m\pi(x-a)}{b-a}\right) \sum_{n=1}^{\infty}\left[
a_n\cos\!\Big(\frac{n\pi x}{L}\Big)
+b_n\sin\!\Big(\frac{n\pi x}{L}\Big)
\right] \\
&= a_m \int_a^b
\cos^2\!\left(\frac{m\pi(x-a)}{b-a}\right)\,dx,
\end{align}\] where we have used the fact orthogonality means all the terms except one vanish. so that \[
a_m =
\frac{
\displaystyle\int_a^b
u(x)\cos\!\left(\frac{m\pi(x-a)}{b-a}\right)\,dx
}{
\displaystyle\int_a^b
\cos^2\!\left(\frac{m\pi(x-a)}{b-a}\right)\,dx
}.
\] This process—multiplying by a mode and integrating—uses orthogonality to extract the amplitude of that mode uniquely from the full function.
It is this property that makes Fourier and other eigenfunction expansions so powerful: they allow complex functions to be decomposed uniquely into independent, orthogonal components, i.e. it means the series: \[
f(x)=\frac{a_0}{2}
+\sum_{n=1}^{\infty}\left[
a_n\cos\!\Big(\frac{n\pi x}{L}\Big)
+b_n\sin\!\Big(\frac{n\pi x}{L}\Big)
\right].
\] (and its 2D counterpart) is linearly independent, only zero if all coefficients \(a_n,b_n\) are identically zero This will matter a lot later.
Try the additional examples in questions 1. and 2. of problem sheet 1.
Try question 3 of problem sheet 1 which covers solutions to the heat equation with periodic boundary conditions, a case for which all Fourier components are active.
I will show you how to use the following colab notebook to calculate and plot your own Fourier series in the lecture. I would encourage you to try it out and get a feel for how accurate the series is if you don’t sum all the way to infinity, that is a crucial practical issue (not examinable in this course)!
[link]
One crucial point we will note playing with this notebook in class is that if you generate Fourier series with random coefficients, they are almost always a mess, nothing like the smooth functions one gets when solving a PDE. In short the PDE is choosing the coefficients very carefully to achieve a specific behaviour
1.5 The Heat equation solution as a Fourier Series.
The critical point regarding the Fourier series is that any reasonable (square integrable) function can be represented by it. There is a vast menu of functions to choose from! All we have to do is choose the coefficients to make a specific function. The Heat equation gives us a rule for choosing them (more accurately how they change over time).
We can see this as follows, write the solution as a Fourier series:
\[ u(x,y,t) = \sum_{n=0}^{\infty}\sum_{m=0}^{\infty}T_{nm}(t)\cos\left(\frac{n\pi x}{L_x}\right)\cos\left(\frac{m\pi y}{L_y}\right), \] (a reminder we are assuming Neumann boundary conditions so only \(\cos()\cos()\) is allowed). If we put this into the heat equation we get: \[\begin{align} \ddy{u}{t} &= \sum_{n=0}^{\infty}\sum_{m=0}^{\infty}\dds{T_{nm}}{t}\cos\left(\frac{n\pi x}{L_x}\right)\cos\left(\frac{m\pi y}{L_y}\right)\\ &= -D\sum_{n=0}^{\infty}\sum_{m=0}^{\infty}\left(\frac{n^2\pi^2}{L_x^2}+\frac{m^2\pi^2}{L_y^2}\right)T_{nm}(t)\cos\left(\frac{n\pi x}{L}\right)\cos\left(\frac{m\pi y}{L}\right) \end{align}\] bring it together: \[ D\sum_{n=0}^{\infty}\sum_{m=0}^{\infty}\left[\dds{T_{nm}}{t}+\left(\frac{n^2\pi^2}{L_x^2}+\frac{m^2\pi^2}{L_y^2}\right)T_{nm}(t)\right]\cos\left(\frac{n\pi x}{L}\right)\cos\left(\frac{m\pi y}{L}\right)=0. \] Now we make a big assumption, that this is only satisfied if each term of the sum is identically zero. This is justified by the linear independence of th Fourier series, which relies crucially on the orthogonality of its modes (cosine and sine). If this is the case then we just have to solve the ordinary differential equation O.D.E.: \[ \dds{T_{nm}}{t}+\left(\frac{n^2\pi^2}{L_x^2}+\frac{m^2\pi^2}{L_y^2}\right)T_{nm}(t) =0 \] which has the exponential solution: \[ T_{nm}(t)= a_{nm}\mathrm{e}^{-D\left(\frac{n^2\pi^2}{L_x^2}+\frac{m^2\pi^2}{L_y^2}\right)t}. \]
💡 Separation of variables: This is the second half of the separation of variables method one can use to solve such equations. You covered this in section 3.3 of Calculus 1. We will shortly re-familiarise ourselves with this method as we need to understand how it works better.
The functions \(T_{nm}(t)\) change the weighting of each component, each mode, of the sum over time. In this case (the heat equation) the higher the mode, i.e. the higher the value of \(n\) and \(m\), the faster the decay over time. We also note there are a set of free constants \(a_{nm}\), i.e. when \(t=0\) we have a proper Fourier series:
\[ u(x,y,0) = \sum_{n=0}^{\infty}\sum_{m=0}^{\infty}a_{nm}\cos\left(\frac{n\pi x}{L}\right)\cos\left(\frac{m\pi y}{L}\right) \] Setting the value of the \(a_{nm}\) determines the function \(u(x,y,0)\) which we generally call the initial condition. We can use our Fourier recipe to get the \(a_{nm}\) as follows. Lets say \(u(x,y,0)=f(x,y)\) where \(f(x,y)\) is some initial distribution, which we must impose to fully solve the problem, then we have \[ a_{00} = \frac{4}{L_xL_y}\int_{0}^{L_x}\int_{0}^{L_y}f(x,y)\,dx\,dy \] and \[ a_{mn}=\frac{4}{L_xL_y}\!\int_{0}^{L_x}\!\!\int_{0}^{L_y} f(x,y)\cos\!\Big(\frac{m\pi x}{L_x}\Big)\cos\!\Big(\frac{n\pi y}{L_y}\Big)\,dy\,dx. \]
The choice of initial condition \(u(x,y,0)=f(x,y)\), and the homogenous Neumann boundary conditions we have assumed: \[ \ddy{u}{x}(0,y,t) = \ddy{u}{x}(L_x,y,t) = \ddy{u}{y}(x,0,t) = \ddy{u}{y}(x,L_y,t)=0. \] fully specifies the solution.
1.5.1 Mode decay/growth.
The functions \[ T_{nm}(t)= a_{nm}\mathrm{e}^{-D\left(\frac{n^2\pi^2}{L_x^2}+\frac{m^2\pi^2}{L_y^2}\right)t}. \] decay to zero as \(t\rightarrow \infty\), except in the case \(n=m=0\). Remembering that the spatial behaviour of the modes (their dependence on \(x\) and \(y\)) takes the form \[\cos\left(\frac{n\pi x}{L}\right)\cos\left(\frac{m\pi y}{L}\right) \] we see that \(n=m=0\) is the constant mode. Thus in the limit \(t\rightarrow 0\) the distribution \(u\) becomes uniform (it doesn’t vary in space): \[ u(x,y,t\rightarrow 0) \rightarrow a_{00} \]
| Figure 1(a). 1D evolution of a heat-equation solution. | Figure 1(b). 2D evolution of a heat-equation solution. |
If we think of \(u\) as representing temperature, this would mean a constant temperature. So in the long time frame, whatever the initial state (the values of \(a_{mn}\)) the distribution/temperature will tend to a constant value. This is what we saw in the first video of the chapter, the Heat equation destroys interesting patterns, or flattens/spreads them out. Another common use of it is drug diffusion, in the long time then a drug diffuses to be equally distributed everywhere in whatever fluid it is in. One can see this in the video above for both 1D and 2D cases.
So does the initial condition matter? In this case at the very least if we set \(u(x,y,0)=f(x,y)\) then the mean component: \[ a_{00} = \frac{4}{L_xL_y}\int_{0}^{L_x}\int_{0}^{L_y}f(x,y)\,dx\,dy, \] determines the state as \(t\rightarrow 0\). We will see for other systems the initial condition will matter a lot more.
There can be mode growth. Consider the following time dependent Fourier series \[ u(x,y,t) = \sum_{n=0}^{\infty}\sum_{m=0}^{\infty}T_{nm}(t)\cos\left(\frac{n\pi x}{L_x}\right)\cos\left(\frac{m\pi y}{L_y}\right), \] where the functions \(T_{nm}(t)\) take the form \[ T_{nm}(t) = -\left(\frac{n^2}{L_x^2} + \frac{m^2}{L_y^2} -a\right)^2+\delta ,\quad a>0,\delta>0. \] For the majority of \(n\) and \(m\) values this function is negative and hence would lead to mode decay. However, for example if \(n^2+m^2=a\) (which is only possible for some combinations of \(L_x\), \(L_y\) and \(a\)) then this function can lead to growth. In this case it is likely only one or a couple of modes \(n\) and \(m\).
Pattern formation In physical/biological models individual modes often have some clear physical meaning. For example many models of stripe and spot patterns on animals and other organisms have the \(\cos\) and \(\sin\) modes we have seen above. If only one mode grows then it will be regular and take the form of spots or stripes. The example I have just discussed (the quadratic growth formula) is a simplified representation of the so called Turing mechanism, named after Alan Turing, in which under some change the system is pushed from a state where all modes decay, to where one grows. The video above is an example of such a model where cos and sin modes are fundamental to the formation of a spotted pattern, which then requires non linearities to stablise (no exponential growth in the long run).
1.6 Separation of variables and varying mode behaviour
We can find more complex mode behaviour than simple growth or decay. We will look at the example of the wave equation, and in doing so remind ourselves how to solve Liner PDE’s via separation of variables.
Consider the Wave equation on \([0,L_x]\times[0,L_y],\,t>0\) \[ \pder{u}{t}{2} = c^2\,\left(\pder{u}{x}{2}+\pder{u}{y}{2}\right), \] with homogeneous Neumann boundary conditions \[ \ddy{u}{x}(0,y,t) =\ddy{u}{x}( L_x,y,t)= \ddy{u}{x}( x,0,t)=\ddy{u}{y}(x,\pm L_y,t)=0. \]
For Separation of variables we assume the separation anzatz: Seek solution in a product form \[ u(x,y,t)=X(x)\,Y(y)\,T(t). \] i.e. a solution which can be decomposed in terms of functions which capture the variation of each individual independent variable separately (a massive assumption which we will show later can be justified in lots of cases).
The method is systematic:
Step1: Perform the separation Substitute into the PDE and divide by \(XYT\): \[ \frac{T''}{c^2}XY= X''YT+Y''XT\Rightarrow \frac{T''}{c^2\,T}=\frac{X''}{X}+\frac{Y''}{Y}, \] where the dash represents differentiation with respect to the independent variable i.e. \(X' = d X/dx\)
Since the functions \(X,Y,T\) all depend on distinct independent variables, each term can only cancel each other if they are individually equal to set of constants which cancel. This fact is always asserted for separation of variables.
In the case at hand that means we set \[ \frac{X''}{X}= -\lambda_x,\qquad\frac{Y''}{Y}= -\lambda_y,\qquad \frac{T''}{c^2 T}= -\lambda_t, \] and the equation itself requires that: \[ \lambda_t=\lambda_x+\lambda_y. \] Thus we have to solve the following system of ordinary differential equations:
The minus sign is a convention, it will allow us to associate positive values of \(\lambda\) with the relevant solutions.
\[ X''+\lambda_x X=0,\qquad Y''+\lambda_y Y=0,\qquad T''- c^2\lambda_t T,\quad \lambda_t=\lambda_x+\lambda_y, \] with Neumann BC \(X'(0)=X'(L_x)=0\), \(Y'(0)=Y'(\pm L_y)=0\). Note, the function \(T(t)\) would also require two initial conditions, but that is much less important for what we are focusing on.
Reduction to ODE’s The point of separation of variables is to turn a partial differential equation into a set of Ordinary differential equations. Which we can solve.
Step 2: Solve for the spatial modes We start by solving the spatial modes. First: \[ X''+\lambda_x X=0 \] Since this is a constant coefficient O.D.E we seek solutions in the form \(X = A\mathrm{e}^{kx}\) for some constant \(k\). We substitute this in and factor to obtain: \[ k^2 + \lambda_x =0. \] There are three cases
- \(\lambda_x >0\), for which \(k =\pm\mathrm{i}\sqrt{\lambda_x}\) and hence: \[ A\sin(\sqrt{\lambda_x} x) + B\cos(\sqrt{\lambda_x} x). \]
Show this is the case using De Moivre’s theorem \(\mathrm{e}^{\mathrm{i} \mu x}= \cos(\mu x) + \mathrm{i}\sin(\mu x)\) and the fact we would have: \[ X = A_1\mathrm{e}^{i \sqrt{\lambda}_x x}+A_2\mathrm{e}^{-i \sqrt{\lambda}_x x} \] Hint, the constants \(A_1\) and \(A_2\) can be complex, but we want \(A\) and \(B\) to be real.
Neumann BCs give
\[\begin{align} X'(0)&= B\sqrt{\lambda_x}=0,\\ X'(L_x)&= -A\sqrt{\lambda_x}\sin(\sqrt{\lambda_x}L_x)+B\sqrt{\lambda_x}\cos(\sqrt{\lambda_x}L_x)=0. \end{align}\]
You should confirm can only be made true if \(\sqrt{\lambda_x} = n\pi/L_x\) for \(n= 0,1,\dots\) and \(B=0\).
Thus our solutions take the form: \[ X(x) = A\cos\left(\frac{n\pi}{L}x\right),\quad n=0,1,2,\dots \]
Seeking non-triviality We can of course satisfy the boundary conditions with \(A=B=0\), but this is trivial and no of interest. The point is that if we want no trivial solutions then \(\lambda_x\) must take very specific values, which we shall come to call eigenvalues in the next chapter.
- \(\lambda_x <0\), for which \(k =\pm \sqrt{\lambda_x}\) and hence:
\[ X(x) = A\mathrm{e}^{\sqrt{\lambda_x} x} + B\mathrm{e}^{-\sqrt{\lambda_x} x}. \]
Neumann BCs give
\[\begin{align} X'(0)&=A\sqrt{\lambda_x} -B\sqrt{\lambda_x} =0,\\ X'(L_x)&= A\sqrt{\lambda_x}\mathrm{e}^{\sqrt{\lambda_x} L_x} -B\sqrt{\lambda_x} \mathrm{e}^{-\sqrt{\lambda_x} L_x} =0. \end{align}\]
Show that this exponential solution pair cannot satisfy the boundary conditions except trivially \(A=B=0\). Hint: you should be able to reduce the system of boundary equations to an equation in the form: \[ C \mathrm{e}^{D} =0 \] For which only \(C=0\) is a possibility (hence yielding a trivial solution).
- \(\lambda_x =0\), for which: \[ X''=0\Rightarrow X = Ax+B \] I very much hope you can show this can’t satisfy the boundary conditions unless A=0! We can have \(B\neq 0\) which is equivalent to a \(B\cos(n\pi x/L_x)\) mode with \(n=0\)
So all told:
Spatial eigenmodes for the \(X\) variation of \(u\)
We have now shown that the only permissible solution behaviours for the \(X\) functions, which represent the variation of the solution \(u\) in the \(x\) direction, take the form: \[ X(x) = A\cos\left(\frac{n\pi}{L_x}x\right),\quad n=0,1,2,\dots \] This is associated with the following set values of \(\lambda_x\) (eigenvalues): \[ \lambda_x = \frac{n^2\pi^2}{L_x^2} \] We ruled out any possible exponential or linear behaviour as it could not satisfy the boundary conditions.
Next we note that the \(Y\) modes satisfy the exact same equation, thus:
General spatial eigenmodes for variation of \(u\) The only non-trivial (non-zero) spatial eigenmodes of the solution \(u\) are: \[ \Phi_{mn}(x,y)=X_m(x)Y_n(y) =a_{nm}\cos\!\Big(\frac{m\pi x}{L_x}\Big)\cos\!\Big(\frac{n\pi y}{L_y}\Big), \] with combined spatial eigenvalue \[ \lambda_{mn}=\Big(\frac{m\pi}{L_x}\Big)^2+\Big(\frac{n\pi}{L_y}\Big)^2. \]
Try some similar examples in questions 4-6 of problem sheet 1.
Step 3: Temporal modes The spatial modes give us permissible values for \(\lambda_x\) and \(\lambda_y\) (the spatial eigenvalues). We know that \[ \lambda_t = \lambda_x+ \lambda_y = \lambda_{mn}=\Big(\frac{m\pi}{L_x}\Big)^2+\Big(\frac{n\pi}{L_y}\Big)^2. \]
Boundary conditions detemine temporal growth. It will always be the case, for separation of variables, that the temporal eigenvalues \(\lambda_t\) are set by the allowed spatial eigenvalues, in turn, we saw above these were determined by the boundary condtions. This is the first hint as to why I made a big fuss earlier about the importance of boundary conditions.
Now to solve for the \(T_{nm}\). This is the bit we saw above for the heat equation.For each \((m,n)\), the time factor \(T_{mn}\) solves \[ T_{mn}''+c^2\lambda_{mn}\,T_{mn}=0. \] Hence, for \((m,n)\neq(0,0)\), \[ T_{mn}(t)=A_{mn}\cos\!\big(c\omega_{mn}t\big)+B_{mn}\sin\!\big(c\omega_{mn}t\big), \qquad \omega_{mn}=\sqrt{\lambda_{mn}}. \] For the zero spatial mode \((m,n)=(0,0)\) we have \(\lambda_{00}=0\), so \[ T_{00}''=0\ \Rightarrow\ T_{00}(t)=A_{00}+B_{00}\,t. \]
Note that \(c^2\lambda_{nm}\) cannot be negative, so we do not need to consider exponential solutions.
General separated solution (no initial conditions imposed yet) Assembling all modes: \[ \begin{aligned} &u(x,y,t) = \underbrace{A_{00}+B_{00}\,t}_{\text{zero spatial mode}} \\ &\quad + \sum_{\substack{(m,n)\neq(0,0)}} \Big[ A_{mn}\cos\!\big(c\,\omega_{mn} t\big) + B_{mn}\sin\!\big(c\,\omega_{mn} t\big) \Big]\, \cos\!\Big(\frac{m\pi x}{L_x}\Big)\cos\!\Big(\frac{n\pi y}{L_y}\Big),\\ &\omega_{mn}=\sqrt{\Big(\frac{m\pi}{L_x}\Big)^2+\Big(\frac{n\pi}{L_y}\Big)^2}. \end{aligned} \]
It is often the case that we set \(B_{00}=0\). There is no clear mathematical reason but the assumption is physical. This behaviour grows without bound, whilst all other modees are bounded in time. This unbounded growth is usually considered physically unrealistic.
Quesitons 7 and 8 of problem sheet 1 will give you practice in applying the method of separation of variables.
1.6.1 A comparison of the wave equation and the heat equation mode variation.
Note that the temporal bahaviour of the wave equation modes is purley oscillatory, so they never permanently die away in time like they did in the case of the heat equation.
We see what this means in practice in the videos above, on the left are solutions to the heat equation (first order in time), on the right solutions to the wave equation (second order in time), in 1d and 2d. Both start with the same initial conditions. We see on the left the solution gradually simplify as the small scale (larger \(n,m\)) behaviour decays faster leaving the \(n=1\) mode. In the wave equation case the complexity simply oscillates and moves at a finite speed
Parabolic vs Hyeprbolic equations
In calculus I you were introduced to two types of linear PDE: Parabolic and Hyperbolic, which are commonly associated with time-dependent behaviour. The heat equation is parabolic, a common property of these equations is that they tend to simplify the solution from its initial state. The wave equation is a hyperbolic equation, one of whose characteristic properties is that they maintain the initial complexity of the initial conditions.
In fact this classification and property is commonly applied to non-linear PDE’s, although hard to state. If you want to know more make sure you take PDE’s III next year.
1.6.2 A zoology of parabolic and hyperbolic models.
In class we will look at other cool examples of these equation types on visualPDE.
1.7 There are lots of other spatial modes.
The previous section might give one the idea that the Fourier series is the fundamental object of study for linear PDE’s, nothing could be further from the truth. As we will see, the \(\cos()\) and \(\sin()\) functions (modes) of the Fourier series are the modes/patterns/basic elements of the heat Kernel in Cartesian coordinates: \[ \nabla^2 u =\nabla \cdot \nabla u= \pder{u}{x}{2} + \pder{u}{y}{2}. \] However, every different linear PDE has its own set of modes from which its solutions are constructed. In fact the same operator, the Heat kernel \(\nabla^2 u\) has different modes dependent on the domain geometry. Lets look at a classic example:
1.7.1 Bessel functions and the heat equation on the disc.
We consider the heat equation with constant diffusivity \(D>0\) on a disc: \[ \ddy{u}{t} = D \nabla^2 u,\qquad (r,\theta)\in[0,L_r]\times[0,2\pi), \] with boundary conditions \[ u(L_r,\theta,t)=0\quad \text{ and periodicity in }\theta. \] The periodic nature of the \(\theta\) coordinate demands angular periodicity. The first condition is an example of Homogeneous Dirichlet conditions. We use separation of variables and apply the three-step method:
Step 1: Perform the separation We seek separated solutions \(u(r,\theta,t)=R(r)P(\theta)T(t)\). Substituting into \(\partial_t u=D\nabla^2 u\) and dividing by \(RPT\) gives \[ \frac{T'}{D T}=\frac{1}{RP}\nabla^2(RP) \] again we use the argument that the coordinate independence required both the temporal and spatial behaviours must be equal to the same constant: \[ \frac{T'}{D T} = -\lambda = \frac{1}{RP}\nabla^2(RP) \] note the minus sign convention again. So we have to solve two eigen problems: \[ T'(t) +D\lambda T(t) =0,\quad \nabla^2(RP) = -RP\lambda \] The second equation is the spatial problem which we now tackle.
Step 2: Solve for the spatial modes
The Laplacian (heat kernel) of a function \(y(r,\theta)\) takes the following form in polar coordinates: \[ \nabla^2y = \frac{1}{r}\ddy{}{r}\left(r \ddy{y}{r}\right) + \frac{1}{r^2}\pder{y}{\theta}{2}. \]
The Laplacian is \(\nabla^2 u = \nabla\cdot\nabla u\), it would be great revision for the first half of the course to derive the above result. For questions in my half of the course I would give you the coordinate form as I have done here.
The Dirichlet boundary conditions would take the form \(y =0\). In our case \(y(r,\theta) = R(r)P(\theta)\). Substituting this into our eigenequation we find, \[ \frac{1}{r}\ddy{}{r}\left(r \ddy{(RP)}{r}\right) + \frac{1}{r^2}\pder{(RP)}{\theta}{2} + \lambda RP = P\frac{1}{r}\dds{}{r}\left(r \dds{R}{r}\right) + R\frac{1}{r^2}\deriv{P}{\theta}{2} + \lambda RP= 0. \] Note we are just performing the spatial step of separation of variables. Multiplying both sides of this equation by \(r^2/RP\) we have, \[ \frac{r}{R}\ddy{}{r}\left(r \dds{R}{r}\right) + \frac{1}{P}\pder{P}{\theta}{2} + \lambda r^2 = 0 \implies \frac{r}{R}\dds{}{r}\left(r \dds{R}{r}\right) + \lambda r^2 = - \frac{1}{P}\deriv{P}{\theta}{2} = \lambda_{\theta}, \] where we have separated the \(r\) and \(\theta\) functions. Variable independence again means that both sides of this equation are constant, which we set to be equal to \(\lambda_{\theta}\).
\[\begin{align} \frac{1}{Rr}\dds{}{r}\left(r \dds{R}{r}\right) & = \lambda-\frac{\lambda_\theta}{r^2},\\ - \frac{1}{P}\deriv{P}{\theta}{2} = \lambda_\theta, \end{align}\] and the boundary conditions, \[ R(L_r)=0, \quad P(0) = P(2\pi), \quad \dds{P}{\theta}(0) = \dds{P}{\theta}(2\pi). \] The \(P\) conditions arise from the necessarily periodic nature of the function in the \(\theta\) coordinate (we are assuming some regularity).
Reduction to ODE’s (repeat point) The point of separation of variables is to turn a partial differential equation into a set of Ordinary differential equations. We shall come to call these equations eigen-equations.
This now is just two simple problems.
The \(P\) modes
The \(P\) equation: \[ \deriv{P}{\theta}{2} = -\lambda_\theta P \]
This is the same eqution as we had for \(X\) and \(Y\) in the Cartesian case above. We saw that, depending on the sign of \(\lambda_\theta\) we expect trigonmetric (\(\sin\) or \(\cos\)), exponential or linear solutions. I think it should be clear that the periodic boundary conditions means we can only have \(\cos\) and \(\sin\) solutions as they are the only periodic functions.
The minus sign means trigonometric solutions are assoicated with a positive value for \(\lambda_\theta\) this is why the use of a minus sign in eigenproblems such as this is a common practice.
We then write our solutions as, \[ P(\theta) = A\cos\left(\sqrt{\lambda_\theta} \theta\right) + B \sin\left(\sqrt{\lambda_\theta} \theta\right). \] The periodic boundary conditions require: \[ A\cos(0) + B \sin(0) = A = A\cos\left(2\sqrt{\lambda_\theta} \pi\right) + B \sin\left(2\sqrt{\lambda_\theta} \pi\right), \] where we need the \(\cos\) term to equal \(1\) and the \(B\sin\) term to go to \(0\). For the former we require \(2\sqrt{\lambda_\theta} \pi=2 n \pi,\) so \(\sqrt{\lambda_\theta}\) must be an integer, that is \(\sqrt{\lambda_\theta} = n\), \(n=0,1,2,3,\dots\).
So the solution for \(P\) is, \[ P(\theta) = A\cos(n \theta) + B \sin(n \theta),\quad n=0,1,2,\dots, \] where we note that \(\lambda_\theta = n^2\). The inclusion of \(n=0\) covers the case that \(\lambda_\theta=0\), which has the constant solution \(P =A\). You should check this would also satisfy the derivative conditions
The \(R\) modes After expanding the derivative terms and multiplying by \(r^2\) the equation for \(R\) is:, \[ r^2\deriv{R}{r}{2} + r \dds{R}{r} +( \lambda r^2-n^2)R = 0, \] where the \(n^2\) comes from the fact the P boundary conditions ensured that \(\lambda_\theta=n^2\) and hence represents a coupling of the two boundary-value-problems.
The equation \[ r^2\deriv{R}{r}{2} + r \dds{R}{r} +( \lambda r^2-n^2)R = 0, \] is called Bessel’s equation. You solve it using the Frobineus method (seek a power series solution and find the coefficients) which you encountered in Calculus 1. You will not have to use it on this course. We are focusing on more fundamental properties aspects of PDE solution and this would be an unecessary distraction (you will recall its very time consuming!).
At this stage its worth highlighting some of the properties of Bessel functions, in particular some of the properties they share with the \(\sin\) and \(\cos\) functions. It will speak to the significant generalisations of this solution method which we study in the next chapter.
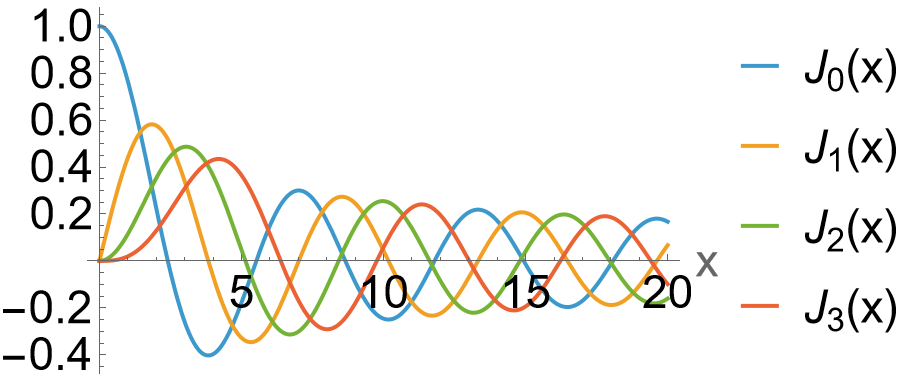
The Bessel functions of the first kind, \(J_n(x)\), arise as regular (finite at the origin) solutions to the Bessel differential equation, \[ x^2 \ddy{^2y}{x^2} + x \ddy{y}{x} + (x^2 - n^2)y = 0, \] where \(n\) may be an integer or real number (in the case at hand its an integer). The cases \(n=0,1,2,3\) are shown above. We see they are oscilliatory like the sin and coseine functions, but the amplitude decays. The remaining cases have these properties also.
Series representation
For integer order \(n\), \(J_n(x)\) admits a convergent power series solution around \(x=0\), \[ J_n(x) = \sum_{m=0}^\infty \frac{(-1)^m}{m!\,\Gamma(m+n+1)}\left(\frac{x}{2}\right)^{2m+n}, \] where \(\Gamma(\cdot)\) is the Gamma function.
Critical point: there is one function for each integer \(n\) which correspond to the different \(\theta\) modes \(\cos(n\theta),\sin(n\theta)\).
Derivatives
Bessel functions satisfy several useful recursion relations: \[\begin{align} \ddy{}{x}\!\big[x^n J_n(x)\big] &= x^n J_{n-1}(x),\\ \ddy{}{x}\!\big[x^{-n} J_n(x)\big] &= -x^{-n} J_{n+1}(x), \end{align}\]
Critical point: this is the equaivalent of \(d/dx \sin(x) = \cos(x)\) and \(d/dx \cos(x) = -\sin(x)\) (but sadly not as simple)
Countable infinity of zeros ## Bessel functions and their properties
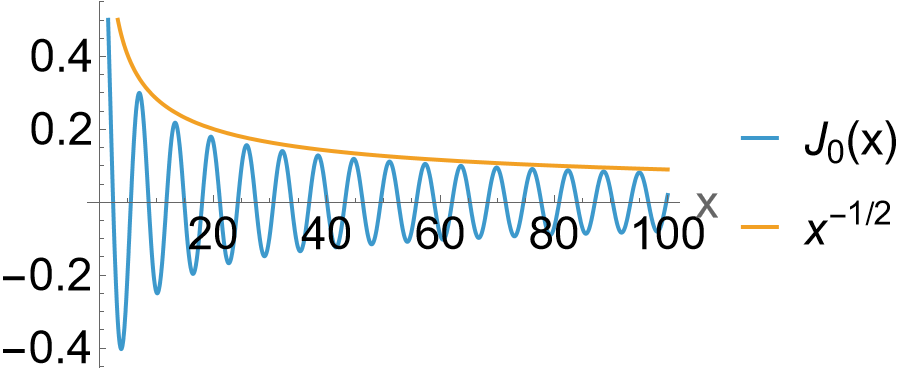
As indicated in the figure above, there are a countable infinite of zeros for each \(J_n(x)\)
Critical point: the zeros of sin and cos allowed them to satify homogenous boundary conidtions in the Cartesian (box) domain, which is why they formed the modes for the heat equation solution. This same property allows the Bessel functions to play the same role in this disc domain.
Orthogonality and zeros
The functions \(J_n(x)\) are orthogonal on the interval \([0,L_r]\) with respect to the weight \(x\), over their zeros \(j_{n,k}\): \[ \int_0^{L_r} x\, J_n\!\left(\frac{j_{n,k}x}{L_r}\right) J_n\!\left(\frac{j_{n,m}x}{L_r}\right)\,dx = \frac{L_r^2}{2}\,\big[J_{n+1}(j_{n,k})\big]^2\,\delta_{km}. \]
The zeros, \(j_{n,k}\) \(J_n(j_{n,k})=0\) determine the eigenvalues \(\lambda_{n,k} = (j_{n,k}/L_r)^2\) for problems on a disc.
Critical point: This is the Bessel equivalent of the Fourier ortogonality, e.g. \[ \frac{2}{L}\int_{0}^{L}\sin\left(\frac{n \pi}{L} x\right)\cos\left(\frac{m \pi}{L} x\right)d x = \delta_{nm}. \] It is used to create the so called Fourier-Bessel series.
“Fun” fact
There is a \(>800\) page book called the Treatise on Bessel functions authored in the 1920’s by G N Watson. This is what people did for fun back in the days before social media.
Finally, we do not yet have the values for the infinity of \(\lambda_n\) we should expect. These can be obtained by using the \(R\) boundary condition, \[ R_n(L_r)=0 \implies J_n(\sqrt{\lambda_{n}}L_r) = 0. \] We know they exist (though don’t have a nice clean formula). As these values may be different for each \(n\), we modify the subscript of our spatial eigenvalue to include this dependence and write \(\lambda_{k,n}\). Hence the solution for \(R_n\) in full generality can be written as, \[ R_n(r) = \sum_{k=1}^\infty A_{k,n}J_n\left(\sqrt{\lambda_{k,n}}r\right). \] We have chosen to index these zeroes starting at \(k=1\), but this choice is somewhat arbitrary, and just indicates that this first zero of \(J_n(x)\) is not in general \(x=0\) itself (though it will be for \(n>0\)).
General spatial eigenmodes for variation of \(u\) The only non-trivial (non-zero) spatial eigenmodes of the solution \(u\) are: \[ \Phi(r,\theta) = \sum_{n=0}^\infty \sum_{k=1}^\infty J_n\left(\sqrt{\lambda_{k,n}}r\right)\left(A_{k,n}\cos(n\theta) + B_{k,n}\sin(n\theta) \right), \] with combined spatial eigenvalue \(\lambda_{kn}\) being the zeros of the Bessel functions: \(J_k(\lambda_{kn})=0\).
Step 3: Solve for the temporal modes and construct the full sum
The temporal eigen-equation takes the form: \[ T'(t) +D\lambda_{kn}T(t) =0. \Rightarrow T_{kn}(t) = C_{k,n}\mathrm{e}^{-D\lambda_{kn}t}. \] So:
General separated solution (no initial conditions imposed yet)
Assembling all modes the solution to the heat equation: \[ \ddy{u}{t} = D\nabla^2u,\quad u(L_r,\theta,t)=0. \] is: \[\begin{align} u(x,y,t)&=\sum_{n=0}^\infty \sum_{k=1}^\infty T_{kn}(t)\Phi_{kn}(x,t)& \\&=\sum_{n=0}^\infty \sum_{k=1}^\infty\mathrm{e}^{-D\lambda_{kn}t} J_n\left(\sqrt{\lambda_{k,n}}r\right)\left(A_{k,n}\cos(n\theta) + B_{k,n}\sin(n\theta) \right). \end{align}\]
The Fourier–Bessel series
To completely determine the solution, we specify an initial condition
\[u(r,\theta,0)=f(r,\theta),\]
which fixes the constants \(A_{k,n}\), \(B_{k,n}\) in the expansion at \(t=0\): \[
f(r,\theta)
= \sum_{n=0}^{\infty}\sum_{k=1}^{\infty}
J_n\!\left(\sqrt{\lambda_{k,n}}\,r\right)
\Big[A_{k,n}\cos(n\theta)+B_{k,n}\sin(n\theta)\Big].
\]
To do this we use the radial (Bessel) orthogonality: \[ \int_0^{L_r} r\,J_n\!\left(\sqrt{\lambda_{k,n}}\,r\right) J_n\!\left(\sqrt{\lambda_{k',n}}\,r\right)\,dr = 0, \qquad k\ne k'. \] and angular (Fourier) orthogonality: \[ \int_0^{2\pi}\!\cos(n\theta)\cos(m\theta)\,d\theta =\int_0^{2\pi}\!\sin(n\theta)\sin(m\theta)\,d\theta =\pi\,\delta_{mn}, \qquad \int_0^{2\pi}\!\cos(n\theta)\sin(m\theta)\,d\theta=0. \]
To extract, say, \(A_{k,n}\), we multiply both sides of the expansion for \(f(r,\theta)\) by
\(r\,J_n(\sqrt{\lambda_{k,n}}r)\cos(n\theta)\) and integrate over the full domain:
\[\begin{align} &\int_0^{2\pi}\!\!\int_0^{L_r} r\,f(r,\theta)\, J_n\!\left(\sqrt{\lambda_{k,n}}\,r\right)\cos(n\theta)\,dr\,d\theta,\\ & = \int_0^{2\pi}\!\!\int_0^{L_r} r\,\sum_{n',k'}\! J_{n'}\!\left(\sqrt{\lambda_{k',n'}}r\right) \Big[A_{k',n'}\cos(n'\theta)+B_{k',n'}\sin(n'\theta)\Big] J_n\!\left(\sqrt{\lambda_{k,n}}\,r\right)\cos(n\theta)\,dr\,d\theta. \end{align}\]
Using the orthogonality relations: - all terms vanish except those with \(n'=n\) and \(k'=k\), - cross terms between sine and cosine also vanish.
Thus we obtain \[ \pi\,A_{k,n}\!\int_0^{L_r} r\, \big[J_n\!\left(\sqrt{\lambda_{k,n}}\,r\right)\big]^2\,dr = \int_0^{2\pi}\!\!\int_0^{L_r} r\,f(r,\theta)\, J_n\!\left(\sqrt{\lambda_{k,n}}\,r\right)\cos(n\theta)\,dr\,d\theta. \]
Hence \[ A_{k,n} =\frac{\displaystyle \int_0^{2\pi}\!\!\int_0^{L_r} r\,f(r,\theta)\, J_n\!\left(\sqrt{\lambda_{k,n}}\,r\right)\cos(n\theta)\,dr\,d\theta} {\displaystyle \pi\!\int_0^{L_r} r\, \big[J_n\!\left(\sqrt{\lambda_{k,n}}\,r\right)\big]^2\,dr}. \]
Repeating with \(r\,J_n(\sqrt{\lambda_{k,n}}r)\sin(n\theta)\) yields \(B_{k,n}\): \[ B_{k,n} =\frac{\displaystyle \int_0^{2\pi}\!\!\int_0^{L_r} r\,f(r,\theta)\, J_n\!\left(\sqrt{\lambda_{k,n}}\,r\right)\sin(n\theta)\,dr\,d\theta} {\displaystyle \pi\!\int_0^{L_r} r\, \big[J_n\!\left(\sqrt{\lambda_{k,n}}\,r\right)\big]^2\,dr}. \]
I introduced this method to apply the inital condition, but actually what I showed you is that any function \(f(r,\theta)\) on the disc (which is zero on the boundary) can be represented by a Fourier-Bessel series: \[ f(r,\theta) = \sum_{n=0}^{\infty}\sum_{k=1}^{\infty} J_n\!\left(\sqrt{\lambda_{k,n}}\,r\right) \Big(A_{k,n}\cos(n\theta)+B_{k,n}\sin(n\theta)\Big). \] The Fourier series is used when the domain is a square or rectangle domian, but actually doesn’t work for disc domains. The Fourier-Bessel series is (one example) of a series one can use on the disc. Like the Fourier series it can represent any square integrable function on the disc.
This example is preparing you for the key point in this half of the course. There are a lot of infinite series which can be used to represent arbitrary functions in terms of simple functions. They are adapted to the domain shape, boundary conditions and the nature of the PDE (i.e. the type of behaviour they need to capture).
Problem 9 of problem sheet 1 gives you a chance to apply this orthogonality in practice and problem 10 of problem sheet 1 considers the heat equation on a spherical domain, introducing you to the twin joys of Spherical Bessel functions and the Legendre polynomials.
1.8 So what are the key takeaways of all of this?
There are a few points we need to reflect on and which we will generlise in the next chapter. But first a bit of notation.
1.8.1 The linear differential operator notation and superposition as a general property.
A linear partial differential equation (PDE) can always be written in the abstract form
\[ Lu = f, \]
where \(L\) is a linear differential operator acting on the function \(u(x_1, x_2, \dots, x_n)\) and \(f\) is some scalar function.
For example: - The heat equation:
\[
L=\ddy{}{t} -D\nabla^2 \Rightarrow Lu = \ddy{u}{t} - D \nabla^2 u = 0,
\] - The wave equation:
\[
L=\pder{}{t}{2} - c^2\nabla^2 \Rightarrow Lu = \pder{u}{t}{2} - c^2 \nabla^2 u = 0,
\] - Random example:
\[
L=\nabla^2 +\sin(x) \Rightarrow Lu = \nabla^2 u +\sin(x) u= -\rho.
\]
Linearity of the Operator
An operator \(L\) is linear if it satisfies both additivity and homogeneity, i.e.
\[ L[a u_1 + b u_2] = a\,Lu_1 + b\,Lu_2 \]
for any scalar constants \(a, b\) and any functions \(u_1, u_2\) in the domain of \(L\).
Consequence: The Principle of Superposition (again)
If \(Lu = 0\) (a homogeneous linear PDE), and \(u_1\) and \(u_2\) are both solutions, then any linear combination
\[ u = a u_1 + b u_2 \]
is also a solution: \[ Lu = L[a u_1 + b u_2] = a L u_1 + b Lu_2 = 0. \]
Superposition is a general principle The property of linearity can be extended to an infinite sum, using induction, \[ L\left[\sum_{i=0}^{\infty} a_i u_i\right] = \sum_{i=1}^{\infty}a_iLu_i, \] and hence underlies all Fourier series and eigenfunction expansions for all linear PDE’s, not just the Heat equation.
Note this does of course assumes the infinite series converges (it will in the cases we conver this term).
1.8.2 Eigen-equations.
In the case of the heat equation, when using separation of variables, we ended up with the following ODE’s \[\begin{align} X''(x) = \lambda_x X,\quad Y''(y) = \lambda_y Y,\quad T'(t) = \lambda_t T \end{align}\] In the disc case we ended up with equations in the following form: \[\begin{align} \frac{1}{Rr}\dds{}{r}\left(r \dds{R}{r}\right) & = \lambda_{\vec{n}}-\frac{C_\theta}{r^2},\\ - \frac{1}{P}\deriv{P}{\theta}{2} = C_\theta, \end{align}\] Note that these equations are all in the following form: \[ L y(x) = \lambda r(x) y(x) \] Where \(L\) is a linear operator, \(\lambda\) a constant and \(r(x)\) some weighting funcion. This brings to mind the Matrix eigen-equation you encountered in Linear algebra:
\[ A \vec{v} = \lambda \vec{v}. \] where \(A\) is a matrix acting on a vector \(\vec{v}\) in a finite-dimensional space and \(\lambda\) is a scalar (the eigenvalue). In the case of a matrix equation we have \(n\) eigenvalues \(\lambda_i\) (for an \(n\) by \(n\) matrix) and \(n\) eigenvectors \(\vec{v}_i\).
In the case of the heat equation we had equations which looked like \[ L y(x) = \lambda y(x) \Rightarrow \deriv{y}{x}{2} =\lambda y(x). \] So the weight function \(r(x)\) is \(1\) and \(L = \deriv{}{x}{2}\), and we found a countable infinity of eigenvalues \(\lambda_i\) for the eigen functions \(\cos(\sqrt{\lambda_i} x)\) and \(\cos(\sqrt{\lambda_i} x)\) for given boundary conditions. So we have what we might call (and indeed do) an infinite dimensional “vector” space with eigenvalues.
Its all eigenequations silly
I am preparing you for the fact that ultimately, the vast generalisations we make in the following chapter of the ideas introduced in this chapter, all boil down to studying the properties of the weighted eigen-equaiton: \[ L y(x) = \lambda r(x) y(x) \] with the funciton \(r(x)\) typically playing the role of the domain geometry.
Consider another interestng example, the Cauchy-Euler equation in question 11 of problem sheet 1.
1.8.3 Are our infinite sums enough?
Consider the following function. \[\begin{align} u^c(x,y,t)&= \frac{a_{nm}}{4\pi D t} \Bigg[ e^{-\frac{(x-2mL_x)^2+(y-2nL_y)^2}{4D t}} + e^{-\frac{(x+2mL_x)^2+(y-2nL_y)^2}{4D t}}\\ &+ e^{-\frac{(x-2mL_x)^2+(y+2nL_y)^2}{4D t}} + e^{-\frac{(x+2mL_x)^2+(y+2nL_y)^2}{4D t}} \Bigg]. \end{align}\] for some integers \(n,m\).
Confirm by direct differentiation that \(u^c\) solves the heat quation: \[ \ddy{u^c}{t} = D\left(\pder{u^c}{x}{2} + \pder{u^c}{y}{2}\right). \] Subject to homogenous Neumann boundary conditions
We saw earlier that the following infite series also solves this equation: \[ u(x,y,t) = \sum_{n=0}^{\infty}\sum_{m=0}^{\infty}C_{nm}\mathrm{e}^{-D\left(\frac{n^2\pi^2 }{L_x^2} +\frac{m^2\pi^2 }{L_y^2} \right)t}\cos\left(\frac{n\pi x}{L_x}\right)\cos\left(\frac{m\pi y}{L_y}\right) \] This second solution is the sum of obviously separable functions (it is in the form \(T(t)X(x)Y(y)\)). We obtained a separable solution precisely because we made the separation ansatz. The first soltion, however, does not obviously seem separable due to the quotient of \((x-2mL_x)^2+(y-2nL_y)^2/4D t\).
So, are there more solutions than just those obtained by separaton of variables? Its a very specific ansatz…..
If so, how many? When do we stop? Ideally we want the complete general solution, one which could represent any solution for the appropriate coefficients \(a_{nm}\).
I have good news, for the case of the heat equation we can represent \(u^c\) and indeed any solution to the heat equation as a Fourier series in the from: \[ u^c(x,y,t) = \sum_{n=0}^{\infty}\sum_{m=0}^{\infty}c_{nm}(t)\cos\left(\frac{n\pi x}{L_x}\right)\cos\left(\frac{m\pi y}{L_y}\right) \] where \[ c_{mn}(t)=\frac{4}{L_xL_y}\!\int_{0}^{L_x}\!\!\int_{0}^{L_y} u^c(x,y,t)\cos\!\Big(\frac{m\pi x}{L_x}\Big)\cos\!\Big(\frac{n\pi y}{L_y}\Big)\,dy\,dx. \] So actually our apprently non-separable solution has a representation in terms of the infinite series. In fact one can show the following:
Proposition 1.1 Any solution to the Heat equation on \([0,L_x]\times[0,L_y]\) any boundary conditions and initial condition,can be represented in the form:
\[\begin{align} u(x,y,t) &= \sum_{m=0}^{\infty}\sum_{n=0}^{\infty}\mathrm{e}^{-D\left(\frac{n^2\pi^2 }{L_x^2} +\frac{m^2\pi^2 }{L_y^2} \right)t}\Big[ a_{mn}\cos\!\Big(\frac{m\pi x}{L_x}\Big)\cos\!\Big(\frac{n\pi y}{L_y}\Big) + b_{mn}\cos\!\Big(\frac{m\pi x}{L_x}\Big)\sin\!\Big(\frac{n\pi y}{L_y}\Big) \\ &+ c_{mn}\sin\!\Big(\frac{m\pi x}{L_x}\Big)\cos\!\Big(\frac{n\pi y}{L_y}\Big) + d_{mn}\sin\!\Big(\frac{m\pi x}{L_x}\Big)\sin\!\Big(\frac{n\pi y}{L_y}\Big)\Big]. \end{align}\]
The proof requires a lot more material than we have right now. In particular the completeness angle (all solutions). It basically rests on two facts. 1. The Fourier series can represent any square integrable function. 2. One can show that the solutions to the heat equation must be square intgerable.
In the next chapter we will make a start on the maths tools required to deirve such results (function spaces and norms, eigen expansions).
Okay so in the case of the heat it all works out, but that is only one equation. We have seen that the heat equation on a disc domain has a solution in terms of Bessel functions, in that case also it can be shown the infinte series is enough in that case. This begs the question Is separation of variables and the infinite sums they produce enough.
The answer is no sadly. Firstly some equations are not separable:
A non-separable linear PDE on a rectangle \[ u_{xx} + u_{yy} + x\,u_y = 0. \]
This is linear and elliptic with a drift term that couples \(x\) into the \(y\)-derivative. We can see this by trying the seperation ansatz: \(u(x,y)=X(x)Y(y)\).
Dividing by \(XY\) gives \[ \frac{X''}{X} + \frac{Y''}{Y} + x\,\frac{Y'}{Y}=0. \] The last term depends on \(x\) but involves only \(Y\). For this to hold for all \(x\), you must have \(Y'=0\) (trivial) or a contradiction. Hence no nontrivial separation in \((x,y)\).
1.8.4 Eigen series (mode decompositions) are the fundamental mathematics here not separation of variables.
In the examples we discussed above it is stil the case that the solutions \(u(x,y,t)\) can be written in the form: \[ u(x,y,t) = \sum_{n=0}^{\infty}T_n(t)\phi(x,y), \] but the spatial eigenfunctions \(\phi(x,y)\) cannot be separated into functions of solely \(x\) and \(y\) dependence. They also have orthogonality propeties like the separable examples we have seen above.
But need more sophisticated tools if we want to be able to show this eigen-expansion exists and has the property of orthogonality.
So to motivate the next chapter.
One of the main aims of this term is to show that a large class of equations, crucial in physical and biological modelling, have solutions \(u({\bf x},t)\) in the following “generalised Fourier series” form: \[ u(x,t) = \sum_{n=0}^{\infty}T_n(t)S_n({\bf x}). \] That is some spatial function \(S_n(x)\) which describes the individual spatial shapes the solutions are made from, and, for each spatial function \(S_n\), some function \(T_n(t)\) which determines how it varies in time.
1.9 What about non-linear PDE’s ?
The eagle-eyed student will note that:
- We have largely discussed linear methodologies, and in particular the notion of superposition
- A number of the interesting examples above are non-linear.
So does any of this apply to non-linear PDE’s, which generally are the more realistic models? Well most non-linear PDE’s have to be treated using numerical methods. A common class are spectral methods, which use a Fourier series expansion. The equations for the coefficients are more complicated (not just time dependent) but the idea of solving an equation using simpler linearly indpendent functions is an important one. In fact there are lots of spectral methods using lots of different “basis functions”, most of which are derived from the solution to linear equations.
In short the linear methods we mostly focus on in this course are a fundamental start point for the analysis of the more complex non-linear partial differential equations.