Description
Lie algebras, their structure and representations are of ubiquitous importance throughout mathematics and mathematical physics. The aim of this project is to understand semisimple Lie algebras (over the complex numbers) through their associated root systems, which are algebro-combinatorial gadgets that capture the structure of the Lie algebra. Semisimple Lie algebras 'decompose' into their 'simple' parts, so that we can consider so-called simple Lie algebras and their root systems.
Roughly speaking, a root system is a finite set of vectors in a real vector space with nice geometric properties (for example, it is invariant under certain reflections). Here are pictures of two of the simplest root systems. The one on the left is called $A_2$ and the one on the right is called $G_2$. They are each generated by two vectors $\alpha$ and $\beta$:
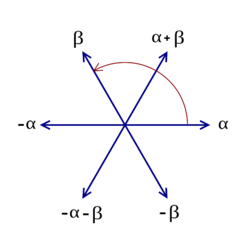
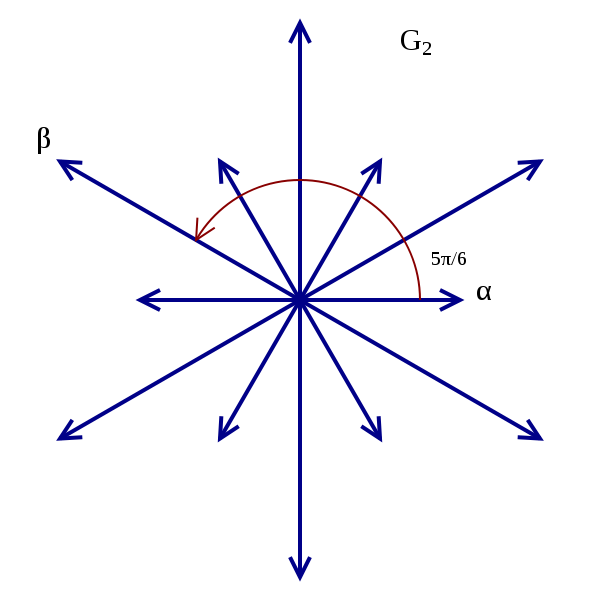
First, we will look at root systems in their own right, study some of their properties, and understand some of the ingredients leading to the classification of irreducible root systems via a special type of graphs called Dynkin diagrams. The irreducible root systems are classified into four infinite series $$A_n,B_n,C_n,D_n$$
together with five "exceptional" types
$$E_6,E_7,E_8, F_4, G_2.$$
These correspond to the Dynkin diagrams:

We will then study the basics of the theory of Lie algebras over the complex numbers. The aim here is to understand what a (semi-)simple Lie algebra is and how to construct a root system from it.
Finally, there are several possible further directions for individual study: Lie groups, Finite simple groups of Lie type (finite matrix groups associated to root systems, playing a fundamental role in group theory), Further properties and structure of Lie algebras, Lie algebras of affine type (see the books by Erdmann-Wildon and Carter).
Prerequisites
Algebra IICo-requisites
Representation Theory IVResources
- C. Laval, Root Systems: Classification, Construction, and Consequences, link.
- K. Erdmann and M. Wildon, Introduction to Lie Algebras.
- R. Carter, Lie Algebras of Finite and Affine Type.
- R. Carter, Simple groups of Lie type.