Description
The platonic and Archimedean solids have been known for well over 2000 years. They are assemblies of regular polygons so that all their vertices are equivalent to each others. The faces of the Platonic solids are also equivalent to each others. These regularities makes then visually aesthetic.
Polyhedral cages (p-cages) are assemblies of regular, or nearly regular, polygons with holes between them as, of two adjacent edges of a polygon, at most one of them can be shared with another face. When the faces are equivalent to each others, p-cages are very attractive visually and provide a large number of aesthetic structures.
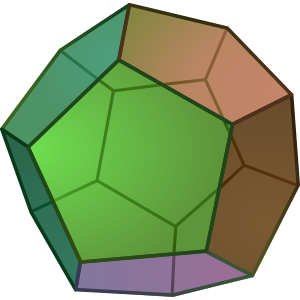
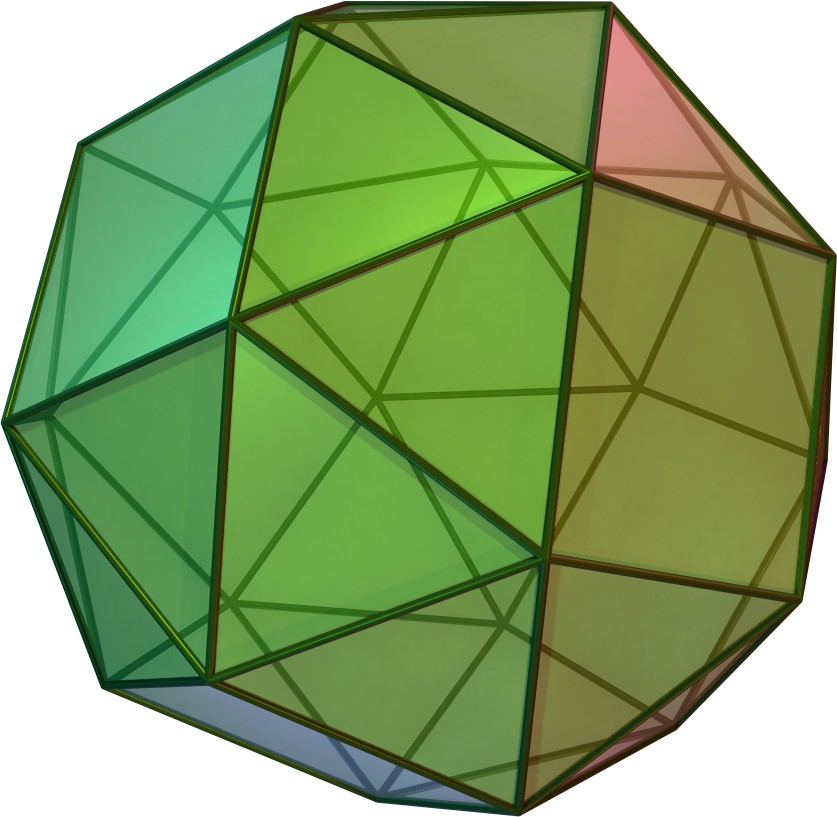
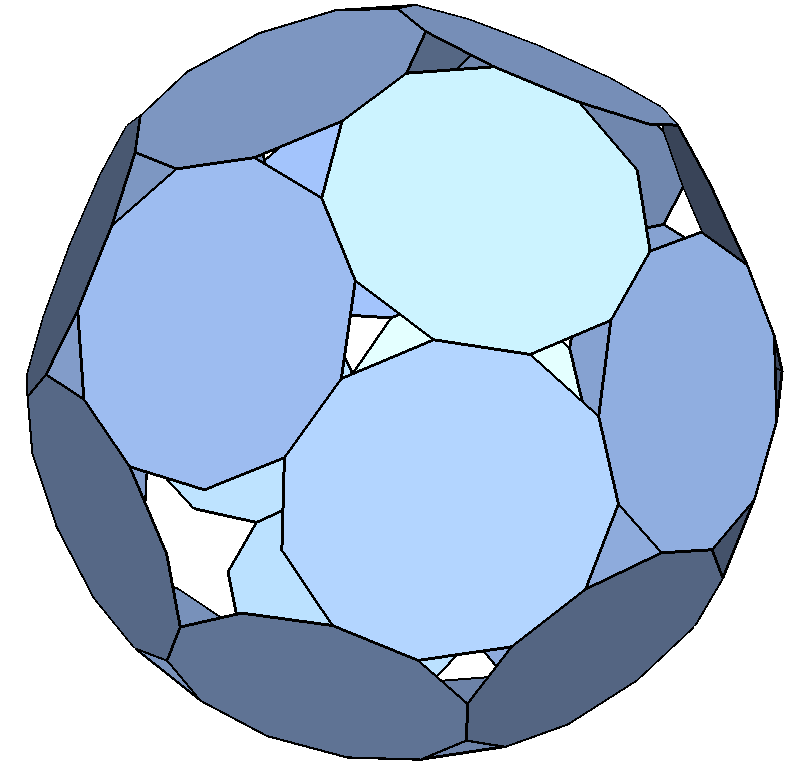

The aim of the project will be to study the mathematics behind these solids. It involves simple algebra and some Euclidean geometry in 3 dimensions including the extensive use of trigonometry and some simple group theory.
The project can involve some programming in python to generate 3 dimensional files to visualise different solids and how they can be morphed into each others.
Prerequisites
- There are no specific prerequisite for this module other than all the core modules as well as enjoying performing explicit algebraic and trigonometric calculations.