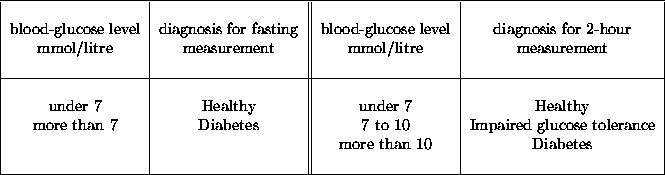
Figure 1: Oral glucose tolerance tests: diagnosis threshholds
Our example concerns the oral glucose tolerance test (ogt-test), used as an indicator of diabetes. The ogt-test is intended to measure the time taken to absorb a given quantity of sugar, with high values indicating diabetes. The test involves measuring the blood-glucose level in mmol/litre before and after a fixed quantity of sugar is taken orally (after fasting for twelve hours). Typically the blood glucose level is measured immediately prior to, and two hours after, the sugar is swallowed. Additionally, measurements might be made at intervening half-hour points. The most frequently utilised measurements are the fasting and two-hour measurements, taken before and two hours after ingestion of the sugar, and a well-established diagnosis of diabetes depends only upon these two measurements. Threshholds for the various diagnoses are given in figure 1.
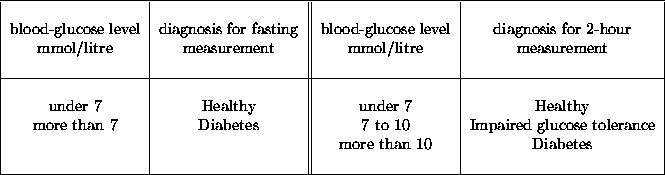
Figure 1: Oral glucose tolerance tests: diagnosis threshholds
We examine the efficacy of the ogt-test in relation to elderly people (for our purposes, people at least 60 years old). Previous trials of the ogt-test dealt largely with younger people, but there is a suspicion that the threshholds that indicate diabetes in a young person are inappropriate for older people. In particular, it is possible that the two-hour diagnosis threshhold is set too high for the elderly because their bodies react more slowly in general, and so take longer to absorb sugar. As a consequence, it is suspected that the ogt-test might often misdiagnose impaired glucose tolerance or diabetes in healthy elderly patients.
For our chosen scenario we suppose that an elderly lady doctor is
interested in the adequacy of the test for older people, and that she
decides to administer the ogt-test on herself to obtain further
information. To help organise her thoughts, she writes down the
quantities ![]() and
and ![]() , representing respectively the blood
glucose levels measured before and two hours after swallowing the sugar.
She thinks of each as a measurement on a randomly chosen elderly person,
presumed healthy and non-diabetic. Corresponding to these quantities,
she considers the measurements that she will make upon herself, and
writes these down as
, representing respectively the blood
glucose levels measured before and two hours after swallowing the sugar.
She thinks of each as a measurement on a randomly chosen elderly person,
presumed healthy and non-diabetic. Corresponding to these quantities,
she considers the measurements that she will make upon herself, and
writes these down as ![]() and
and ![]() . Thus
. Thus ![]() and
and
![]() are the (observable) before-and-after measurements that she
makes on herself; whereas
are the (observable) before-and-after measurements that she
makes on herself; whereas ![]() and
and ![]() are the (unobservable)
before-and-after measurements for an elderly person picked at random.
Our Doctor's aim is to learn about
are the (unobservable)
before-and-after measurements for an elderly person picked at random.
Our Doctor's aim is to learn about ![]() ,
, ![]() , and various
linear combinations such as
, and various
linear combinations such as ![]() , via
, via ![]() and
and ![]() .
Informally you might think of the former pair as characterising a
typical member of the (elderly) population; and the latter pair as a
``sample'' from that population.
.
Informally you might think of the former pair as characterising a
typical member of the (elderly) population; and the latter pair as a
``sample'' from that population.
At this point we will introduce some notation. We only distinguish between collections of quantities, which we term bases, and the more formal organisation of such collections as vectors of quantities, when this is not clear from the context. Thus we will refer both to the bases
![]()
and to the vectors ![]() and
and ![]() defined to be
defined to be
![]()
As we shall see, our approach allows us to obtain general impressions about collections of quantities as well as individual quantities, and when taking such a wider view we use the following notation:
The minimum specifications that we require for an analysis are expectations, variances and covariances over all the quantities of interest. If we intend (as we do) to produce adjusted expectations (informally, revisions) then we need some observations as well.