Every additional adjustment has the potential to reduce further the
uncertainty in our quantities of interest. The extra variance reductions
due to these partial adjustments are called partial resolved variances.
When we adjust by 
in addition to 
, the extra
reductions in variance for 
and 
are as follows:
with resolutions
Thus, the partial effect of adjusting by additionally is
negligible: relative to the initial uncertainty in , we achieve
a further reduction in uncertainty of only some 1.18%, and the relative
reduction in variance for is smaller still.
We may also evaluate the reductions in uncertainty relative to the
adjustment variances for the current adjustment:
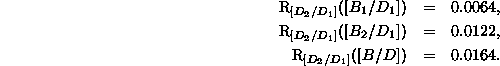
Thus, relative to the adjusted variances calculated for the initial
adjustment, 
, we see reductions of only 0.64% and
1.22% for and respectively; and relative to the
former adjustment uncertainty 
a further reduction in
uncertainty for the overall belief structure 
of only 1.64%. The
conclusion seems quite clear: from the point of view of reducing
uncertainties, as an additional source of information is
almost worthless; alone carries most of the information.
The notation that we use here, 
for example,
reflects the fact that after the initial adjustment by , it is
as though we focus attention on the portion of that remains
uncertain, namely 
, the adjusted version of
given . Now a partial adjustment by 
of the
original quantity is equivalent to an initial adjustment of
the adjusted version (which has prior variance 
) by .