Now, we are interested not only in how we obtain our adjusted
expectations for 
and 
, but also in how valuable the
adjustment is in terms of reducing uncertainty. To this purpose we
examine the adjusted variances: in terms of our general notation we have
approximately
Here, 
is our notation for the uncertainty remaining in
in the light of the information contained in 
, so we
expect uncertainty in to reduce from 
to
; and the uncertainty in to reduce
from 
to 
. We call the
difference between these two values the resolved variance, and we also
determine the resolution, which is a scale-free measure of the
reduction in variance. For the belief structure taken as a whole we can
determine analagous results.
For each quantity, we can decompose the initial variation into
portions remaining and resolved. For the decomposition is
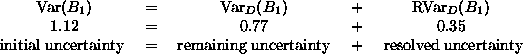
For the decomposition is
The resolution for each quantity can lie between zero and unity
inclusive, with a resolution of zero implying that we expect the
adjustment to be completely uninformative, and a resolution of unity
implying that we expect the adjustment to be completely informative. For
our two quantities and we obtain
which tells us that by adjusting on , we reduce the uncertainty in
by about 31%, and we reduce the uncertainty in only
by about 5%. The adjustment is informative in only a limited sense for
, and hardly at all for .