| Mikhail Agranovich (Moscow Institute of Electronics and Mathematics) | Monday 8th August 09:20 |
| Poincare-Steklov type operators in domains with Lipschitz boundaries
|
| We consider a strongly elliptic second order system in a bounded domain. The
principal part of the system is written in a divergent form, but the system is
not necessarily self-adjoint. The boundary conditions are mixed and contain the
spectral parameter on a part of the boundary. Assuming that the domain is
Lipschitz, we consider the problem in the variational setting by means of the
classical variational approach and describe some spectral properties of the
corresponding Neumann-to-Dirichlet type operators in the simplest Sobolev
spaces. These operators admit more explicit representation if it is possible to
use surface potentials, in particular if the coefficients in the system are
constant. The information is more complete in the case of N-to-D operators on
the whole boundary. In the general case, assuming additional smoothness, we
use the Wiener-Hopf method. Similar approaches are used for exterior mixed
problems. In addition, we consider transmission spectral problems in the case
of a non-closed boundary. A lot of references will be given in the talk.
|
|
| Charles Batty (University of Oxford) | Saturday 6th August 17:10 |
| Resolvent conditions for perturbations of semigroup generators and
solutions of delay equations |
| There are well known results of the form that if $A$ generates a
$C_0$-semigroup of a certain type and $B$ is a perturbation of a certain
type then $A+B$ generates a $C_0$-semigroup. We give some converse results
for generators of semigroups and related operators, and some results about
differentiability of solutions of delay equations. |
|
| Michael Berry (University of Bristol) | Wednesday 10th August 11:50 |
| Physics of nonhermitian degeneracies |
| Decoherence makes quantum evolution nonunitary, and
such systems, where some freedoms are ignored, can be described by
nonhermitian hamiltonian operators. These differ most dramatically from
hermitian operators in the neighbourhood of degeneracies. Several
examples of non-hermitian degeneracy-dominated physical phenomena will
be given, in laser physics, atom optics, and crystal optics. |
|
| Albrecht Boettcher (TU Chemnitz) | Monday 8th August 11:50 |
| From Toeplitz eigenvalues to spectra of canonical
higher-order ordinary differential operators |
The talk is concerned with a sequence of constants
which appear in
several problems. These problems include the minimal eigenvalue of
certain
positive definite Toeplitz matrices, the minimal eigenvalue of some
higher-order
ordinary differential operators, the norm of the Green kernels of these
operators, the best constants in Wirtinger-Sobolev inequalities, and
the conditioning of a special least squares problem. We give an
introduction to all these topics, discuss the asymptotics of the
sequence, and disclose the mystery
of the appearance of some regular numbers in the spectra of certain
differential operators.
The talk is based on joint work with Harold Widom. |
|
| Lyonell Boulton (Heriot-Watt University) | Wednesday 3rd August 10:20 |
| On the oscillation of eigenfunctions of fourth-order two-point boundary value problems. |
| It is well known that the notion of conjugate
points for linear systems of ordinary differential equations, allows us
to characterise oscillation properties of solutions of boundary value
problems of order greater than two. However, in the general case, a
conjugate point need not be a place where the solution vanishes.
In this talk we consider counting true zeros of solutions. Our main
goal will be to discuss how to recover results in the spirit of the
classical Sturm-Liouville theorem for fourth-order eigenvalue problems. |
|
| Simon Chandler-Wilde (University of Reading) | Thursday 4th August 17:10 |
| Spectral problems associated with scattering by unbounded surfaces |
| We consider the problem of scattering of an acoustic wave by an unbounded
surface that is the graph of some bounded continuous function, f, and the
reformulation of this problem as a second kind integral equation with an
integral operator that depends on the function f as a parameter. We study
how the spectrum depends on f and on the function space on which the
operator acts, making connections with Floquet-Bloch theory in the case when
f is periodic, and with recent theories of generalised convolution
operators. |
|
| Walter Craig (McMaster University) | Thursday 4th August 11:50 |
| Hamiltonian PDE |
| Abstract: Many nonlinear evolution equations can be
posed as Hamiltonian systems with infinitely many degrees of freedom.
These include some of the central equations of mathematical physics;
the nonlinear wave equation, the nonlinear Schroedinger equation, the
Euler equations for free surfaces in fluid dynamics, and others. In a
neighborhood of an equilibrium, the linearized equations are those of a
harmonic oscillator and thus their solutions exhibit periodic,
quasi-periodic and almost periodic motion. To construct solutions of
the same nature for the nonlinear partial differential equations is a
small divisor problem in general. This talk will give an overview of a
variational principle which arises, and an overview of some of the
analytic techniques and results from Hamiltonian dynamical systems
applied to PDE, which have been developed to address this class of
problems. |
|
| Michael Dritschel (University of Newcastle) | Saturday 6th August 10:20 |
| Interpolation in semigroupoid algebras |
| A seminal result of Agler characterises the
so-called Schur-Agler class of functions on the polydisk in terms of a
unitary colligation transfer function representation. We generalise
this to the unit ball of the algebra of multipliers for a family of
test functions/reproducing kernels over a broad class of semigroupoids.
There is then an associated interpolation theorem. Besides leading to
solutions of the familiar Nevanlinna-Pick and Carathéodory-Fejér
interpolation problems and their multivariable commutative and
noncommutative generalisations, this approach also allows us to
consider more exotic problems, such as interpolation over domains where
the Pick condition is not satisfied and interpolation over a variety of
matrix algebras. |
|
| Des Evans (Cardiff University) | Friday 5th August 10:20 |
| On the spectrum in Smilansky's model of irreversible quantum graphs: the 2-oscillator case |
(Joint work with M. Solomyak)
In his
talk M.Solomyak has already discussed Smilansky's model and described
results established on the spectrum of the underlying self-adjoint
operator when the system involves one harmonic oscillator. In this talk
the analyic obstacles encountered in the case of two harmonic
oscillators will be discussed and recent results obtained jointly with
M. Solomyak given. |
|
| Edward Fraenkel (University of Bath) | Thursday 11th August 11:50 |
| A constructive existence proof for the extreme Stokes wave |
| A troublesome, non-linear integral equation is
solved in the following naive way. First, an explicit formula defines
an approximation with numerically small error; secondly, the Frechet
derivative at this approximation is inverted; thirdly, inequalities are
found for the non-linear remainder. There results a contraction map for
the difference between the exact solution and the approximation. |
|
| Leonid Friedlander (University of Arizona) | Friday 5th August 15:50 |
| The determinant of a differential operator on a metric graph |
| We derive a formula for computing the determinant
of an operator on a metric graph. In the case of the Laplacian, this
formula is rather explicit. |
|
| Alex Gamburd (Stanford University) | Tuesday 9th August 10:20 |
| Poisson-Dirichlet distribution for random Belyi surfaces |
| Brooks and Makover introduced an approach to
studying the global
geometric quantities (in particular, the first eigenvalue of the
Laplacian, injectivity radius and diameter) of a "typical" compact
Riemann surface of large genus based on compactifying finite-area
Riemann surfaces associated with random cubic graphs; by a theorem of
Belyi these are "dense" in the space of compact Riemann surfaces. The
question as to how these surfaces are distributed in the Teichmuller
spaces depends on the study of oriented
cycles in random cubic graphs with random orientation; Brooks and
Makover conjectured that asymptotically normalized cycles lengths
follow Poisson-Dirichlet distribution. We present a proof of
this conjecture using representation theory of the symmetric group. |
|
| Alastair Gillespie (University of Edinburgh) | Friday 5th August 17:10 |
| Weighted ergodic theory and dimension free estimates |
(Joint work with J.L. Torrea)
I shall discuss a weighted ergodic theory associated with a
strongly continuous one-paramenter group of positive operators acting on
an Lp space which parallels the classical Ap theory. This is then used to obtain dimension free weighted inequalities for certain classical operators. |
|
| Ilya Goldsheid (QMUL) | Thursday 4th August 17:40 |
| Random diffeomorphisms, Lyapunov exponents, and random operators |
| I shall discuss recent results about contraction
properties of
random diffeomorphisms acting on skew product spaces. It turns out
that these lead, in particule, to control of Lyapunov exponents of
products of random matrices. The latter, in turn, are responsible for
the spectral properties of random operators. |
|
| Oleksandr Gomilko (Kiev National University of Trade and Economics) | Thursday 11th August 17:40 |
| The Caley transform of the generator of a uniformly bounded C_0-semigroup |
|
|
| Gian Michele Graf (ETH-Zurich) | Saturday 6th August 11:50 |
| Equality of bulk and edge Hall conductances in a mobility gap |
(Joint work with A. Elgart, J. Schenker.)
I
will present two interpretations of the integer quantum Hall effect on
the basis of either bulk or edge currents, introduce the
corresponding conductances, and heuristically show that they are equal.
In a more strict part, I will consider quantum Hall systems for which
the Fermi energy falls in a band where bulk states are localized, this
being the prerequisite for a Hall plateau. After defining the edge
conductance in a manner appropriate to this situation, I will prove its
equality to the bulk value. |
|
| Rostyslav Hryniv (Institute for Applied Problems of Mechanics and Mathematics, NASU) | Wednesday 3rd August 17:40 |
| Inverse spectral problems for Bessel operators |
(Joint work with S Albeverio and YV Mykytyuk)
Let q be a real-valued distribution from the space W-12(0,1) and let S denote the Bessel operator on L2(0,1) given by
(Sy)(x) = - y"(x) + m(m-1)y(x)/x2 + q(x) y(x),
where m is a nonnegative integer. We study the inverse spectral problem
of reconstructing the operator S from two spectra corresponding to two
different boundary conditions at the endpoint x=1.
|
|
| Serguei Iakovlev (Simon Bolivar) | Poster |
| Operators of Friedrichs with a non-trivial singular spectrum |
|
|
| Ilia Kamotski (University of Bath) | Monday 8th August 18:10 |
| Structure of the spectrum of acoustic operator with
singularly perturbed periodic coefficients
|
| It is well known that one-dimensional Schrodinger operator with
periodic potential ``always" has band gaps in its spectrum. On the
contrary, in the multi-dimensional case such gaps are extremely
rare. On the other hand, their existence is of great importance,
for example for the presence of localised states in photonic
crystals. We consider 3D-homogenous acoustic media perturbed by
the set of small periodically distributed inclusions with high
compressibility. Previously known examples
of gaps for high contrast materials are where the contrast is
imposed either on thin films or on domains with asymptotically
non zero volume. We investigate media with small defects localised
in the neighborhood of isolated periodic set of points. This
allows us to observe an explicit asymptotic mechanism for opening
of the gaps. Using the method of matched asymptotic expansions we
demonstrate the existence of gaps, derive their asymptotics
and rigourously justify it. Further analysis of asymptotic
representation of solutions shows that such media can be modelled
by some operator with non-linear frequency dependence. This operator can be treated as an $L_2$ self-adjoint extension of the
governing operator originally defined on functions equal to zero
near the defects.
|
|
| Lev Kapitanski (University of Miami) | Saturday 6th August 15:50 |
| Geometry and analysis of the Faddeev model |
|
|
| Thomas Kappeler (Universität Zürich) | Friday 5th August 11:50 |
| On geodesic exponential maps of the Virasoro group
|
(Joint work with A. Constantin, B. Kolev, and P. Topalov)
We study the geodesic exponential maps corresponding to Sobolev type right-invariant
(weak) Riemannian metrics g(k) ( k = 0, 1, ...) on the Virasoro group Vir and
show that for k = 2, 3, 4,... , but not for k = 0, 1, each of them defines
a smooth Frechet chart of the unital element in Vir.
The geodesic exponential map for k = 0 corresponds to the KdV equation and hence
is not a local diffeomorphism near the origin.
|
|
| David Khmelnitskii (University of Cambridge) | Wednesday 3rd August 17:10 |
| Physicist's view on localisation
|
| The purpose of this talk is to present not rigorous prejudices
and believes physics community has about localisation in different
dimensions in magnetic field and without it.
|
|
| Boris Khoruzhenko (QMUL) | Monday 8th August 10:20 |
| Moments of spectral determinants of complex random matrices |
(Joint work with Y.V. Fyodorov)
Let A be
a fixed nxn matrix and U be a unitary matrix picked up at random from
the unitary group U(n). We express the integer moments of the spectral
determinant |\det(zI_n-AU)|^2 in terms of the characteristic polynomial
of the matrix AA^*. This result provides a useful tool for studying the
eigenvalue distributions of complex random matrices. Links between this
problem, Kaneko's generalization of the Selberg integral and
Zirnbauer's color-flavor transformation will be discussed. |
|
| Anna Kirpichnikova (Loughborough University) | Poster |
| Inverse Boundary Spectral Problem for a Riemannian Polyhedron |
|
|
| Vladimir Kisil (University of Leeds) | Thursday 4th August 10:20 |
| Algebraic and analytic aspects of covariant functional calculus |
| Covariant functional calculus is defined as an intertwining operator
between certain group representations [1, 2]. The intertwining
property replaces the algebraic homomorphism required by the standard
definition of functional calculus. This gives advantages in
consideration of non-normal operators [2] and enable functional
calculus of several non-commuting operators [1, 3]. Spectrum of
operator (or a n-tuple of operator) is defined as the
support of the functional calculus [2], i.e. collection of
nonvoid intertwining operators with primary representations.
The previous results [2, 3] was mainly dealing with finite-dimensional
operators and thus have essentially algebraic nature. The passage to
infinite dimensional operators highlights interesting analytic
structure in the category of intertwining operators.
[1] V.V. Kisil, Mobius transformations and monogenic functional
calculus, Electron. Res. Announc. Amer. Math. Soc. 2 (1996), no. 1,
2633, (electronic) MR 98a:47018.
[2] V.V. Kisil, Spectrum as the support of functional calculus,
Functional Analysis and its Applications (Proceedings of the S. Banach
Conference) (North-Holland) (V. Kadets and W. Zelazko, eds.),
Math. Studies series, vol. 197, Elsevier Science Publishers, 2004,
E-print: arXiv:math.FA/0208249, pp. 133142.
[3] V.V. Kisil, Monogenic calculus as an intertwining operator,
Bull. Belg. Math. Soc. Simon Stevin 11 (2005),
E-print: arXiv:math.FA/0311285. |
|
| Frédéric Klopp (Paris Nord) | Tuesday 9th August 11:50 |
| Resonances for slowly varying perturbations of a periodic Schrödinger operator |
| In this talk, we present recent results on the
width of the resonances for a slowly varying perturbation of a
one-dimensional periodic operator. It is based on joint work with M.
Marx. The perturbation is assumed to be analytic and local in the sense
that it tends to a constant at infinity; the constants at both
infinities may differ. Modulo an assumption on the relative position of
the range of the local perturbation with respect to the spectrum of the
background periodic operator, we show that the width of the resonances
is essentially given by a tunneling effect in a suitable phase space. |
|
| Vladimir Kozlov (Linköpings Universitet) | Thursday 4th August 15:50 |
| L2-perturbations of leading coefficients of elliptic operators: asymptotics of eigenvalues and similar problems |
|
|
| Pavel Kurasov (Lunds Universitet) | Thursday 11th August 17:10 |
| Wigner-von Neumann perturbations of periodic Schrödinger operator
|
(Joint work with S. Naboko
Wigner-von Neumann type perturbations of the one-dimensional
Schrödinger operator are considered. The asymptotics of the solution
to the generalized eigenfunction equation is investigated.
It is proven that the subordinated solution and therefore an
embedded eigenvalue may occur at the points on the continuous
spectrum satisfying a certain resonance (quantization) condition
between the frequencies of the perturbation, the frequency of the
potential and the corresponding quasimomentum. |
|
| Ari Laptev (KTH, Stockholm) | Monday 8th August 15:50 |
| Spectral inequalities for many particles |
| We consider a number of inequalities for
multi-particle Schrödinger operators. Optimal constants appearing in
such inequalities are related to some elementary problems from
geometrical combinatorics. |
|
| Michael Levitin (Heriot-Watt University) | Thursday 11th August 10:20 |
| Embedded eigenvalues of the Laplacian for domains with cylindrical ends |
(Joint work with M Marletta)
In a work motivated by a wide class of waveguide-type problems, we give some upper estimates on a number of eigenvalues embedded into the essential spectrum
of a Laplacian acting on a domain with cylindrical outlets to infinity.
We also construct a simple algorithm for finding such eigenvalues
numerically. The algorithm also applies to finding complex resonances, and allows an easy modification for other differential operators and infinite geometries. |
|
| Marko Lindner (TU Chemnitz) | Friday 5th August 10:50 |
| Generalized collective compactness and limit operators |
|
|
| Vitali Liskevich (University of Bristol) | Monday 8th August 10:50 |
| Gaussian bounds for propagators perturbed by potentials |
(Joint work with H. Vogt and J.Voigt)
We develop the perturbation theory for propagators, with the objective
to prove Gaussian bounds.
Let U be a strongly continuous propagator, i.e., a family of operators
describing the solutions of a non-autonomous evolution equation, on an
Lp-space, and assume that
U is positive and satisfies Gaussian upper and lower bounds. Let V be a (time-dependent) potential
satisfying certain Miyadera conditions with respect to U. We show that then the perturbed propagator
enjoys Gaussian upper and lower bounds as well. |
|
| Annemarie Luger (Vienna University of Technology) | Poster |
On eigenvalues of self-adjoint extensions
(Joint work with Jussi Behrndt, TU Berlin)
|
Let S be a symmetric operator (or relation) with finite defect index in some
space K and let A be a self-adjoint extension of S, which acts in a larger space K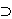 K.
Often (eg. if K is a Hilbert space) the compressed resolvent
PK(A-z)-1|K
is then given like in Krein's formula. In particular there appears a
parameter T(z) and m(z), the corresponding Q-function of a pair (A0,S) for some fixed self-adjoint extension A0 in K. K.
Often (eg. if K is a Hilbert space) the compressed resolvent
PK(A-z)-1|K
is then given like in Krein's formula. In particular there appears a
parameter T(z) and m(z), the corresponding Q-function of a pair (A0,S) for some fixed self-adjoint extension A0 in K.
It turns out that in this situation - under some additional assumption on the parameter T - the eigenvalues of A are given as the generalized zeros of the function m(z)+T(z).
Here the inner product on the space K need not be positive definite, however, locally we assume the existence of only finitely many negative squares.
Furthermore we point out the connection to an abstract boundary value
problem. |
|
| Marco Marletta (Cardiff University) | Friday 5th August 17:40 |
| Weak stability for an inverse Sturm-Liouville problem with finite
spectral data and complex potential |
We consider a stability result for the Sturm-Liouville equation with complex
potential in which the first N Dirichlet-Dirichlet eigenvalues and the first
N Dirichlet-Neumann eigenvalues are known to within a given error. Although the
problem is not uniquely solvable we show that all the complex potentials which
solve it are close in a suitable weak norm.
This is joint work with Rudi Weikard of University of Alabama at Birmingham. |
|
| Yuri Netrusov (University of Bristol) | Saturday 6th August 17:40 |
| Sharp version of the Birman-Solomyak theorem on estimates of
entropy numbers
|
|
|
| Nikolai Nikolski (Université Bordeaux) | Wednesday 3rd August 11:50 |
| Van der Waerden's problem and analytic capacities |
| We discuss condition numbers of nxn matrices with a
given lower bound of eigenvalues as n tends to infinity. The techniques
used are zero sets capacities of finite sets with respect to the ususal
holomorhic spaces, like some Besov spaces, or Beurling-Sobolev spaces. |
|
| Leonid Parnovski (University College London) | Tuesday 9th August 17:40 |
| Distribution of lattice points in Euclidean and hyperbolic spaces |
(Joint work with R.Hill)
We study the
number of lattice points inside a ball (or an annulus) of large
radius as a function of the centre of a ball. The average value of this
function is the volume of the ball, and we obtain upper and lower
bounds (and asymptotics in some cases) for the average deviation of
this function from its average as well as for its variance. |
|
| Jonathan Partington (University of Leeds) | Tuesday 9th August 10:50 |
| The resolvent test for admissibility of semigroups and Volterra equations
|
(Joint work with Birgit Jacob)
Consider the system [dx(t)/dt]=Ax(t), y(t)=Cx(t), for
t 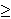 0,
where each x(t) lies in a
fixed Hilbert space H. Here the operator A with domain D(A) 0,
where each x(t) lies in a
fixed Hilbert space H. Here the operator A with domain D(A)
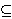 H
generates a contraction semigroup,
and C:D(A) H
generates a contraction semigroup,
and C:D(A)
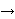
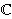 n
is a finite-rank observation operator. The property of admissibility,
||
y
(.)||L2(0, n
is a finite-rank observation operator. The property of admissibility,
||
y
(.)||L2(0,
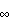 ) )
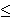 const.
||
x(0)
||, is known to be related (by the Weiss conjecture)
to the growth of
||
C(sI-A)-1
|| for s in the right half-plane: this theory extends
certain classical results on Hankel operators and Carleson embeddings. const.
||
x(0)
||, is known to be related (by the Weiss conjecture)
to the growth of
||
C(sI-A)-1
|| for s in the right half-plane: this theory extends
certain classical results on Hankel operators and Carleson embeddings.
We review these ideas, and provide an appropriate generalization to Volterra systems,
as well as a counterexample to the Weiss conjecture in this context. |
|
| David Pearson (University of Hull) | Thursday 4th August 10:50 |
| Spectral density for one-dimensional Schrodinger operators |
For various classes of potential q, there is a well
established link between spectral density of the corresponding
Schrodinger operator on the half line, subject to boundary condition at
x=0, and the large x asymptotics of quadratic forms in solutions of the
Schrodinger equation and their derivatives. Original results of this
kind are due to Titchmarsh in the case of potentials of L1 class.
This talk will present a general theory of quadratic forms in
solutions of the Schrodinger equation, and show how the theory may be
used to determine spectral density for wide classes of potential,
including in particular slowly decreasing potentials, periodic
potentials, and examples of Wigner-von Neumann type. The theory will
also be applied to the determination of spectral density for problems
with two singular endpoints. Some of the results obtained have been
implemented numerically in calculations of spectral density, in
collaboration with Charles Fulton and Steve Pruess. |
|
| Beatrice Pelloni (University of Reading) | Saturday 6th August 10:50 |
| The spectral analysis of linear differential operators - a new approach |
|
|
| Michael Plum (Universität Karlsruhe) | Thursday 4th August 09:20 |
| An existence and enclosure method for nonlinear elliptic boundary value problems |
| The lecture will be concerned with numerical
enclosure methods for nonlinear elliptic boundary value problems. Here,
analytical and numerical methods are combined to prove rigorously the
existence of a solution in some "close" neighbourhood of an approximate
solution computed by numerical means. Thus, besides the existence
proof, verified bounds for the error (i.e. the difference between exact
and approximate solution) are provided.
For the first step, consisting of the computation of an approximate
solution in some appropriate Sobolev space, no error control is needed,
so a wide range of well-established numerical methods (including
multigrid schemes) is at hand here. Using this approximate solution,
the given problem is written as a fixed-point equation for the error,
and the goal is to apply a fixed-point theorem providing the desired
error bound.
The conditions required by the chosen fixed-point theorem
(e.g., compactness or contractivity, inclusion properties for a
suitable subset etc.) are now verified by a combination of analytical
arguments (e.g., explicit Sobolev embeddings, variational
characterizations etc.) and verified computations of certain auxiliary
terms, in particular of eigenvalue bounds for the linearization of the
given problem at the approximate solution. The method is illustrated by
several examples (on bounded as well as on unbounded domains), where in
particular it gives existence proofs in cases where no purely
analytical proof is known. |
|
| Iosif Polterovich (Université de Montréal) | Wednesday 10th August 10:20 |
| The spectral function and the remainder in local Weyl's law: View from below |
| The talk focuses on asymptotic lower bounds for the
spectral function of the Laplacian and for the pointwise error term in
Weyl's law on manifolds. I will first discuss some general results and
then explain how the techniques of thermodynamic formalism for
hyperbolic flows yield stronger estimates in the negatively curved
case. This is a joint work with Dmitry Jakobson (McGill).
|
|
| Sandra Pott (University of Glasgow) | Thursday 11th August 10:50 |
| Admissibility and exact observability of observation operators |
| We discuss some new criteria for admissibility and
exact observability of observation operators on semigroups. (This is
joint work with J. Partington.) |
|
| Roman Romanov (St Petersburg State University) | Poster |
| Spectral singularities and asymptotics of contractive semigroups |
Joint work with Sergey Naboko
The problem of localization of spectral singularities of
dissipative operators in terms of the asymptotic of the
corresponding exponential function is studied. We give a solution
to this problem for the singularities of higher orders in the
frame of the perturbation theory. |
|
| Grigori Rozenblioum (Chalmers University of Technology) | Tuesday 9th August 09:20 |
| On eigenvalues of the Pauli and magnetic Schrödinger operators
with variable magnetic field: zero modes and splitting of Landau levels. |
|
|
| Michael Ruzhansky (Imperial College London) | Thursday 4th August 18:10 |
| Limiting absorption principle in the critical case and applications |
| In general, the limiting absorption principle allows one to deal with
resolvents of operators near the spectrum by taking limits in weighted
Sobolev spaces. We will talk about the critical cases of this where
one observes the propagation of singularities along trajectories
for the corresponding evolution equation.
Results will be applied to smoothing problems for Schrodinger equation
and to nonlinear equations with null-form structure.
The talk is based on the joint work with Mitsuru Sugimoto (Osaka). |
|
| Yuri Safarov (King's College London) | Poster |
| Multidimensional numerical range |
|
|
| Eugene Shargorodsky (King's College London) | Saturday 6th August 18:10 |
| The Riemann-Hilbert problem with a vanishing coefficient that arises in nonlinear hydrodynamics |
| The talk, based on joint works with J.F. Toland and with J. Virtanen,
will describe various (non)uniqueness results for the Riemann-Hilbert
problem in the case when the coefficient is continuous and is allowed
to vanish on an arbitrary closed set of measure zero. In most earlier
works the zero set of the coefficient was finite and the coefficient
had a simple power- or power-log-like behaviour in a neighbourhood of
its zeros. The motivation for the problems we consider comes from the
theory of Bernoulli free-boundary problems and, in particular, from
the variational theory of Stokes waves. |
|
| Stanislav Shkarin (King's College London) | Friday 5th August 18:10 |
| On possible spectral structure of linear continuous operators |
For a class X of topological vector spaces let
P(X) (resp. Q(X)) be the set of triples (A,B,C) of subsets of the
complex plane for which there exist E in X and a continuous (resp.
closed densely defined) linear operator T acting on E, for which A is
the point spectrum B is the continuous spectrum and C is the residual
spectrum. While it is usually relatively easy to find necessary
conditions for a triple (A,B,C) to belong P(X), the task to show that
this conditions are sufficient, is much more complicated. It can be
considered as a problem of spectral syntesis: for a given triple of
sets (A,B,C), satisfying certain conditions to find a space E in X and
an operator T acting on E such that A, B and C are exactly the parts of
the spactrum of T.
We characterize the sets P(Xn) and Q(Xn), n=1,2,3,4, where X1 is
the class of separable Hilbert spaces, X2 is the class of separable
reflexive Banach spaces, X3 is the class of separable Banach spaces and
X4 is the class of separable Frechet spaces.
For instance, the set P(X1)=P(X2) is exactly the set of triples
(A,B,C) of subsets of complex plane for which A is a countable union of
closed sets, B is a countable intersection of open sets and the union
of A, B and C is non-empty and compact. The characterizations of P(X3)
and P(X4) are given in terms of Souslin and co-Souslin sets. |
|
| Mikhail Shubin (Northeastern University) | Wednesday 3rd August 15:50 |
| Can one see the fundamental frequency of a drum? |
(Joint work with Vladimir Maz'ya)
In 1966 Marc Kac asked the famous question ``Can one hear the shape of a drum?",
formulating a goal to determine the shape of a domain in Rn by its frequencies, or,
equivalently, the eigenvalues of the Laplacian with the Dirichlet boundary conditions in this domain.
This question stimulated thousands of papers in inverse spectral problems,
which have numerous applications. The question in the title of this talk is somewhat opposite
but seems very important too. The fundamental frequency of a domain
corespponds to the lowest eigenvalue of the Dirichlet Laplacian in this domain.
The goal is to find visual characteristics of the domain which determine or at least estimate
the lowest eigenvalue. I will explain two-sided estimates for this eigenvalue in terms
of a geometric characteristic of the domain which is defined with the help of the Wiener capacity.
The results are joint work by V.Maz'ya and M.Shubin. They are closely
related to a recent solution of a problem which was
formulated by I.M.Gelfand in 1953 and solved in a recent paper by these authors
(to appear in Annals of Mathematics). |
|
| Valery Smyshlyaev (University of Bath) | Tuesday 9th August 17:10 |
| Spectral problems for high contrast periodic media and homogenisation |
| Bands and gaps in the Bloch spectrum of an elliptic
operator with highly contrasting coefficients can be described
asymptotically explicitly (e.g. Hempel & Lienau; Zhikov). For
"large defects" in such media (a problem related to wave localisation
in photonic crystal fibres) we find an asymptotically complete set of
eigenvalues and eigenfunctions inside the gap and prove the error
bounds, using two-scale asymptotic analysis supplemented by high
contrast homogenisation methods recently developed by V.V. Zhikov. We
finally discuss a problem of resonances near the real axis in "finitely
periodic" media with defects. Joint work with I.V. Kamotski. |
|
| Zeev Sobol (Swansea) | Monday 8th August 17:10 |
| Dirichlet spaces with no reference measure. |
| Nowdays Dirichlet form theory, started by Beurling and Deny and developed by Fukushima, heavily relyes on the L2
space of a reference measure. As shown by Fukushima, a change of the
measure corresponds to a random time change of the process. Hence the
attempt to develop a Dirichlet forms theory independent of the
reference measure, and its counterpart - Markov processes theory
independent of time change. Among the results, transience and
reccurence, reducibility and explosion are shown independent of the
measure choice. |
|
| Michail Solomyak (Weizmann Institute) | Friday 5th August 09:20 |
| On the spectrum in Smilansky's model of irreversible quantum graphs |
| In the model suggested by Smilansky one studies the
interaction between a quantum graph and a system of one-dimensional
harmonic oscillators attached at different points in the graph.
Mathematically, the problem reduces to study of
a family of partial differential operators, depending on several real
parameters
whose number is equal to the number of the oscillators attached. All
these operators are defined by the same differential equation but
different boundary conditions, of transmission type. Each condition
involves a real parameter
The family exhibits some interesting properties, including the phase transition at special values of the parameters.
In the talk I suppose to describe the basic results for
the leading case of one oscillator attached. Part of the results was
obtained in cooperation with S.N.Naboko. Some results for several
oscillators, obtained in cooperation with W.D.Evans, will be reported
in his talk. |
|
| Toshikazu Sunada (Meiji University) | Wednesday 3rd August 09:20 |
| Geometric theory of lattice vibrations |
| This talk discusses, from a geometric standpoint, a
classical subject in the solid state physics which dates back to
Einstein's pioneering work in 1907 and its refinement by Debye in 1912
on the specific heat of a solid. The idea and method are taken up from
discrete geometric analysis which has been recently developed for the
spectral geometry of crystal lattices. This is the joint work with M.
Shubin. |
|
| Peter Topalov (Universität Zürich) | Wednesday 3rd August 10:50 |
| An inverse spectral result for a class of integrable billiard tables |
(Joint work with Georgy Popov)
We consider a class of Riemannian manifolds with boundary having integrable
geodesic flows and solve an inverse spectral problem involving the
reconstruction of a smooth function defined on the boundary from
the spectrum of the Laplace-Beltrami operator with Robin boundary conditions. |
|
| Francoise Truc (Université Joseph Fourier) | Monday 8th August 17:40 |
| Accuracy on eigenvalues for Schrödinger Operator with a degenerate potential
in the semi-classical limit |
(Joint work with Abderemane Morame, Université de Nantes, France)
We consider a semi-classical Schrödinger operator -h^2 Delta + V with a
degenerate potential V(x,y)=f(x)g(y); g is assumed to be a homogeneous
positive
function of m variables , smooth outside 0, and f is a smooth and
strictly positive function of n variables with a strict convex minimum
.
In the case where f tends to infinity to infinity, the potential
is still degenerate in the sense that it does not go to infinity at
infinity; but the operator has compact resolvent and we give the
asymptotic behaviour, for small values of the parameter h, of the
number of eigenvalues less than a fixed energy.
Without assumption on the limit of f, we give a sharp
asymptotic behaviour of low eigenvalues bounded by some power of the
parameter h, by improving Born-Oppenheimer approximation. |
|
| Nikolai Vasilevski (CINVESTAV) | Tuesday 9th August 15:50 |
| Commutative algebras of Toeplitz operators and Berezin quantization |
| We give a complete description of commutative C*-algebras of
Toeplitz operators in terms of pencils of hyperbolic geodesics on
the unit disk.
We discuss as well the spectral behaviour of Toeplitz operators
when the wight parameter of the Bergman space varies. |
|
| Juan Weisz (Instituto de Desarollo Tecnologica para la Industria Química) | Poster |
| Systems of Commutating Matrices |
|
|
| Dimitri Yafaev (Université de Rennes 1) | Thursday 11th August 15:50 |
| A particle in an inhomogeneous magnetic field. |
| Classical and quantum equations of motion in the magnetic field of an infinite straight wire are explicitly solved. |
|
| Boguslaw Zegarlinski (Imperial College London) | Wednesday 10th August 10:50 |
| Coercive inequalities and nonlinear parabolic problems in infinite dimensions |
| We will present results on existence, uniqueness,
hypercontractivity and ergodicity of nonlinear semigroups on infinite
dimensional spaces in situations where coercive inequalities of
Log-Sobolev type are available. |

