| Sumiyoshi Abe (University of Tsukuba) | Thursday 6th July 16:50 |
| Thermodynamics based on time average and temporal extensivity of entropy |
| The recently proposed time-average approach to thermodynamics is reexamined and generalized to nonextensive thermostatistics. It is shown that the Tsallis entropy is temporally extensive: its production rate is constant, whenever it is physically relevant. The universal upper bound is derived for the Tsallis entropy production rate. |
|
| Peter Ashwin (University of Exeter) | Thursday 6th July 11:25 |
| Dynamical systems with nonergodic properties |
| This talk will discuss a number of examples, mostly from symmetric dynamical systems, where attractors may be robust and non-ergodic. As a consequence the statistical behaviour of attractors in these systems can be very fragile on addition of noise-like perturbations. |
|
| Claude Baesens (University of Warwick) | Thursday 6th July 09:50 |
| Discommensuration theory and shadowing in Frenkel-Kontorova models |
| The Frenkel-Kontorova model is a chain of balls and springs in a spatially periodic potential and is relevant to model, for instance, spatially modulated structures in solid-state physics. Equilibrium states of such models are in one to one correspondence with the orbits of some area-preserving twist maps, with ground states described by the Aubry-Mather theory and, in this context, equivalence was established between the notions of uniform hyperbolicity for the orbits and phonon gap for the equilibrium points (*).
According to "discommensuration theory" introduced by physicists, an incommensurate ground state, (i.e. with irrational mean spacing) can be seen as an "array of discommensurations" on a commensurate ground state of nearby rational mean spacing. Using continuous shadowing for uniformly hyperbolic dynamical systems we put this discommensuration theory on a rigorous footing for Frenkel-Kontorova models by proving the following result: if the minimum energy advancing discommensuration of mean spacing p/q is unique up to translation and has phonon gap then all minimum energy states with mean spacing w just above p/q are approximated exponentially well in qw-p by a concatenation of segments of advancing discommensurations.
References:
(*) S. Aubry, R.S. MacKay and C. Baesens, Equivalence of
uniform hyperbolicity for symplectic twist maps and phonon gap for
Frenkel-Kontorova models, Physica D 56 (1992) 123-134.
C. Baesens and R.S. MacKay, Discommensuration theory and shadowing in Frenkel-Kontorova models, Physica D 216 (2006) 179-184. |
|
| Oscar Bandtlow (University of Nottingham) | Tuesday 11th July 18:00 |
| Explicit bounds for the correlation specrum of real analytic
expanding maps |
(Joint work with Oliver Jenkinson)
Given a real analytic expanding map T the correlation
spectrum, that is, the set of possible exponential decay-rates of
the time correlation functions corresponding to smooth observables, is
known to be a discrete set {λn} with
λn→0. In this talk
I will discuss a method that yields simple, explicitly computable upper
bounds for each λn expressible in terms of
mapping properties of the inverse branches of T. |
|
| Christian Beck (Queen Mary, University of London) | Saturday 8th July 16:50 |
| Statistical mechanics of nonhyperbolic coupled map lattices |
(Joint work with S. Groote)
I will present some new perturbative results for the invariant 1-point density
of coupled map lattices consisting of weakly coupled Tchebyscheff maps of
N-th order. We show that typical expectations of
observables scale with the square root of the coupling constant, and that there
are log-periodic oscillations of the invariant density both in parameter and
phase space. I will explain why these types of lattice dynamical systems are
of relevance for stochastically quantized field theories and cosmology. |
|
| David Broomhead (University of Manchester) | Wednesday 12th July 10:50 |
| Iterated function systems and randomly forced PDEs |
(Joint work with J.P. Huke, James Montaldi and M.R. Muldoon)
The basic model studied here is the cable equation - a linear PDE which is used to study the dynamics of an extended conductor with uniform resistance and uniform capacitive and leakage coupling to an earthed environment. This model has been much used in modelling passive conduction in, for example, neuron dendritic trees. Here we consider the response of such a system to random, clocked digital pulses. We show that the system has a finite-dimensional attractor and show how to compute its Hausdorff dimension. It is interesting to compare the behaviour of this system for two extremes models of the physical domain: a simple 1D conductor of finite length; and the Sierpinski gasket. |
|
| Henk Bruin (University of Surrey) | Tuesday 4th July 09:50 |
| Equilibrium states and Young tower constructions in
one-dimensional dynamics
|
Young towers are being used for an increasing number of
applications; recently for the construction of equilibrium states for
specific potential functions.
Equilibrium states are invariant measures that maximize a certain
functional involving the potential function and entropy.
However, when using a a Young tower construction, the resulting
equilibrium state may only be unique and maximal within the class of
measures that can be lifted to this specific Young tower. A priori, a
different Young tower may result in different equilibrium states.
In this talk I want to restrict attention to smooth maps on the
interval and discuss a canonical way of constructing Young towers using
the Hofbauer tower. I will show that, within the class of invariant
measures with positive Lyapunov exponent, equilibrium states are indeed
independent of the choice of the Young tower. |
|
| Leonid Bunimovich (Georgia Tech) | Saturday 8th July 09:00 |
| Escape from a circle and Riemann hypotheses
|
(Joint work with C.Dettmann)
A comparison of escape rates in open systems with one and with many "holes" may provide an interesting information about dynamics of the corresponding close systems. It seems to be a quite challenging problem though, as, seemingly the simplest problem of this type, a comparison of escape rates from a circular billiard with one and with two holes, turned out to be equivalent to the Riemann hypotheses. |
|
| Hugues Chaté (CEA - Saclay) | Saturday 8th July 17:25 |
| Low-dimensional chaos in populations of strongly-coupled noisy nonlinear maps |
| We characterize the macroscopic attractor of infinite populations of noisy maps subjected to global and strong coupling by using an expansion in order
parameters. We show that for any noise amplitude there exists a large region of strong coupling where the macroscopic dynamics exhibits low-dimensional
chaos embedded in a hierarchically-organized, folded, infinite-dimensional
attractor. Both this structure and the dynamics occurring on it are well-captured by our expansion. In particular, even low-degree approximations
allow to calculate efficiently the first Lyapunov exponents of the
full system. |
|
| Eddie Cohen (Rockefeller University) | Friday 7th July 09:00 |
| Stationary states and fluctuations |
| A Survey is given of some properties of Stationary States in Equilibrium, Near Equilibriuum and Far from Equilibrium and their Fluctuations. |
|
| Maurice Courbage (Paris) | Monday 10th July 11:25 |
| Computation of entropy increase for Lorentz gas and hard disks |
| Entropy functionals are computed for non-stationary distributions of particles of
Lorentz gas and hard disks. The distributions consisting of beams of particles are found to have the largest amount of entropy and entropy increase. The computations show exponentially monotonic increase during initial time of rapid approach to equilibrium. The rate of entropy increase is bounded by sums of positive Lyapounov exponents. |
|
| Predrag Cvitanovic (Georgia Tech) | Wednesday 12th July 09:00 |
| Exact recurrent structures in shear flow turbulence |
| Experimental and computational studies point to the existence and
importance of coherent structures. Recent full Navier-Stokes computations
of unstable traveling waves in plane Couette, Poiseuille, and pipe flows
captures remarkably well qualitatively and quantitatively the turbulent
structures observed in great detail in several 3-d PVI experiments.
However, turbulence itself does not occur on the steady solutions, but on
nearby ergodic attractors. We test the "recurrent coherrent states''
description of turbulence on a Kuramoto-Sivashinsky model, as well as on full Navier-Stokes plane Couette flow, deploying a new variational method that yields a large number of numerical unstable spatiotemporally periodic solutions.
For a small but turbulent system, the attracting set appears surprisingly thin. Its backbone are several Smale horseshoe repellers, well approximated by local return maps, each with good symbolic dynamics. |
|
| Ruslan Davidchack (University of Leicester) | Wednesday 12th July 09:50 |
| Locating periodic orbits in high-dimensional systems by stabilising transformations |
| An algorithm for detecting unstable periodic orbits (UPO's) based on stabilising
transformations has had considerable success in low dimensional chaotic systems [1]. Applying the same ideas in higher dimensions is not trivial due to a rapidly increasing number of required transformations. We have proposed a much smaller set of transformations based on the stability properties of the UPO's and successfully applied it to systems with dimension up to six [2]. In this talk I will present our attempt to extend this approach to high dimensional flows such as discretised PDE's. In particular, I will report the results of using the stabilising transformations to locate periodic and relative periodic orbits in the Kuramoto-Sivashinsky system.
[1] R. L. Davidchack and Y.-C. Lai, Efficient algorithm for detecting unstable periodic orbits in chaotic systems. Phys. Rev. E 60, 6172-6175 (1999).
[2] J. J. Crofts and R. L. Davidchack, Efficient detection of periodic orbits in chaotic systems by stabilizing transformations. SIAM J. Sci. Comput., to appear. |
|
| Carl Dettmann (University of Bristol) | Saturday 8th July 09:50 |
| Escape rates and correlation functions |
(Joint work with L. A. Bunimovich)
We consider classical chaotic billiards with holes in the boundary, and define as usual the (exponential) escape rate from the long time decay of a measure initially invariant with respect to the corresponding closed system (ie without holes). Experimentally it is feasible to measure the escape rate as a function of the size and location of the hole(s), and hence discover properties of the closed dynamical system. We expand the escape rate in powers of the size of the hole. At the first order it is the size of the hole (relative to the boundary) divided by the mean time between collisions. Further corrections involve sums of correlation functions. Numerically, we confirm the results using a diamond billiard formed by four concave circular arcs. |
|
| John Elgin (Imperial College, London) | Tuesday 4th July 12:00 |
| Pointwise dimensions of the Lorenz attractor |
| We discuss a connection between two complementary views of the lorenz attractor: the first is the accepted view where the attractor has a smooth measure on a fractal support. This complex system is alternatively manifest as a self-similar curve for the pointwise dimension 'alpha'. We describe why the latter approach is accessible for the analysis of an experimental signal. |
|
| Denis Evans (Australian National University) | Friday 7th July 10:50 |
| The fluctuation & nonequilibrium free energy theorems, theory & experiment |
(Joint work with Edie Sevick, Genmaio Wang, David Carberry and James Reid
Research School of Chemistry, Australian National University, ACT, Australia
and
Debra J. Searles
Griffith University, QLD, Australia)
We give a brief summary of the derivations of the Evans-Searles Fluctuation Theorems (FTs) and the NonEquilibrium Free Energy Theorems (Crooks and Jarzynski). The discussion is given for time reversible Newtonian dynamics. We emphasize the role played by thermostatting. We also highlight the common themes inherent in the Fluctuation and Free Energy Theorems. We discuss a number of simple consequences of the Fluctuation Theorems including the Second Law Inequality, the Kawasaki Identity and the fact that the dissipation function which is the subject of the FT, is a nonlinear generalization of the spontaneous entropy production, that is so central to linear irreversible thermodyanamics.
Lastly we give a brief update on the latest experimental tests of the FTs (both steady state and transient) and the NonEquilibrium Free Energy Theorem, using optical tweezer apparatus.
|
|
| Mike Field (Houston) | Thursday 6th July 10:50 |
| Symmetry and dynamics |
| The presence of additional structure - such as symmetry or reversibility -
can impose strong local and global geometric constraints on dynamics.
We describe some results with applications to both local and global
dynamics. |
|
| Yan Fyodorov (University of Nottingham) | Saturday 8th July 12:00 |
| Counting stationary points of random landscapes as a random matrix problem |
Finding the mean of the total number Ntot of
stationary points for N-dimensional random Gaussian landscapes
can be reduced to averaging the absolute value of characteristic
polynomial of the corresponding Hessian. First such a reduction is
illustrated for a class of models describing energy landscapes of
elastic manifolds in random environment, and a general method of
attacking the problem analytically is suggested. Then the exact
solution to the problem [Y.V. Fyodorov, Phys. Rev. Lett. 92, 240601
(2004); ibid 93, 149901(E) ( 2004)] for a class of landscapes
corresponding to the simplest, yet nontrivial toy model with N
degrees of freedom is described. For N >> 1 our asymptotic
analysis reveals a phase transition at some critical value
μc of a control parameter μ. Namely, for μ <
μc the landscape is characterized by finite landscape
complexity Σ > 0, corresponding to exponentially many stationary
points: Ntot~exp(N Σ).
In contrast, for μ > μc the complexity vanishes in
the thermodynamic limit N>>1: Σ=lim
ln(Ntot)/N=0.
This is interpreted as a transition to a glass-like state of the matter
for μ<μc.
|
|
| Giovanni Gallavotti (Universitŕ degli Studi di Roma ) | Tuesday 4th July 16:00 |
| Chaotic hypothesis and some consequences |
| The chaotic hypothesis is proposed as a basis for a general theory of
nonequilibrium stationary states. |
|
| Pierre Gaspard (Université Libre de Bruxelles) | Tuesday 4th July 11:25 |
| Pollicott-Ruelle resonances, fractals, and nonequilibrium modes of relaxation |
|
|
| Paul Glendinning (University of Manchester) | Tuesday 11th July 16:50 |
| Sensitive dependence and strange nonchaotic attractors |
| I will describe some recent work with Tobias Jaeger and Gerhard Keller on the chaotic properties of strange nonchaotic attractors |
|
| Mark Holland (University of Exeter) | Tuesday 11th July 11:25 |
| Limit theorems and rapid mixing for Lorenz attractors |
| We prove statistical limit theorems (for example the CLT) for Holder observations of the Lorenz attractor, and more generally for geometric Lorenz attractors.
In work in progress, it is expected also that the Lorenz attractor is rapid mixing
(for a positive measure set of parametrized Lorenz attractors).
|
|
| Teil Howard (University of Bristol) | Poster |
| Asymptotic expansions for the escape rate of stochastically perturbed dynamical systems |
(Joint work with C.P. Dettmann)
Deterministic differential equations governing physical systems are idealised and in reality will be affected by noise at some scale. This motivates the study of systems which evolve with noise, specifically maps with additive noise.
The escape rate of a system can easily be calculated from the leading eigenvalue of the Fokker-Planck evolution operator. In the case of noisy maps this eigenvalue can be calculated as an expansion in terms of the noise strength by finding the roots of the spectral determinant. In order to calculate these, traces of powers of the evolution operator must first be obtained.
Different approaches may be taken to calculate the traces such as Feynman diagrams and smooth conjugations however these methods can only calculate the expansion to the fourth order in noise strength. The highest orders can be achieved numerically by using a local matrix representation of the evolution operator. When combined with high precision arithmetic this method can obtain results up to order 64 in the noise strength.
With such a high order expansion obtained to a high degree of accuracy it is possible to look at the asymptotic form of the late terms with a combination of analysis and curve fitting. This involves finding the singulant by calculating the probability of returning to the repeller and finding a real parameter alpha. A variety of different systems are studied to verify the analysis used to find the asymptotic form since previous work has focused on one specific system. These systems are also used to try to find the significance of alpha, particularly whether it is related to the fractal dimension of the repeller. In the system studied previously a tentative connection was proposed to the Renyi generalised dimension D∞ but new data has shown that this is probably not the case.
|
|
| Oliver Jenkinson (Queen Mary, University of London) | Tuesday 11th July 17:25 |
| How "spread out" are invariant measures? |
Fix a dynamical system.
Given two periodic orbits (or more generally two invariant probability measures), is there a way of saying that one is more "spread out" than the other?
I will describe a partial order on the set of invariant probability measures which does just this, and identify the minimal (least spread out) and maximal (most spread out) measures for this ordering.
These results will then be interpreted in terms of ergodic optimization
(i.e. invariant measures with smallest/largest ergodic average). |
|
| Thomas Jordan (University of Warwick) | Poster |
| Self-affine sets with random pertubations |
(Joint work with Mark Pollicott and Karoly Simon)
We consider iterated function systems consisting of a finite number of contracting affine maps. An upper bound for the Hausdorff dimension of the attractor can be found based on the singular values of the maps. When the matrix norms are 1/2 Falconer has shown that for a 'large' set of systems this value is indeed the Hausdorff dimension of the attractor. We add a random translation at each stage to the iterated function system. For certain distributions we show that almost surely the Hausdorff dimension of the attractor is as expected. For this case the only assumption used is that the norms of the affine maps are less than 1. |
|
| Wolfram Just (Queen Mary, University of London) | Saturday 8th July 18:00 |
| On critical behaviour of coupled map lattices |
| Piecewise linear coupled Markov maps are analysed in terms of
probabilistic cellular automata. Phase transitions in
these dynamical systems are investigated.
Critical exponents of particular coupled map lattices
and their associated probabilistic cellular
automata are determined using finite size scaling procedures.
Ising universality is found for reversible probabilistic cellular
automata in accordance with analytical predictions. When detailed
balance is violated deviations from Ising universality may occur.
Critical exponents of a variant of the Miller Huse model and of a coupled
map lattice related with Toom probabilistic cellular automata are
evaluated. |
|
| Michael Kastner (Universität Bayreuth) | Monday 10th July 17:25 |
| Phase transitions and configuration space topology |
| Two mechanisms, responsible for the generation of a thermodynamic singularity, are discussed. For a class of short-range, confining potentials, a topology change in some family of configuration space submanifolds is the only possible such mechanism. Two examples of systems in which the phase transition is not accompanied by such a topology change are presented. The first one is a model with long-range interactions, namely the mean-field φ4-model, the second example is a one-dimensional system with a non-confining potential energy function. For both these systems, the thermodynamic singularity is generated by a maximization over one variable (or one discrete index) of a smooth function, although the context in which the maximization occurs is very different.
|
|
| Gerhard Keller (Universität Erlangen) | Saturday 8th July 16:00 |
| Absence and existence of phase transitions in piecewise expanding coupled map lattices |
I will report about two results on weakly coupled Zd
lattices of piecewise expanding interval maps.
The first result is joint
work with Carlangelo Liverani (Rome) [CMPh 262 (2006) 33-50]. It can be
summarized, a bit loosely, as follows: For each "sufficiently weak" and
"regular" coupling of finite range, the dynamical system has a unique
invariant measure in a "suitable" space of measures with absolutely continuous
finite-dimensional conditional maginals. This measure is exponentially mixing
both in time and in space, and it is "the SRB" measure of the system. The proof
relies on the observation that the system's transfer operator
has a spectral gap as an operator on (an extension of) this "suitable"
space of measures.
The second result, joint work with Jean-Baptiste Bardet (Rennes),
complements this in the following way: we construct a continuous piecewise
linear and expanding interval map which, when coupled diffusively to its
nearest "north" and "east" neighbours on Z2, displays a phase
transition. In particular, for suitable coupling strength, it has at least two
invariant measures in the aforementioned "suitable" class of measures while for
the same coupling strength all finite lattice versions of this system have a
unique absolutely continuous invariant measure. The proof relates the dynamics
of the system to those of Toom's probabilistic cellular automaton.
|
|
| Kostya Khanin (University of Toronto) | Tuesday 4th July 16:50 |
| Circle dynamics and rigidity |
| We present two recent results related to rigidity theory in circle dynamics.
The first one is related to a phenomenon of robust rigidity for circle
diffeomorphisms with singularities. We prove (jointly with Alexey Teplinsky)
that two analytic critical circle maps with the same order of the critical
points and the same irrational rotation number are C1-smoothly conjugated
to each other. It is important that the result holds for all irrational numbers
without any Diophantine-type conditions.
The second result (joint with Bassam Fayad)solves the problem formulated by J.Moser about 15 years ago. We prove that commuting circle diffeomorphisms can be smoothly (and simultaneously) linearized provided that
their rotation numbers satisfy the joint Diophantine condition. |
|
| Ramaz Khomeriki (Florence University) | Poster |
| Long-range effects in layered spin structures |
| The layered spin structures are studied theoretically with the aim of predicting realistic testable effects of long range dipolar interactions. As shown dipolar interaction between the spin layers open gaps in allowable energy versus magnetization phase diagram. The consequences of this behavior, particularly, the bifurcation of the system state under application of external magnetic field and the ways of possible experimental verification are pointed out. |
|
| Rainer Klages (Queen Mary, University of London) | Tuesday 11th July 09:50 |
| Anomalous diffusion in intermittent maps |
(Joint work with N.Korabel, A.V.Chechkin, I.M.Sokolov and V.Yu.Gonchar)
Nonlinear intermittent maps provide an interesting playground in order
to study anomalous transport both as stochastic processes and in terms of
dynamical systems theory. For a simple map lifted subdiffusively onto
the real line computer simulations indicate that the generalized
diffusion coefficient is a fractal, discontinuous function of control
parameters. An amended continuous time random walk theory
continuously approximates its coarse functional form and reproduces a
phase transition-like suppression of the strength of
diffusion. Similarly, the probability density of this model exhibits a
nontrivial fine structure related to the invariant density of the map
on the unit interval while the coarse functional form is governed by a
time fractional diffusion equation.
References: N.Korabel et al., Europhys. Lett. 70, 63 (2005) |
|
| Peter Kleban (University of Maine) | Tuesday 4th July 17:25 |
| The Farey fraction spin chain |
| The Farey Fraction Spin Chain is a set of one-dimensional statistical mechanical models built on the Farey fractions (modified Farey sequence). These models lie between statistical mechanics and number theory, and are of interest in both areas. A direct connection to dynamical systems is used to prove that the models rigorously exhibit a (barely) second-order phase transition. Additionally, one may calculate certain correlation functions. The phase diagram, including an external magnetic field, is determined by means of renormalization group and also via a (dynamical system inspired) cluster approximation. The results, interestingly, are almost consistent. Examination of the partition function at the critical point suggests a subtle, apparently new, property of the Farey fractions. There are also rigorous results by number theorists for the “density of states” and a close connection to the Lewis three-term equation, extensively studied in the theory of the Selberg zeta-function.
|
|
| Robert MacKay (University of Warwick) | Wednesday 5th July 09:00 |
| From Hamiltonian slow-fast systems to Langevin equations |
| I will sketch a derivation of a Langevin equation for the slow degrees of freedom in a Hamiltonian system whose other degrees of freedom are fast and Anosov. The key steps are Ruelle's SRB measure for non-autonomous systems and martingale theory. |
|
| Spyros Martzoukos (Queen Mary, University of London) | Poster |
| Deterministic walks on infinite planar graphs |
(Joint work with T. Prellberg)
We consider Lorentz lattice gas
cellular automata on infinite planar graphs, in particular Delaunay
triangulations of an infinite set of points in the plane. We present an
algorithm on how to generate a deterministic walk (i.e. a walk in the
presence of scattering rules) on such a graph, and focus on whether all
trajectories eventually close. |
|
| Dieter Mayer (TU Clausthal-Zellerfeld) | Friday 7th July 18:00 |
| The transfer operator approach to quantum chaos on modular surfaces |
The generalized transfer operator Lβ plays an important role in the ergodic theory of classical dynamical systems. For the geodesic flow on certain surfaces of constant negative curvature like the modular surfaces this operator can be used to connect the classical properties of these systems to their quantum properties: the so called non-trivial zeros of its Fredholm determinant
det(1−Lβ) determine both the energy eigenvalues and the resonances of these systems. Furthermore can the corresponding eigenfunctions of Lβ be directly related through an explicit integral transformation to the bound states respectively the scattering states of the quantum system. As is well known these quantum systems possess an infinite family of internal symmetries described by the so called Hecke operators. There exists an analogous family of commuting operators also in the spaces of eigenfunctions of the classical transfer operator Lβ.
It turns out that these classical eigenfunctions of Lβ are rather interesting objects also in number theory: they are closely related to the so called period functions attached to automorphic functions. |
|
| Peter McClintock (Lancaster University) | Wednesday 5th July 16:00 |
| Experiments on large fluctuations and optimal control |
(Joint work with I.A. Khovanov and D.G. Luchinsky)
Most
of the interesting and important events in fluctuating systems
involve large fluctuations. Examples include chemical reactions,
mutations in DNA sequences, failures of electronic devices and
lasers, stochastic resonance, and protein transport in Brownian
ratchets. Although rare, when they arise, large fluctuations occur
in an almost deterministic way, following optimal fluctuational
paths that minimise an effective activation energy. The subject
has a long history. The concept of large fluctuations was
originally introduced by Boltzmann, and the theory was
subsequently developed by many other scientists and
mathematicians. In the weak noise limit, the Fokker-Planck
equation can be solved by the Eikonal approximation, leading to a
Hamiltonian auxiliary system. Its (deterministic) minimum-action
trajectories correspond to the optimal paths of the real physical
system.
Analogue electronic experiments and numerical simulations have
been used to reveal the optimal paths and to identify the physical
significance of the optimal force [1,2]. The same experimental
approach can be applied to find the energy-optimal force required
to induce escape from a chaotic attractor [3], even in cases where
the basin boundaries are fractal [4]. It can also be applied to
find the energy-optimal control function for e.g. effecting
migration of a class-B laser from its stable limit cycle to a
saddle cycle, allowing a direct comparison of the efficiency of
pulsed and continuous control, and showing that continuous control
is the more energy-efficient [5].
The talk will introduce the idea of optimal paths and will
show how the experiments and simulations have assisted in the
development of the theory and its physical interpretation.
-
D.G. Luchinsky and P.V.E. McClintock, "Irreversibility of
classical fluctuations studied in electrical circuits", Nature
389, 463-466 (1997).
-
D.G. Luchinsky, P.V.E. McClintock and M.I. Dykman, "Analogue
studies of nonlinear systems", Rep. Prog. Phys. 61, 889-997
(1998).
-
I.A. Khovanov, D.G. Luchinsky, R. Mannella and P.V.E.
McClintock, "Fluctuations and the energy-optimal control of
chaos", Phys. Rev. Lett. 85, 2100-2103 (2000).
-
A.N. Silchenko, S. Beri, D.G. Luchinsky and P.V.E. McClintock,
"Fluctuational transitions through a fractal basin boundary",
Phys. Rev. Lett. 91, 174104 (2003).
-
I.A. Khovanov, N.A. Khovanova, E.V. Grigorieva, D.G. Luchinsky
and P.V.E. McClintock, "Dynamical control: comparison of map and
continuous flow approaches", Phys. Rev. Lett. 96, 083903 (2006).
|
|
| Ian Melbourne (University of Surrey) | Monday 10th July 10:50 |
| Almost sure planar diffusive behaviour in the planar periodic Lorentz
gas |
(Joint work with Matthew Nicol)
Consider a planar periodic Lorentz gas with finite horizon. Bunimovich
and Sinai (1981) proved that the position vector q(t) satisfies a
two-dimensional central limit theorem. They also proved its functional
version (weak invariance principle): convergence in distribution to a
two-dimensional Brownian motion.
In this talk, we describe the almost sure invariance principle (ASIP):
for almost any initial condition, q(t) is approximately a
two-dimensional Brownian trajectory. This answers a question of
Chernov and Dolgopyat.
More generally, we prove a vector-valued ASIP for Axiom~A
diffeomorphisms and flows as well as large classes of nonuniformly
hyperbolic systems.
|
|
| Tania Monteiro (University College London) | Saturday 8th July 10:50 |
| Chaotic diffusion and cold atoms |
Experiments with cold atoms in pulsed standing waves of light provide a
very clean realisation of the Quantum Kicked Rotor (QKR); the corresponding
classical behaviour is given by the Standard Map, a leading paradigm
of Hamiltonian chaos. Experiments by half a dozen cold-atom groups
world-wide have, since 1995, demonstrated a range of effects such as:
quantum suppression of diffusion (dynamical localization);
chaos assisted quantum tunnelling between stable islands; accelerator
modes.
Here, two recent developments will be reported:
(1) Experiments using pairs of closely spaced pulses indicate a
profound modification of the classical diffusive process; phase-space has a
cellular structure, with fast diffusion regions separated by thin
slow-diffusing regions. Quantum states then experience a delocalization
transition from one 'cell' to many: at this point exponential
localization lengths scale as
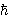 .75, not as .75, not as 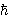 -1
as in the ordinary QKR (Creffield, Hur and TM, Phys Rev Lett
(96)024103 (2006)). This scaling is not yet understood. -1
as in the ordinary QKR (Creffield, Hur and TM, Phys Rev Lett
(96)024103 (2006)). This scaling is not yet understood.
(2) Chains of atoms with spin 1/2 (Heisenberg spin chain) with a
single spin-excitation have been the subject of much interest in
quantum information/quantum computing. For such a chain in a pulsed
magnetic field, a formal correspondence between its time-evolution operator
and that of the QKR is shown. This implies that all
the phenomena driven by the classical diffusion (including all correlations)
of the QKR have an 'image' in the spin chain: for example diffusion
in position-space for the QKR corresponds to diffusion through
a Hilbert subspace of eigenstates the spin-chain etc. Using this, one can
analyse entanglement measures and quantum-state transmission
(Boness,Bose,TM, Phys.Rev.Lett. to appear May 2006).
|
|
| Gary Morriss (University of New South Wales, Sydney) | Tuesday 11th July 09:00 |
| Lyapunov vectors and modes |
| Dynamical instability is characterized by the Lyapunov exponents
which give the rate of separation of nearby trajectories. In general,
there is one exponent for each independent direction in phase space.
While for many exponents the direction of separation varies rapidly,
for some exponents the direction is either fixed or slowly varying.
We call these fixed or slowly varying directions the Lyapunov modes.
Here we show that the frequency of the slowest time variation of the
Lyapunov modes is connected with the oscillation frequency of the
tail of the velocity autocorrelation function, an experimentally
measurable quantity.
[Figure]
The figure shows the time and spatial variation of one of the key
Lyapunov modes for a quasi-one-dimensional system of hard disks. The
form of the Lyapunov mode is connected to the invariant properties of
the system. The importance of this phenomenon is that it connects
stability properties and macroscopic collective movement (phonons) in
a many-body system.
We discuss simple models that describe the localization of Lyapunov
vectors and the dynamics of the localized region at low density. We
present the Lyapunov modes for a non-equilibrium particle system. |
|
| Vincent Naudot (University of Warwick) | Poster |
| Analytic invariants associated
with a parabolic fixed point in C2 |
| Near a parabolic fixed point on the plan, a real analytic
diffeomorphism can be embedded in a smooth autonomous
flow. We show that in the complex-analytic situation is
completely different.
We construct two analytic invariants with respect to local analytic
changes of coordinates.
This invariant vanishes for time-1 maps of analytic flows but
generically different from 0.
|
|
| Yakov Pesin (Pennsylvania State University) | Tuesday 4th July 09:00 |
| Thermodynamics of systems admitting Young's tower |
| I will describe thermodynamical formalism for dynamical systems with nonzero Lyapunov exponents admitting Young's tower. This includes constructing equilibrium measures corresponding to a certain class of potential functions and to a certain space of invariant measures as well as studying uniqueness of equilibrium measures and describing their ergodic properties.
|
|
| Alessandro Pluchino (Universitŕ di Catania) | Wednesday 5th July 17:25 |
| The role of synchronization for detecting community structures in complex networks |
| Community structures are an important feature of many social, biological and technological networks. We explore the role of synchronization for detecting communities in complex networks of identical oscillators coupled with weighted links. |
|
| Harald Posch (University of Vienna) | Tuesday 11th July 16:00 |
| Phase-space instability for particle systems in equilibrium
and stationary nonequilibrium states
|
| Exponentially-growing tangent-space perturbations associated with the
small positive Lyapunov exponents of many-particle systems
exhibit coherent stationary patterns in physical space, to which
we refer as "Lyapunov modes". They were first observed for hard-disk fluids
in one, two and three dimensions. Using refined Fourier-transformation
methods, we demonstrate that they exist also in soft-disk systems.
We discuss the symmetry properties and remark on the dynamics of the modes.
In addition, we study many-particle systems in stationary
nonequilibrium states and review some recent results on the phase-space contraction and the associated phase-space fractals. Both dynamical and stochastic thermostats are considered.
|
|
| Thomas Prellberg (Queen Mary, University of London) | Tuesday 4th July 18:00 |
| The Farey fraction spin chain: Effects of an external field |
| We consider the Farey fraction spin chain in an external field h. Using ideas from dynamical systems and an operator analysis, we rigorously compute the asymptotic expansion of the free energy f in the vicinity of the second-order phase transition point.
|
|
| Piero Quarati (Politecnico di Torino) | Wednesday 12th July 16:35 |
| Use of non-Maxwellian distributions in atomic and nuclear processes of astrophysical interest |
|
|
| Andrea Rapisarda (Universita di Catania) | Wednesday 5th July 16:50 |
| Anomalous dynamics and long range interactions |
| I will review recent findings of anomalous dynamics
in systems with long range interactions. Possible interpretations
in terms of Tsallis statistics and glassy behaviour will be also addressed. |
|
| Alberto Robledo (Universidad Nacional Autónoma de México) | Thursday 6th July 17:25 |
| The foundations of q-statistics for the transitions to chaos |
| We add to the ‘thermodynamic’ approach - originally employed by Mori
and colleagues to characterize dynamical phase transitions in
attractors of nonlinear iterated maps - to derive the
q-statistical properties of the fluctuating dynamics at the
period-doubling and quasiperiodic transitions to chaos. We find that
the occurrence of a dynamical phase transition at the onset of chaos
is associated to trajectories that connect specific regions in the
multifractal attractor. For these trajectories we obtain a
q-exponential sensitivity to initial conditions, and the value
of the ‘thermodynamic field’ q at a dynamical transition is the
same as the index q in the sensitivity. At such dynamical
transition the q-entropy Sq grows linearly
with time and with a rate equal to the generalized q-Lyapunov
coefficient. The intricate dynamics at these critical attractors
consists of an infinite family, with a hierarchical structure, of
q-phase transitions where the values of the indexes q
are determined by the universal jump discontinuities of the trajectory
scaling function.
|
|
| Lamberto Rondoni (Politecnico di Torino) | Friday 7th July 09:50 |
| Hypotheses for fluctuation relations in nonequilibrium systems |
| We review recent results on fluctuation relations for steady states of
nonequilibrium systems, and discuss the hypotheses under which such relations
can be obtained. This is expected to shed light on the requirements that a
dynamical theory of nonequilibrium systems may have to satisfy. |
|
| Stefano Ruffo (Universitŕ degli Studi di Firenz) | Monday 10th July 16:00 |
| Survey of the statistical and dynamical properties
of systems with long-range interactions |
| For systems with long-range interactions the potential decays at
large distances with a power which is smaller than space dimension.
Such systems are non-additive and the thermodynamic limit is questionable.
It leads to ensemble inequivalence and curious effects like negative specific
heat and temperature jumps.
I'll review recent advances in this field and I will show several examples.
I will discuss toy models whose analytic solution is available
by the extensive use of large deviation technique, but also more
realistic models, that cannot be exactly solved, but can be analysed
by numerical techniques and approximations. I will finish by discussing
in some detail the example of wave-particle interactions
(free electron lasers).
|
|
| Hans-Henrik Rugh (Université de Cergy-Pontoise) | Friday 7th July 17:25 |
| Cones and gauges in complex spaces:
Detecting spectral gaps.
|
| We introduce complex cones and their associated projective gauges,
generalizing a real Birkhoff cone and its Hilbert metric to
complex vector spaces. We deduce a variety of
complex spectral gap theorems. |
|
| David P. Sanders (Universidad Nacional Autónoma de México) | Monday 10th July 09:50 |
| Occurrence of normal and anomalous diffusion in polygonal billiard channels |
(Joint work with Hernán Larralde)
We present results [1] on the diffusive properties of polygonal billiard models: non-interacting particles bounce within periodic quasi-one-dimensional channels having polygonal boundaries and irrational angles. Such models are not chaotic in the usual sense, having
a zero Lyapunov exponent.
Surprisingly, as in the standard Lorentz gas (which has circular scatterers and is strongly chaotic) we find normal diffusion,
i.e. a mean squared displacement growing linearly in time.
The exception to this is when the unit cell contains accessible parallel scatterers. In this case, we instead find anomalous super-diffusion, i.e. power-law growth of the mean squared displacement with an exponent larger
than 1. The explanation for this is the existence of many families of propagating periodic orbits due to the parallel scatterers.
When a configuration with parallel scatterers is approached, there is a crossover from normal to anomalous diffusion, consistent with a simple scaling form, with the diffusion coefficient exhibiting a power-law divergence.
[1] David P. Sanders & Hernán Larralde (2006), Phys. Rev. E 73(2), 026205
|
|
| Roman Schubert (University of Bristol) | Saturday 8th July 11:25 |
| Universality in wave propagation for large times |
| We look at wave propagation on compact Riemannian manifolds, and are interested in the fate of a propagating wavepacket for large times and small wave-length. By classical geometric optics constructions for small wavelength the wavefronts are propagated along geodesics perpendicular to them. This means that for large times the ergodic properties of the geodesic flow determine what happens to a wavepacket. For manifolds of negative curvature the geodesic flow is hyperbolic and shows universal features like mixing and the validity of a central limit theorem. We discuss how these features lead to similar universal behavior for propagation of wavepackets. |
|
| Debra Searles (Griffith University, Brisbane) | Friday 7th July 11:25 |
| Fluctuation relations for systems far from equilibrium.
|
(Joint work with Stephen R. Williams and Denis J. Evans)
The behaviour of fluctuation relations at large fields has been considered from a theoretical perspective for some time, with different treatments predicting different results. However, it has been difficult to test the behaviour in this regime, as large fluctuations become less likely as the field is increased. To enable large fluctuations to be observed we have considered a small system [1]. Here we describe fluctuation relations that have been proposed for systems that are driven far from equilibrium, and compare their predictions with the results we obtain numerically from computer simulations of this small system. In order to interpret the results and compare with theoretical results, we also examine its Lyapunov spectrum at various fields. It is found that for the system considered, the form of the fluctuation relation does not change when the field is increased, even if the field is so high that the number of positive and negative Lyapunov exponents differs.
[1] S. R. Williams, D. J. Searles, and D. J. Evans, J. Chem. Phys, accepted for publication (2006).
|
|
| Richard Sharp (University of Manchester) | Friday 7th July 16:50 |
| Directions and equidistribution in homology for Anosov flows |
| We discuss the asymptotic distribution of the directions in homology of periodic orbits of Anosov flows. We obtain a limiting measure which is either a Dirac measure on a single point or is fully supported. In the latter case, we relate the
result to a more general equidistribution phenomenon. |
|
| Nikita Sidorov (University of Manchester) | Wednesday 12th July 11:25 |
| Iterated function systems with overlaps in higher dimensions |
| We present some new results concerning linear iterated function systems with overlaps in Rd. We extend one-dimensional results and show that in a general case a typical point has a continuum of addresses and in some cases this is in fact true for each point in the attractor. Relations with dynamics of multivalued maps and with maps with holes will be discussed. |
|
| Ray Streater (King's College London) | Monday 10th July 12:00 |
| Entropy production in a quantum Kac model |
Kac gave a ring model of a collection of two-state molecules, with a reversible dynamics; he showed that there is a sense in which the entropy increases in time. Maes et al. generalise this to a ring of quantum particles of spin 1/2, with a reversible dynamics. They claim to show that the von Neumann entropy is constant in time, but a modified entropy increases in the limit to an infinite ring, in a probabilistic sense.
We show that indeed the von Neumann entropy does increase, in a probabilistic sense, if we change the dynamics to an approximate one, such as given by the simplification in which only a few variables, called the `slow' ones, are measured.
|
|
| Andrew Stuart (University of Warwick) | Wednesday 5th July 10:50 |
| Derivation of homogenized coefficients from multiscale data |
| In many applications it is of interest to derive reduced dynamical models
from larger, more complex models. In some instances this programme can
be carried out analyitcally, for example in the presence of explicit scale separation. In other situations it is necessary to resort to computational
procedures to carry it out. In this talk we study the issues that arise
when the data from the large complex model have a multiscale character,
and the reduced dynamical model may be viewed as homogenized equation
compatible with this data.
We work in the framework of multiscale stochastic differential equations.
We describe the issues which arise when trying to find homogenized models
compatible with multiscale data. We establish, through theorems and numerical
experiments, methods to correctly identify homogenized models from data. |
|
| Rob Sturman (University of Bristol) | Wednesday 12th July 12:00 |
| The linked twist map approach to fluid mixing |
| Fluid mixing is a topic which spans a wide range of applications and
disciplines. In recent years the tools of topological dynamical systems
have been employed to place the subject of chaotic mixing on a
mathematical footing. However, topological methods frequently produce
results which only correspond to sets of zero volume. In this talk we
argue that the field of ergodic theory will play a crucial role in
supplying results on mixing for sets of positive measure which have a
direct impact on applications.
In particular, the linked twist maps of the now classical ergodic theory
literature are systems for which ergodicity, mixing and the Bernoulli
property can be shown for sets of full measure. We show that such
systems can be viewed as paradigm models for the design of fluid mixers.
We give examples from diverse areas, such as microfluidics, granular
flow and DNA hybridization to support this, and emphasize the key
directions in which the theory could be advanced to allow a
greater connection with applications. |
|
| Yuri Suhov (University of Cambridge) | Tuesday 11th July 10:50 |
| Hausdorff dimension of the limiting set of a hyperbolic branching diffusion |
(Joint work with M. Kelbert, University of Swansea)
We consider
a Markov branching diffusion process (BDP) on a Lobachevsky space (LS), with
a homogeneous (Laplace-Beltrami) generator but variable fission potential (FP).
In this process, each branch of the diffusion tree approaches a random (and
uniformly distributed) point of the absolute, and the whole tree generates a random set of accumulation points on the absolute. The Hausdorff dimension (HD) of this random set is a non-random constant, and we are interested in assessing its value. If the FP is a constant (a homogeneous BDP), the HD is given explicitly. The case of a variable FP requires different methods, which will be the subject of the talk. No preliminary knowledge of the LS geometry will be required. |
|
| Domokos Szász (Budapest University) | Monday 10th July 09:00 |
| The Lorentz process and random walks |
(Joint work with D. Dolgopyat and T. Varjú.)
First return and first hitting times, local times and first intersection
times are studied for planar finite horizon Lorentz processes with a
periodic configuration of scatterers. Their asymptotic behavior is
analogous to the asymptotic behavior of the same quantities for the
2-d simple symmetric random walk (cf. results of Erdös-Taylor, 1960).
Moreover, asymptotical distributions for phases in first hitting and in
first intersections of Lorentz processes are also described.
|
|
| Floris Takens (Universität Groningen) | Thursday 6th July 09:00 |
| KAM theory in the presence of monodromy |
| KAM theory proves that many invariant tori persist if a competely integrable Hamiltonian system is slightly perturbed. The available proof (Poeschel) makes heavily use of local coordinates (and trivialization of the torus bundle). This, together with the fact that they do not provide unicity of the perturbed tori makes it not obvious how to extend this theory in a satisfactory way to situations where the torus bundle is non-trivial. We shall demonstrate the problem with the example of the spherical pendulum, where the torus bundle has non-trivial monodromy. We then show how to extend the theory by proving a unicity result for the perturbed tori. |
|
| Tooru Taniguchi (Rockefeller University, New York) | Friday 7th July 12:00 |
| Onsager-Machlup theory for nonequilibrium steady states and
fluctuation theorems |
| Onsager-Machlup theory for nonequilibrium steady states and its
connection with fluctuation theorems are discussed for a dragged
Brownian particle. Using a functional integral approach, the
probability functional for a path is expressed in terms of a
Lagrangian function from which entropy production rate and
dissipation functions are introduced, and nonequilibrium
thermodynamic relations like the energy conservation law and the
second law of thermodynamics are derived. Using this Lagrangian
function we establish two nonequilibrium detailed balance relations,
which not only lead to a fluctuation theorem for work but also to one
related to energy loss by friction. We also present a simple argument
for the extended fluctuation theorem for heat in the long time limit. |
|
| Gregor Tanner (University of Nottingham) | Wednesday 12th July 16:00 |
| Quantum scaling laws in two electron atom - the role of the classical triple collision singularity |
(Joint work with Chang Woo Byun, Nark Nyul Choi, Min-Ho Lee - Kumoh University, South Korea)
As early as 1953, Gregory H Wannier suggested that the energy dependence of the double-ionisation cross section of two-electron atoms near the three-particle threshold can be related to the classical dynamics near the the triple collision singularity. The long range electron-electron correlation effects can then be taken into account by a linear stability analysis of the triple-collision dynamics giving results which have been confirmed in detail experimentally since.
Extending these ideas to energy regimes below the three-particle breakup threshold E<0 has proved to be difficult due to the predominantly chaotic nature of the classical dynamics in this energy regime. We will show in this talk that universal scaling laws based on Wannier exponents dominate the photo-ionisation cross section for single electron ionisation in the limit E→0_.
|
|
| Hugo Touchette (Queen Mary, University of London) | Monday 10th July 16:50 |
| Nonconcave entropies from generalized canonical ensembles |
| It is well known that the entropy of the microcanonical ensemble cannot be calculated as the Legendre transform of the canonical free energy when the entropy is nonconcave. To circumvent this problem, a generalization of the canonical ensemble which allows for the calculation of nonconcave entropies was recently proposed. In this talk, I will study a mean-field version of the Potts model, and show that the nonconcave entropy of this model can be obtained by using a specific instance of the generalized canonical ensemble known as the Gaussian ensemble. (Work in collaboration with Richard S. Ellis and Marius Costeniuc.) |
|
Constantino Tsallis (Santa Fe Institute/USA
and Centro Brasileiro de Pesquisas Fisicas/Brazil) | Thursday 6th July 16:00 |
| Nonextensive statistical mechanics and its nonlinear dynamical foundations |
| Boltzmann-Gibbs (BG) statistical mechanics are dynamically based on the hypothesis of exponential divergence in phase space, hence ergodicity; its variational formulation uses the standard BG entropy. These simplifying hypothesis are usually not satisfied in vast classes of complex natural, artificial, and social systems. Some of such systems appear to be tractable within the so called nonextensive statistical mechanics, a generalization of the BG theory. This extension dynamically refers to the edge of chaos, where the largest Lyapunov exponent vanishes, and uses the entropy Sq, which recovers the BG expression for q=1. An introduction to the theory will be given, with emphasis to various mathematical connections, including a possible q-generalization of the Central Limit Theory, which have been numerically (in some cases, analytically) illustrated to be correct, but whose rigorous and general derivation (and, consequently, full understanding) is still lacking.
BIBLIOGRAPHY:
(i) M. Gell-Mann and C. Tsallis, eds., Nonextensive Entropy-Interdisciplinary Applications (Oxford University Press, 2004);
(ii) J.P. Boon and C. Tsallis, eds., Nonextensive Statistical Mechanics-New Trends, New perspectives, Europhysics News 36 (6)(2005)[http://www.europhysicsnews.com/];
(iii) C. Tsallis, M. Gell-Mann and Y. Sato, Proc. Natl. Acad. Sc. (USA) 102, 15377 (2005);
(iv) L.G. Moyano, C. Tsallis and M. Gell-Mann, Europhys. Lett. 73, 813 (2006);
(v) [http://tsallis.cat.cbpf.br/biblio.htm]. |
|
| Marta Tyran-Kaminska (University of Silesia) | Wednesday 5th July 09:50 |
| Statistical limit theorems for non-invertible transformations |
| Given a probability measure preserving transformation and a measurable
observable we give general conditions for validity of statistical
limits theorem, such as CLT and its generalizations, and address the
question when the limit is either the normal distribution, or a
mixture of normal distribution, or alpha-stable distributions. |
|
| Sabir Umarov (National University of Uzbekistan) | Thursday 6th July 18:00 |
| Limit theorems in nonextensive statistical mechanics |
| In the talk we will speak on the q-generalizations of the
classic central limit theorem (CLT) and the Levy-Gnedenko central
limit theorem. The classic central limit theorem plays a fundamental
role in the probability and statistics and in the Boltzmann-Gibbs
statistical mechanics. C.Tsallis introduced in 1988, the
q-entropy, which in the particular case q=1 coincides
with the classic Boltzmann-Gibbs entropy. One of the main requirements
in the classic CLT is the independence of random variables. In the
q-theory random variables are not independent (even not
asymptotically independent). We formulate a q-generalization of
the CLT, which works in the case of globally correlated random
variables, thus consistent with the nonextensive statistical
mechanics. We also generalize a q-version of the classic Levy
stable symmetric distributions describing these in terms of
q-Gaussians.
|
|
| Henk van Beijeren (Universiteit Utrecht) | Tuesday 4th July 10:50 |
| Chaos and the physics of non-equilibrium systems |
| After a brief introduction to chaos theory I will summarize some of the methods for relating it to non-equilibrium statistical mechanics. Then I will show how to use kinetic theory methods to calculate characteristic chaotic properties such as Lyapunov exponents and Kolmogorov-Sinai entropies for dilute interacting particle systems. For the Lorentz gas (a system of light point particles moving among fixed scatterers) these calculations are especially simple, but they can also be done for systems of moving hard spheres. Finally, I will consider the case of the Brownian motion of one large sphere in a very dilute gas of small spheres. Under these conditions the largest Lyapunov exponents are due to the Brownian particle. They can be calculated by solving a Fokker-Planck equation.
|
|
| Sebastian van Strien (University of Warwick) | Wednesday 5th July 11:25 |
| On the Palis conjecture |
| The Palis conjecture states that any one-dimensional system can be perturbed to one which is structurally stable (hyperbolic) and which has a finite number of physical measures. In this talk I will give an update about the current state of play. |
|
| Evgeny Verbitskiy (Philips Research Europe - Eindhoven) | Monday 10th July 18:00 |
| Thermodynamics of hidden Gibbs states |
| Functions of Markov sources, and more generally, of the Gibbs
sources, appear frequently in various fields: Dynamical
Systems, Statistical Mechanics, Information Theory, Statistics.
In this talk I will report on ongoing work establishing
thermodynamic properties of the output processes:
large deviations, variational principles, entropy computation.
|
|
| Franco Vivaldi (Queen Mary, University of London) | Thursday 6th July 12:00 |
| Regular and anomalous transport from space discretization |
| We survey some results on the transport process obtained by discretising the phase space a dynamical system (round-off errors). The system under
consideration is the planar rotation (harmonic oscillator). Space discretization induces a very rich dynamics, which features interesting arithmetical and probabilistic phenomena.
|
|
| Holger Waalkens (University of Bristol) | Wednesday 12th July 17:10 |
| Theory of classical and quantum reaction dynamics in multidimensional systems |
| A general theory for computing the phase space structures that govern
classical reaction dynamics in systems with an arbitrary (finite)
number of degrees of freedom is presented. The theory is based on a
dynamical systems approach to transition state theory which was
invented originally by Wigner and Eyring in the 1930's to compute
chemical reaction rates. The theory presented is algorithmic in nature
and provides, among other things, a solution to the long-standing
problem of how to construct a dividing surface for multidimensional
systems which has all of the properties that are crucial for
reaction-rate computations, i.e., the dividing surface locally divides
the energy surface into two disjoint components that correspond to
"reactants" and "products," it is crossed exactly once by trajectories
in order to react from one component to the other (it is locally a
"surface of no return"), and it is of minimal (directional) flux. The
theory also provides a procedure to compute the global phase space
transition pathways that trajectories must follow in order to
react. The latter are enclosed by the stable and unstable manifolds of
a so-called normally hyperbolic invariant manifold (NHIM). A
description of the geometrical structures and the resulting
constraints on reaction dynamics is given. The theory is based on the
exact Hamiltonian dynamics and allows one to study fundamental
questions in reaction rate theory, such as the violation of ergodicity
assumptions, and non-Markovian behaviour, in a rigorous and
computationally efficient way. Moreover, the classical phase space
structures form a skeleton for quantum mechanical wavefunctions. A
quantum mechanical version of the algorithm that leads to the
construction of the classical phase space structures provides an
efficient procedure to compute quantum reaction rates, the associated
Gamov-Siegert resonances, and the corresponding scattering and
resonance states that become accessible in current high-resolution
experiments.
|
|
| Charles Walkden (University of Manchester) | Tuesday 11th July 12:00 |
| Some uniform ergodic theorems |
(Joint work with Sara Santos)
We prove some topological variants of the Wiener-Wintner
Ergodic Theorem, generalising some results of Peter Walters. |


 .75, not as
.75, not as