Project III 2020-21

The path integral approach to quantum mechanics
and quantum field theory

(Paul Heslop)

Description

The path integral formulation is a beautiful and powerful description of quantum mechanics in which the probability of a particle going from A to B is obtained simply by integrating over all paths from A to B, weighted by the exponential of the action evaluated on each path.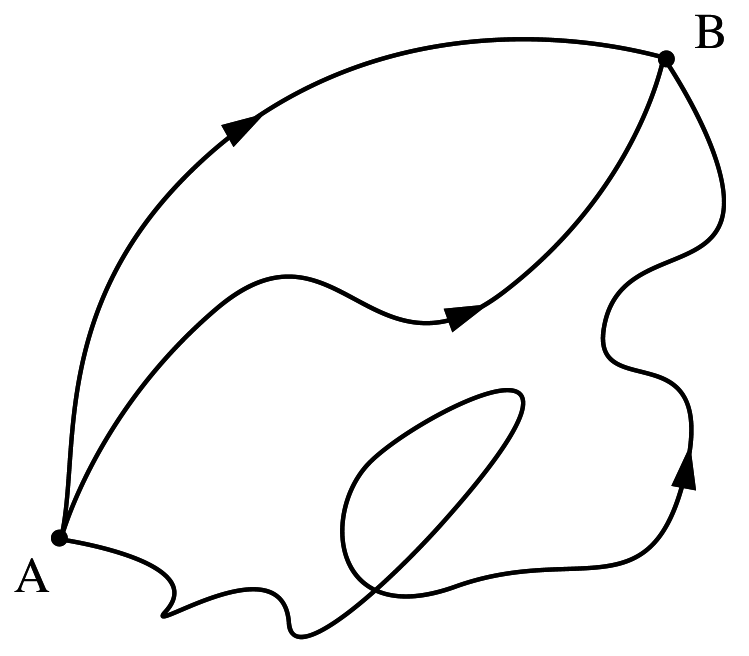

In this project we will begin by investigating the path integral in quantum mechanics, comparing it with the Schroedinger equation. To do this you will need the operator notation you will be learning concurrently in your QMIII course. Later we will take a look at quantum field theory from a path integral point of view.

Pre-requisites

Mathematical Physics II
Special Relativity And Electromagnetism II (not essential but will be useful for when we turn to QFT)

Co-requisites

Quantum Theory III

If you are unsure about the pre- and co-requisites please feel free to get in touch.

Resources

The above wikipedia page is a great start, and then also this one. but you will probably need to learn the operator formalism and bra-ket notation before understanding the details of this.
Feynman Hibbs: Quantum Mechanics and Path Integrals (online pdf version) This is a great place to start!

email: Paul Heslop