Description
An Aztec diamond of size n consists of the squares of the square grid whose centers satisfy {(x,y): |x|+|y| < n+1}. This shape is tileable by dominoes, meaning that dominoes are arranged on the Aztec diamond so that each square is covered exactly once by a domino. Uniformly random domino tilings of very large Aztec diamonds macroscopically lead to a disordered region within an inscribed circle and a regular brick-like region outside the circle. This is known as the Arctic circle theorem: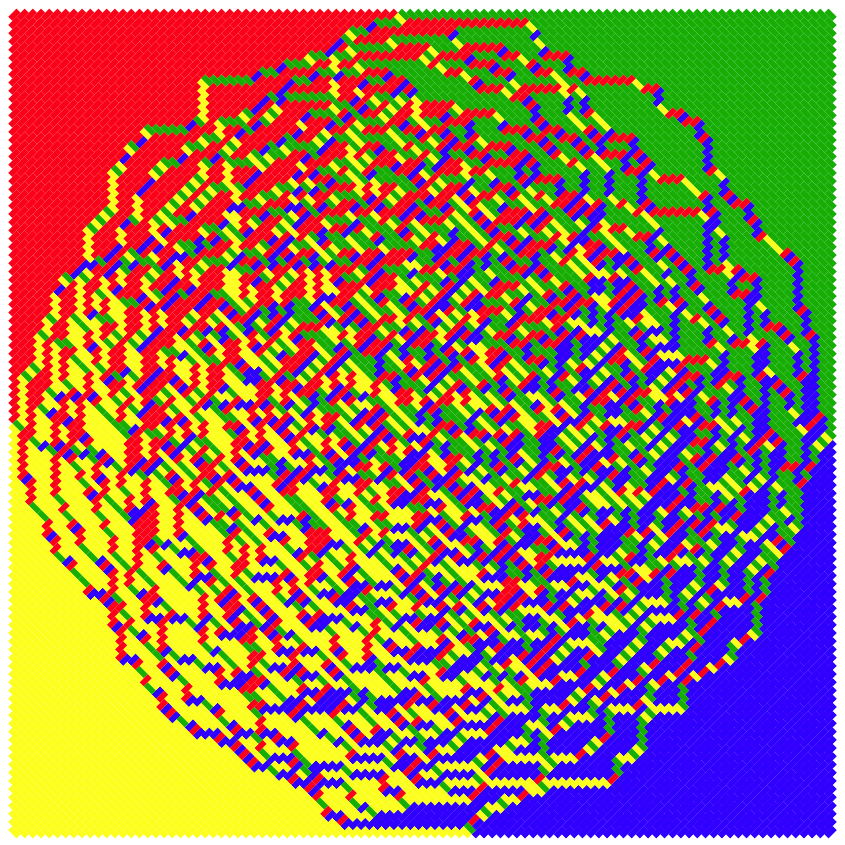
A domino tiling of the Aztec diamond of size 100 (rotated 45 degrees)
The aim of this project is to explore this and perhaps other related models. There are many potential directions of study within probability and combinatorics depending on one's taste. Some avenues of possible investigation include but are certainly not limited to:
- counting the number of domino tilings of an Aztec diamond of size n and comparing with related models
- understanding one of the many proofs of the arctic circle theorem
- studying determinantal point processes and their connection to random tilings
- exploring other tiling models such as lozenge tilings
- fluctuations at the border of the Arctic circle theorem
- simulating domino tilings of Aztec diamonds and domino tilings of other regions
Prerequisites
2H Probability is essential; 3H Stochastic Processes is desirable.Resources
- N. Elkies, G. Kuperberg, M. Larsen, J. Propp, Alternating-sign matrices and domino tilings; Journal of Algebraic Combinatorics, Vol 1, no.2, 1992.
The original paper introducing the Aztec diamond giving different approaches to count the number of tilings. - A. Björner and R.P.Stanley, A combinatorial miscellany, L'Enseignement mathématique 2010, available online at http://www-math.mit.edu/~rstan/papers/comb.pdf
A combinatorics book giving a good overview of domino tilings; see Chapters 8 and 9. - W. Jockusch, J. Propp and P. Shor, Random domino tilings and the arctic circle theorem, http://arxiv.org/abs/math/9801068
A preprint giving the first proof of the arctic circle theorem. Since then, there have been many different proofs. This proof connects nicely to other probabilistic models. - K. Johansson, Random matrices and determinantal point processes, Mathematical Statistical Physics, Session LXXXIII: Lecture Notes of the Les Houches Summer School 2005, available online at http://arxiv.org/abs/math-ph/0510038
Introduces point processes and the methods used to study fluctuations at the border of the Arctic circle. - J. Propp, Generalized domino shuffling, available online at
http://arxiv.org/abs/math/0111034
This article introduces a method to simulate rather general domino tilings of Aztec diamonds.
Get in touch, if have any questions and/or if you would be interested in doing simulations!