4 Linear Lie groups and their Lie algebras 4.6 Topological properties 5 Representations of Lie groups and Lie algebras - generalities

4.7 The example of SU(2) and SO(3)

We illustrate the previous section with the example of $\mathrm{SO}(3)$ . According to Table 4.6, the fundamental group of $\mathrm{SO}(3)$ is $C_{2}$ . We can visualize this as follows: An element of $\mathrm{SO}(3)$ is rotation by some angle $\theta\in[0,\pi]$ about some (oriented) axis. We can represent this as a vector in $\mathbb{R}^{3}$ of length $\theta$ in the direction of the axis. Elements of $\mathrm{SO}(3)$ then correspond to points in the closed ball in $\mathbb{R}^{3}$ of radius $2\pi$ . However, rotation by $\pi$ about the axis $v$ is the same as rotation by $\pi$ about the axis $-\pi$ , and so we must identify diametrically opposite points on the boundary of this ball.

Figure 4: Picture of

\mathrm{SO}(3)

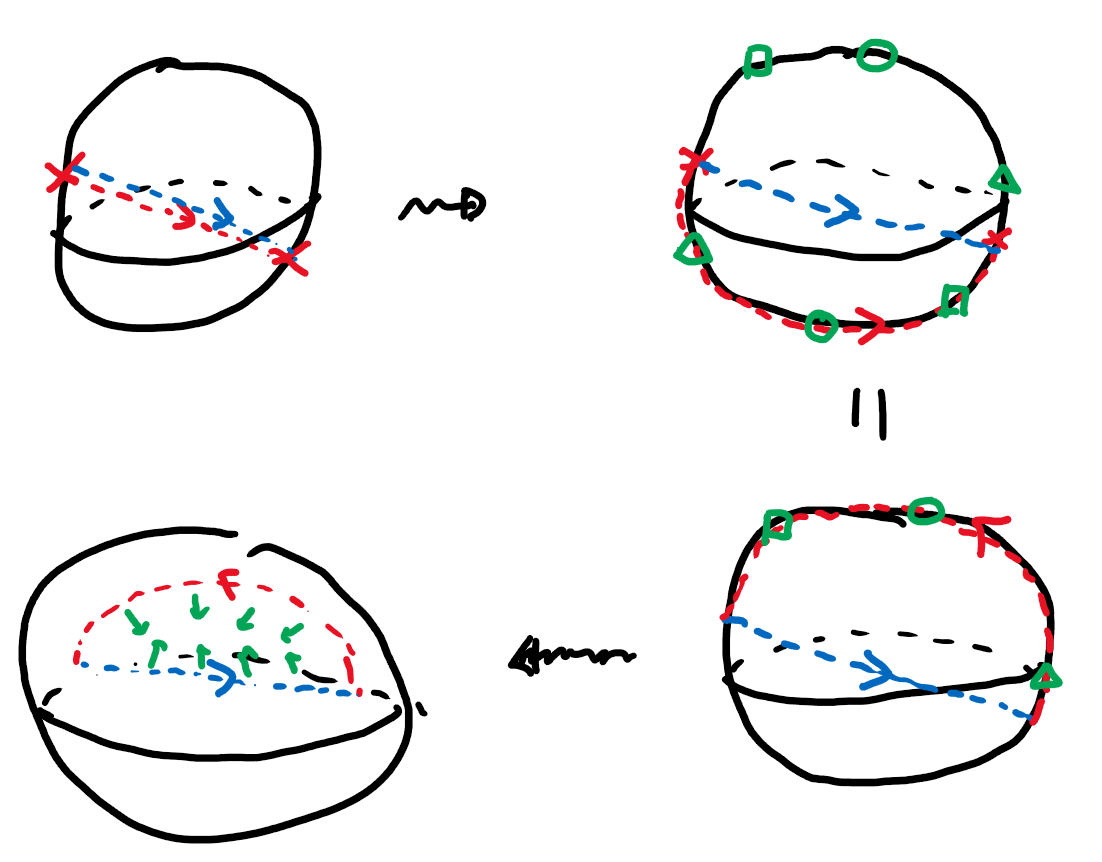
Now, the straight line in this three-dimensional sphere from a point on the boundary to its diametrically opposite point is a loop in $\mathrm{SO}(3)$ since the endpoints represent the same rotation. You can convince yourself that this loop cannot be shrunk to a point (proving it rigorously requires some topology). However, if you go around the loop twice, then that can (!) be shrunk to a point. The idea is to move one copy of the loop out to the boundary, then use the ‘opposite point’ identification to move it to the other side, when you get a normal loop inside the ball which may be shrunk. See Figure 5.

A nice physical illustration of this is provided by the “Dirac belt trick”; here is a video of this demonstrated with long hair!

According to the general picture of the previous section, there should be a Lie group homomorphism $\tilde{G}\to\mathrm{SO}(3)$ whose kernel has order 2 and such that $\tilde{G}$ is simply connected, and it turns out that we can take $\tilde{G}=\mathrm{SU}(2)$ . So we study this group for a bit.

Firstly, one can show (see problem 62) that every element of $\mathrm{SU}(2)$ has the form

\begin{pmatrix}a&-\overline{b}\\ b&\overline{a}\end{pmatrix}

for $a,b\in\mathbb{C}$ with $|a|^{2}+|b|^{2}=1$ . It follows that $\mathrm{SU}(2)$ is diffeomorphic to the unit sphere $S^{3}$ in $\mathbb{R}^{4}$ , which is simply connected.

We would like to write down a homomorphism $\mathrm{SU}(2)\to\mathrm{SO}(3)$ . For this, we want to find a three-dimensional real vector space $V$ , equipped with an inner product (i.e. a positive definite, symmetric, bilinear form) that is preserved by the action of $\mathrm{SU}(2)$ . If we write down an orthonormal basis for $V$ , then the matrix of the action of each element of $\mathrm{SU}(2)$ on $V$ , with respect to this basis, will be an element of $\mathrm{SO}(3)$ giving the required homomorphism.

Where can we find $V$ ? From $\mathrm{SU}(2)$ itself! We take $V=\mathfrak{su}_{2}$ , a three-dimensional vector space (by problem 56), and let $\mathrm{SU}(2)$ act on $V$ via conjugation. We just need an inner product, and we may define one as follows: for $X,Y\in\mathfrak{su}_{2}$ , let

\left\langle X,Y\right\rangle=-\operatorname{tr}(XY).

Exercise 4.57.

Show that this is a symmetric, positive definite bilinear form on $\mathfrak{su}_{2}$ .

Show that it is preserved by the action of $\mathrm{SU}(2)$ , i.e. that

\left\langle gXg^{-1},gYg^{-1}\right\rangle=\left\langle X,Y\right\rangle

for all $g\in\mathrm{SU}(2)$ .

We therefore obtain a homomorphism $\pi:\mathrm{SU}(2)\to\mathrm{SO}(3)$ once we fix an orthonormal basis; may be taken to be the matrices

\frac{1}{\sqrt{2}}\begin{pmatrix}i&0\\ 0&-i\end{pmatrix},\frac{1}{\sqrt{2}}\begin{pmatrix}0&1\\ -1&0\end{pmatrix},\frac{1}{\sqrt{2}}\begin{pmatrix}0&i\\ i&0\end{pmatrix}.

Exercise 4.58.

Write down explicitly the image of $\begin{pmatrix}a&-\overline{b}\\ b&\overline{a}\end{pmatrix}$ under this homomorphism.

Finally, one can check that it has the right kernel:

Exercise 4.59.

Show that, if $g\in\mathrm{SU}(2)$ satisfies $gXg^{-1}=X$ for all $X\in\mathfrak{su}_{2}$ , then $g=\pm I$ . Deduce that

\ker(\pi)=\{\pm I\}\cong C_{2}.