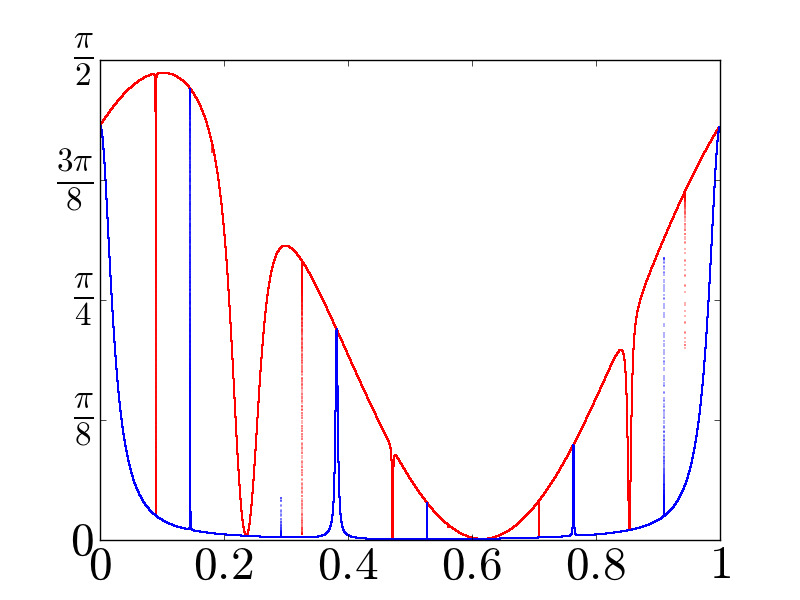
![ϕ: (θ,x) ↦→ (θ+ ω,arctan[100x- β(1+ cos2πθ)])](low-dim-dynamics-30x.png)
defined on the closed cylinder X = T1 × [-π ∕ 2,π ∕ 2] (where T1 is the circle—plotted as the unit interval [0,1] with identified endpoints). Here, ω is the golden mean and β some real number whose exact value no one knows.
Description.
In the simplest case, a dynamical system is nothing but a continuous self-map
ϕ : X → X on some (compact) metric space X. If you prefer it less abstract, in this
project, X will often be the circle, the 2-torus or more generally, some surface.
The overall goal of the theory of dynamical systems is to develop purely
mathematical tools to understand qualitatively how points x ∈ X move as we
iteratively apply the map ϕ to x. In this sense, one may understand ϕ as the
law of time evolution, where time (0,1,2,…, i.e. the natural numbers) is
thought of as being discrete. Depending on ϕ, the qualitative behaviour may be
very regular (as for rotations on the circle) or chaotic (as in the case of the
so-called cat map on the 2-torus). It is the goal of this project to get to know
techniques to analyse some of the infinitely many phenomena that occur in a
low dimensional setting. Often, these phenomena are way more fascinating
than one may think when taking a look at the map ϕ itself, see the below
figure for an example.
defined on the closed cylinder X = T1 × [-π ∕ 2,π ∕ 2] (where T1 is the circle—plotted
as the unit interval [0,1] with identified endpoints). Here, ω is the golden mean and β
some real number whose exact value no one knows.

![ϕ: (θ,x) ↦→ (θ+ ω,arctan[100x- β(1+ cos2πθ)])](low-dim-dynamics-30x.png)
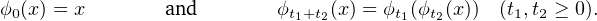 | (1) |
In simple terms, the first equality just means that if no time elapses, nothing should change, while the second equality means that the law which governs the time evolution is itself independent of time. In fact, one can generalise (1) considerably but this is not too much the point in this project (although, if you like algebra, this is definitely a possible way to go).
There are plenty of different directions you can take in this project, depending on your interests. Some natural topics include rotation theory (on the circle but also the 2-torus—here, there is a lot of space to work on classical topology in the plane), Poincaré Bendixson Theory (if you like differential equations), twist maps (and their relation to billiards), combinations of all this or something completely different.
Pre-/Co-requisites. It is ideal if you take Topology 3, in particular, notions such as compactness and continuity will naturally play a prominent role. If you don’t take Topology 3, you may still go for this project as you don’t necessarily need too much background (and may know the essentials from your analysis courses) as long as you’re willing to study any possibly missing concept. Depending on which way your project develops, you may need some basic knowledge of ordinary differential equations (as in Dynamical Systems III) but this is no necessity at all. Measure theory can be very helpful but again, it is not necessary.
References. For a start, you may consult some of the plenty of excellent textbooks on dynamical systems in general. Among those, [1] and [2] provide chapter(s) specifically dedicated to low dimensional dynamics. To approach the topic from the perspective of differential equations, [3] would be a classical choice. For all these books, the library provides online access.
[1] Anatole Katok and Boris Hasselblatt. Introduction to the modern theory of dynamical systems, volume 54 of Encyclopedia of Mathematics and its Applications. Cambridge University Press, Cambridge, 1995.
[2] Michael Brin and Garrett Stuck. Introduction to dynamical systems. Cambridge University Press, Cambridge, 2002.
[3] Philip Hartman. Ordinary differential equations, volume 38 of Classics in Applied Mathematics. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA, 2002.