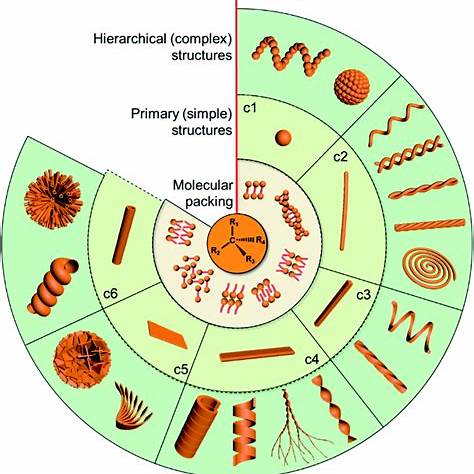
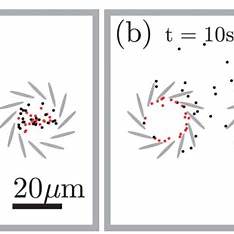
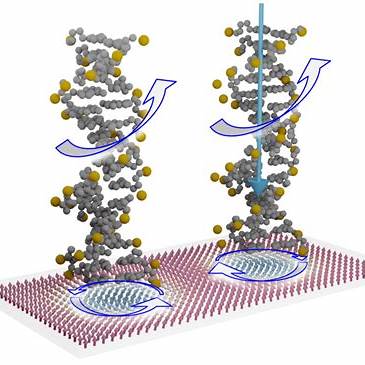
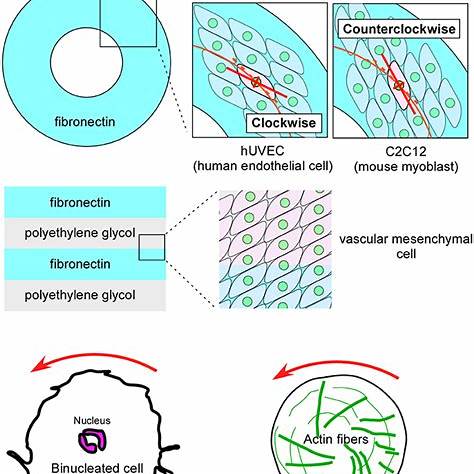
This project explores reaction‑diffusion modelling in chiral systemssuch as DNA nano‑triangles, cholesteric liquid crystals, and certain bacterial coloniesthat exhibit handed (left/right) spatial patterns due to molecular asymmetry.




Models typically combine reaction‑diffusion partial differential equations with chirality‑inducing mechanisms: anisotropic diffusion, twisted interaction terms, or coupling with orientation fields (e.g., nematic alignment in soft matter). Some discrete models use biased hopping or chiral reaction asymmetries. These are often studied through linear stability analysis and numerical simulation.
Students interested in computational modelling, scientific programming (e.g., Python, MATLAB), and pattern formation are encouraged to apply. Prior experience in mathematical biology is helpful but not essentialcuriosity and motivation are most important.