Description

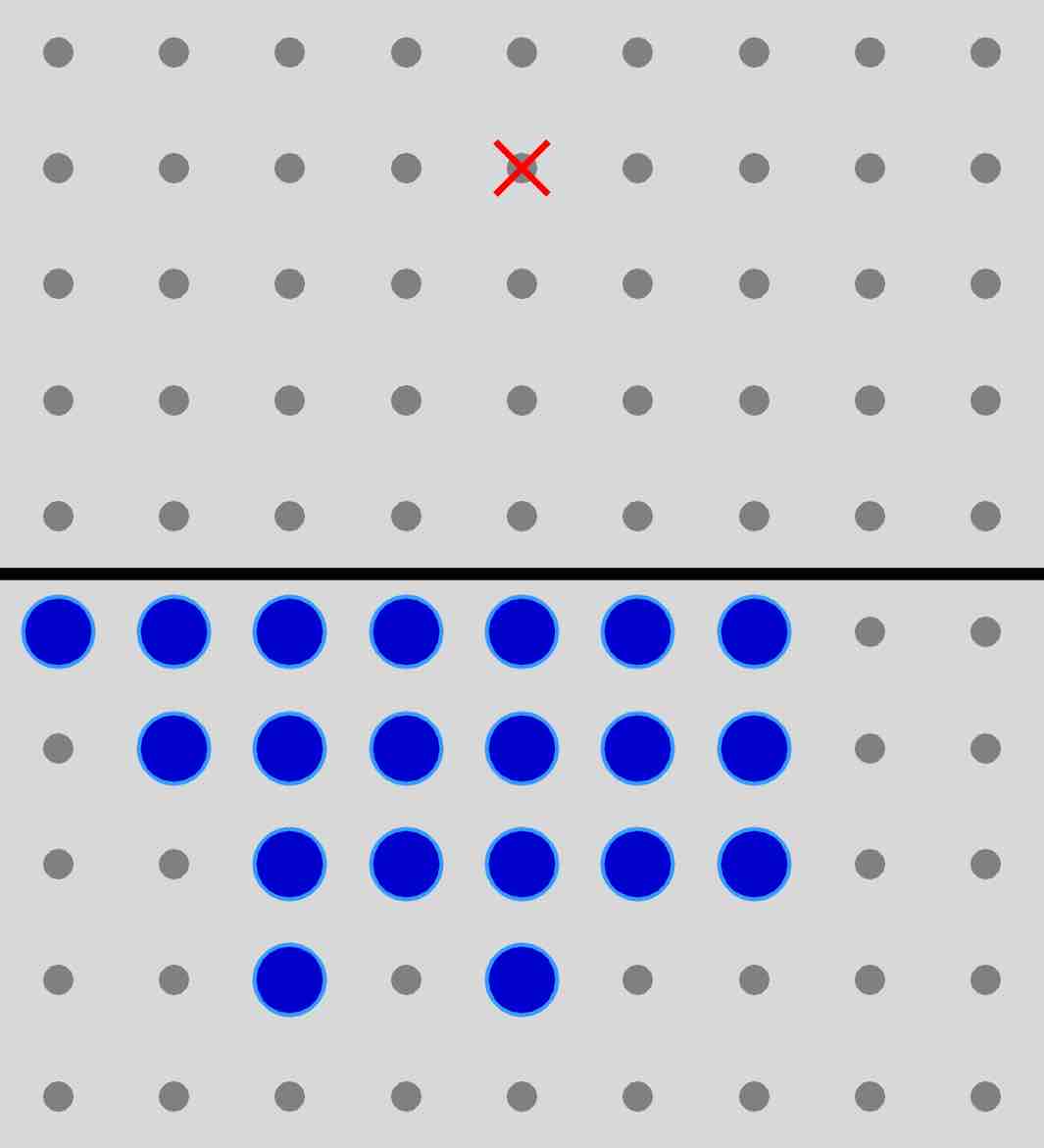
This project concerns a simple puzzle, known as "solitaire army" or Conway's soldiers: what is the minimum number of "pegs" needed to reach a target position on a square lattice, if they all have to start below a line? Each move must consist of a single peg jumping over another peg, either left, right, up or down. The peg jumped over is removed from the board.

The picture on the left shows a (minimal) starting configuration that can reach the target square shown, located four rows above the line. (Can you find the correct sequence of jumps?)

Solitaire army is interesting from a mathematical point of view because the mathematician John Horton Conway came up with an elegant way of analysing the problem, allowing him to prove that it is impossible to reach row five with any finite number of pegs!

In this project, we will begin by studying Conway's proof, and individual students will then be able to take it in different directions. For example, Tatham and Taylor recently showed that row five can be reached if you allow an infinite number of starting pegs. Or there are many ways to generalize the problem, such as allowing diagonal moves, increasing the number of dimensions, or changing the shape of the starting region.

These solitaire problems turn out to be intrinsically difficult: indeed, the problem of deciding whether a particular initial configuration of pegs can reach a particular target position has recently been proven to be NP-complete.

Prerequisites

None but some experience of coding in (e.g.) Python would be useful.

Resources

There is a description of the problem on Wikipedia, with some good further links. You can read about it in the article Moving into the Desert with Fibonacci (Aigner, Mathematics Magazine 70, p11, 1997), or in the books Nonplussed! by Julian Havil and Winning ways for your mathematical plays by Berlekamp, Conway and Guy. Another useful web page is maintained by George Bell.