Winding gauge for the Lundquist field
Consider a magnetic field \({\bf B}\) on a cylinder \(\mathcal{C}\) with \(B_r=0\) on the side boundary \(r=R.\) Such a magnetic field admits a vector potential of the form \[ {\bf A}^W({\bf x}) = \frac{1}{2\pi}\int_{S_z}\frac{{\bf B(y)}\times{\bf r}}{|{\bf r}|^2}\,\mathrm{d}^2y, \qquad {\bf r}={\bf x}-{\bf y} \qquad(*) \] which Prior & Yeates (2014) called the winding gauge. I recently wanted to compute this vector potential for the Lundquist linear-force free field \({\bf B} = J_0(\alpha r){\bf e}_z + J_1(\alpha r){\bf e}_\phi,\) where \(J_0\) and \(J_1\) are Bessel functions.
First, let me tell you the answer. It seems to be \[ {\bf A}^W = \alpha^{-1}\Big[J_0(\alpha r) - J_0(\alpha R)\Big]{\bf e}_z + \alpha^{-1}J_1(\alpha r){\bf e}_\phi. \] Notice that this is remarkably similar to the “obvious” vector potential \({\bf A} = \alpha^{-1}{\bf B},\) which one has for any linear force-free field. The extra constant has the effect of setting \(A^W_z=0\) on the boundary.
It is easy to calculate the field line helicity in both these gauges. Specifically, if \(L\) is the length of the cylinder then for \({\bf A}\) and \({\bf A}^W\) we have \[ \mathcal{A}(r) = \frac{L}{\alpha}\left(J_0(\alpha r) + \frac{J_1^2(\alpha r)}{J_0(\alpha r)}\right), \qquad \mathcal{A}^W(r)=\mathcal{A}(r) - \frac{L}{\alpha}J_0(\alpha R). \] In the remainder of this post, I want to first discuss the (slightly subtle) relation of these vector potentials to the “minimal gauge” of Yeates & Page (2018). Then I will explain how I calculated \({\bf A}^W\) numerically and verified that it matches the above expression. My code works for any magnetic field on a cylinder.
Relation to the minimal gauge
Since our domain \(\mathcal{C}\) is not magnetically closed (at the ends), the field line helicity is not gauge invariant. However, Yeates & Page (2018) noted that the field line helicity in a simply-connected domain like this is uniquely specified by fixing the tangential vector potential \({\bf n}\times{\bf A}\) on the boundary \(\partial\mathcal{C}.\) And we showed that the condition \(\nabla_h\cdot{\bf A}=0\) (vanishing tangential divergence) on \(\partial\mathcal{C}\) is sufficient to make the field line helicity unique. This was dubbed the “minimal” gauge condition because it corresponds to minimising the 2-norm of \({\bf n}\times{\bf A}\) on \(\partial\mathcal{C}.\) The same condition was introduced previously by Hornig (2006) in his “universal helicity”.
I bring this up here because it turns out that, for the Lundquist field, \({\bf A}^W\) satisfies the minimal gauge condition, while \({\bf A}=\alpha^{-1}{\bf B}\) does not. At first glance, it seems that both satisfy \(\nabla_h\cdot{\bf A}=0,\) because both of these vector potentials satisfy this condition on each of the end faces of the cylinder and also on the side boundary. However, you have to be careful at the edges where the side and end faces meet.
At these edges, the surface \(\partial\mathcal{A}\) is not smooth, so we have to consider the analogous integral condition, which requires that \(\int_D\nabla_h\cdot{\bf A}\,\mathrm{d}S=0\) over every subregion \(D\subset\partial\mathcal{C}.\) (A similar consideration applies when computing the minimal gauge on a Cartesian box, as in the Yeates & Page paper.) If we take \(D\) to lie wholly on one of the ends of the cylinder, or wholly on the side, then this condition will be satisfied by both \({\bf A}\) and \({\bf A}^W.\) But consider what happens if we take it to straddle the edge, as in the sketch below:
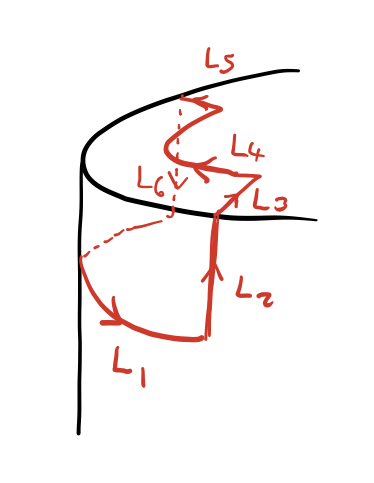
Applying the divergence theorem, we see that \(\int_D\nabla_h\cdot{\bf A}\,\mathrm{d}S = \oint_{\partial D}{\bf A}\cdot{\bf n}\,\mathrm{d}l.\) The contributions from \(L_2\) and \(L_6\) cancel, because \(A_\phi\) is independent of \(\phi\) (for both vector potentials). Similarly \(L_3\) and \(L_5.\) There is no contribution from \(L_4\) since \(A_r=0\) for both vector potentials. But there is an unbalanced contribution from \(L_1\), so that \(\int_D\nabla_h\cdot{\bf A}\,\mathrm{d}S = -\int_{L_1}A_z R\,\mathrm{d}\phi = -R|L_1|A_z(R).\) This vanishes for \({\bf A}^W,\) since \(A^W_z(R)=0,\) but it does not vanish for \({\bf A}=\alpha^{-1}{\bf B}.\) Thus \({\bf A}^W\) satisfies the minimal gauge condition while the other vector potential does not. Indeed we already saw that it gives a different field line helicity.
From the topological point of view, the requirement that \(A^W_z(R)=0\) is a natural one: it effectively says that the corresponding field line helicity measures only winding of magnetic flux within the cylindrical domain. Non-zero \(A_z(R)\) implies that there is magnetic flux outside the domain, so that the corresponding field line helicity will include a contribution from linkage with that flux. An analogous situation arises when calculating helicity of toroidal magnetic fields.
Note. For a general magnetic field on \(\mathcal{C},\) I don’t see why the winding gauge should satisfy the minimal gauge condition. But it seems likely to be true for any magnetic field that depends only on \(r\).
Calculation of \(\mathcal{A}^W\)
Suppose we want to compute \({\bf A}^W(x_1, x_2, z).\) Rather than approximating the integrals (*) directly, is is better to change to polar coordinates centered at the point \({\bf x}=(x_1,x_2,z).\) For the Lundquist field I can ignore \(z,\) and since the field is axisymmetric it follows that \({\bf A}^W\) will depend only on \(r,\) so that without loss of generality I can set \(x_2=0\) and focus on the \(x_1\) axis to determine the radial profile.
Setting \(x_2=0\) I have \[ {\bf B}\times{\bf r} = y_2B_z({\bf y}){\bf e}_1 + (x_1-y_1)B_z({\bf y}){\bf e}_2 - \Big[y_2B_1({\bf y}) + (x_1-y_1)B_2({\bf y})\Big]{\bf e}_z. \] Then \[\begin{align*} A^W_1({\bf x}) &= \frac{1}{2\pi}\int\frac{y_2B_z({\bf y})}{(x_1-y_1)^2 + y_2^2}\,\mathrm{d}^2y,\\ A^W_2({\bf x}) &= \frac{1}{2\pi}\int\frac{(x_1-y_1)B_z({\bf y})}{(x_1-y_1)^2 + y_2^2}\,\mathrm{d}^2y,\\ A^W_z({\bf x}) &= -\frac{1}{2\pi}\int\frac{y_2B_1({\bf y}) + (x_1-y_1)B_2({\bf y})}{(x_1-y_1)^2 + y_2^2}\,\mathrm{d}^2y. \end{align*}\] Now we change to polar coordinates centered at \({\bf x},\) namely \[ y_1 = r\cos\phi + x_1, \qquad y_2 = r\sin\phi. \] The purpose of this coordinate change is to make the integrands non-singular, since we find \[\begin{align*} A^W_1({\bf x}) &= \frac{1}{2\pi}\int B_z({\bf y})\sin\phi\,\mathrm{d}r\mathrm{d}\phi,\\ A^W_2({\bf x}) &= -\frac{1}{2\pi}\int B_z({\bf y})\cos\phi\,\mathrm{d}r\mathrm{d}\phi, \\ A^W_z({\bf x}) &= \frac{1}{2\pi}\int \Big[B_2({\bf y})\cos\phi - B_1({\bf y})\sin\phi\Big]\,\mathrm{d}r\mathrm{d}\phi. \end{align*}\] These integrals can then be evaluated numerically. I do the \(r\) integral first, noting that the upper limit depends on \(\phi.\) It takes the form \[ r_{\rm max}(\phi) = -x_1\cos\phi + \sqrt{x_1^2\cos^2\phi + R^2 - x_1^2}, \] which you can derive by simultaneously solving \(y_1^2 + y_2^2 = R^2\) and \((x_1-y_1)^2 + y_2^2 = r^2.\)
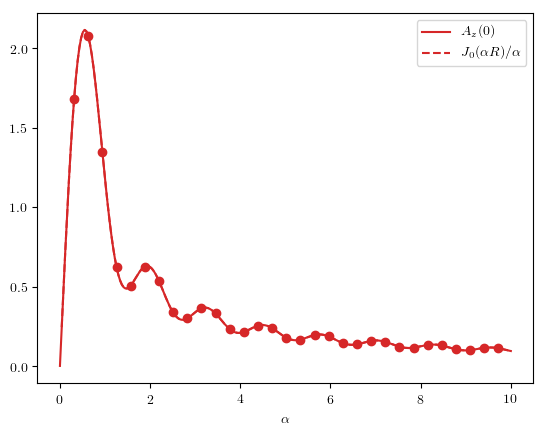
With the composite trapezium rule, here are the results for the Lundquist solution with \(\alpha=0.4:\)
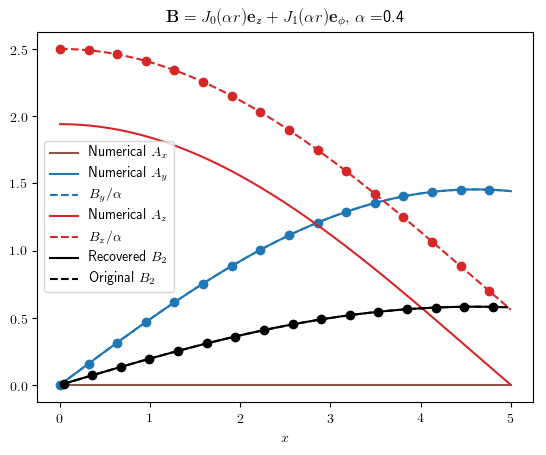
Here the “numerical” results show the values computed with the above integrals. The red and blue dashed lines with dots show the vector potential \({\bf A}=\alpha^{-1}{\bf B}.\) Since we are on the \(x_1\) axis, the component \(A_x\) corresponds to \(A_r\) in cylindrical coordinates, and \(A_y\) to \(A_\phi.\)
You can see that the \(A_y\) components agree between the two vector potentials, but the \(A_z\) components have a constant offset, corresponding to the different boundary condition. In the plot below, I compute the offsets numerically as a function of \(\alpha,\) and compare them to the exact formula given at the start of this post. Here \(A_z(0)\) means the numerically-computed \(A^W_z\) evaluated at \(r=0.\)
