$$ \def\ab{\boldsymbol{a}} \def\bb{\boldsymbol{b}} \def\cb{\boldsymbol{c}} \def\db{\boldsymbol{d}} \def\eb{\boldsymbol{e}} \def\fb{\boldsymbol{f}} \def\gb{\boldsymbol{g}} \def\hb{\boldsymbol{h}} \def\kb{\boldsymbol{k}} \def\nb{\boldsymbol{n}} \def\pb{\boldsymbol{p}} \def\qb{\boldsymbol{q}} \def\rb{\boldsymbol{r}} \def\tb{\boldsymbol{t}} \def\ub{\boldsymbol{u}} \def\vb{\boldsymbol{v}} \def\xb{\boldsymbol{x}} \def\yb{\boldsymbol{y}} \def\zb{\boldsymbol{z}} \def\Ab{\boldsymbol{A}} \def\Bb{\boldsymbol{B}} \def\Eb{\boldsymbol{E}} \def\Fb{\boldsymbol{F}} \def\Jb{\boldsymbol{J}} \def\Ub{\boldsymbol{U}} \def\xib{\boldsymbol{\xi}} \def\evx{\boldsymbol{e}_x} \def\evy{\boldsymbol{e}_y} \def\evz{\boldsymbol{e}_z} \def\evr{\boldsymbol{e}_r} \def\evt{\boldsymbol{e}_\theta} \def\evp{\boldsymbol{e}_r} \def\evf{\boldsymbol{e}_\phi} \def\evb{\boldsymbol{e}_\parallel} \def\omb{\boldsymbol{\omega}} \def\dA{\;\mathrm{d}\Ab} \def\dS{\;\mathrm{d}\boldsymbol{S}} \def\dV{\;\mathrm{d}V} \def\dl{\mathrm{d}\boldsymbol{l}} \def\bfzero{\boldsymbol{0}} \def\Rey{\mathrm{Re}} \def\Real{\mathbb{R}} \def\grad{\boldsymbol\nabla} \newcommand{\dds}[1]{\frac{\mathrm{d}{#1}}{\mathrm{d}s}} \newcommand{\ddy}[2]{\frac{\partial{#1}}{\partial{#2}}} \newcommand{\ddt}[1]{\frac{\mathrm{d}{#1}}{\mathrm{d}t}} \newcommand{\DDt}[1]{\frac{\mathrm{D}{#1}}{\mathrm{D}t}} $$
Untangling the s-web
Roger Scott from the the University of Dundee gave us an insightful applied mathematics seminar on Friday 19th October, summarizing his work about the open-closed coronal boundary, on which I am a co-author. You can read the full paper on arXiv here (and now in ApJ).
Roger posed the following question: if we look at a latitude-longitude map of the squashing factor \(Q\) at the top of the corona (say, \(2.5 R_\odot\)), what can we infer about the topology of the coronal magnetic field beneath? Here is a picture taken from our paper, showing \(Q\) on four radial slices through a potential-field source surface (PFSS) model. Of course, \(Q\) is always positive; the sign here just indicates whether the magnetic field is open (negative) or closed (positive).
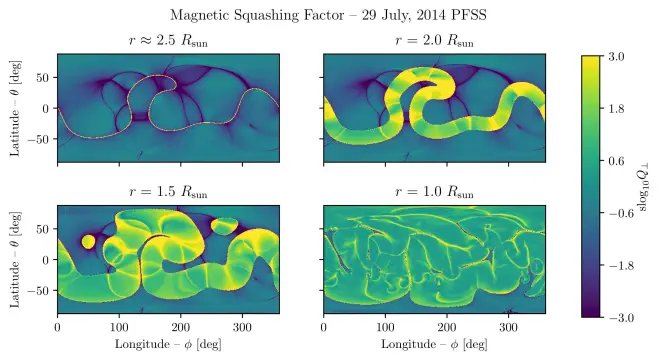
The top left panel is close to the outer boundary of the model, and you can clearly see the yellow line of the heliospheric current sheet (HCS), where the open magnetic field changes sign. You can also see dark lines within the open regions – these are the arcs of the “S-web”, as proposed by Antiochos et al. (2011), who argue that the latitudinal spread of these structures explains the distribution of slow solar wind material. This material has physical characteristics of closed field regions, probably released through interchange reconnection with the open field. The high-\(Q\) arcs are supposed to indicate locations on the outer boundary that map down to sites of interchange reconnection in the corona beneath.
If I had to summarize Roger’s findings, I would say that there are two types of high-\(Q\) arcs:
Simple arcs, that connect to the HCS at both ends, map down to narrow open-field corridors at the photosphere (as per Antiochos et al. (2011)), as in this cartoon:
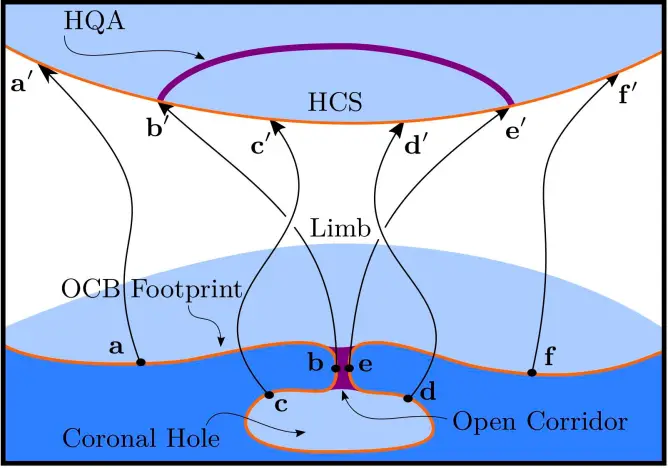
The open-closed boundary on the photosphere has to map continuously to the HCS on the outer boundary, with the consequence that the narrow open-field channel has to stretch out to a long arc on the outer boundary.
Branching structures with vertices away from the HCS indicate the presence of a coronal null dome in the open field region beneath. The vertex lies where the null’s spine line intersects the outer boundary. Here are a couple of examples that Roger showed:
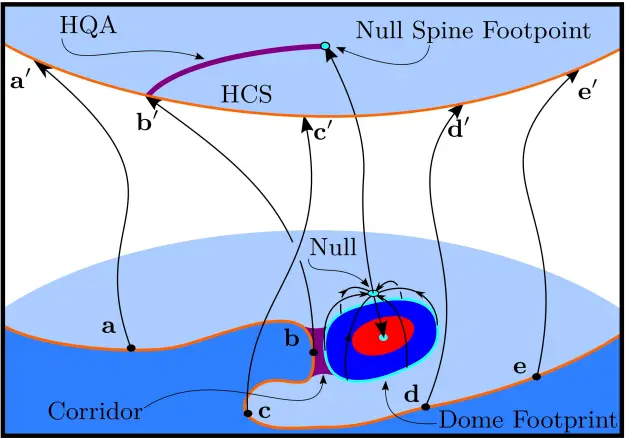
Since the branching structures connect to low-coronal null domes, we might expect reconnection at these locations to release more “slow solar wind” plasma than the simple arcs.
The paper itself gives a lot more detail, of course. One thing that Roger found from analysing PFSS extrapolations is that simple arcs are typically on the “concave” side of the HCS, while branching structures are typically on the “convex” side. You can see this in the example at the top.
Lastly, some thoughts on the practical implications. Computing \(Q\) is far easier than finding the true magnetic skeleton of null points and separatrix surfaces (see this paper by Sarah Edwards for a case where we computed both). This is particularly true when you take advantage (as Roger did) of the approach used in qslSquasher by Svetlin Tassev, which avoids computing numerical derivatives of the field-line mapping. Details are in Svetlin’s original paper as well as Roger’s paper that puts the method on a firm theoretical footing. If you are involved in calculating \(Q\), I strongly suggest to give these a look.