Boundary conditions for potential field extrapolation

Illustrating the difference between a source surface potential field and a typical reference potential field.

I’ve recently updated my spherical PFSS solver to add a new alternative outer boundary condition on the source surface \(r=R_{\rm ss}.\) In addition to the usual “radial field” condition \(B_\theta=B_\phi=0,\) it is now possible to match \(B_r(\theta,\phi)\) to an arbitrary two-dimensional distribution.

This is useful, for example, in studies of magnetic helicity.

The images below show two potential-field extrapolations from the same \(B_r\) on the lower boundary, one using the original radial-field condition and the other with the new outer boundary condition. In this case, I matched the outer \(B_r\) to a non-potential field from a magneto-frictional model. Notice how this new boundary condition allows “u-loops” in the potential field.

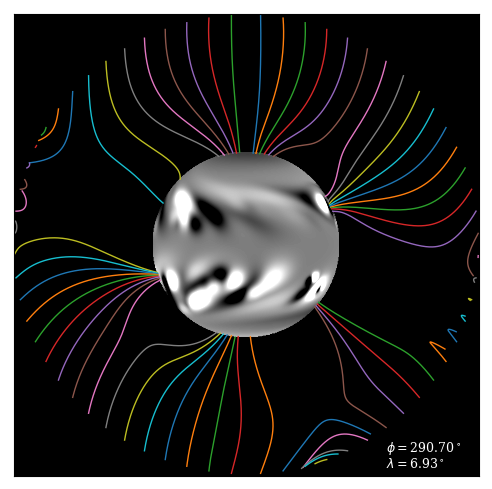
My code is based on the method described in Appendix B of van Ballegooijen et al (2000), and the modification to the new boundary condition was quite straightforward. Instead of using equation (B9) to relate \(C^{(-)}_{lm}\) and \(C^{(+)}_{lm},\) we use orthogonality of the eigenmodes twice, at the inner and outer boundaries. This gives two simultaneous equations for \(C^{(-)}_{lm}, C^{(+)}_{lm}\) which are just solved algebraically. See the manual of my code for more details.

The advantage of the van Ballegooijen method over (say) spherical harmonics is that \(\nabla\times{\bf B}={\bf 0}\) is satisfied to high accuracy when using a particular finite-difference stencil. This is important when using the solution to initialise magneto-frictional simulations, for example.

Finally, I note that David Stansby at Imperial has recently packaged my solver with a bit more of a user interface – see here.