Ideal evolution of the `force-free parameter’

Is the field-line averaged force-free parameter invariant under an ideal, line-tied evolution?

It is well-known that a line-tied magnetic field under ideal MHD will relax to a nonlinear force-free equilibrium where the force-free parameter \(\lambda:={\bf j}\cdot{\bf B}/B^2\) is constant along magnetic field lines, but may differ from one field line to another.

Before \({\bf B}\) has reached a force-free state, the parameter \(\lambda\) will also vary along magnetic field lines, but we can consider its field-line averaged value \[ \lambda^* := \frac{1}{|L|}\int_L\lambda\,\mathrm{d}\ell \] for any field line \(L\) of length \(|L|\). The question is simple: is \(\lambda^*\) invariant under an ideal, line-tied evolution? (Line-tied means that the endpoints of field lines on the boundaries are fixed.) In other words, do the field lines just preserve their average value of \(\lambda\) during the relaxation?

I haven’t managed to find an answer to this question in the literature, but I’m pretty sure that the answer in general is “no“. To show this, I constructed a semi-analytical counter-example, shown in the picture below. I call it “semi-analytical” because \({\bf B}(x,y,z,t)\) and \({\bf j}(x,y,z,t),\) and hence \(\lambda,\) are given by symbolic formulae, but I used numerical integration to average along field lines and compute \(\lambda^*.\) The colours show the value of \(\lambda^*\) on each magnetic field line, in two magnetic fields that are related by an ideal evolution that vanished on the (top and bottom) boundaries. Clearly these values of \(\lambda^*\) change for a given field line, in general.

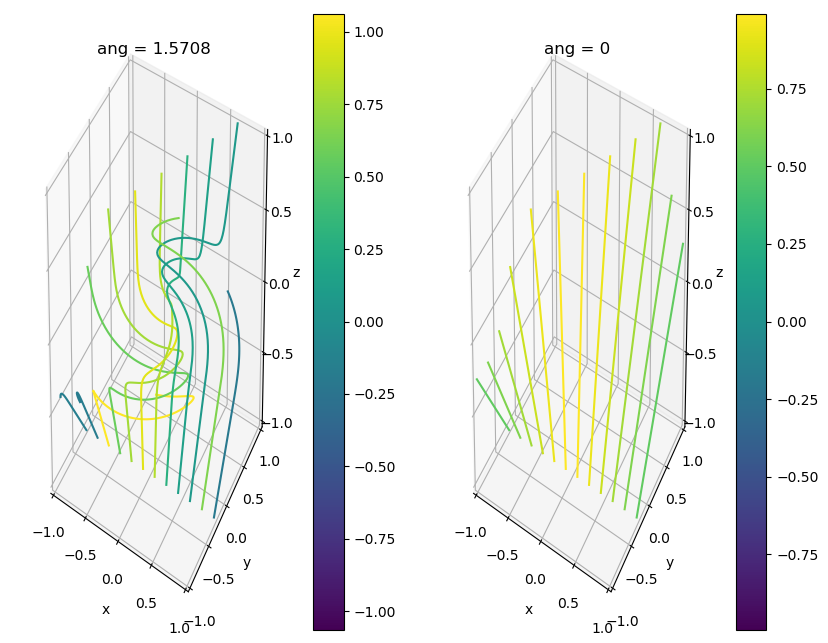
The initial magnetic field \({\bf B}_0 = x\,{\bf e}_y + {\bf e}_z\) is shown on the right, and I applied an ideal deformation by choosing an explicit flow map \((x_0,y_0,z_0)\to(x,y,z)\) given by a rotation \[\begin{align*} x &= x_0\cos\phi(z_0) - y_0\sin\phi(z_0)\\ y &= y_0\cos\phi(z_0) + x_0\sin\phi(z_0)\\ z &= z_0 \end{align*}\] where \(\phi(z) = \pi/2\,\exp(-25z^2).\) The advantage of an explicit flow map is that the deformed magnetic field is then given by the “Cauchy” solution \[ {\bf B}(x,y,z) = \frac{1}{\det(J)}J\,{\bf B}_0(x_0,y_0,z_0) \] with \(J_{ij} = \partial x_i/\partial x_{0j}\) being the Jacobian matrix. This avoids any the inevitable dissipation that you would have if the MHD equations were integrated numerically in time. The expression for \({\bf j}\) is more complicated (cf. Craig & Sneyd, 1986) but is easy to compute using sympy.

Note that I chose the initial condition so as to break the symmetry: if I take \({\bf B}_0={\bf e}_z\) then \(\lambda^*\) remains zero for all field lines.