Force-free fields: non-uniqueness and non-existence’

Illustrating the conceptual difficulties of force-free extrapolation.

Nonlinear force-free equilibria satisfy \(\boldsymbol{j} = \alpha\boldsymbol{B}\) with \(\alpha\) a non-trivial function of position. The fact that \(\alpha\) has to be constant along each magnetic field line makes the system “integrable”, limiting the topological complexity of these fields. However, because the governing equation \((\nabla\times\boldsymbol{B})\times\boldsymbol{B}=\boldsymbol{0}\) is nonlinear, when computing force-free extrapolations it is difficult to know what boundary conditions will give a well-posed problem.

In this post, I have collected two analytical “counter-examples” to show explicitly that the solutions can be non-unique and even non-existent for magnetic field boundary conditions such as solar magnetograms. These facts are well-known but I can’t find anywhere in the literature where they are explicitly demonstrated. For simplicity, we will use Cartesian coordinates where the solar photosphere is represented by the infinite plane \(y=0\) and the corona where we want to find a force-free field is the half-space \(y>0.\)

Example of non-uniqueness

The nicest example I have found originates in Low (1977) and is discussed on p352 of Schindler’s book. It is a solution of the (pressureless) Grad-Shafranov equation for a magnetic field \(\boldsymbol{B} = \nabla\times(A(x,y)\boldsymbol{e}_z) + B_z(A)\boldsymbol{e}_z,\) where the out-of-plane component is chosen to be \(B_z(A) = \sqrt{\lambda}\mathrm{e}^{-A}.\) This turns Grad-Shafranov into the Liouville equation \(\nabla^2A = \lambda\mathrm{e}^{-2A},\) so that solutions can be constructed analytically. We consider the particular pair of solutions \[ A = \ln\big(1 + x^2 + y^2 - 2h_\pm y\big), \qquad h_\pm = \pm\sqrt{1 - \lambda/4}, \] where \(\lambda < 4.\) These two solutions have different topology, corresponding to an arcade for \(h_-\) and a “flux rope” for \(h_+,\) respectively. (When \(\lambda=0\) the arcade solution becomes a potential arcade and the flux rope solution becomes a line current singularity surrounded by current free field.) Here is an illustration of the two solutions:

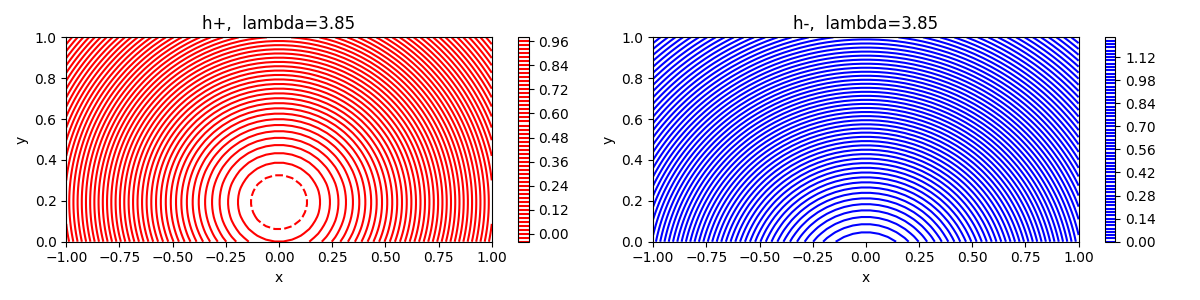
From my point of view here, the interesting thing is to look at the photospheric boundary conditions of these two solutions. The magnetic field on \(y=0\) is \[ \boldsymbol{B}(x,0) = \frac{-2h_\pm}{1+x^2}\boldsymbol{e}_x - \frac{2x}{1+x^2}\boldsymbol{e}_y + \frac{\sqrt{\lambda}}{1+x^2}\boldsymbol{e}_z, \] showing that they both have the same vertical field \(B_y(x,0).\) Incidentally, this vertical field doesn’t depend on \(\lambda,\) so you can generate a whole sequence of fields with the same normal-component on the boundary, ranging from potential with \(\lambda=0\) to force-free.

Notice that the \(h_+\) and \(h_-\) fields for the same \(\lambda\) also share the same \(B_z(x,0)\) distribution, though their \(B_x(x,0)\) components differ in sign. So far, I haven’t found an explicit example of two force-free fields that have exactly the same \(\boldsymbol{B}\) in the photosphere for all three components – i.e., the same vector magnetogram. To me, whether this is possible is still an open question.

Example of non-existence

It is known that not all vector magnetograms \(\boldsymbol{B}\) are compatible with a force-free extrapolation (for any \(\alpha\)) – for example, this is mentioned in the Living Reviews article by Wiegelmann and Sakurai. This is important when working with observed vector magnetogram data, meaning that they must be pre-processed for compatibility with the force-free assumption. Here, I will show how to prove this non-existence explicitly. The idea is to use the Virial Theorem (originally introduced in the context of MHD by Chandrasekhar, I think).

To derive the Virial Theorem, we start by writing \(\boldsymbol{j}\times\boldsymbol{B}\) as the divergence of the Maxwell stress tensor, \[ \boldsymbol{j}\times\boldsymbol{B} = \nabla\cdot\left(\frac{B^2}{2\mu_0}\mathbb{I} - \frac{\boldsymbol{B}\boldsymbol{B}}{\mu_0} \right). \] Setting this equal to zero, dotting with the position vector \(\boldsymbol{r},\) and integrating, leads after some algebra to \[ \int_V\frac{B^2}{2\mu_0}\,\mathrm{d}V = \oint_{\partial V}\left(\frac{B^2}{2\mu_0}\boldsymbol{r} - \frac{\boldsymbol{r}\cdot\boldsymbol{B}}{\mu_0}\boldsymbol{B} \right)\cdot\mathrm{d}\boldsymbol{S} \qquad (\dagger), \] where \(V\) is the coronal volume and $V $is the photospheric boundary (we assume that the solution decays at infinity).

The neat thing about the Virial Theorem \((\dagger)\) is that the energy of any force-free field is given purely by a boundary integral, if you know all three components of \(\boldsymbol{B}\) on the boundary. To prove that a force-free field cannot exist for some particular boundary map \(\boldsymbol{B}(x,0,z)\) on \(y=0\) (we consider the Cartesian case for simplicity), note that the lowest-energy magnetic field (that decays at infinity) is the potential extrapolation that matches the given normal component \(B_y(x,0,z).\) Call the energy of this potential field \(E_p.\) If we can find a distribution of \(B_x(x,0,z)\) and \(B_z(x,0,z)\) where \((\dagger)\) gives a lower energy than \(E_p,\) then we have a contradiction meaning that such a field cannot exist.

Initially, I tried to use the Low (1977) solution above to construct an example of this. But I think the potential field solution in that case actually has unbounded energy, so it’s a bit of a dodgy example. A better one is to take a submerged 3D dipole, \[ \boldsymbol{B} = \frac{3\boldsymbol{r}(\boldsymbol{m}\times\boldsymbol{r}) - r^2\boldsymbol{m}}{r^5}, \qquad \boldsymbol{m}=\boldsymbol{e}_x, \qquad \boldsymbol{r}=x\boldsymbol{e}_x + (y+1)\boldsymbol{e}_y + z\boldsymbol{e}_z. \] On the photosphere, this potential field has \[ B_x = \frac{2x^2-z^2-1}{(x^2 + z^2 + 1)^{5/2}}, \quad B_y=\frac{3x}{(x^2 + z^2 + 1)^{5/2}}, \quad B_z = \frac{3xz}{(x^2 + z^2 + 1)^{5/2}}. \] Using \((\dagger),\) with the help of Wolfram Alpha, I calculate the energy in the half-space \(y>0\) to be \[ E_p = \frac{\pi}{8\mu_0}. \] Now if I simply change the sign of \(B_z(x,0,z),\) I get a different vector map whose energy according to \((\dagger)\) is \[ E=-\frac{\pi}{16\mu_0} < E_p. \] This indeed contradicts the fact that the potential field is the minimum-energy field with that distribution of \(B_y(x,0,z),\) so I conclude that this vector map permits no force-free extrapolation. In fact, I didn’t need to bother with the potential field here, as a negative energy is always impossible!

Edit

Jean-Jacques Aly subsequently pointed out to me a simpler proof of non-existence that doesn’t use the Virial Theorem. The subject is discussed in his 1989 Solar Physics paper. His argument goes as follows. A force-free field satisfies \(\nabla\cdot\left(\frac{B^2}{2\mu_0}\mathbb{I} - \frac{\boldsymbol{B}\boldsymbol{B}}{\mu_0} \right) = \boldsymbol{0},\) so integrating over \(V,\) using the Divergence Theorem, and taking the \(x\)-component shows that any force-free field must satisfy the integral relation \[ \int_{y=0}B_xB_y\,\mathrm{d}S = 0. \] It is clear that you can readily find examples of fields for which this is violated. Jean-Jacques suggests considering the alternative boundary condition \(\boldsymbol{B'}(y=0) = \boldsymbol{B}(y=0) + k B_y(y=0)\boldsymbol{e}_x,\) where \(k\) is some constant. Then \[ \int_{y=0}B'_xB'_y\,\mathrm{d}S = k\int_{y=0}B_y^2\,\mathrm{d}S, \] so \(\boldsymbol{B}'\) has no force-free extrapolation for any \(k>0.\) In fact, since \(k\) can be made arbitrarily small, we can jump from existence to non-existence by an arbitrarily small change in the boundary conditions!

This argument also readily extends to the spherical case if we take the \(\phi\)-component of the integral relation to get \[ \int_{S}B_rB_\phi\,\mathrm{d}S=0 \] on the spherical surface.