$$ \def\ab{\boldsymbol{a}} \def\bb{\boldsymbol{b}} \def\cb{\boldsymbol{c}} \def\db{\boldsymbol{d}} \def\eb{\boldsymbol{e}} \def\fb{\boldsymbol{f}} \def\gb{\boldsymbol{g}} \def\hb{\boldsymbol{h}} \def\kb{\boldsymbol{k}} \def\nb{\boldsymbol{n}} \def\pb{\boldsymbol{p}} \def\qb{\boldsymbol{q}} \def\rb{\boldsymbol{r}} \def\tb{\boldsymbol{t}} \def\ub{\boldsymbol{u}} \def\vb{\boldsymbol{v}} \def\xb{\boldsymbol{x}} \def\yb{\boldsymbol{y}} \def\zb{\boldsymbol{z}} \def\Ab{\boldsymbol{A}} \def\Bb{\boldsymbol{B}} \def\Eb{\boldsymbol{E}} \def\Fb{\boldsymbol{F}} \def\Jb{\boldsymbol{J}} \def\Ub{\boldsymbol{U}} \def\xib{\boldsymbol{\xi}} \def\evx{\boldsymbol{e}_x} \def\evy{\boldsymbol{e}_y} \def\evz{\boldsymbol{e}_z} \def\evr{\boldsymbol{e}_r} \def\evt{\boldsymbol{e}_\theta} \def\evp{\boldsymbol{e}_r} \def\evf{\boldsymbol{e}_\phi} \def\evb{\boldsymbol{e}_\parallel} \def\omb{\boldsymbol{\omega}} \def\dA{\;\mathrm{d}\Ab} \def\dS{\;\mathrm{d}\boldsymbol{S}} \def\dV{\;\mathrm{d}V} \def\dl{\mathrm{d}\boldsymbol{l}} \def\bfzero{\boldsymbol{0}} \def\Rey{\mathrm{Re}} \def\Real{\mathbb{R}} \def\grad{\boldsymbol\nabla} \newcommand{\dds}[1]{\frac{\mathrm{d}{#1}}{\mathrm{d}s}} \newcommand{\ddy}[2]{\frac{\partial{#1}}{\partial{#2}}} \newcommand{\ddt}[1]{\frac{\mathrm{d}{#1}}{\mathrm{d}t}} \newcommand{\DDt}[1]{\frac{\mathrm{D}{#1}}{\mathrm{D}t}} $$
Surface flux transport
The surface flux transport (SFT) model has been central to much of my work: both providing an evolving lower boundary condition for coronal models, and as an observational tool to probe the solar dynamo.
Example. This video shows a classical SFT model (top) where active regions are modelled by idealised magnetic regions, compared to real synoptic magnetogram observations (bottom). Each frame corresponds to one solar rotation (about 27 days).
Introduction
In the classical SFT model [1], large-scale mean magnetic field \(B_r\) on the solar surface evolves as a passive scalar field, \[ \ddy{B_r}{t} + \nabla_h\cdot(\textcolor{blue}{\ub_h} B_r) = \textcolor{red}{\eta_0}\nabla_h^2 B_r + S. \] The surface velocity \(\textcolor{blue}{\ub_h}\) includes differential rotation and meridional flow, while the diffusivity \(\textcolor{red}{\eta_0}\) models the net effect of unresolved (supergranular) convective motions in spreading out and cancelling the magnetic flux. The source term \(S\) is critical and represents the emergence of new active regions – it is a function of space and time, and much of the art of SFT model is how to choose this term to match observations.
For a detailed overview of the SFT model, see our review [2].
Selected papers
[3] – my very first research paper, during my PhD. The problem was to develop an SFT model that assimilates individual observed active regions but maintains a reasonable match to the overall magnetic field pattern over a 6-month period. This was needed as the lower boundary driver for our 3D magneto-frictional model.
[4] – a side project during my PhD, during two summer visits to Montana State University. Not SFT but a flux transport dynamo model for the solar interior. The paper was quite influential because it resolved a major discrepancy between two dynamo-based predictions of solar cycle amplitude that had been published during SC23. I simulated both within the same (2D) model and identified a fundamental difference in memory between “advection-dominated” and “diffusion-dominated” regimes. Subsequent observations have vindicated our proposal that the diffusion-dominated model was better.
[5] – with Andrés Muñoz-Jaramillo, this was the first 3D implementation of the kinematic flux transport dynamo model, which essentially extends the SFT model to the solar interior. Unlike earlier 2D models (e.g. [4]), this accounts consistently for magnetic flux conservation during the emergence process. Later, my PhD student Tim Whitbread used the model [6] to show that active regions must rapidly disconnect from their roots at the base of the convection zone, for the surface field to match observations.
[7] – Tim Whitbread used a genetic algorithm to with four cycles of magnetogram data do a more thorough optimization of the SFT model parameters than previously. He found an optimal meridional flow profile that matched (independent) observations. Tim’s work also hinted at the importance of active region shapes (later developed by [8]). His second paper [9] looked at the contribution of individual active regions to the global dipole, finding that the top \(10\%\) of contributors tend to define sudden large variations in the dipole, including the weak polar field at the end of SC23.
[10] – a neat paper using analytical approximation to predict the ultimate dipole contribution of each active region in the SFT model. To contribute to the global dipole, they must emerge near enough to the equator, as determined by the dimensionless number \(\textcolor{red}{\eta_0}(R_\odot^2\textcolor{blue}{\Delta_u})^{-1}\), where \(\textcolor{blue}{\Delta_u=R_\odot^{-1}u_\theta'(\pi/2)}\) is the “flow divergence” at the equator. More details in [2].
[8] – I used HMI/SHARPs magnetogram data for SC24 to show that approximating the real shapes of active regions by idealised magnetic bipoles (commonly done in previous models) has the effect of overestimating the end-of-cycle axial magnetic dipole by \(24\%\). I was honoured that this paper was awarded the 2021 Kees de Jager Prize.
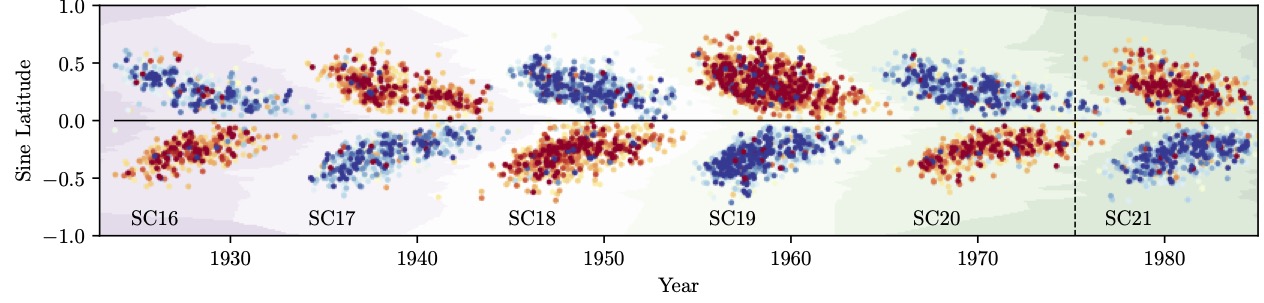
[11] – we used digitised historical observations from Mount Wilson Observatory to construct a “best-fit” SFT model for the years 1923-1985. Active regions are determined from Ca II K “plages”, with polarities informed by sunspot magnetic measurements. The paper used the model to show that there is more evidence for latitude quenching than tilt quenching in regulating the solar dynamo. See also a video of my seminar at HAO. The butterfly diagram below shows the individual active regions derived for this model, coloured by the flux of their leading polarity.
Software
sftdata – an older 2D SFT code in MATLAB, as described in [12] and used by [7]. The active regions are extracted from synoptic magnetograms in .fits format.
sharps-bmrs – Python code for automated extraction of magnetic regions from the HMI/SHARPs database, as described and used by [8] and subsequently to drive magneto-frictional models, e.g. [13].
sft-historical – Python+Fortran code for SFT modelling driven by active regions from historical data, as described in [11].
Datasets
- Bipolar magnetic regions determined from NSO synoptic carrington maps (hosted by Solar Dynamo Dataverse). The method was originally described by [3].
- Active region dipole moments determined from NSO carrington maps (hosted by Solar Dynamo Dataverse). These data do not assume particular bipolar shapes for active regions and were determined by my student Tim Whitbread for (originally) the paper [9].
- Bipolar magnetic regions and dipole moments determined from HMI/SHARPs data (hosted by Harvard Dataverse). This is a ready-produced file using my automated sharps-bmrs code above, with the parameter values used in the paper [8]. This database includes not only the dipole moments at time of observation but also predicted end-of-cycle dipole moments using surface flux transport. See the paper for details.
- Historical magnetic regions from Ca II K synoptic maps (hosted by Durham University Collections). This is a repository of the ensemble data created for the paper [11].