$$ \def\ab{\boldsymbol{a}} \def\bb{\boldsymbol{b}} \def\cb{\boldsymbol{c}} \def\db{\boldsymbol{d}} \def\eb{\boldsymbol{e}} \def\fb{\boldsymbol{f}} \def\gb{\boldsymbol{g}} \def\hb{\boldsymbol{h}} \def\kb{\boldsymbol{k}} \def\nb{\boldsymbol{n}} \def\pb{\boldsymbol{p}} \def\qb{\boldsymbol{q}} \def\rb{\boldsymbol{r}} \def\tb{\boldsymbol{t}} \def\ub{\boldsymbol{u}} \def\vb{\boldsymbol{v}} \def\xb{\boldsymbol{x}} \def\yb{\boldsymbol{y}} \def\zb{\boldsymbol{z}} \def\Ab{\boldsymbol{A}} \def\Bb{\boldsymbol{B}} \def\Eb{\boldsymbol{E}} \def\Fb{\boldsymbol{F}} \def\Jb{\boldsymbol{J}} \def\Ub{\boldsymbol{U}} \def\xib{\boldsymbol{\xi}} \def\evx{\boldsymbol{e}_x} \def\evy{\boldsymbol{e}_y} \def\evz{\boldsymbol{e}_z} \def\evr{\boldsymbol{e}_r} \def\evt{\boldsymbol{e}_\theta} \def\evp{\boldsymbol{e}_r} \def\evf{\boldsymbol{e}_\phi} \def\evb{\boldsymbol{e}_\parallel} \def\omb{\boldsymbol{\omega}} \def\dA{\;\mathrm{d}\Ab} \def\dS{\;\mathrm{d}\boldsymbol{S}} \def\dV{\;\mathrm{d}V} \def\dl{\mathrm{d}\boldsymbol{l}} \def\bfzero{\boldsymbol{0}} \def\Rey{\mathrm{Re}} \def\Real{\mathbb{R}} \def\grad{\boldsymbol\nabla} \newcommand{\dds}[1]{\frac{\mathrm{d}{#1}}{\mathrm{d}s}} \newcommand{\ddy}[2]{\frac{\partial{#1}}{\partial{#2}}} \newcommand{\ddt}[1]{\frac{\mathrm{d}{#1}}{\mathrm{d}t}} \newcommand{\DDt}[1]{\frac{\mathrm{D}{#1}}{\mathrm{D}t}} $$
Magnetic braids
I have used magnetic braids as a testbed for studying topological constraints on resistive plasma relaxation. This work arose from my postdoc at the University of Dundee, and has been in collaboration with Gunnar Hornig (Dundee), Alexander Russell (St Andrews), and Chris Prior (Durham). It is fundamental research, but strongly motivated by coronal loops in the solar atmosphere.
Introduction
A magnetic braid is our name for a single magnetic flux tube – for example, a magnetic field \(\Bb(x,y,z)\) between two boundaries \(0<z<1\) with a “guide field” \(B_z>0\).

In one sense a magnetic braid has no magnetic topology, having no null points (where \(\Bb=\bfzero\)) and consequently no magnetic skeleton. But if we line-tie the field line footpoints like those of a coronal loop, then only certain end states are reachable by ideal (flux-conserving) evolution, while others require magnetic reconnection so as to change the footpoint connectivity.
For example, the infamous Parker problem asks whether an arbitrary initial \(\Bb\) can always relax to a smooth force-free equilibrium without reconnection?
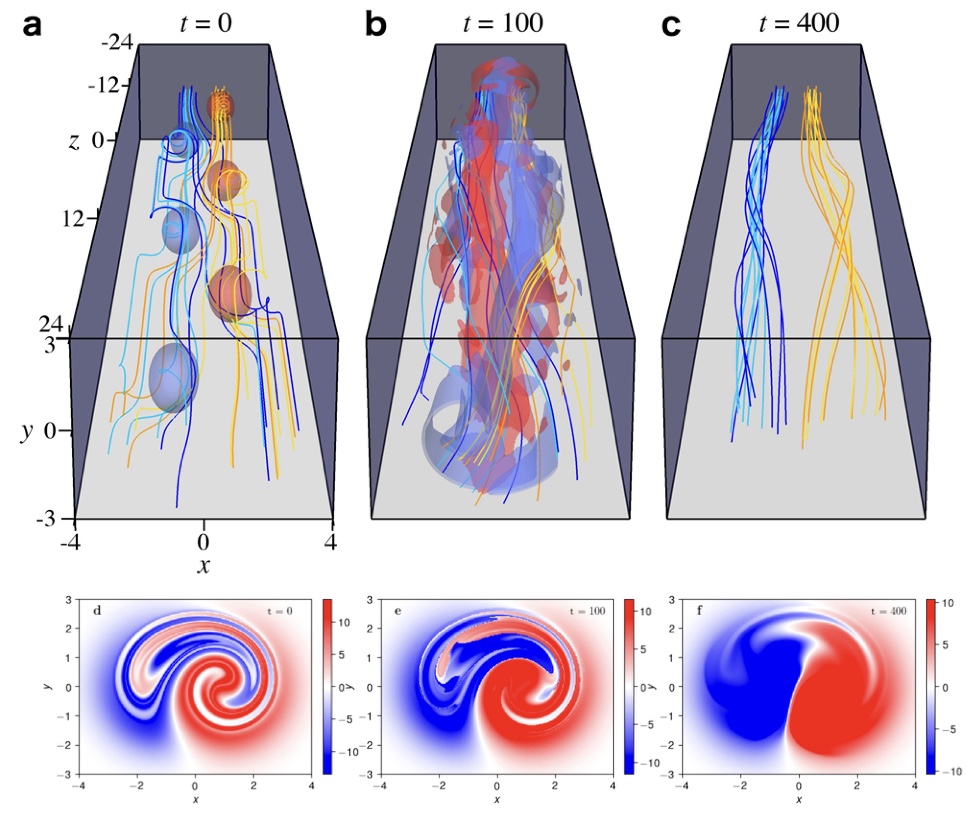
Even if reconnection is permitted, the system may still reach only a local energy minimum on the dynamical timescale of interest. Much of our research has focused on this problem of resistive relaxation.
Selected papers
[2] – we identified a robust new topological invariant that explains why certain numerical simulations of magnetic braids could not relax to the expected energy minimum: the topological degree. This applies to any resistive evolution where the reconnection is localised (in the transverse direction), and \(\Bb\) has a continuous field line mapping from \(z=0\) to \(z=1\). For a better overview of the mathematics, see [3]. If the boundary conditions are periodic, you can sometimes find an independent invariant of the iterated map [4].
[5] – I like this paper because it achieved what we originally set out to do in my postdoc project at Dundee: partition the magnetic flux in a magnetic braid so as to define a reconnection rate. It’s a fun problem because the flux surfaces that you would have in a 2-d magnetic field break down into heteroclinic tangles. But the field line helicity (aka. topological flux function) behaves in certain ways as the analogue of a classical 2-d flux function.
[6] – we proved that the field line mapping of a magnetic braid is uniquely classified by its field line helicity (aka. topological flux function). Probably my deepest mathematical result to date. See [6] for a more polished proof using differential forms. The key idea is that the field line helicity is the action in a hamiltonian system whose trajectories are the magnetic field lines.
[7] – this is a theoretical paper where we show how to derive an evolution equation for field line helicity during resistive evolution of a magnetic braid. See also my lecture notes. In localised reconnection, our analysis predicted that rearrangement of field line helicity should be much more efficient than its dissipation.
[1] – this paper verifies the previous prediction using numerical MHD simulations of the turbulent relaxation of a magnetic braid. This is important because it refines the classical Taylor theory, the final relaxed state is predicted by energy minimisation based purely on conservation of total helicity, \(\int_V\Ab\cdot\Bb\,dV\). Instead, we find for magnetic braids that – to leading order – the pattern is rearranged by reconnection but not destroyed. For an overview, see also my poster.
[8] – with Chris Prior, we extended the unique classification result [6] to (i) more general tubular domains, and (ii) non-solenoidal vector fields, using the related field line winding instead of field line helicity.
[9] – this was the outcome of a Leverhulme Trust project where postdoc Long Chen computed the optimally unstirred state of a passive scalar. We found that the best way to avoid dissipation was a viscous magnetic relaxation method, treating the contours as 2-d magnetic field lines. This work was motivated by the dominant behaviour of field line helicity in the relaxation of magnetic braids, and whether we could “predict” the final pattern without following the full 3-d dynamics.