Convex Analysis

The notion of convexity is a notion of great importance in the field of modern analysis, one whose reach encompasses both sets and functions. It lies at the cusp of Geometry, Topology and Analysis and at times acts as a bridge between these fields, helping us explore many problems from different viewpoints.

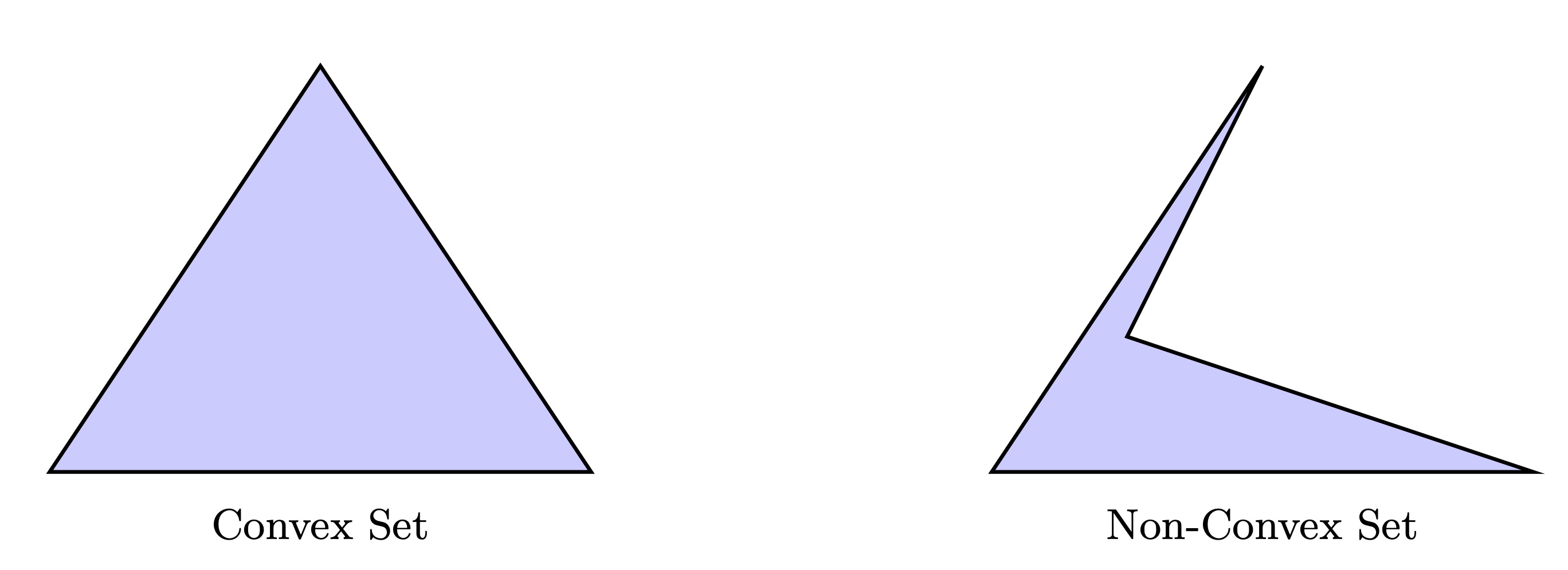
A set \(C\) in \(\mathbb{R}^n\) is called a convex set if for any \(\theta \in [0,1]\) and any \(x,y\in C\) we have that $$\theta x + (1-\theta)y \in C.$$ In other words -- if \(x,y\in C\) then the segment that connects between them lies entirely in \(C\).

A function \(f\) from a convex set \(C\) to \(\mathbb{R}\) is called convex on \(C\) if for any \(\theta \in [0,1]\) and any \(x,y\in C\) we have that $$f\left(\theta x + (1-\theta)y\right) \leq \theta f(x) + (1-\theta)f(y).$$ While this might look daunting, when \(C\) is an interval the above it is nothing more than saying that the straight line connecting the points \(\left(x,f(x) \right)\) and \(\left(y,f(y) \right)\) lies above the graph of the function \(f\) between \(x\) and \(y\).

Convex sets and functions enjoy an abundance of properties and play an important roles in many topics -- both in theory and applications. For instance:

• Convex sets have many "good" topological properties
• Convex sats are essential in many optimisation problems (such as linear optimisation).
• Convex functions are continuous and almost everywhere differentiable.
• The graph of a convex function on \(\mathbb{R}\) lies above their tangent line.
• A local minimum of a convex function is, in fact, a global minimum of the function.

Our goal in this project will be to explore the theory of convex sets and functions, and the connection between them. Once established, you will be able to explore additional topics such as:

• Convexity in general normed spaces.
• Separation properties of convex sets (Hahn-Banach Theorem).
• Conjugate functions (Legendre transform) and Fenchel duality.
• Differentiability of convex functions.
• Applications to functional inequalities (Young's inequality, Hölder's inequality, Jensen's inequality, and the Brunn–Minkowski inequality are but a few examples).

Prerequisites : Analysis I (essential), Linear Algebra I and Complex Analysis II.

Potential co-requisite (not mandatory but helpful): Analysis III.

• R. T. Rockafellar: Convex Analysis.
• P. M. Gruber, J. M. Wills: Convexity and its applications.
• J. M. Borwein & J. D. Vanderwerff: Convex Functions: Constructions, Characterization and Counterexamples.
• A. V. Arutyunov & V. Obukhovskii: Convex and Set-Valued Analysis.
• B. Simon: Convexity - An Analytic Viewpoint.