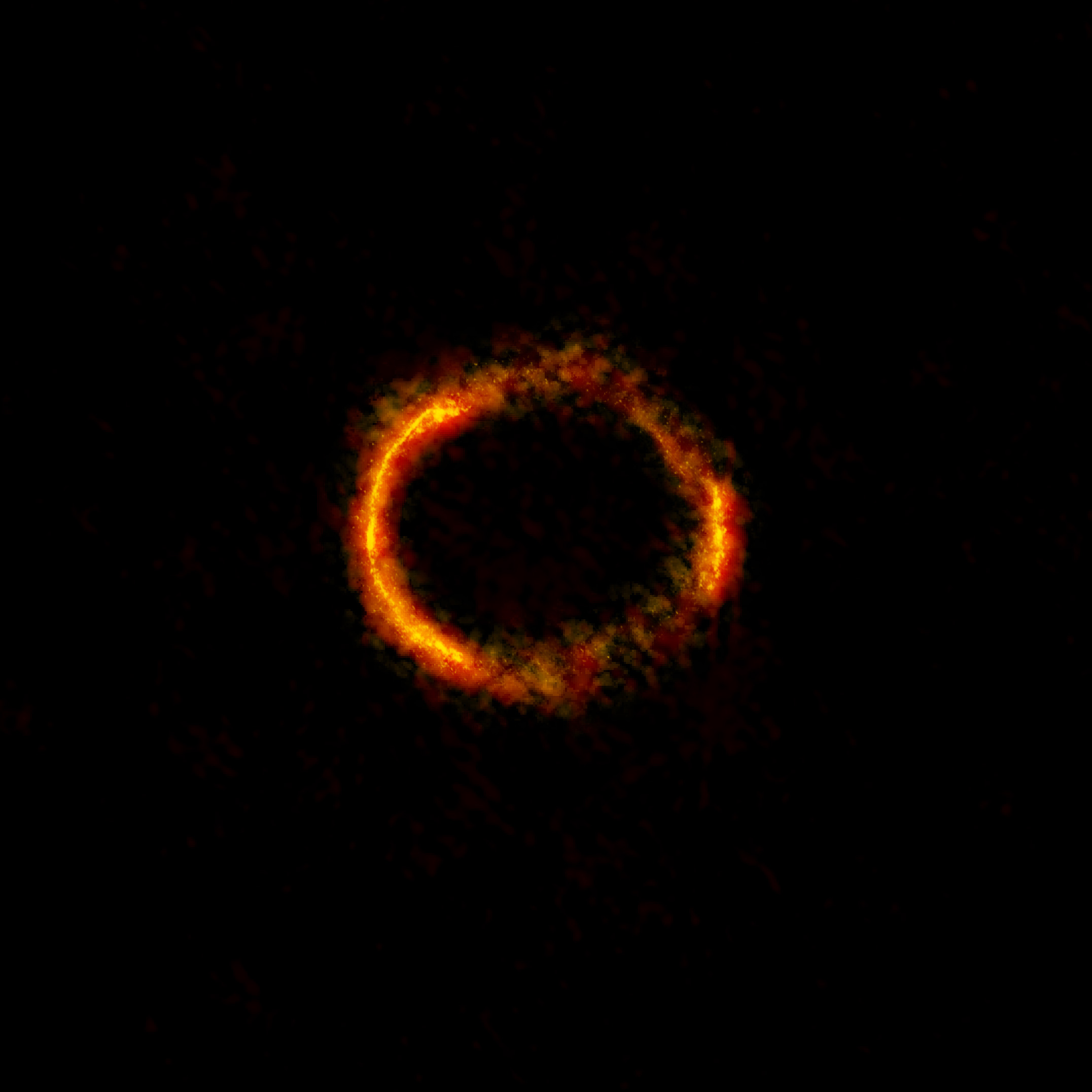
Description. Einstein's theory of General Relativity (GR) models gravity in terms of curved space-time. One of its predictions is that gravity bends light, and this was famously confirmed in 1919, in observations of light bending around the edge of the Sun during a solar eclipse. In that case, the amount of bending was small. But stronger gravitational fields, such as those near black holes, can cause light-rays to deviate very considerably.

The project will begin by taking the equations describing light-rays passing near a compact massive object such as a star or a black hole, and investigating how the image of a source beyond that object gets deformed. An additional aspect might be to consider black holes which are rapidly-spinning, resulting in some special features, since the rotating mass drags space around with it.

The remainder of the project will be to give a concise account of the relevant parts of GR and its geometrical framework, and to derive the equations for light-rays which you used earlier.

Prerequisites: Familiarity with the mathematics of space-time, in particular Special Relativity, via the module SREM II or its Physics equivalent.

Photograph of an Einstein ring: the lensed image of a distant galaxy.