Description
Some field theories have wave-like solutions which look like localised 'lumps' of energy. In one spatial dimension, these are often kinks, field configurations which interpolate between two different values at plus and minus infinity. Physicists and mathematicians have long been interested in the properties of these solutions, which keep their form over time and scatter against each other very much like particles. The classic examples are the kinks of the sine-Gordon model, which are discussed in the solitons course. However these are rather special in that they retain their shapes exactly under scattering, a fact which is related to a property called integrability. More recently researchers have realised that a much richer structure can be found in the scattering of kinks in non-integrable field theories. Numerical simulations showed fascinating, fractal-like structures of bounces and resonances, which are now being understood analytically.
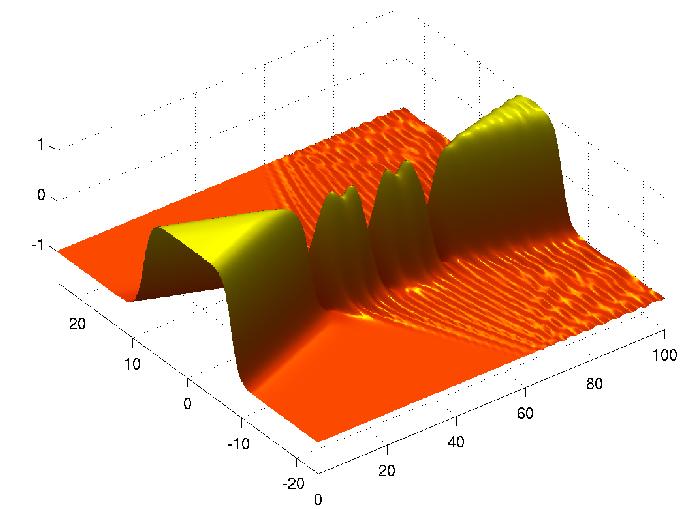
The aim of this project is to investigate kink solutions of one-dimensional field theories, and how they interact with each other and with obstacles and boundaries. There would also the option to look at some very-recent work showing that similar phenomena can occur in higher dimensions. The project has an analytical side, understanding for example how kinks can influence each other when far apart, but there is also plenty of scope for numerical experiments using Python, and the possibility to explore real-world applications of these effects. It would be useful to have taken the solitons course.
Resources
- The picture above is from this article. This work was also described in a short 'journal club' item in Nature, and in the review section of this article. A survey article covering more-recent developments is here.
- Chapters 5 and 6 of Physics of Solitons by Dauxois and Peyrard will get you started on how kinks can wobble; and chapter 5 of Topological solitons by Manton and Sutcliffe has further discussion of kinks in the φ4 and sine-Gordon theories.
- There are also many journal articles - some written by people in Durham - relevant to this project. We'll discuss these as the project develops but please feel free ask for a preview if you're interested in chosing this topic.