Description
This project begins with the following problem: you observe a pair of tracks in the snow, made some time before by the front and rear wheels of a bicycle:
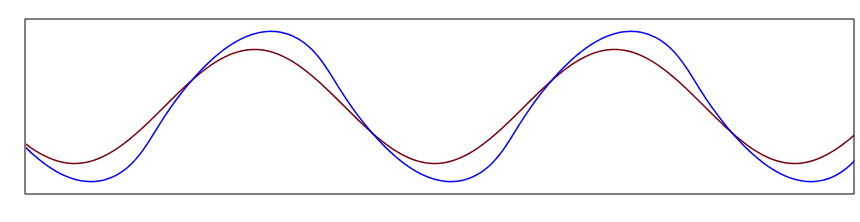
The question is, on the basis of the shape of these tracks alone, can you tell which way the bicycle was travelling - left to right, or right to left? This was famously posed, and then answered incorrectly, in the Sherlock Holmes short story "The Adventure of the Priory School".
The key to the correct answer is the fact that it is the front wheel that does the steering, while the rear wheel always points along the frame towards the front wheel. This tells you something about the tangent line to the rear-wheel track: at a fixed distance in the forward direction, it must hit the front-wheel track. Before scrolling down, you might try to use this observation to figure out which of the two tracks above must correspond to the front wheel, and then, given that, which direction the bicycle was travelling.
This is just the first of a whole sequence of questions with unexpected links to other areas of mathematics such as soliton theory and elliptic functions, some of which you could explore in this project. For example, might there be 'ambiguous' pairs of tracks for which neither you nor even Sherlock Holmes could figure out the bicycle's direction of travel? Straight lines and circles are obvious examples, but it turns out that there are more, and that these provide solutions to another famous problem: are there any non-circular cross-sections for a cylindrical body which would allow it to float in any orientation?
Prerequisites
Some familiarity with ordinary differential equations will help, as will a willingness to make numerical explorations for yourself using a computer.
Resources
- The Sherlock Holmes story can be found here, and its mathematical failings are discussed in, for example, the short article "Sherlock Holmes and the Bicycle tracks".
- For some animations of ambiguous tracks, see here.
- The bicycle track problem has been discussed in a number of articles by Tabachnikov and collaborators. See for example here and here.
- Links with the floating-body problem are described here.
The answer to the problem at the top of the page:
For the tracks plotted above, the blue curve must be the front wheel, and furthermore the direction of travel is from left to right:
