AMV II Epiphany Exercises 2023

1 Unit 1. Non Cartesian systems.

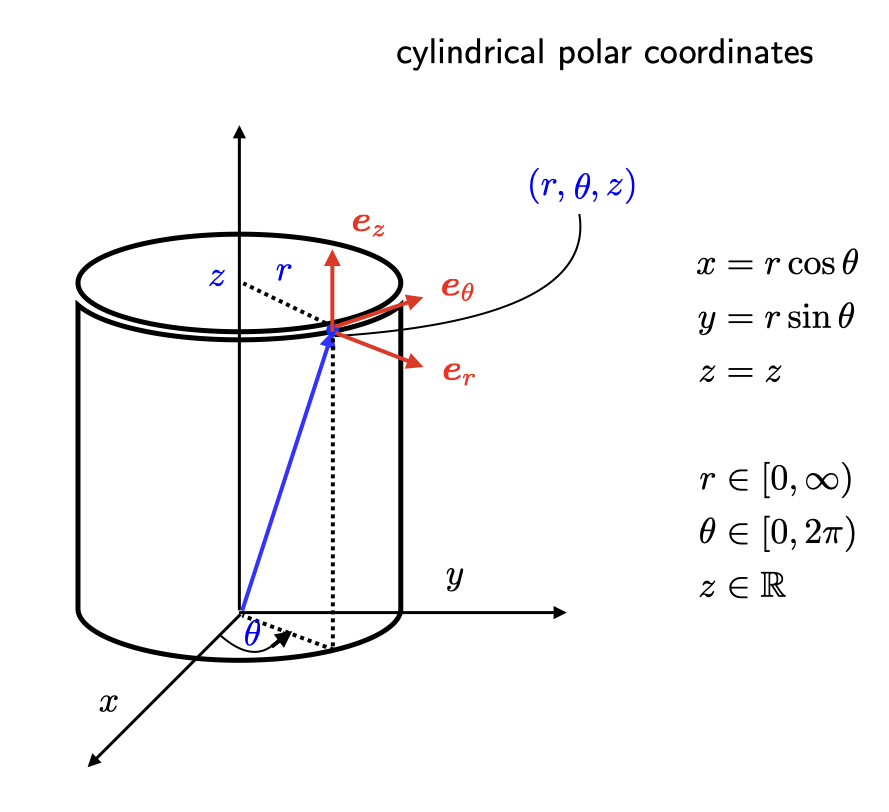
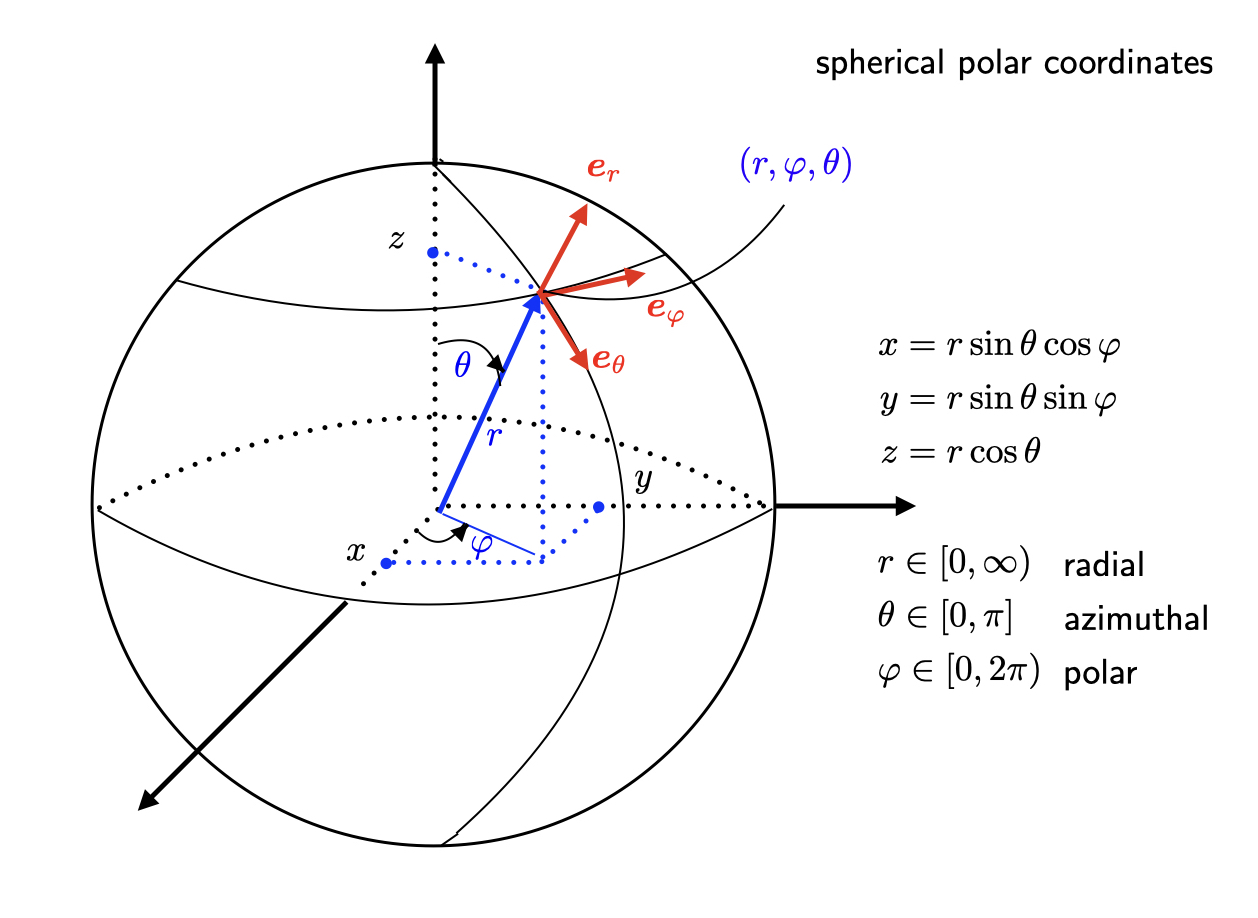
You are not asked to memorise the formulas giving the cylindrical polar and spherical polar coordinates in AMV II. In an exam paper, they would be given to you if necessary. It would be good if you could remember the change to polar coordinates in two dimensions though.

Polar coordinates: $x=r\cos \theta ,y=r\sin \theta$ with $r\in [0,\mathrm{\infty })$, $\theta \in [0,2\pi )$.
Cylindrical polar coordinates: $x=r\cos \theta ,y=r\sin \theta ,z=z$ with $r\in [0,\mathrm{\infty })$, $\theta \in [0,2\pi )$ and $z\in ℝ$.
Spherical polar coordinates: $x=r\sin \theta \cos \phi ,y=r\sin \theta \sin \phi ,z=r\cos \theta$ with $r\in [0,\mathrm{\infty })$, $\theta \in [0,\pi ]$, $\phi \in [0,2\pi )$.

Figure 1: Cylindrical polar and spherical polar coordinates.

1.1 Double and triple integrals in orthogonal curvilinear coordinates

Exercise 1.1

The following equations are given in spherical polar coordinates. Interpret each of them geometrically.

$$(a)r\sin \theta =1,(b)r\cos \theta =1,(c)r=\cos \theta ,(d)(\mathrm{𝐓𝐔𝐓𝟏})\cos \theta =-\frac{\sqrt{2}}{2}.$$

Exercise 1.2

• Find an equation in spherical polar coordinates for the sphere of equation

  $$x^2+y^2+{(z-R)}^2=R^2,R\mathrm{real}\mathrm{constant}.$$

• Express the upper-half of the ball $x^2+y^2+{(z-R)}^2\le R^2$ by giving the relevant ranges of the three spherical polar coordinates $r,\theta ,\phi$.

Exercise 1.3 (TUT 1)

By expressing both the integrand and the surface element in spherical polar coordinates, evaluate the surface integral

$$I=\underset{\mathrm{\Sigma }}{\iint }\frac{x^2}{x^2+y^2}𝑑S$$

where $d\mathit{}S$ is an infinitesimal surface element on the surface $\mathrm{\Sigma }$ of equation $x^{\mathrm{2}}\mathrm{+}{y}^{\mathrm{2}}\mathrm{=}{z}^{\mathrm{2}}$, $\mathrm{0}\mathrm{\le }z\mathrm{\le }\mathrm{1}$.

Exercise 1.4

Use cylindrical polar coordinates to calculate

$$I=\underset{R}{\iiint }(x^2+y^2)𝑑x𝑑y𝑑z$$

for the region $R\mathrm{:}\mathrm{-}\mathrm{2}\mathrm{\le }x\mathrm{\le }\mathrm{2}\mathrm{,}\mathrm{-}\sqrt{\mathrm{4}\mathrm{-}{x}^{\mathrm{2}}}\mathrm{\le }y\mathrm{\le }\sqrt{\mathrm{4}\mathrm{-}{x}^{\mathrm{2}}}\mathrm{,}\mathrm{0}\mathrm{\le }z\mathrm{\le }\mathrm{4}\mathrm{-}{x}^{\mathrm{2}}\mathrm{-}{y}^{\mathrm{2}}$.

Exercise 1.5 (${}^{\ast }$Extension exercise)

Use cylindrical polar coordinates $x\mathrm{=}r\mathit{}\cos \mathit{}\theta \mathrm{,}y\mathrm{=}r\mathit{}\sin \mathit{}\theta \mathrm{,}z\mathrm{=}z$ to find the volume of the solid $B$ bounded above by the plane $z\mathrm{=}y$ and below by the paraboloid of equation $z\mathrm{=}{x}^{\mathrm{2}}\mathrm{+}{y}^{\mathrm{2}}$.

1.2 Differential operators in curvilinear coordinates

The convention here is that $\{{𝐞}_1,{𝐞}_2,{𝐞}_3\}$ form a right-handed basis in Cartesian coordinates, that is, ${𝐞}_i\times {𝐞}_j={ϵ}_{ijk}{𝐞}_k,i\in \{1,2,3\}$.

Exercise 1.6

Express the differential equation

$${\partial }_{t}U=\kappa {\mathbf{\nabla }}^{2}U$$

with $U$ a function of the coordinates $\mathrm{(}r\mathrm{,}\theta \mathrm{,}z\mathrm{,}t\mathrm{)}$ in cylindrical polar coordinates.The variable $t\mathrm{\in }\mathrm{R}$ is often labelling time in problems.

Exercise 1.7 (TUT 1)

Represent the vector $\mathrm{A}\mathrm{=}z\mathit{}{\mathrm{e}}_{\mathrm{1}}\mathrm{-}\mathrm{2}\mathit{}x\mathit{}{\mathrm{e}}_{\mathrm{2}}\mathrm{+}y\mathit{}{\mathrm{e}}_{\mathrm{3}}$ in cylindrical polar coordinates and state what $A_r\mathrm{,}{A}_{\phi }$ and $A_z$ are.

Exercise 1.8 (TUT 1)

Calculate $\mathrm{\nabla }\mathrm{\times }\mathrm{A}$ for $\mathrm{A}\mathit{}\mathrm{(}r\mathrm{,}\theta \mathrm{,}\phi \mathrm{)}\mathrm{=}r\mathit{}{\mathrm{e}}_{\theta }\mathrm{+}{\mathrm{e}}_{\phi }$ in spherical polar coordinates, with

$$x=r\sin \theta \cos \phi ,y=r\sin \theta \sin \phi ,z=r\cos \theta ,r\in [0,\mathrm{\infty }),\theta \in [0,\pi ),\phi \in [0,2\pi ).$$

You may use the formula

$\mathbf{\nabla }\times 𝐀$

$=h_r^{-1}{h}_{\theta }^{-1}{h}_{\phi }^{-1}\{h_r{𝐞}_r[{\partial }_{\theta }(A_{\phi }{h}_{\phi })-{\partial }_{\phi }(A_{\theta }{h}_{\theta })]-h_{\theta }{𝐞}_{\theta }[{\partial }_r(A_{\phi }{h}_{\phi })-{\partial }_{\phi }(A_r{h}_r)]$

$+h_{\phi }{𝐞}_{\phi }[{\partial }_r(A_{\theta }{h}_{\theta })-{\partial }_{\theta }(A_r{h}_r)]\},$

where $h_r\mathrm{,}{h}_{\theta }$ and $h_{\phi }$ are the scale factors for spherical polar coordinates.

Exercise 1.9 (${}^{\mathbf{\ast }}$Extension exercise)

Let the Cartesian coordinates $\mathrm{(}x\mathrm{,}y\mathrm{,}z\mathrm{)}$ of any point in ${\mathrm{R}}^{\mathrm{3}}$ be expressed as functions of $\mathrm{(}u\mathrm{,}v\mathrm{,}z\mathrm{)}$ so that

$$x=a\cosh u\cos v,y=a\sinh u\sin v,z=z,u\in [0,\mathrm{\infty }),v\in [0,2\pi ),z\in ℝ,$$

and $a$ a positive constant. We shall call the system with coordinates $\mathrm{(}u\mathrm{,}v\mathrm{,}z\mathrm{)}$ the $\mathrm{EC}$ system.

• Is the $\mathrm{𝐄𝐂}$ system orthogonal?

• Calculate the scale factors $h_u,h_v$ and $h_z$.

• Give the unit vectors ${𝐞}_u,{𝐞}_v,{𝐞}_z$ in the Cartesian basis.

• Calculate the gradient in the basis $\{{𝐞}_u,{𝐞}_v,{𝐞}_z\}$ of the $\mathrm{𝐄𝐂}$ system.

• Express ${𝐞}_1,{𝐞}_2$ and ${𝐞}_3$ in terms of ${𝐞}_u,{𝐞}_v$ and ${𝐞}_z$.

• Given that

  $${\partial }_u{𝐞}_v=\frac{\sin v\cos v}{{\sinh }^{2}u+{\sin }^{2}v}{𝐞}_u,{\partial }_v{𝐞}_v=-\frac{\sinh u\cosh u}{{\sinh }^{2}u+{\sin }^{2}v}{𝐞}_u,{\partial }_z{𝐞}_v=0,$$

  calculate the curl of the vector field $𝑨(u,v,z)=z^2{𝐞}_v$ (i.e. $\mathbf{\nabla }\times z^2{𝐞}_v$) in the $\mathrm{𝐄𝐂}$ system.

• Give the form of the Laplacian in this coordinate system.

Exercise 1.10 (GRAD 1)

• Write the curve $x^4=9(x^2-y^2)$ in polar coordinates. [2 marks]

• Test this curve for symmetries (you may decide to work from the equation in Cartesian or polar coordinates for this). [2 marks]

• Sketch the curve. [2 marks]

• Evaluate the area of the region in the xy-plane bounded by the curve. [4 marks]

Exercise 1.11 (GRAD 1)

• Calculate the Laplacian ${\nabla }^2𝐀$ for the vector field $𝐀={𝐞}_{𝐫}$ in cylindrical polar coordinates.                                                                                           [5 marks]

• Rework the same problem in Cartesian coordinates and show that the two results coincide (as they should). [5 marks]

2 Unit 2: Generalised functions

Exercise 2.1

Let $\mathrm{\Theta }$ be the unit step function defined on $\mathrm{R}$ as

Give a definition and sketch the following functions,

• $\mathrm{\Theta }(x-a)$ for $a\in {ℝ}^{+}$

• $\mathrm{\Theta }(x+a)$ for $a\in {ℝ}^{+}$

• $\mathrm{\Theta }(-x)$

• (TUT 2) $\mathrm{\Theta }(x)+\mathrm{\Theta }(-x)$

• $e^x\mathrm{\Theta }(x)$

Exercise 2.2

Given that, in the sense of distributions,

$${\mathrm{\Theta }}^{\prime }(x)=\frac{d\mathrm{\Theta }(x)}{dx}=\delta (x),\forall x\in ℝ,$$

calculate, for $a\mathrm{\in }\mathrm{R}$,

• (TUT 2) $\frac{d}{dx}\mathrm{\Theta }(ax)$

• $\frac{d}{dx}\mathrm{\Theta }(x^2-a)$

• $\frac{d}{dx}\mathrm{\Theta }(x-a)$

Exercise 2.3

By integrating both sides against an arbitrary test function $\psi \mathrm{\in }\mathrm{D}\mathit{}\mathrm{(}\mathrm{R}\mathrm{)}$, find the coefficients $A$ and $B$, and possibly the constant $C$ in the following generalised identities,

• (TUT 2) $x^3{\delta }^{\prime }(x-3)=B\delta (x-C)+D{\delta }^{\prime }(x-C)$.

• $x^2{\delta }^{(2)}(x)=A\delta (x)$,

• (TUT 2) $x^2\delta (x^3)=B\delta (x)$

where ${\delta }^{\mathrm{(}\mathrm{2}\mathrm{)}}\mathit{}\mathrm{(}x\mathrm{)}$ denotes the second derivative of the Dirac delta distribution.

Exercise 2.4

By integrating both sides against an arbitrary test function $\psi \mathrm{\in }\mathrm{D}\mathit{}\mathrm{(}\mathrm{R}\mathrm{)}$, find the coefficients $A\mathrm{,}B\mathrm{,}C\mathrm{,}D$ and $B_m\mathrm{,}m\mathrm{\in }\mathrm{\{}\mathrm{0}\mathrm{,}\mathrm{\dots }\mathrm{,}n\mathrm{\}}$ in the following generalised identities,

1. $x{\delta }^{(2)}(3x)=A{\delta }^{\prime }(x)$

2. $e^{-x}{\delta }^{(2)}(x)=B{\delta }^{(2)}(x)+C{\delta }^{\prime }(x)+D\delta (x)$.

3. $e^{-\lambda x}{\delta }^{(n)}(x)={\sum }_{m=0}^n{B}_m{\delta }^{(m)}(x)$, where $\lambda$ is a real constant.

Exercise 2.5

By integrating both sides against an arbitrary test function find the coefficients $A$ and $B$ in the following generalised function identity,

$$\delta (x^2-(\xi +\rho )x+\xi \rho )=A\delta (x-\xi )+B\delta (x-\rho ),$$

where $\xi$ and $\rho$ are constants, with $\xi \mathrm{\ne }\rho$. Justify your steps fully.

Exercise 2.6

Give an expression for the charge density function $\rho \mathit{}\mathrm{(}\mathrm{r}\mathrm{)}$ of a ring of charge Q and radius $a$ centred at the origin and lying in the $x\mathit{}y$-plane

• in cylindrical polar coordinates.

• in spherical polar coordinates.

Then use spherical polar coordinates to calculate the electric potential $\mathrm{\Phi }\mathit{}\mathrm{(}\mathrm{r}\mathrm{)}$ resulting from that ring distribution of charge at a point $\mathrm{r}\mathrm{=}z\mathit{}{\mathrm{e}}_{\mathrm{3}}$ on the $z$-axis,

$$\mathrm{\Phi }(𝐫):=\frac{1}{4\pi {ϵ}_0}{\int }_{{ℝ}^3}\frac{\rho ({𝐫}^{\prime })}{|𝐫-{𝐫}^{\prime }|}𝑑V^{\prime },$$

where ${ϵ}_{\mathrm{0}}$ is the vacuum permittivity constant and $d\mathit{}{V}^{\mathrm{\prime }}$ is the volume element expressed in the primed coordinates.

Exercise 2.7

• (TUT 2) Show that the generalised function $g(x)=c_1\delta (x)+c_2{\delta }^{\prime }(x)$ satisfies the generalised function relation $x^{2}g(x)=0$ for $c_1,c_2$ arbitrary constants. Justify your steps fully.

• Learning from the shape of the solution to $x^{2}g=0$ in part 1, what would you propose as the generalised solution to the relation $x^{3}g(x)=0$? and as the generalised solution to the relation $x^{n}g(x)=0$ for $n\in \mathbb{N},n\ge 4$? Give a very brief argument to support your answers.

Exercise 2.8

1. Let $f$ be a function with a unique zero at $x=x_0$ in an open interval $(a,b)$. If this zero is simple (i.e. has multiplicity one) and if $f^{\prime }(x_0)>0$ on the interval, then show that

   $$\mathrm{\Theta }(f(x))=\mathrm{\Theta }(x-x_0),x\in (a,b).$$ (2.1)

   How is this relation modified if instead?

2. Use the relations obtained in part (a) to derive the equality

   $$\delta (f(x))=\frac{1}{|f^{\prime }(x_0)|}\delta (x-x_0).$$ (2.2)

Exercise 2.9

1. Why can one consider the distribution $x\mathrm{\Theta }$ as an antiderivative of the regular distribution $\mathrm{\Theta }$, which is associated with the Heaviside (unit step) function?

2. Using induction, show that

   $$\frac{{\left({(x\mathrm{\Theta })}^k\right)}^{(k+1)}}{k!}=\delta ,k\in \mathbb{N}.$$ (2.3)

Exercise 2.10

Consider the first order differential equation

$${(\sin (x))}^2{T}^{\prime }=0,T\in {𝒟}^{\prime }(ℝ).$$

What is its most general solution in the sense of distributions? Justify your answer fully by proving that your candidate solution satisfies the differential equation in the sense of distributions.

Exercise 2.11

Suppose you wish to solve the following ‘algebraic’ equation for the generalised function $g$,

$$\varphi (x)g(x)=0$$ (2.4)

where $\varphi \mathit{}\mathrm{(}x\mathrm{)}$ is a given smooth function. According to the sifting property of a factor of the delta function (see formula (2.12) in the lecture notes), if $\varphi \mathit{}\mathrm{(}x\mathrm{)}$ vanishes at some point $x_{\mathrm{0}}$, then the generalised function

$$g(x)=K\delta (x-x_0),K\mathrm{constant}$$

satisfies (2.4). Knowing this, can you find the generalised solution $y\mathit{}\mathrm{(}x\mathrm{)}$ of the following equations in terms of $\delta$ and its derivatives?

1. $(x^3+2x^2+x)y(x)=0$

2. $(e^{-x}-1)y(x)=0$

3. $(x^3+2x^2-x-2)y(x)=0$

Exercise 2.12

Determine which of the following are piecewise continuous, piecewise smooth or neither:

1. $f(x)=x$ for $-\pi \le x\le 0$, $f(x)=\pi$ for .

2. $f(x)=\tan x$ for $-\pi \le x\le \pi$.

3. $f(x)=\exp (1/x)$ for and , $f(0)=0$.

4. $f(x)=\sin (1/x)$ for and , $f(0)=0$.

5. $f(x)=x\sin (1/x)$ for and , $f(0)=0$.

Exercise 2.13 (GRAD 2)

Consider the function $f\mathrm{:}\mathrm{[}\mathrm{-}\mathrm{5}\mathrm{,}\mathrm{5}\mathrm{]}\mathrm{\to }\mathrm{R}$ defined as

• Is $f$ piecewise smooth? Justify fully. [3 marks]

• Rewrite $f$ with the help of the unit step function defined as [3 marks]

• Calculate the derivative of $f$ in the sense of distributions. [4 marks]

Exercise 2.14 (GRAD 2)

• Consider the function $f:ℝ\to ℝ:x\mapsto f(x)=x(x^2+3x+2)$ and calculate, for any test function $\psi \in 𝒟(ℝ)$, the integral [4 marks]

  $${\int }_{ℝ}\delta (f(x))\psi (x)𝑑x,$$

  where $\delta \in {𝒟}^{\prime }(ℝ)$ is the Dirac delta distribution.

• Consider the distribution $(x^2-1){\delta }_{(\alpha )}\in {𝒟}^{\prime }(ℝ)$, where ${\delta }_{(\alpha )}$ is the Dirac delta distribution dilated by a factor $\alpha \in ℝ-\{0\}$.

  • For which value of $B$ and $C$ do we have the following equalities of distributions? Justify your answers by integrating both sides against an arbitrary test function $\psi \in 𝒟(ℝ)$.

    • $(x^2-1){\delta }_{(2)}=B\delta$ [2 marks]

    • $(x^2-1){\delta }_{(-2)}=C\delta$ [2 marks]

  • Can you infer a basic identity satisfied by $\delta (x)$ ‘in the sense of distributions’ from the results you obtained in part (i)(1) and part (i)(2)? [2 marks]

3 Unit 3: Sturm-Liouville Theory

Exercise 3.1

Show that the integral

$$⟨u,v⟩:={\int }_0^{\mathrm{\infty }}\overline{u}(x)v(x)e^{-x}𝑑x$$

defines an inner product on the quotient space ${\stackrel{\mathrm{~}}{L}}^{\mathrm{2}}\mathit{}\mathrm{(}\mathrm{[}\mathrm{0}\mathrm{,}\mathrm{\infty }\mathrm{)}\mathrm{)}\mathrm{:=}{L}^{\mathrm{2}}\mathit{}\mathrm{(}\mathrm{[}\mathrm{0}\mathrm{,}\mathrm{\infty }\mathrm{)}\mathrm{)}\mathrm{/}\mathrm{Z}$, where $\mathrm{Z}$ is the set of all square-integrable functions that are non-zero on a set of Lebesgue measure zero, i.e. verify the axioms of a Hermitian inner product, justifying your claims.

Exercise 3.2

Show that the operator $T\mathrm{:}{\mathrm{\ell }}^{\mathrm{2}}\mathrm{\to }{\mathrm{\ell }}^{\mathrm{2}}\mathrm{:}\mathrm{x}\mathrm{\mapsto }T\mathit{}\mathrm{x}$ where $T\mathit{}\mathrm{x}\mathrm{=}\mathrm{(}{x}_{\mathrm{1}}\mathrm{,}{\displaystyle \frac{x_{\mathrm{2}}}{\mathrm{2}}}\mathrm{,}{\displaystyle \frac{x_{\mathrm{3}}}{\mathrm{3}}}\mathrm{,}\mathrm{\dots }\mathrm{)}$ is bounded.

We recall the definition of the space ${\mathrm{\ell }}^{\mathrm{2}}$ below (you should think of $f\mathit{}\mathrm{(}i\mathrm{)}$ as being $x_i$ in this exercise). Definition: Let ${\mathrm{\ell }}^{\mathrm{2}}$ be the subspace of ${\mathrm{C}}^{\mathrm{\infty }}$ of all square-summable sequences, i.e. sequences of type $\mathrm{f}\mathrm{:=}{\mathrm{(}f\mathrm{}\mathrm{(}i\mathrm{)}\mathrm{)}}_{i\mathrm{\in }\mathrm{N}}$, with $f$ a complex-valued function $f\mathrm{:}\mathrm{N}\mathrm{\to }\mathrm{C}\mathrm{:}i\mathrm{\mapsto }f\mathrm{}\mathrm{(}i\mathrm{)}$ and

On that space, the inner product is given by

$$⟨𝐟,𝐠⟩:=\sum _{i=1}^{\mathrm{\infty }}\overline{f(i)}g(i),$$

and the induced norm is given by ${\mathrm{\parallel }\mathrm{f}\mathrm{\parallel }}_{{\mathrm{\ell }}^{\mathrm{2}}}\mathrm{:=}{\mathrm{\left(}{\mathrm{\sum }}_{i\mathrm{=}\mathrm{1}}^{\mathrm{\infty }}{\mathrm{|}f\mathrm{}\mathrm{(}i\mathrm{)}\mathrm{|}}^{\mathrm{2}}\mathrm{\right)}}^{\mathrm{1}\mathrm{/}\mathrm{2}}$.

Exercise 3.3

Convert the following linear second order differential operators into Sturm-Liouville form:

1. $L=x^2{\displaystyle \frac{d^2}{d{x}^2}}+x{\displaystyle \frac{d}{dx}}+2$ for $x>0$.

2. $L=(1-x^2){\displaystyle \frac{d^2}{d{x}^2}}-x{\displaystyle \frac{d}{dx}}+{\nu }^2$ for $\nu$ constant and .

3. $L=(1-x^2){\displaystyle \frac{d^2}{d{x}^2}}-3x{\displaystyle \frac{d}{dx}}+\nu (\nu +2)$ for $\nu$ constant and

4. (TUT 3) $L={\displaystyle \frac{d^2}{d{x}^2}}-2x{(1-x^2)}^{-1}{\displaystyle \frac{d}{dx}}-m^2{(1-x^2)}^{-2}$ for

5. $L=x{\displaystyle \frac{d^2}{d{x}^2}}+(1-x){\displaystyle \frac{d}{dx}}+\nu$ for $\nu$ constant and

6. $L={\displaystyle \frac{d^2}{d{x}^2}}-2x{\displaystyle \frac{d}{dx}}+2\nu$ for $\nu$ constant and $x\in ℝ$

Exercise 3.4

Consider the linear second order differential operator,

with $\mu \mathrm{,}\nu$ non zero real constants.

• Justify why $L$ is not formally self-adjoint.

• Convert $L$ into Sturm-Liouville form.

Exercise 3.5

Consider the Sturm-Liouville operator $\mathrm{L}\mathrm{=}{\displaystyle \frac{d}{d\mathit{}x}}\mathit{}\mathrm{\left(}{p}_{\mathrm{0}}\mathit{}\mathrm{(}x\mathrm{)}\mathit{}{\displaystyle \frac{d}{d\mathit{}x}}\mathrm{\right)}\mathrm{+}{p}_{\mathrm{2}}\mathit{}\mathrm{(}x\mathrm{)}$ with real-valued functions $p_{\mathrm{0}}\mathrm{\in }{\mathrm{C}}^{\mathrm{2}}\mathit{}\mathrm{(}\mathrm{[}a\mathrm{,}b\mathrm{]}\mathrm{)}$ and $p_{\mathrm{2}}\mathrm{\in }\mathrm{C}\mathit{}\mathrm{(}\mathrm{[}a\mathrm{,}b\mathrm{]}\mathrm{)}$.

1. (TUT 3) Which conditions would you put on $p_0$ at the boundaries of the interval $[a,b]$ to ensure that the Sturm-Liouville operator is not just formally self-adjoint, but such that the boundary terms in Green’s formula vanish irrespective of the boundary conditions one might put on the functions $u$ and $v$ acted upon by $𝔏$ in a BVP problem?

2. Using your findings in part $(a)$, determine the ‘natural’ interval $ℐ$ over which each of the following Sturm-Liouville operator is self-adjoint. By ‘natural’, we mean ‘as determined by the boundary conditions on $p_0$’.

   • (TUT 3) $𝔏=(1-x^2){\displaystyle \frac{d^2}{d{x}^2}}-2x{\displaystyle \frac{d}{dx}}-m^2{(1-x^2)}^{-1}$ with $m\in ℝ$

   • $𝔏=x^{m+1}{e}^{-x}{\displaystyle \frac{d^2}{d{x}^2}}+\left((m+1)x^m-x^{m+1}\right)e^{-x}{\displaystyle \frac{d}{dx}}$     for $m\in {ℝ}_{>0}$.

   • $𝔏=e^{-x^2}{\displaystyle \frac{d^2}{d{x}^2}}-2x{e}^{-x^2}{\displaystyle \frac{d}{dx}}$

Exercise 3.6 (TUT 3)

Consider the boundary value problem (BVP) for ,

$$(1+x^2)u^{\prime \prime }+2x{u}^{\prime }+u=1+x,u(0)=1,u(1)=2.$$

Suppose $u$ is a solution to this BVP and write it in the form $u\mathit{}\mathrm{(}x\mathrm{)}\mathrm{=}\mathrm{1}\mathrm{+}x\mathrm{+}v\mathit{}\mathrm{(}x\mathrm{)}\mathrm{.}$ What is the BVP satisfied by $v$? Is it self-adjoint?

Exercise 3.7

Consider the boundary value problem (BVP) for ,

$$x{u}^{\prime \prime }+u^{\prime }+\frac{2}{x}u=e^x,u(1)=2,u(4)=e.$$

Suppose $u$ is a solution to this BVP and write it in the form $u\mathit{}\mathrm{(}x\mathrm{)}\mathrm{=}\frac{\mathrm{2}}{\mathrm{3}}\mathit{}\mathrm{(}\mathrm{4}\mathrm{-}x\mathrm{)}\mathrm{+}\frac{e}{\mathrm{3}}\mathit{}\mathrm{(}x\mathrm{-}\mathrm{1}\mathrm{)}\mathrm{+}v\mathit{}\mathrm{(}x\mathrm{)}\mathrm{.}$ What is the BVP for $v$? Is it self-adjoint?

Exercise 3.8

Revisit exercises 3.6 and 3.7 above and compare the given initial BVP (for $u$) to the BVP (for $v$) that you have obtained in tutorials and in your formative assignment.

• At the light of these two specific examples, and using the same notations for $u$ and $v$, find the general form of the function $g(x):=u(x)-v(x)$ for all $x\in [a,b]$ that will ensure the BVP for $v$ has homogeneous Dirichlet boundary conditions. You may set the initial BVP on $[a,b]$ as

  $$𝔏u=f,u(a)=A,u(b)=B,A,B\in ℝ,$$

  with $𝔏={\displaystyle \frac{d}{dx}}\left(p_0(x){\displaystyle \frac{d}{dx}}\right)+p_2(x)$ a Sturm-Liouville operator and $f$ a source term. You may further assume that all functions are ‘sufficiently well-behaved’.

• Is the BVP for $v$ self-adjoint? Justify.

Exercise 3.9

Consider the Sturm-Liouville operator $\mathrm{L}\mathrm{=}{\displaystyle \frac{d}{d\mathit{}x}}\mathit{}\mathrm{\left(}{p}_{\mathrm{0}}\mathit{}\mathrm{(}x\mathrm{)}\mathit{}{\displaystyle \frac{d}{d\mathit{}x}}\mathrm{\right)}\mathrm{+}{p}_{\mathrm{2}}\mathit{}\mathrm{(}x\mathrm{)}$ acting on functions $u\mathit{}\mathrm{(}x\mathrm{)}$ defined on the interval $\mathrm{[}a\mathrm{,}b\mathrm{]}$. Find adjoint boundary conditions in the following cases. (i) Neumann $u^{\mathrm{\prime }}\mathit{}\mathrm{(}a\mathrm{)}\mathrm{=}{u}^{\mathrm{\prime }}\mathit{}\mathrm{(}b\mathrm{)}\mathrm{=}\mathrm{0}$; (ii) Periodic $u\mathit{}\mathrm{(}a\mathrm{)}\mathrm{=}u\mathit{}\mathrm{(}b\mathrm{)}\mathrm{,}{u}^{\mathrm{\prime }}\mathit{}\mathrm{(}a\mathrm{)}\mathrm{=}{u}^{\mathrm{\prime }}\mathit{}\mathrm{(}b\mathrm{)}$; (iii) Initial $u\mathit{}\mathrm{(}a\mathrm{)}\mathrm{=}{u}^{\mathrm{\prime }}\mathit{}\mathrm{(}a\mathrm{)}\mathrm{=}\mathrm{0}$. Which boundary conditions are self-adjoint? (for part (b), assume that $p_{\mathrm{0}}$ is a nowhere vanishing periodic function on $\mathrm{[}a\mathrm{,}b\mathrm{]}$, i.e. $p_{\mathrm{0}}\mathit{}\mathrm{(}a\mathrm{)}\mathrm{=}{p}_{\mathrm{0}}\mathit{}\mathrm{(}b\mathrm{)}\mathrm{\ne }\mathrm{0}$).

Exercise 3.10

Let

$$𝔏=\frac{d}{dx}\left(p_0(x)\frac{d}{dx}\right)+p_2(x),a\le x\le b$$

be a Sturm-Liouville operator with $p_{\mathrm{0}}\mathrm{\in }{\mathrm{C}}^{\mathrm{2}}\mathit{}\mathrm{(}\mathrm{[}a\mathrm{,}b\mathrm{]}\mathrm{)}$, $p_{\mathrm{0}}\mathit{}\mathrm{(}x\mathrm{)}\mathrm{>}\mathrm{0}$ and $p_{\mathrm{2}}\mathrm{\in }\mathrm{C}\mathit{}\mathrm{(}\mathrm{[}a\mathrm{,}b\mathrm{]}\mathrm{)}$. Consider the BVP ($f$ being a bounded function on $\mathrm{[}a\mathrm{,}b\mathrm{]}$),

$$𝔏u=f,\{\begin{array}{c}\hfill B_1(u)=u(b)+\alpha u(a)+\beta u^{\prime }(a)=0,\hfill \\ \hfill B_2(u)=u^{\prime }(b)+\gamma u(a)+\delta u^{\prime }(a)=0.\hfill \end{array}$$

What are the conditions on the real constants $\alpha \mathrm{,}\beta \mathrm{,}\gamma \mathrm{,}\delta$ for this BVP to be self-adjoint?

Exercise 3.11 (TUT 3)

Let $\mathrm{\Omega }\mathrm{\subset }{\mathrm{R}}^{\mathrm{3}}$ be a smooth bounded region, and define an operator $L$ by

$$Lu:=\mathbf{\nabla }\cdot (p_0\mathbf{\nabla }u)+p_{2}u$$

where $p_{\mathrm{0}}\mathrm{,}{p}_{\mathrm{2}}$ are smooth functions on the closure of $\mathrm{\Omega }$, which we denote $\overline{\mathrm{\Omega }}$. Show that

$${\int }_{\mathrm{\Omega }}u(𝐱)Lv(𝐱)𝑑𝐱={\int }_{\mathrm{\Omega }}v(𝐱)Lu(𝐱)𝑑𝐱$$

for all functions $u\mathrm{,}v\mathrm{:}\mathrm{\Omega }\mathrm{\to }\mathrm{R}$ that vanish on the boundary $\mathrm{\partial }\mathit{}\mathrm{\Omega }$ of $\mathrm{\Omega }$.

Exercise 3.12 (TUT 4)

Consider the regular Sturm-Liouville eigenvalue problem on $\mathrm{[}a\mathrm{,}b\mathrm{]}$

$𝔏u(x)+\lambda u(x)=0,$

$B_1(u):={\alpha }_{1}u(a)+{\beta }_1{u}^{\prime }(a)=0,$ $B_2(u):={\eta }_{2}u(b)+{\kappa }_2{u}^{\prime }(b)=0,$ (3.1)

with $\mathrm{L}\mathrm{=}\frac{d}{d\mathit{}x}\mathit{}\mathrm{\left(}{p}_{\mathrm{0}}\mathit{}\mathrm{(}x\mathrm{)}\mathit{}\frac{d}{d\mathit{}x}\mathrm{\right)}\mathrm{+}{p}_{\mathrm{2}}\mathit{}\mathrm{(}x\mathrm{)}$ where $p_{\mathrm{0}}$ and $p_{\mathrm{2}}$ are real-valued functions and $p_{\mathrm{0}}\mathrm{>}\mathrm{0}$ on $\mathrm{[}a\mathrm{,}b\mathrm{]}$. Show that if $p_{\mathrm{2}}\mathit{}\mathrm{(}x\mathrm{)}\mathrm{\le }\mathrm{0}$ for all $x\mathrm{\in }\mathrm{[}a\mathrm{,}b\mathrm{]}$, and if ${\alpha }_{\mathrm{1}}\mathit{}{\beta }_{\mathrm{1}}\mathrm{\le }\mathrm{0}$ and ${\eta }_{\mathrm{2}}\mathit{}{\kappa }_{\mathrm{2}}\mathrm{\ge }\mathrm{0}$, then all eigenvalues ${\lambda }_n\mathrm{\ge }\mathrm{0}$.

Exercise 3.13

Consider the Sturm-Liouville equation

$$𝔏u(x)+\lambda u(x)=0,𝔏:=\frac{d}{dx}\left(p_0(x)\frac{d}{dx}\right)+p_2(x),\lambda \mathrm{real}\mathrm{constant},$$

with $p_{\mathrm{0}}\mathrm{\in }{\mathrm{C}}^{\mathrm{2}}\mathit{}\mathrm{(}\mathrm{[}a\mathrm{,}b\mathrm{]}\mathrm{)}$ and $p_{\mathrm{2}}\mathrm{\in }\mathrm{C}\mathit{}\mathrm{(}\mathrm{[}a\mathrm{,}b\mathrm{]}\mathrm{)}$ two real-valued functions.
If $u_{\mathrm{1}}$ and $u_{\mathrm{2}}$ are two distinct solutions of the Sturm-Liouville equation, show that

$$p_0(x)(u_1(x)u_2^{\prime }(x)-u_2(x)u_1^{\prime }(x))$$

is a constant.

Exercise 3.14 (GRAD 3)

Consider the Sturm-Liouville eigenvalue problem on $\mathrm{[}\mathrm{1}\mathrm{,}b\mathrm{]}$ for $b\mathrm{>}\mathrm{1}$,

$${(x^2{y}^{\prime })}^{\prime }+\lambda y=0,y(1)=y(b)=0.$$

Find the eigenvalues and the normalised eigenfunctions of the problem.
(Hint: In the course of solving this problem, you will encounter a differential equation of the Cauchy-Euler type, i.e. of the form

$$x^2{y}^{\prime \prime }(x)+ax{y}^{\prime }(x)+by(x)=0,a,b\mathrm{real}\mathrm{constants}.$$

To solve it, set $x\mathrm{=}{e}^t$ to obtain a differential equation with constant coefficients in the variable $v\mathit{}\mathrm{(}t\mathrm{)}\mathrm{:=}y\mathit{}\mathrm{(}{e}^t\mathrm{)}$.)

Exercise 3.15

Consider the Sturm-Liouville eigenvalue problem on $\mathrm{[}\mathrm{0}\mathrm{,}\pi \mathrm{]}$ given by,

Find the eigenvalues and the normalised eigenfunctions (assume $\lambda \mathrm{>}\mathrm{4}$).

Exercise 3.16

Consider the BVP on $\mathrm{[}\mathrm{1}\mathrm{,}\mathrm{2}\mathrm{]}$ given by

$$x^2{u}^{\prime \prime }+x{u}^{\prime }+(\lambda +2)u=0,u^{\prime }(1)=0,u^{\prime }(2)=0,\lambda \mathrm{real}\mathrm{constant}.$$

1. Identify the Sturm-Liouville operator $𝔏$ and the weight $\omega (x)$ when the differential equation appearing in the BVP is rewritten as the eigenvalue equation $𝔏u(x)+(\lambda +2)\omega (x)u(x)=0$.

2. Find the eigenvalues and the normalised eigenfunctions of the SL eigenvalue problem

   $$𝔏u+(\lambda +2)\omega u=0,u^{\prime }(1)=0,u^{\prime }(2)=0,\lambda \ge -2.$$

Exercise 3.17 (GRAD 3)

1. Write the differential equation

   $$Lu(x):=x{u}^{\prime \prime }(x)+(2-x)u^{\prime }(x)+\nu u(x)=0,\nu \mathrm{real}\mathrm{constant},$$

   in Sturm-Liouville form, i.e. identify the Sturm-Liouville operator $\widetilde{𝔏}$, the weight $\omega (x)$ and the parameter $\lambda$ when $Lu(x)=0$ is rewritten in the form $\widetilde{𝔏}u(x)+\lambda \omega (x)u(x)=0$.

2. What is the natural interval of definition for this Sturm-Liouville eigenvalue equation?

3. The eigenfunctions $u_n(x)$ of this Sturm-Liouville problem associated with the eigenvalues ${\lambda }_n=n$ are given by

   $$u_n(x)=\frac{e^x}{xn!}\frac{d^n}{d{x}^n}\left(x^{n+1}{e}^{-x}\right),n\in \mathbb{N}\cup \{0\}.$$

   Distinct eigenfunctions are mutually orthogonal w.r.t. the inner product ${⟨\cdot ,\cdot ⟩}_{\omega }$. Check this statement for $u_1$ and $u_2$. (You may use the result ${\int }_0^{\mathrm{\infty }}{x}^k{e}^{-x}𝑑x=k!$ for $k\in \mathbb{N}$)

Exercise 3.18

Consider the Sturm-Liouville eigenvalue problem on $\mathrm{[}\mathrm{0}\mathrm{,}\mathrm{1}\mathrm{]}$,

Find the eigenvalues ${\lambda }_n$ of this problem, and obtain the corresponding normalised eigenfunctions ${\widehat{u}}_n\mathit{}\mathrm{(}x\mathrm{)}$.

Exercise 3.19 (TUT 4)

Consider the following Sturm-Liouville problem on $\mathrm{[}\mathrm{0}\mathrm{,}\mathrm{1}\mathrm{]}$

1. Show that all the eigenvalues are positive.

2. Solve the problem.

Exercise 3.20

Use the method of eigenfunctions expansion to solve the inhomogeneous problem on $\mathrm{[}\mathrm{0}\mathrm{,}\mathrm{1}\mathrm{]}$ given by

Exercise 3.21 (TUT 4)

Solve the following BVP problem on $\mathrm{[}\mathrm{0}\mathrm{,}\pi \mathrm{]}$

using an eigenfunction expansion.

Exercise 3.22 (TUT 4)

Construct the generalised Fourier series expansion $F_f\mathit{}\mathrm{(}x\mathrm{)}\mathrm{:=}{\mathrm{\sum }}_{n\mathrm{=}\mathrm{1}}^{\mathrm{\infty }}{f}_n\mathit{}{\widehat{u}}_n\mathit{}\mathrm{(}x\mathrm{)}$ for the function

where the set ${\mathrm{\{}{\widehat{u}}_n\mathrm{\}}}_{n\mathrm{\in }\mathrm{N}}$ is the set of orthonormal eigenfunctions ${\widehat{u}}_n\mathit{}\mathrm{(}x\mathrm{)}\mathrm{=}\sqrt{\frac{\mathrm{2}}{\pi }}\mathit{}\cos \mathit{}\mathrm{\left(}\mathrm{(}n\mathrm{-}\frac{\mathrm{1}}{\mathrm{2}}\mathrm{)}\mathit{}\pi \mathit{}x\mathrm{\right)}$ stemming from a Sturm-Liouville eigenvalue problem on the interval $\mathrm{[}\mathrm{0}\mathrm{,}\mathrm{1}\mathrm{]}$ with weight $\omega \mathit{}\mathrm{(}x\mathrm{)}\mathrm{=}\mathrm{1}$. Calculate $F_f\mathit{}\mathrm{(}\frac{\mathrm{1}}{\mathrm{4}}\mathrm{)}\mathrm{,}{F}_f\mathit{}\mathrm{(}\frac{\mathrm{1}}{\mathrm{2}}\mathrm{)}$ and $F_f\mathit{}\mathrm{(}\frac{\mathrm{3}}{\mathrm{4}}\mathrm{)}$ and compare with $f\mathit{}\mathrm{(}\frac{\mathrm{1}}{\mathrm{4}}\mathrm{)}\mathrm{,}f\mathit{}\mathrm{(}\frac{\mathrm{1}}{\mathrm{2}}\mathrm{)}$ and $f\mathit{}\mathrm{(}\frac{\mathrm{3}}{\mathrm{4}}\mathrm{)}$.

4 Unit 4 Green’s functions

4.1 Green’s functions for ODEs

Exercise 4.1 (GRAD 4)

Solve the forced oscillator problem on $\mathrm{[}\mathrm{0}\mathrm{,}\mathrm{\infty }\mathrm{)}$ using the ‘first shade of Green’:

$$\frac{d^{2}x(t)}{d{t}^2}+x(t)=2\cos t,x(0)=4,{\frac{dx(t)}{dt}|}_{t=0}=0.$$

All steps of the method used must be worked out in detail.

Exercise 4.2

The equation of motion for a driven damped harmonic oscillator can be written

$$\ddot{x}+2\dot{x}+(1+{\kappa }^2)x=f(t)$$

with $\kappa \mathrm{\ne }\mathrm{0}$. If it starts from rest with $x\mathit{}\mathrm{(}\mathrm{0}\mathrm{)}\mathrm{=}\mathrm{0}$ and $\dot{x}\mathit{}\mathrm{(}\mathrm{0}\mathrm{)}\mathrm{=}\mathrm{0}$,

1. find the corresponding Green’s function $G(t,\tau )$ and verify that it can be written as a function of $t-\tau$ only.

2. find the explicit solution when the driving force is the unit step function, i.e.

Exercise 4.3 (TUT 5)

Consider the Green’s function defined on $\mathrm{0}\mathrm{\le }x\mathrm{\le }\pi$, $\mathrm{0}\mathrm{\le }\xi \mathrm{\le }\pi$,

1. Show that the function $u(x)$ defined by

   $$u(x)={\int }_0^{\pi }G(x,\xi )f(\xi )𝑑\xi$$

   satisfies the equation ${\displaystyle \frac{d^{2}u}{d{x}^2}}+u=f$, where $f$ can be an arbitrary continuous function.

2. Show that $u(0)=u^{\prime }(\pi )=0$ for any $f$, but that $u(\pi )$ depends on the form of $f$.

Exercise 4.4

Show that the Green’s function

is symmetric in the exchange of $x$ and $\xi$ whenever the BVP on $\mathrm{[}a\mathrm{,}b\mathrm{]}$ is given by $L\mathit{}u\mathit{}\mathrm{(}x\mathrm{)}\mathrm{=}f\mathit{}\mathrm{(}x\mathrm{)}\mathrm{,}{B}_{\mathrm{1}}\mathit{}\mathrm{(}u\mathrm{)}\mathrm{=}\mathrm{0}\mathrm{=}{B}_{\mathrm{2}}\mathit{}\mathrm{(}u\mathrm{)}$ for a self-adjoint differential operator $L\mathrm{=}{p}_{\mathrm{0}}\mathit{}\frac{d^{\mathrm{2}}}{d\mathit{}{x}^{\mathrm{2}}}\mathrm{+}{p}_{\mathrm{0}}^{\mathrm{\prime }}\mathit{}\frac{d}{d\mathit{}x}\mathrm{+}{p}_{\mathrm{2}}$.

Exercise 4.5

Solve the following IN/HOM BVP on $\mathrm{0}\mathrm{\le }x\mathrm{\le }\frac{\pi }{\mathrm{2}}$,

$$\frac{d^{2}u}{d{x}^2}+u=\mathrm{cosec}x,u(0)=u(\frac{\pi }{2})=0,$$

by first calculating the relevant Green’s function.

Exercise 4.6

Find the Green’s function satisfying

$$\frac{{\partial }^{2}G(x,\xi )}{\partial x^2}-G(x,\xi )=\delta (x-\xi ),G(0,\xi )=G(1,\xi )=0.$$

Exercise 4.7 (TUT 5)

Solve the BVP

$$-y^{\prime \prime }(x)-y(x)=f(x),y(0)=0,y(1)=1$$

for $x\mathrm{\in }\mathrm{[}\mathrm{0}\mathrm{,}\mathrm{1}\mathrm{]}$ using Green’s functions.

Exercise 4.8 (TUT 5)

Consider again the BVP on $\mathrm{[}\mathrm{0}\mathrm{,}\mathrm{1}\mathrm{]}$ of the previous exercise, namely

$$-y^{\prime \prime }(x)-y(x)=f(x),y(0)=0,y(1)=1.$$

Let ${\stackrel{\mathrm{~}}{y}}_{\mathrm{1}}\mathit{}\mathrm{(}x\mathrm{)}$ and ${\stackrel{\mathrm{~}}{y}}_{\mathrm{2}}\mathit{}\mathrm{(}x\mathrm{)}$ be two linearly independent solutions of the homogeneous differential equation associated with the given BVP, i.e. solutions of $\mathrm{-}{y}^{\mathrm{\prime \prime }}\mathrm{-}y\mathrm{=}\mathrm{0}$, with boundary conditions ${\stackrel{\mathrm{~}}{y}}_{\mathrm{1}}\mathit{}\mathrm{(}\mathrm{0}\mathrm{)}\mathrm{=}\mathrm{0}$ and ${\stackrel{\mathrm{~}}{y}}_{\mathrm{2}}\mathit{}\mathrm{(}\mathrm{1}\mathrm{)}\mathrm{=}\mathrm{0}$.

Show that the function $\stackrel{\mathrm{~}}{G}\mathit{}\mathrm{(}x\mathrm{,}\xi \mathrm{)}$ defined as

yields the Green’s function found in Exercise 4.7.

4.2 Green’s functions for PDEs

Exercise 4.9

Fix the point $𝛏\mathrm{=}\mathrm{(}{𝛏}_{\mathrm{1}}\mathrm{,}{𝛏}_{\mathrm{2}}\mathrm{)}$ in the plane and check that the function

$$G_2(𝐱,𝝃):=-\frac{1}{2\pi }\ln \frac{1}{r},$$

where $r\mathrm{:=}\mathrm{|}\mathrm{x}\mathrm{-}𝛏\mathrm{|}$ is the distance between $\mathrm{x}$ and $𝛏$ is a solution to the problem

$${\nabla }^{2}u(𝐱)=\frac{d^{2}u(𝐱)}{d{x}_1^2}+\frac{d^{2}u(𝐱)}{d{x}_2^2}=0$$

except at $\mathrm{x}\mathrm{=}𝛏$.

Exercise 4.10

Method of images

1. Construct the Green’s function $G(𝐱,{𝝃}_0)$ for the Dirichlet Poisson problem

   $${\mathbf{\nabla }}^{2}u(𝐱)=f(𝐱),u(𝐱)|{}_{\partial \mathrm{\Omega }}=g(𝐱),$$

   where the wedge domain has boundary $\partial \mathrm{\Omega }=\{y=0,x\ge 0\}\cup \{(x,y)\in {ℝ}^2:x=y,x>0\}$.
   

2. Show by a direct calculation using what you found for $G_{\mathrm{reg}}$ that ${\mathbf{\nabla }}_{𝐱}^2{G}_{\mathrm{reg}}(𝐱,{𝝃}_0)=0$, where $G_{\mathrm{reg}}=G_2-G$, with $G_2$ the fundamental solution to Laplace’s equation in two dimensions.

3. Check that on the boundary, $G_2=G_{\mathrm{reg}}$.

Exercise 4.11

Method of images
A line charge in the $z$-direction, of charge density $\rho$, is placed at some position $𝛏$ in the quarter space $\mathrm{\{}x\mathrm{>}\mathrm{0}\mathrm{,}y\mathrm{>}\mathrm{0}\mathrm{\}}$. Calculate the force per unit length on the line charge due to the presence of thin earthed plates along $x\mathrm{=}\mathrm{0}$ and $y\mathrm{=}\mathrm{0}$.
Hint: The force per unit length on the line charge with charge density $\rho$ at position $𝝃$ due to charges in the neighbourhood is $𝐅=-\rho \mathbf{\nabla }u(𝐱)|{}_{𝐱=𝝃}$, where the potential $u$ is the solution to Poisson’s equation (with ${ϵ}_0$ constant)

$${\mathbf{\nabla }}^{2}u(𝐱)=\frac{\rho }{{ϵ}_0}\delta (𝐱-𝝃)$$ (4.1)

in the quarter plane $\mathrm{\Omega }=\{x>0,y>0\}$, with Dirichlet boundary conditions $u(0,y)=u(x,0)=0$. To solve this problem, proceed in four steps

1. Construct the Green’s function $G(𝐱,𝝃)$ by the method of images, with the fundamental solution taken to be $G_2(𝐱,𝝃)$ (see lecture notes). Draw a picture to help your reasoning.

2. Check that the Green’s function you found is zero on the boundary $\partial \mathrm{\Omega }$ and when $|𝐱|\to \mathrm{\infty }$

3. Express the potential $u(𝐱)$ satisfying (4.1) in terms of the Green’s function $G(𝐱,𝝃)$

4. Calculate the force $𝐅(𝐱)$ experienced by the line charge at $𝝃$ due to the presence of the image line charges of charge density $\pm \rho$.

Exercise 4.12

Method of images

Find the Green’s function for the Poisson Dirichlet problem ${\mathrm{\nabla }}^{\mathrm{2}}\mathit{}u\mathit{}\mathrm{(}\mathrm{x}\mathrm{)}\mathrm{=}f\mathit{}\mathrm{(}\mathrm{x}\mathrm{)}$ on , with $u\mathit{}\mathrm{(}\mathrm{x}\mathrm{)}\mathrm{=}g\mathit{}\mathrm{(}\mathrm{x}\mathrm{)}$ when $\mathrm{|}\mathrm{x}\mathrm{|}\mathrm{=}\mathrm{R}$ and 0 otherwise.

Exercise 4.13 (extension)

Find the Poisson kernel for the Poisson Dirichlet problem of the previous question.